Abstract
Background
Chromosomal DNA replication in bacteria starts at the origin (ori) and the two replicores propagate in opposite directions up to the terminus (ter) region. We hypothesize that the two replicores need to reach ter at the same time to maintain a physical balance; DNA insertion would disrupt such a balance, requiring chromosomal rearrangements to restore the balance. To test this hypothesis, we needed to demonstrate that ori and ter are in a physical balance in bacterial chromosomes. Using wavelet analysis, we documented GC skew, AT skew, purine excess and keto excess on the published bacterial genomic sequences to locate the turning (minimum and maximum) points on the curves. Previously, the minimum point had been supposed to correlate with ori and the maximum to correlate with ter.
Results
We observed a strong tendency of the bacterial chromosomes towards a physical balance, with the minima and maxima corresponding to the known or putative ori and ter and being about half chromosome separated in most of the bacteria studied. A nonparametric method based on wavelet transformation was employed to perform significance tests for the predicted loci.
Conclusions
The wavelet approach can reliably predict the ori and ter regions and the bacterial chromosomes have a strong tendency towards a physical balance between ori and ter.
Similar content being viewed by others
Background
Replication of the bacterial chromosomal DNA starts at the origin (ori) and the two replication forks (or replicores) propagate in opposite directions up to the terminus (ter) region, as demonstrated in Escherichia coli [1–7]. Obviously, the two replication forks need to reach the ter region at the same time to optimize the replication process. It is therefore reasonable to assume that ori and ter should have a physical balance between them, i.e., opposite to each other, on the chromosome to guarantee a synchronous completion of the bi-directional chromosomal replication. Based on this assumption, we hypothesize that lateral transfer of large blocks of DNA into a bacterial chromosome would disrupt such a balance, making necessary the rearrangements of the chromosome to restore the balance. We have observed and reported the large insertions and the striking chromosomal rearrangements in Salmonella typhi [8–10]. The 180° physical balance between ori and ter has been seen in the complete sequence of Escherichia coli K12 [11] and a number of other bacteria sequenced subsequently. To address the importance of such a physical balance of the bacterial chromosomes in evolution, we proposed a model of bacterial speciation, i.e., the Adopt-Adapt Model [12, 13]. However, some sequenced chromosomes, such as that of Bacillus subtilis [14], show significant deviation of ori and ter from the hypothesized 180° relationship. Additionally, in many of the sequenced bacterial chromosomes, the locations of ori and ter are not reported. In order to know whether a physical balance actually exists in, or is required for the stability of, the bacterial chromosome, we attempted to locate ori and ter in the chromosomes of the sequenced bacteria and then investigate their physical relationships.
One key difficulty in locating ori and ter is that bacterial ori and ter seem not to have conserved nucleotide sequences across different bacteria. However, some chromosomal features, including those that have resulted from asymmetric error rates of replication between the leading and lagging DNA strands [15] such as GC skew and oligomer skews, have proven useful to help in locating the ori and ter regions. Lobry observed that GC skew, i.e., G-C/G+C averaged over a sliding window, changes sign at the origin [16–18]. For the past few years, GC skew (GCS) and AT skew (A-T/A+T averaged over a sliding window, ATS) have been widely used in predicting the ori and ter sites in bacteria [11, 19–21] and viruses [22]. The advantage of GCS and ATS is that they show the turning points clearly. However, the shape of curves and the accuracy of the predicted sites by the conventional GCS analysis methods [16, 17]. are dependent on the window size: the larger the window, the less accurate the sites. Thus, for genomic analysis, the windowed indices may lead to the loss of some critical information.
Oligomer skew analysis, another sequence-based method that finds short oligomers highly skewed on opposite strands of the chromosome, overcomes the window problem [23]. Using this method, Salzberg and colleagues located origins of replication in all 10 bacterial and one of three archaeal genomes analyzed. In some of the bacterial genomes, such as Bacillus subtilis, E. coli, Borrelia burgdorferi, and Mycoplasma genitalium, large numbers of different oligomers showed a significant skew. Although these oligomers locate origin of replication at different sites, varying from 3823 kb to 4002 kb in E. coli K12, for example, combining method could bring the results from multiple oligomers together and locate the origin at a site that is very close to the experimentally determined origin of replication. Unfortunately, different bacteria may have vastly different numbers of skewed oligomers, with some having no detectable skew. Therefore, alternative chromosomal features would be desirable.
Freeman et al. [24] reported three integral functions: purine excess, keto excess and coding-strand excess, and used these three indices to detect the pattern of chromosomal organization in E. coli, H. influenzae, M. genitalium and Synechocystis. In every case where independent information is available, the minimum point in the purine excess curve corresponds to the ori site, and the maximum point of the excess curves correlates with the known or suspected ter site; the keto excess curve reflects the same correlation. The coding-strand excess has the same tendency but shows a more variable behavior compared to the keto and purine excesses (i.e., less unambiguous than the keto and purine excesses in such studies). The main advantage of these indices is that, as with oligomer skews, there are no window slides; in addition, because of their universal existence in bacterial genomes, these indices are at least complementary to the oligomer skew method in locating bacterial ori and ter sites. However, one problem remains: the curves are not sufficiently sharp and smooth, making it difficult to pinpoint the predicted loci and estimate the confidence intervals with significance tests on the statistics. Additionally, although significance tests are usually performed by the t or the χ2 methods, both of these tests are based on the assumption of a normal distribution, while in fact the distributions of the four bases on the bacterial chromosome are neither normal nor uniform.
To address these issues and overcome all of these disadvantages, we assessed the use of wavelet transformation analysis [25], a non-parametric method, to locate the bacterial chromosomal ori and ter sites. This technique was introduced in DNA sequence analysis by A. Arneodo and his group in 1995 [26]. The basic idea of wavelet analysis is to decompose a sequence profile into several groups of coefficients, each group containing information about features of the profile at a different scale. Coefficients at coarse scales capture gross and global features and coefficients at fine scales reveal the local details of the profile. These features of wavelet analysis are ideal for genomic analysis. As one application, wavelet analysis has been used on the G+C patterns occurring in genomes [27–29]. More recently, this technique has also been shown to be very successful in extracting quantitative information on the structure and dynamics of the nucleosomes [30]. Unfortunately most studies using wavelet analysis did not perform statistical significance tests. In this study, we used wavelet transform to locate ori and ter by documenting GC skew, AT skew, keto excess, and purine excess on published bacterial chromosomes and performed statistical significance tests. We observed a strong tendency of the bacterial chromosomes towards a physical balance, with the minima and maxima corresponding to the known or putative ori and ter and being about half chromosome separated in most of the bacteria studied.
Results
Simulation of the wavelet transformation analysis
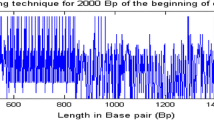
We first tested the wavelet transformation analysis by documenting the chromosome of S. typhimurium LT2 for GC and AT skews (Figure 1) and keto and purine excesses (Figure 2). As shown in Figures 1 and 2, the maximum and minimum points can be very clearly identified by all of these indices except AT skew (See below for more details). The wavelet power spectrum is shown in Figure 3, where the wavelet transformation resulted in a surface, with a contour plot and a squared modulus on a log-scale; the maxima curves and the confidence interval at 95% level were traced out. We then performed Monte-Carlo simulations for 1000 runs to examine and calibrate the performance of the wavelet estimator and to establish the validity of the wavelet estimator. As shown in Figure 4, the wavelet estimator was unbiased: the exact location of the first maximum was 0.30884, the mean estimate of the simulation was 0.30872, and the estimated standard deviation was 0.00162; the exact location of the second maximum was 0.78308, the simulated estimate was 0.78309, and the estimated standard deviation was 0.00181. The wavelet estimator used these distributions to provide confidence intervals on the original signals for localizing the ori and ter sites.
Cumulative diagram analysis
Altogether, we analyzed 36 bacterial chromosomes by wavelet for the four indices (AT and GC skews, and keto and purine excesses). As shown in Table 1, the minima and maxima of these indices (only keto and purine excesses are given in Table 1) coincided with known or putative ori and ter, respectively, and divided the chromosome into approximately equal halves in most of the bacterial sequences analyzed, with rare exceptions (See below). These indices behaved differently in different bacteria: in a given bacterial chromosome, either or both of keto excess and purine excess may show the minima and maxima clearly ("strong" in Table 1) or not clearly ("weak" in Table 1). For example, in E. coli K12, both keto excess and purine excess gave "strong" results (Figure 5); in Borrelia burgdorferi, which was included in this study as a representative of bacteria with linear chromosomes, there was strong keto excess but week purine excess (Figure 6); and in Lactoccocus lactis, there was strong purine excess but week keto excess (Figure 7). A similar situation was seen with GC and AT skews (see Figures 1 &2, where GC skew is strong but AT skew is weak). The four indices, when strong, gave maxima and minima at approximately the same but slightly different chromosomal locations, a similar situation as seen with different oligomers [23]. In Table 1, either keto or purine excess data, whichever were strong, were used; when both were strong, the keto excess data were arbitrarily chosen. Here again, purine/keto excess was used in Table 1 because no window would be involved, whereas GC/AT skew is a derivative function of the base composition of adjacent windows along the chromosome, which reduces the resolution of the analysis. It is important to note that, although the predicted positions for ori and ter are given in Table 1 at a single base resolution, they are not necessarily the true positions of ori and ter – they are the turning points of the skews or excesses and different skews or excesses have different chromosomal locations of their turning points, which are however to different degrees all close to ori or ter (See below and Figures 8 &9).
Expanding of chromosomal regions by wavelet for local features
The most outstanding advantage of the wavelet approach is that it can reveal details of a chromosomal region at any desired resolution, from a coarse scale for a general view of the whole chromosome to fine scales down to single base patterns for local features. In Figure 8, the minimum region of the curve for keto excess in Figure 5 was expanded, where the experimentally determined oriC is shown at a fairly sharp point, co-residing with the minimum of the curve. Figure 9, which is a further expansion of Figure 8, shows the position oriC and its relation in space with the minimum of the curve at the single base resolution. Once curves like the one shown in Figure 4a are created, any part of the whole chromosome can be expanded to a single base resolution promptly, although it is worth mentioning that the non-wavelet skew or purine/keto excess plots can also reach a resolution of a single base or a few bases for a short DNA fragment.
Deviation of the maxima of the four indices from the ter region in the two E. coli O157:H7 strains
The two E. coli O157:H7 strains have superficially very unbalanced chromosomes, with oriC-terC 120° clockwise in EDL933, and oriC-terC 144° clockwise in Sakai-VT2. Are the chromosomes in the two strains really unbalanced? Our results of all four indices obtained by wavelet analyses showed significant deviation of the maxima of the four indices from the ter region but close proximity to tus, and the maxima and minima nevertheless still divided the chromosomes into approximately equal halves (Figure 10), suggesting that these chromosomes are balanced in terms of the actual replication process.
Discussion
Using wavelet analysis, we evaluated the relevance of GC and AT skews and keto and purine excesses with the regions that correspond to replication origin, ori, and terminus, ter. Mechanisms, by which compositional biases are created, are complex and beyond the scope of this work; excellent reviews are available such as that by Frank and Lobry [31]. In this study, our objectives are to find further support to our physical balance hypothesis of the bacterial chromosomes by documenting the compositional biases with wavelet. As shown in the Results, in the cases where ori and ter are reported, the minima and maxima of the curves for the GC and AT skews and keto and purine excesses fall into the regions of ori and ter, respectively. We therefore assumed that the four indices would locate ori and ter also in the cases where ori and ter have not been experimentally determined. The four indices behaved differently, with some being strong and others being weak in different bacteria (Table 1). This may reflect different evolutionary forces affecting GC and AT skews differentially and, essentially, purine excess is equivalent to the sum of GC and AT skews and keto excess to their subtraction [32]. Supporting the Adopt-Adapt model [12, 13], our results show an obvious tendency of the bacterial chromosomes towards a physical balance between ori and ter (Table 1). However, there seemed to be some exceptions among the bacteria analyzed, such as Mycoplasma gentalium (Table 1), where the minimum and maximum of the curve are significantly off the predicted balanced positions (202 degrees vs 180 degrees with a range of plus or minus 15 degrees in all other bacteria listed in Table 1). We need to further clarify the situations in such cases to know whether a chromosomal balance does exist in these bacteria but will have to be revealed in a different way, or whether these bacteria, as intracellular parasites, would have undiscovered mechanisms to compensate for such imbalance.
Characterizations of ori and ter have been performed on very few bacteria so far, therefore very little is known about the common features of these chromosomal loci, especially the ter region. The most detailed information about ori and ter comes from Hill et al. on E. coli K12 [2, 3], who described the terminus region of the E. coli chromosome as being directly opposite to the origin of replication and containing two sites that inhibit the progression of the replication forks. These two sites, T1 and T2, are separated by a 352 kb DNA segment and are located at the two extremities of the terminus region. They also demonstrate that a trans-acting factor encoded by tus is required for replication fork inhibition at both T1 and T2 [3]. In addition, Hill et al. identified a 23 bp sequence common to the region containing T1 and T2, which is sufficient to signal replication fork inhibition in a ColE1-derrived plasmid, and the terminator signal sequence is dependent on its orientation in the plasmid and the presence of the trans-acting termination factor Tus. These findings indicate that the terminus site of DNA replication is a special region, extending for several hundred kb and including loci such as T1, T2, tus, etc. We searched for the positions of the 23 bp signal sequence in all analyzed genome sequences and found unequal numbers in E. coli and Salmonella strains, which were all very close to tus (data not shown). Therefore, it is rather surprising to find that the ter region in E. coli O157:H7 EDL933 (terA through terF, nucleotide positions 1101244 to 1105943) is so far away from tus (nucleotide positions 2359317 to 2360276) or from the supposedly balanced position. The situation is similar with the other sequenced E. coli O157:H7 strain, Sakai-VT2. This unexpected finding raises the question: should the chromosomal balance be between ori and ter (E. coli K12) or between ori and a newly created "ad hoc terminus" (E. coli O157:H7; does the "ad hoc terminus" exist and what is in it)? Our results in Figure 6 strongly suggest that chromosomal replication is symmetrical, i.e., a tendency towards a physical balance exists even when major genomic events may significantly displace the ori or ter region. Perna et al. [33] identified a very large insertion at the terminus region. This insert is likely due to a recent lateral gene transfer, which obviously would disrupt the physical balance of chromosomal replication, as indicated by the relative locations of ori and ter on the genomes of the E. coli O157:H7 strains, and also unbalance the GC/AT skew or purine/keto excess. Over time, this unbalanced skew or excess will probably balance itself out through a process known as amelioration, which has been described in detail by Lawrence and Ochman [34]. Results presented in Figure 10 show that the purine/keto excess could be rebalanced prior to the rebalancing of ori or ter. One important implication here is that termination of DNA replication is occurring in a new chromosomal region that is ca. 180° away from ori, not the annotated ter region. In this sense, the actual physical balance of the bacterial chromosome may be better revealed by the purine/keto excess than by the chromosomal location of ter in relation to ori. The features of the "ad hoc terminus" regions need to be further explored.
From Table 1, it is interesting to note that related bacteria have the same tendency of having strong or weak keto and purine excesses. This may reflect their common evolutionary history and may serve as useful chromosomal features for comparative studies. We also tried wavelet analysis on Archaea; however, none of the four indices was "strong" enough to reveal any minima or maxima that may possibly correspond to ori or ter (data not shown). This finding reflects fundamental differences between Bacteria and Archaea in their chromosomal composition and evolutionary routes.
In this study, we used wavelet transformation analysis for significance test of the predicted loci. Two methods are commonly used in signal data processing, Fourier transformation and wavelet transform analysis. Compared to wavelet analysis, the windowed Fourier transformation suffers from three major defects: (1) the shape of the curve is highly dependent on the window size; (2) in computing the Fourier transform each time using only the data within the window, the window Fourier transform (WFT) gives inconsistent treatment of different frequencies; and (3) the WFT relies on the assumption that the index signal can be decomposed into sinusoidal components. The wavelet method can avoid these defects by decomposing the series in scale and frequency simultaneously. Because of the unknown and uncertain distribution of the indices, for revealing chromosomal features one cannot do significance tests based on conventional statistical methods. Monte-Carlo simulations combined with wavelet analysis supply a useful tool to overcome these issues. The wavelet transformation analysis is particularly suitable for visualizing chromosomal patterns at all scales, from coarse to fine. For example, one might like to separate the shorter period fluctuations from the longer sequences, wavelet analysis will do this, regardless of whether the fluctuation repeats on a regular basis or otherwise. Overall, wavelet is providing a powerful tool for comparative genomics.
Conclusions
Wavelet analysis provides a powerful tool to predict ori and ter on bacterial chromosomes and has revealed a strong tendency of the bacterial chromosomes towards a physical balance between ori and ter.
Methods
Bacterial genome sequences and equipment for wavelet analysis
Bacterial genome sequences analyzed in this study were downloaded from the NCBI website (http://www.ncbi.nlm.nih.gov; Table 1). If we produced the curves for the four indices (GC skew, AT skew, keto excess and purine excess; see below) from the downloaded sequences directly, most of the diagrams would be of the "V" or reverse "V" shape, making the positions for ori and ter obscure (e.g., Bacillus halodurans C-125, Bacillus subtilis, Borrelia burgdorferi, etc). The particular shape depends on the point chosen to initiate the cumulative summation (i.e. the point corresponding to i = 1 in the formulae for the various indices). If this point happens to be too close to either ori or ter, the curve will give an ambiguous estimate of the location of that site. In such cases, we simply chose to start the summation from a different base in the sequence, so that the peak and valley (corresponding to the ori and ter regions) can be clearly identified. The particular starting base for the analysis in each bacterial chromosome is available from the authors on request.
We used wavelet transform methods [27, 28]. in the analysis of these bacterial genomes to detect the genomic features that might be associated with the locations of ori and ter, including AT and GC skews [16, 20]. and purine and keto excesses [24]. Methods based on wavelet transforms generally require powerful visualization tools. In the implementation, we analyzed the genomes for these indices using C++ codes, performed wavelet transformations via Matlab, and made graphics with the Xmgrace Graphic software on MACI-cluster parallel computers.
AT and GC skews
Cumulative AT skew (ATS) was defined as the sum of (A-T)/(A+T) in adjacent windows and was determined by

and, similarly, cumulative GC skew (GCS) was defined as the sum of (G-C)/(G+C) in adjacent windows and was determined by

where n is the window size and N is the chromosome length.
Purine and keto excesses
Purine excess was defined as the sum of all purines (AG) minus the sum of all pyrimidines (TC) encountered in a walk along the sequence up to the point plotted and was determined by

and, similarly, keto excess was defined as the sum of all keto bases (GT) minus that of the amino bases (AC) and was determined by

where N is chromosome length, and B is the number of the particular base (A, C, G or T) occurring at the i th location.
Wavelet transform methods
Wavelet analysis has become a common tool for documenting localized variations of power within a time series, with successful applications in signal and image processing, numerical analysis and statistics. The basic procedure is to adopt a prototype function, called an analyzing wavelet or mother wavelet, and represent the signal using scaled and shifted versions of this function. Because the original function can be represented in terms of a wavelet expansion, data manipulations can be performed using corresponding wavelet coefficients. The wavelet transform is especially useful in detecting singularities in the presence of noise by examining the maxima in the modulus of the wavelet transform. In particular, we sought the abscissa where the maxima converge at fine scales. These maxima indicate positions of high curvature in a smoothed version of the signal and thus will indicate the presence of corners. At coarse scales, noise is unimportant and maxima are easy to identify, although their locations are not precise (the smoothing has "blurred" the signal). At fine scales, the smoothing is less strong, and the locations are more precise. On the other hand, at finer scales the signal-to-noise ratio becomes more dominant, so the maxima are harder to identify. As a result, the technique of following the lines of maxima from coarse to fine scales allows us to retain the advantages of both coarse- and fine-scale analysis.
We employed the continuous real wavelet transform [27] and our analyzing wavelet is the normalized first derivative of a Gaussian function:

where σ is a scaling factor. The real wavelet transform of a function f is

In order to apply this transform to a vector x of length N, x is taken to correspond to samples at the points t 0 = 0, t 1 = 1/ N, t = 2/N,...,t N = 1 - 1/N of a 1-periodic function x(t). The wavelet transform Wx, for a range of scales s, is then calculated in the Fourier domain using the Fast Fourier Transform. The result is a two-dimensional array of values of Wx at positions t and scale s.
Models
Two distinct models were employed: one for the AT and GC skews and one for the purine- and keto-excesses. For AT or GC skew, the signals were modelled with two binomial distributions in each strand. To take the AT skew as an example, the first provides the probability of obtaining a count of k A's and T's in a window of length n as

and the second gives the probability of j of those being A's (and so k-j being T's) as

For purine or keto excess, the raw signals were analyzed, given by the moving differences of the cumulative sum. This would result in a sequence of 1's and -1's, modelled as being drawn from a simple binomial distribution in each strand, with a probability p i of drawing a 1 and 1-p i of drawing a - 1.
Significance levels and the null hypothesis
In order to determine the significance levels for our data, i.e., the identification of the joins between the two replicores (halves of the chromosome between ori and ter), we used the null hypothesis that the signal was generated according to the above models, but with p i = 0.5 and q i = 0.5 in each replicore, so that the signals should be homogenous. Artificial signals were created using this hypothesis, with their wavelet transforms calculated. At each scale, this resulted in a sequence of wavelet coefficients, and the distribution of the values in this sequence was used to determine significance levels for the wavelet coefficients computed from the original signal.
Confidence intervals
In order to understand and calibrate the performance of the wavelet estimator, Monte-Carlo simulation was employed. For the keto and purine excess signals, rough estimates of the probabilities p i and the locations of the joins between the two replicores were obtained by examining the cumulative sums and locating the maximum and minimum values. For the AT and GC skews, the value of q i was assumed to be 0.5, and the probabilities p i were estimated as for the previous signals. Then 1000 simulated signals were created with the same properties, according to the models described above, and the wavelet estimator was used to recover the locations of the joins between the two replicores. The distribution of the resulting estimates is then used to deduce confidence intervals for the results from the wavelet estimator applied to the original signal. However, many of the signals were too long to make the creation and estimation of 1000 simulated signals and 1000 runs a realistic task. In this case, the simulations were repeated using shorter signals, with a succession of different lengths, and the results were extrapolated to the length of the original signal.
Using this method, we analyzed 40 bacterial chromosomes and located the putative positions for ori and ter by AT skew, GC skew, keto excess and purine excess. We then tested their statistical significance at 5% level. To increase the accuracy and comparative power, we adopted a 100 bp small moving window size in the GC and AT skew analysis. Finally, we used wavelet transformation to analyze all indices, to find significance regions and confidence intervals at 95% level and to test the significant peak at 5% level.
References
Bird RE, Louarn J, Martuscelli J, Caro L: Origin and sequence of chromosome replication in Escherichia coli. J Mol Biol. 1972, 70: 549-566.
Hill TM, Henson JM, Kuempel PL: The terminus region of the Escherichia coli chromosome contains two separate loci that exhibit polar inhibition of replication. Proc Natl Acad Sci USA. 1987, 84: 1754-1758.
Hill TM, Pelletier AJ, Tecklenburg ML, Kuempel PL: Identification of the DNA sequence from the E. coli terminus region that halts replication forks. Cell. 1988, 55: 459-466.
Hidaka M, Akiyama M, Horiuchi T: A consensus sequence of three DNA replication terminus sites on the E. coli chromosome is highly homologous to the terR sites of the R6K plasmid. Cell. 1988, 55: 467-75.
Marians KJ: Prokaryotic DNA replication. Annu Rev Biochem. 1992, 61: 673-719. 10.1146/annurev.biochem.61.1.673.
Marczynski GT, Shapiro L: Bacterial chromosome origins of replication. Curr Opin Genet Dev. 1993, 3: 775-82.
Baker TA: Replication arrest. Cell. 1995, 80: 521-524.
Liu SL, Sanderson KE: Rearrangements in the genome of the bacterium Salmonella typhi. 1995. Proc Natl Acad Sci USA. 1995, 92: 1018-1022.
Liu SL, Sanderson KE: The genomic cleavage map of Salmonella typhi Ty2. J Bacteriol. 1995, 177: 5099-5107.
Liu SL, Sanderson KE: Highly plastic chromosomal organization in Salmonella typhi. Proc Natl Acad Sci USA. 1996, 93: 10303-10308. 10.1073/pnas.93.19.10303.
Blattner FR, Plunkett G, Bloch CA, Perna NT, Burland V, Riley M, Collado-Vides J, Glasner JD, Rode CK, Mayhew GF, Gregor J, Davis NW, Kirkpatrick HA, Goeden MA, Rose DJ, Mau B, Shao Y: The complete genome sequence of Escherichia coli K-12. Science. 1997, 277: 1453-1462. 10.1126/science.277.5331.1453.
Liu SL, Schryvers AB, Sanderson KE, Johnston RN: Bacterial phylogenetic clusters revealed by genome structure. J Bacteriol. 1999, 181: 6747-6755.
Liu GR, Rahn A, Liu WQ, Sanderson KE, Johnston RN, Liu SL: The evolving genome of Salmonella pullorum. J Bacteriol. 2002, 184: 2626-2633. 10.1128/JB.184.10.2626-2633.2002.
Kunst F, Ogasawara N, Moszer I, Albertini AM: The complete genome sequence of the Gram-positive bacterium Bacillus subtilis. Nature. 1997, 390: 249-256. 10.1038/36786.
Furusawa M, Doi H: Promotion of evolution: disparity in the frequency of strand-specific misreading between the lagging and leading DNA strands enhances disproportionate accumulation of mutations. J Theor Biol. 1992, 157: 127-133.
Lobry JR: Asymmetric substitution patterns in the two DNA strands of bacteria. Mol Biol Evol. 1996, 13: 660-665.
Lobry JR: A simple vectorial representation of DNA sequences for the detection of replication origins in bacteria. Biochimie. 1996, 78: 323-326. 10.1016/0300-9084(96)84764-X.
Lobry JR: Origin of replication of Mycoplasma genitalium. Science. 1996, 272: 745-746.
McLean MJ, Wolfe KH, Devine KM: Base composition skews, replication orientation, and gene orientation in 12 prokaryote genomes. J Mol Evol. 1998, 47: 691-696.
Grigoriev A: Analyzing genomes with cumulative skew diagrams. Nucleic Acids Res. 1998, 26: 2286-2290. 10.1093/nar/26.10.2286.
Picardeau M, Lobry JR, Hinnebusch BJ: Physical mapping of an origin of bidirectional replication at the centre of the Borrelia burgdorferi linear chromosome. Mol Microbiol. 1999, 32: 437-445. 10.1046/j.1365-2958.1999.01368.x.
Grigoriev A: Strand-specific compositional asymmetries in double-stranded DNA viruses. Virus Res. 1999, 60: 1-19. 10.1016/S0168-1702(98)00139-7.
Salzberg SL, Salzberg AJ, Kerlavage AR, Tomb JF: Skewed oligomers and origins of replication. Gene. 1998, 217: 57-67. 10.1016/S0378-1119(98)00374-6.
Freeman JM, Plasterer TN, Smith TF, Mohr SC: Patterns of genome organization in bacteria. Science. 1998, 279: 1827-10.1126/science.279.5358.1827a.
Torrence C, Compo GP: A Practical Guide to Wavelet Analysis. Bull Amer Meteor Soc. 1988, 79: 61-78. 10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2.
Arneodo A, Bacry E, Graves PV, Muzy JF: Characterizing long-range correlations in DNA sequences from wavelet analysis. Physical Rev Lett. 1995, 74: 3293-3296. 10.1103/PhysRevLett.74.3293.
Arneodo A, Audit B, Bacry E, Manneville S, Muzy JF, Roux SG: Thermodynamics of fractal signals based on wavelet analysis: application to fully developed turbulence data and DNA sequences. Physica A. 1998, 254: 24-45. 10.1016/S0378-4371(98)00002-8.
Lio P, Vannucci M: Finding pathogenesis islands and gene transfer events in genome data. Bioinformatics. 2000, 16: 932-940. 10.1093/bioinformatics/16.10.932.
Dodin G, Vandergheynst P, Levoir P, Cordier C, Marcourt L: Fourier and wavelet transform analysis, a tool for visualizing regular patterns in DNA sequences. J Theor Biol. 2000, 206: 323-326. 10.1006/jtbi.2000.2127.
Audit B, Vaillant C, Arneodo A, d'Aubenton-Carafa Y, Thermes C: Long-range correlations between DNA bending sites: relation to the structure and dynamics of nucleosomes. J Mol Biol. 2002, 316: 903-18. 10.1006/jmbi.2001.5363.
Frank AC, Lobry JR: Asymmetric substitution patterns: a review of possible underlying mutational or selective mechanisms. Gene. 1999, 238: 65-77. 10.1016/S0378-1119(99)00297-8.
Grigoriev A, Freeman JM, Plasterer TN, Smith TF, Mohr SC: Gnomic arithmetic. Science. 1998, 281: 1923a-10.1126/science.281.5385.1923a.
Perna NT, Plunkett GI, Burland V, Mau B, Glasner JD, Rose DJ, Mayhew GF, Evans PS, Gregor J, Kirkpatrick HA, Posfai G, Hackett J, Klink S, Boutin A, Shao Y, Miller L, Grotbeck EJ, Davis NW, Lim A, Dimalanta ET, Potamousis KD, Apodaca J, Anantharaman TS, Lin J, Yen G, Schwartz DC, Welch RA, Blattner FR: Genome sequence of enterohaemorrhagic Escherichia coli O157:H7. Nature. 2001, 409: 529-533. 10.1038/35054089.
Lawrence JG, Ochman H: Amelioration of bacterial genomes: rates of change and exchange. J Mol Evol. 1997, 44: 383-397.
Acknowledgements
We thank R. N. Johnston for his encouragement and support for this work and C. Sensen, D. Phillips and T. Fung for their assistance with computing facilities.
This study was supported by a grant from the "985" Foundation of Peking University, a grant from the government of China for overseas Chinese Scholars, and operating grants from the Medical Research Council of Canada (MRC, Grant # GOP-38106), the Natural Sciences and Engineering Research Council of Canada (NSERC, Grant # 216912-00), and the Canadian Institutes for Health Research (CIHR, Grant # MOP-47817).
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
JZS and AW carried out all computational work and drafted the first manuscript, and SLL coordinated the work and drafted the final manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Song, J., Ware, A. & Liu, SL. Wavelet to predict bacterial ori and ter: a tendency towards a physical balance. BMC Genomics 4, 17 (2003). https://doi.org/10.1186/1471-2164-4-17
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2164-4-17