Abstract
The breakpoint graph and the de Bruijn graph are two key data structures in the studies of genome rearrangements and genome assembly. However, the classical breakpoint graphs are defined on two genomes (represented as sequences of synteny blocks), while the classical de Bruijn graphs are defined on a single genome (represented as DNA strings). Thus, the connection between these two graph models is not explicit. We generalize the notions of both the breakpoint graph and the de Bruijn graph, and make it transparent that the breakpoint graph and the de Bruijn graph are mathematically equivalent. The explicit description of the connection between these important data structures provides a bridge between two previously separated bioinformatics communities studying genome rearrangements and genome assembly.
Similar content being viewed by others
Introduction
The de Bruijn graph is a data structure first brought to bioinformatics as a method to assemble genomes from the experimental data generated by sequencing by hybridization [1]. It later became the key algorithmic technique in genome assembly [2, 3] that resulted in dozens of software tools [4–12]. In addition, the de Bruijn graphs have been used for repeat classification [13], de novo protein sequencing [14], synteny block construction [15, 16], multiple sequence alignment [17], and other applications in genomics and proteomics.
The breakpoint graph is a data structure introduced to study the reversal distance [18], which has formed the basis for much algorithmic research on rearrangements over the last two decades [19].
Since the connections between the breakpoint graphs and the de Bruijn graphs was never explicitly described, researchers studying genome rearrangements often do not realize that breakpoint graphs are merely de Bruijn graphs in disguise. As a result, they often do not know how to move from the traditional breakpoint graphs on synteny blocks to the breakpoint graphs on genomes (with "single nucleotide" resolution), particularly in the case of double-stranded genomes with inverted repeats. Likewise, researchers working in genome assembly are often unaware about the connections between the de Bruijn graphs and the breakpoint graphs. As a result, the exchange of ideas between these two communities has been limited. For example, Iqbal et al. [20] recently introduced the notion of the colored de Bruijn graphs that resulted in a popular Cortex assembler. While the notion of the colored de Bruijn graphs is essentially identical to the notion of the breakpoint graph, authors of [20] are probably unaware about this connection since they provided no references to previous genome rearrangement studies. This is unfortunate since various results about the breakpoint graphs (e.g., the connection between rearrangements and alternating cycles) remained beyond the scope of this very useful study.
Recently, genome rearrangement studies moved from the level of synteny blocks to the level of single nucleotides [21]. Likewise, genome assembly experts recently moved towards the analysis of structural variations and comparative assembly of related species based on the analysis of the de Bruijn graphs [20]. We thus argue that the time has come to explain that the breakpoint graphs and the de Bruijn graphs are two identical data structures (if one ignores a cosmetic difference between them) as they both represent specific instances of a general notion of the A-Bruijn graph introduced in [13]. The A-Bruijn graphs are based on representing genomes as sets of labeled paths and further gluing identically labeled edges (breakpoint graphs) or vertices (de Bruijn graphs) in the resulting paths.
We argue that a unified framework covering both breakpoint and de Bruijn graphs is important to bridge the divide between researchers working with breakpoint graphs (that usually focus in rearrangements and ignore repeats) and researchers working with de Bruijn graphs (that usually focus on repeats and ignore rearrangements). In reality, there exists a complex interplay between rearrangements and repeats, e.g., LINE repeats and segmental duplications often trigger rearrangements [22–24]. However, this interplay is not explicitly revealed by the breakpoint graphs since they do not even encode repeats (repeats are intentionally masked at the synteny block construction step). For example, the interplay between LINEs and rearrangements cannot be derived from the breakpoint graph alone forcing Zhao and Bourque [23] to perform additional analysis. Our goal is to introduce the graphs that encode both rearrangements and repeats and immediately reveal this interplay. For example, encoding repeats present in the breakpoint regions (that may potentially trigger rearrangements) leads to gluing alternating cycles in the breakpoint graphs and requires development of new algorithms that integrate rearrangements and repeats. In such graphs, the classical non-self-intersecting alternating cycles formed by edges alternating between two colors (the workhorse of genome rearrangement studies) may turn into self-intersecting cycles formed by edges alternating between 3 colors, where the third color corresponds to repeated elements (see Figure 1). Nurk and Pevzner [25] recently used this framework to develop a new comparative genome analysis tool SPArcle and applied it to analyzing multiple bacterial strains resulting from the "controlled evolution" experiments [26]. SPArcle is based on SPAdes assembler and, in difference from Cortex, it uses ideas from the previous genome rearrangement studies (e.g., alternating cycles) to analyze the resulting A-Bruijn graphs.
Genomes G A = S 1 , S 2 , S 3 and G B = S 1 , − S 2 , S 3 (represented as bicolored paths) differ from each other by a single reversal of segment S 2 . The breakpoint graph BP(G A , G B ) and the alternating cycle constructed from genomes G A and G B (left: no repeats at the breakpoint regions; right, a pair of repeats colored in green at the breakpoint regions).
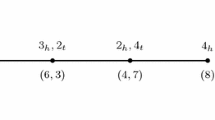
Genome rearrangement studies usually start from constructing a set of synteny blocks shared by two genomes (see Figure 2). Each genome is defined as a sequence of synteny blocks separated by breakpoint regions and is represented as a path formed by alternating colored and black edges, where synteny blocks correspond to directed and labeled black edges and breakpoint regions correspond to undirected colored edges. Figure 3(a) presents paths corresponding to 11 synteny blocks shared by Human and Mouse × chromosomes. Each synteny block S i is represented as an directed black edge , where and refer to the endpoints of the synteny blocks representing its tail and head, respectively. Two consecutive synteny blocks are separated by a breakpoint region in the Human (Mouse) × chromosome that is modeled by a red (blue) edge connecting the corresponding endpoints of these synteny blocks. The (traditional) breakpoint graph of Human and Mouse × chromosomes is obtained by "gluing" identically labeled black edges in these two paths as shown in Figure 3.
The 11 synteny blocks shared by Human and Mouse × chromosomes (adapted from Pevzner and Tesler [33]).
The multiple breakpoint graphs [27] are constructed from a set of k > 2 genomes using the same procedure. While every synteny block appears just once in each of the genomes shown above, the definition of the breakpoint graph naturally extends to the case when a synteny block appears multiple times (or does not appear in a particular genome).
The classical de Bruijn graph is defined on a single genome (represented as a DNA string), while the classical breakpoint graph is defined on two genomes (represented as sequences of synteny blocks). Since synteny blocks are DNA strings, the question arises whether one can study both the de Bruijn graph and the breakpoint graph in the same framework, and what is the difference between the de Bruijn graph and the breakpoint graph.
In this paper, we generalize the definitions of both the de Bruijn graph and the breakpoint graph for both single and multiple genomes and for both single-stranded and double-stranded cases. We further show that the breakpoint graph and the de Bruijn graph are mathematically equivalent.
A single genome (single-stranded case)
We now generalize the definition of the breakpoint graph to a single DNA strings. Traditionally, breakpoint graphs were defined on the set of synteny blocks rather than directly on DNA strings. Given a string String, we define its "synteny blocks" as its (k-1)-mers, represent each (k-1)-mer by a directed black edge, and construct an alternating path, denoted Path BP (String, k), by inserting directed colored edges between consecutive (k-1)-mers. The breakpoint graph is obtained by gluing identical (k-1)-mers (directed black edges) in this path. It is easy to see that each breakpoint region connects 2 consecutive (k-1)-mers and thus corresponds to a kmer. The breakpoint graph of a string String, denoted BP (String, k), is shown in Figure 4.
Given a string String = s1s2 . . . s n , the de Bruijn graph DB(String, k) is defined as follows. The string String is represented as a colored path Path DB (String, k), whose (n − k + 1) edges are labeled by k-mers, s1s2 . . . s k , s2s3 . . . s k+1 , . . ., and sn−k+1sn−k+2 . . . s n . Implicitly, each vertex in the path is labeled by a (k-1)-mer. The de Bruijn graph DB(String, k) results from gluing identically labeled vertices in the path [28]. Figure 5 shows the de Bruijn graph on the same string as in Figure 4.
Comparison of Figure 4 and 5 reveals that BP (String, k) is equivalent to DB(String, k). BP (String, k) can be converted into DB(String, k) by collapsing all black edges, while DB(String, k) can be converted into BP (String, k) by expanding each vertex v into a directed edge (v′, v″) in such a way that all incoming edges into v (outgoing edges from v) become incoming edges into v′ (outgoing edges from v″). Table 1 summarizes the correspondence between BG(String, k) and DB(String, k).
We note that while the notions of the breakpoint graph and the de Bruijn graph were defined for a single string, the same definition works for a set of strings (see Figure 6).
Multiple genomes (single-stranded case)
Given genomes G A and G B (represented as sets of strings), we classify their k-mers into 3 classes: A (occur only in G A ), B (occur only in G B ) and AB (occur in both G A and G B ).
The breakpoint graph BP (G A , G B , k) is simply coloring the k-mer edges of the breakpoint graph BP(G A ∪ G B , k) into 3 colors: A (blue), B (red) and AB (green) (Figure 7). Similarly, the de Bruijn graph DB(G A , G B , k) is simply coloring the edges of the de Bruijn graph DB(G A ∪ G B , k) into 3 colors: A (blue), B (red) and AB (green) (see Figure 8).
In practice, both BP (G A , G B , k) and DB(G A , G B , k) are often condensed as follows.
A non-branching directed path consisting of 3 edges is called condensible in BP(G A , G B , k) if its middle edge is black and its starting and ending edges have the same color C. We substitute a condensible path by a single directed edge colored C with the same direction as the direction of the path. The condensed breakpoint graph CBP(G A , G B , k) iteratively replaces all condensible paths by single edges in BP(G A , G B , k) (Figure 7(c)). A new edge resulting from condensing a nonbranching path formed by edges e1, e2, and e3 is assigned a label whose prefix is a label of e1 and whose suffix is the label of e3 (labeling of edges in the condensed graphs is not the focus of this paper and is not discussed in the examples below).
A non-branching directed path consisting of 2 edges is called condensible in DB(G A , G B , k) if its starting and ending edges have the same color C. We substitute a condensible path by a single edge colored C with the same direction as the direction of the path. The condensed de Bruijn graph CDB(G A , G B , k) iteratively replaces all condensible paths by single edges in DB(G A , G B , k) (Figure 8(c)).
Note that both the condensed breakpoint graph in Figure 7(c) and the condensed de Bruijn graph in Figure 8(c) reveal an alternating red-blue cycle on 6 edges, a signature of a transposition. While researchers working on genome rearrangements are well aware about alternating cycles in the breakpoint graphs, the researchers working on de Bruijn graphs may not know that these cycles represent fingerprints of rearrangements.
Figure 7 and 8 illustrate that BP(G A , G B , k) is mathematically equivalent to DB(G A , G B , k). BP (G A , G B , k) can be converted into DB(G A , G B , k) by collapsing all black edges, while DB(G A , G B , k) can be converted into BP(G A , G B , k) by expanding all vertices. It is the same for the condensed case. Table 2 summarizes the comparison between DB(G A , G B , k) and BP(G A , G B , k).
While the above notions of the breakpoint graph and the de Bruijn graph were defined for 2 genomes, they naturally generalize to any number of genomes [27].
A single genome (double-stranded case)
We now generalize the notions of the de Bruijn and breakpoint graphs from single-stranded to double-stranded genomes. Instead of the explicit representation of both strands (like in most existing assemblers), we describe a more efficient representation that encodes both strands in a single canonical strand (compare with similar representations of both strands in SPAdes [12] and some other assemblers).
For a nucleotide x, we denote its complementary nucleotide as , e.g., T and . Given a k-mer s = s1s2 . . . sk, we define its reverse complement as the k-mer . We call a k-mer canonical if it is smaller or equal (in the lexicographic order) than its reverse complement. For example, AG and AT are canonical 2-mers but CT is not a canonical 2-mer. In this section, we will represent strings as paths labeled only by canonical k-mers and will define the breakpoint and de Bruijn graphs as the results of gluing these paths.
While DB(String, k) and BP (String, k) glue identical (k-1)-mers in String, these graphs were not designed to glue a (k-1)-mer with its reverse complement (see Figure 9). In many applications, gluing (k-1)-mers with their reverse complements would be beneficial; for example, developers of many genome assemblers invest significant efforts in maintaining the "symmetric" de Bruijn graphs at all stages of the assembly so that the subgraph representing one strand is topologically identical to the subgraph representing another strand [12]. Since the breakpoint graph and the de Bruijn graph in Figure 9 do not allow one to analyze the interplay between rearrangements and inverted repeats, we need to come up with a new graph-theoretical model for double-stranded genomes. We note that since A-Bruijn graphs were designed to accommodate gluing of arbitrary positions in String (as long as they are defined as "aligned" in the A-Bruijn graph framework [13]), gluing (k-1)-mers with their reverse complements perfectly fits in the framework of the A-Bruijn graphs.
To model double-stranded strings as paths, we introduce the concept of a canonical path representing a string String (that differs from the standard representation of String as a path from Section 2). To transform a standard path Path BP (String, k) into a canonical path CPathBP (String, k), we reverse directions of all black edges labeled by non-canonical (k-1)-mers and change their labels into their reverse complements (see Figure 10, left). As a result, all black edges in the canonical path are labeled by canonical (k-1)-mers.
A string String = ACAGTCA (top) represented by canonical paths CPath BP ( String , 3) and CPath DB ( String , 3), the double-stranded breakpoint graph BP *( String , 3) (left) and the double-stranded de Bruijn graph DB *( String , 3) (right). A pair of repeats in String is shown in brown and a pair of inverted repeats is shown in red.
To transform a standard path Path DB (String, k) into a canonical path CPath DB (String, k), we simply change labels of all vertices labeled by non-canonical (k-1)-mers into their reverse complements (see Figure 10, right).
After transforming standard paths Path BP (String, k) and Path DB (String, k) into a canonical paths CPath BP (String, k) and CPath DB (String, k) respectively, the definition of the breakpoint graph (gluing of identically labeled black edges in CPath BP (String, k)) and the de Bruijn graph (gluing of identically labeled vertices in CPath BP (String, k)) remain unchanged. Pairs of k-mer edges are also glued if they represent the reverse complement k-mer of each other and are labeled by both k-mers. The graphs obtained after gluing these paths are called the double-stranded breakpoint graph BP* (String, k) and the double-stranded de Bruijn graph DB* (String, k) (Figure 10). While BP*(String, k) makes use of the direction of the black edge to represent whether the canonical string or its reverse complement is
used, DB* (String, k) collapses all black edges into vertices and no longer maintains the direction information to distinguish these two possibilities. A pair of vertices in DB* (String, k) labeled by canonical (k-1)-mers v and w may potentially correspond to 4 types of edges depending on whether the edge connects (i) v and w, (ii) v and , (iii) and w, and (iv) and (compare to the bi-directed de Bruijn graph [29]).
As before, DB*(String, k) is obtained from BP*(String, k) by collapsing all black edges, while BP*(String, k) is obtained from DB*(String, k) by expanding all vertices into black edges (and connecting black edges according to the labels on the colored edges).
One may notice that while the double-stranded de Bruijn graph is similar to the bi-directional de Bruijn graph introduced in [29], it does not require the explicit introduction of the bi-directional edges. The notions of the double-stranded breakpoint graphs and de Bruijn graphs also can be naturally extended from a single double-stranded string to multiple double-stranded strings.
Multiple genomes (double-stranded case)
Given a string String = s1s2 . . . si−1s i s i+1 . . . s j−1 s j s j+1 . . . s n−1 s n , a reversal of the segment s i s i+1 . . . s j−1 sj results in a string where this segment is substituted by its reverse complement. Below we illustrate that reversals are represented as usual alternating blue-red cycles in the condensed double-stranded breakpoint and de Bruijn graphs.
Given two genomes G A and G B , we classify each k-mer s into 3 classes: A (if either s or belongs to G A but neither s or belongs to G B ), B (if either s or belongs to G B but neither s or belongs to G A ) and AB (if both G A and G B contain either S or ).
The double-stranded breakpoint graph BP*(G A , G B , k) is simply coloring the edges in BP* (G A ∪ G B , k) into 3 colors: A (blue), B (red) and AB (green) (Figure 11). Similarly, the double-stranded de Bruijn graph DB*(G A , G B , k) is simply coloring the edges in DB*(G A ∪ G B , k) into 3 colors: A (blue), B (red) and AB (green) (Figure 12).
The double-stranded breakpoint graph BP *( GA, GB , 4) and the condensed double-stranded breakpoint graph CBP *( GA, GB , 4) of two genomes G A and G B . Each of 3 synteny blocks in both BP*(G A , G B , 4) and CBP* (G A , G B , 4) is represented as a path (starting and ending in black edges and having a green edge in the middle).
Both BP*(G A , G B , k) and DB*(G A , G B , k) can be further condensed as described in Table 2 resulting in the condensed double-stranded breakpoint graph CBP* (G A , G B , k) and the condensed double-stranded de Bruijn graph CDB*(G A , G B , k), respectively (Figure 11(c) and Figure 12(c)).
As before, BP*(G A , G B , k) (CBP*(G A , G B , k)) is obtained from DB*(G A , G B , k) (CDB*(G A , G B , k)) by collapsing all black edges, while DB*(G A , G B , k) (CDB* (G A , G B , k)) is obtained from BP*(G A , G B , k) (CBP*(G A , G B , k)) by expanding all vertices into black edges (and connecting black edges according to the labels on the colored edges).
While the above notions of the double-stranded breakpoint graph and the double-stranded de Bruijn graph were defined for 2 genomes, they naturally generalize to any number of genomes.
Conclusion
We described the connection between the breakpoint graph and the de Bruijn graph that reveals that these constructions (that have been treated as two different data structures for over two decades) are essentially identical. We believe that the explicit description of this connection will contribute to a dialog between two previously separated bioinformatics communities studying genome rearrangements and genome assembly. It may also clarify the connection between the breakpoint graph, the de Bruijn graph, and the string graph introduced by Myers [30], another powerful paradigm for genome assembly. As hinted by Pop [31], the string graphs are functionally equivalent to the de Bruijn graphs, e.g., the comparison of Figure 1 in [30] and Figure 2 in [13]) suggests that the string graph is a special case of the ABruijn graph. Simpson and Durbin [32] further suggested that the de Bruijn graph and the string graph constructions on all the k-mers of a genome (using parameter τ = k − 1 for the string graph) are equivalent. However, the explicit description of this equivalence is still missing and we hope that the proposed A-Bruijn graph framework can be further extended to cover the string graphs as well.
References
Pevzner PA: l-tuple DNA sequencing: computer analysis. J Biomol Struct Dyn. 1989, 7: 63-73.
Idury RM, Waterman MS: A new algorithm for DNA sequence assembly. J Comput Biol. 1995, 2 (2): 291-306. 10.1089/cmb.1995.2.291.
Pevzner PA, Tang H, Waterman MS: An Eulerian path approach to DNA fragment assembly. Proc Nat'l Acad Sci USA. 2001, 98 (17): 9748-10.1073/pnas.171285098.
Zerbino DR, Birney E: Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Research. 2008, 18 (5): 821-829. 10.1101/gr.074492.107.
Chaisson MJ, Pevzner PA: Short read fragment assembly of bacterial genomes. Genome Research. 2008, 18 (2): 324-330. 10.1101/gr.7088808.
Simpson JT, Wong K, Jackman SD, Schein JE, Jones SJM, Birol I: Abyss: a parallel assembler for short read sequence data. Genome Research. 2009, 19 (6): 1117-1123. 10.1101/gr.089532.108.
Peng Y, Leung H, Yiu S, Chin F: IDBA - a practical iterative de Bruijn graph de novo assembler. Proc 14th Int'l Conf Comput Mol Biol (RECOMB'10) Lecture Notes in Comp Sci. 2010, 6044: 426-440.
Butler J, MacCallum I, Kleber M, et al: ALLPATHS: de novo assembly of whole-genome shotgun microreads. Genome Research. 2008, 18 (5): 810-820. 10.1101/gr.7337908.
Boisvert S, Laviolette F, Corbeil J: Ray: simultaneous assembly of reads from a mix of high-throughput sequencing technologies. J Comput Biol. 2010, 17 (11): 1519-1533. 10.1089/cmb.2009.0238.
Li R, Zhu H, Ruan J, et al: De novo assembly of human genomes with massively parallel short read sequencing. Genome Research. 2010, 20 (2): 265-272. 10.1101/gr.097261.109.
Chitsaz H, Yee-Greenbaum JL, Tesler G, et al: Efficient de novo assembly of single-cell bacterial genomes from short-read data sets. Nature biotechnology. 2011
Bankevich A, Nurk S, et al: SPAdes: A new genome assembly algorithm and its applications to single-cell sequencing. J Comput Biol. 2012, 19 (5): 455-477. 10.1089/cmb.2012.0021.
Pevzner PA, Tang H, Tesler G: De novo repeat classification and fragment assembly. Genome Research. 2004, 14 (9): 1786-1796. 10.1101/gr.2395204.
Böcker S: Sequencing from compomers: Using mass spectrometry for dna de novo sequencing of 200+ nt. J Comput Biol. 2004, 11 (6): 1110-1134. 10.1089/cmb.2004.11.1110.
Pham SK, Pevzner PA: DRIMM-Synteny: decomposing genomes into evolutionary conserved segments. Bioinformatics. 2010, 26 (20): 2509-2516. 10.1093/bioinformatics/btq465.
Minkin I, Patel A, Kolmogorov M, Vyahhi N, Pham S: Sibelia: a scalable and comprehensive synteny block generation tool for closely related microbial genomes. Proc 13th Workshop Algs in Bioinf (WABI'13) Lecture Notes in Comp Sci. 2013, 8126: 215-229. 10.1007/978-3-642-40453-5_17.
Raphael B, Zhi D, Tang H, Pevzner PA: A novel method for multiple alignment of sequences with repeated and shuffled elements. Genome Research. 2004, 14 (11): 2336-2346. 10.1101/gr.2657504.
Bafna V, Pevzner PA: Genome rearrangements and sorting by reversals. Proc 34th Ann IEEE Symp Foundations of Comput Sci (FOCS'93). 1993, 148-157.
Fertin G, Labarre A, Rusu I, Tannier E, Vialette S: Combinatorics of Genome Rearrangements. MIT Press, Inc
Iqbal Z, Caccamo M, Turner I, Flicek P, McVean G: De novo assembly and genotyping of variants using colored de bruijn graphs. Nature genetics. 2012, 44 (2): 226-232. 10.1038/ng.1028.
Boussau B, Daubin V: Genomes as documents of evolutionary history. Trends in ecology & evolution. 2010, 25 (4): 224-232. 10.1016/j.tree.2009.09.007.
Bailey JA, Baertsch R, Kent WJ, Haussler D, Eichler EE: Hotspots of mammalian chromosomal evolution. Genome Biology. 2004, 5 (4): 23-10.1186/gb-2004-5-4-r23.
Zhao H, Bourque G: Recovering genome rearrangements in the mammalian phylogeny. Genome Research. 2009, 19 (5): 934-942. 10.1101/gr.086009.108.
Alekseyev MA, Pevzner PA: Comparative genomics reveals birth and death of fragile regions in mammalian evolution. Genome Biology. 2010, 11 (11): 117-10.1186/gb-2010-11-11-r117.
Nurk S, Pevzner PA: Sparcle: using colored de bruijn graphs for analysing genome variations, unpublished manuscript.
Guzman GI, Utrilla J, Monk JM, Brunk E, Ebrahim A, Nurk S, Palsson BO, Feist AM: Model-driven discovery of 'underground' isozyme functions in escherichia coli, unpublished manuscript.
Alekseyev MA, Pevzner PA: Breakpoint graphs and ancestral genome reconstructions. Genome Research. 2009, 19 (5): 943-957. 10.1101/gr.082784.108.
Compeau PEC, Pevzner PA: Bioinformatics Algorithms: An Active-Learning Approach.
Medvedev P, Georgiou K, Myers G, Brudno M: Computability of models for sequence assembly. Proc 7th Workshop Algs in Bioinf (WABI'07) Lecture Notes in Comp Sci. 2007, 4645: 289-301. 10.1007/978-3-540-74126-8_27.
Myers EW: The fragment assembly string graph. Bioinformatics. 2005, 21 (suppl 2): 79-85.
Pop M: Genome assembly reborn: recent computational challenges. Briefings in bioinformatics. 2009, 10 (4): 354-366. 10.1093/bib/bbp026.
Simpson JT, Durbin R: Efficient construction of an assembly string graph using the fm-index. Bioinformatics. 2010, 26 (12): 367-373. 10.1093/bioinformatics/btq217.
Pevzner PA, Tesler G: Genome rearrangements in mammalian evolution: lessons from human and mouse genomes. Genome Research. 2003, 13 (1): 37-45. 10.1101/gr.757503.
Acknowledgements
YL was supported by the Swiss National Science Foundation (grant no. 146708). SN and PAP were supported by the Government of the Russian Federation (grant no. 11.G34.31.0018).
Declarations
Publication costs for this article were funded by St. Petersburg Academic University.
This article has been published as part of BMC Genomics Volume 15 Supplement 6, 2014: Proceedings of the Twelfth Annual Research in Computational Molecular Biology (RECOMB) Satellite Workshop on Comparative Genomics. The full contents of the supplement are available online at http://www.biomedcentral.com/bmcgenomics/supplements/15/S6.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
PAP conceived the study. YL, SN and PAP performed the analysis. YL and PAP wrote the paper with help from SN. All authors read and approved the final manuscript.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Lin, Y., Nurk, S. & Pevzner, P.A. What is the difference between the breakpoint graph and the de Bruijn graph?. BMC Genomics 15 (Suppl 6), S6 (2014). https://doi.org/10.1186/1471-2164-15-S6-S6
Published:
DOI: https://doi.org/10.1186/1471-2164-15-S6-S6