Abstract
Background
The pattern and timing of the rise in complex multicellular life during Earth's history has not been established. Great disparity persists between the pattern suggested by the fossil record and that estimated by molecular clocks, especially for plants, animals, fungi, and the deepest branches of the eukaryote tree. Here, we used all available protein sequence data and molecular clock methods to place constraints on the increase in complexity through time.
Results
Our phylogenetic analyses revealed that (i) animals are more closely related to fungi than to plants, (ii) red algae are closer to plants than to animals or fungi, (iii) choanoflagellates are closer to animals than to fungi or plants, (iv) diplomonads, euglenozoans, and alveolates each are basal to plants+animals+fungi, and (v) diplomonads are basal to other eukaryotes (including alveolates and euglenozoans). Divergence times were estimated from global and local clock methods using 20–188 proteins per node, with data treated separately (multigene) and concatenated (supergene). Different time estimation methods yielded similar results (within 5%): vertebrate-arthropod (964 million years ago, Ma), Cnidaria-Bilateria (1,298 Ma), Porifera-Eumetozoa (1,351 Ma), Pyrenomycetes-Plectomycetes (551 Ma), Candida-Saccharomyces (723 Ma), Hemiascomycetes-filamentous Ascomycota (982 Ma), Basidiomycota-Ascomycota (968 Ma), Mucorales-Basidiomycota (947 Ma), Fungi-Animalia (1,513 Ma), mosses-vascular plants (707 Ma), Chlorophyta-Tracheophyta (968 Ma), Rhodophyta-Chlorophyta+Embryophyta (1,428 Ma), Plantae-Animalia (1,609 Ma), Alveolata-plants+animals+fungi (1,973 Ma), Euglenozoa-plants+animals+fungi (1,961 Ma), and Giardia-plants+animals+fungi (2,309 Ma). By extrapolation, mitochondria arose approximately 2300-1800 Ma and plastids arose 1600-1500 Ma. Estimates of the maximum number of cell types of common ancestors, combined with divergence times, showed an increase from two cell types at 2500 Ma to ~10 types at 1500 Ma and 50 cell types at ~1000 Ma.
Conclusions
The results suggest that oxygen levels in the environment, and the ability of eukaryotes to extract energy from oxygen, as well as produce oxygen, were key factors in the rise of complex multicellular life. Mitochondria and organisms with more than 2–3 cell types appeared soon after the initial increase in oxygen levels at 2300 Ma. The addition of plastids at 1500 Ma, allowing eukaryotes to produce oxygen, preceded the major rise in complexity.
Similar content being viewed by others
Background
Organismal complexity can be defined in many ways, although the most common measure is the number of cell types [1–4]. Prokaryotes and many unicellular eukaryotes have only one or a few cell types, but vertebrates have more than 100 [1]. If cell types provide a tracer of complex life, it is of interest to know the general pattern of increase over the history of life. For example, a literal interpretation of the Cambrian explosion (520 million years ago, Ma), when many animal phyla first appeared in the fossil record, would be that a rapid increase in complexity occurred during the last one-ninth of the history of the planet. This apparent delay in the evolution of complex life on Earth has contributed to the argument that complex life may be rare in the universe [5]. Molecular clocks have yielded earlier times for the origin of animal phyla [6–9], but the methods have received criticism [10, 11]. At the same time, recent fossil discoveries have pushed back the origins of some groups of eukaryotes [12, 13], although a great discordance remains between most molecular clock results and the fossil record.
In this study, we have estimated a contour for the rise in complex life using a phylogeny and timescale derived from currently available protein sequence data. Ancestral numbers of cell types were estimated using the resulting phylogenetic and temporal framework. We have taken care to address criticisms of past molecular clock studies and have used all available timing methods applicable to protein sequence data, including global (constant rate) and local (variable rate) methods. The methods include those based on least-squares analysis [14], Bayesian inference [15], and penalized likelihood [16]. To avoid any potential artifacts arising from analysis of multiple alignments [17, 18], we have also used concatenated datasets [19]. We have tested our calibrations for reciprocity [20] and have used both vertebrate and non-vertebrate fossil calibrations and constraints. The results support a deep history for complex multicellular eukaryotes, and implicate oxygen as a possible trigger for the rise in complex life.
Results
Phylogenetic analyses
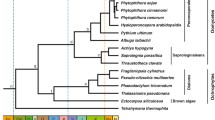
Our analyses of the concatenated data sets produced the following results: (i) animals are more closely related to fungi than to plants, (ii) red algae are closer to plants than to animals or fungi, (iii) choanoflagellates are closer to animals than to fungi or plants, (iv) diplomonads, euglenozoans, and alveolates each are basal to plants+animals+fungi, and (v) diplomonads are basal to other eukaryotes (including alveolates and euglenozoans) (Fig. 1). Most of these relationships are uncontroversial except for the uncertain position of the root of the tree as discussed elsewhere [21]. Our results with nuclear proteins agree with earlier ribosomal RNA trees [22] in supporting a root near the excavates (e.g., diplomonads) rather than on the opisthokont-amoebozoan branch (e.g., animals, fungi, and amoebas) [23]. Confidence values for these relationships were high (>99%) using three phylogenetic methods (maximum likelihood, minimum evolution, and Bayesian inference) in five of the seven analyses (Fig. 1). For the remaining two analyses (ii and v), significant support values were obtained with Bayesian inference, but varied for maximum likelihood and minimum evolution.
Phylogenetic relationships of selected eukaryotes. For each data set (column), all taxa are represented in all proteins. Support values are listed for the three methods (maximum likelihood, minimum evolution, Bayesian inference) and correspond to the node indicated by the arrow (and bolded group) for each tree.
Divergence times estimated with different methods
We estimated three deep (Precambrian) divergences in the eukaryote tree using the primary (bird-mammal) calibration and MGLLS (see Methods). In each case, there were no missing data; the data sets contained all proteins for all taxa. The divergence times were: vertebrate-arthropod (964 ± 132 Ma; 151 total and 120 rate constant proteins; 49,644 amino acids), animal-fungi (1492 ± 46 Ma; 188 total and 89 rate constant proteins; 31,362 amino acids), and animal-plant (1524 ± 53 Ma; 188 total and 143 rate constant proteins; 60,274 amino acids) (Table 1). These dates were similar to previous estimates using fewer proteins and different methods [8], and as secondary calibration points were found to be consistent in tests of reciprocity (see next section). In turn, these three time estimates were used as calibrations for estimating other divergence times using least-squares and penalized likelihood methods, and the 95% confidence intervals were used as nodal constraints for the Bayesian analysis. Rate parameters and a list of proteins used in the analyses are in supplemental tables 1, 2 (see Additional files 1–2).
The use of all available methods for timing protein sequence data (global and local clocks) and different methods of handling the data (multigene and supergene) resulted in remarkably similar estimates of divergence time (Table 1). On average, the six methods differed only 5.5 (4.6–6.4) % from the mean divergence time for a particular node. The resolution here of an animal-fungi relationship also revealed a faster rate of change (on average) in fungi that resulted in slightly younger (~16%) divergence times than reported previously [24]. We attribute the overall consistency among methods to the large size of the data sets and the use of rate tests to eliminate proteins showing substantial rate variation among taxa. It is known that all molecular clock methods, and especially local clock methods, perform best with the largest data sets [14–16], and greater differences are likely to be encountered when a small number of genes are used and when large rate differences are present.
Tests of the calibrations
We performed a "consistency test" [20] on our major secondary calibration of 964 Ma for the vertebrate-arthropod divergence to determine if it was consistent (reciprocally) with the primary calibration of 310 Ma; in this case, T1 (vertebrate-arthropod divergence) = 310 × (d(vertebrate-arthropod)/d(bird-mammal)) and T2 (bird-mammal divergence) = 964 × (d(bird-mammal)/d(vertebrate-arthropod)). Of 120 rate constant proteins, 118 (98.4%) showed T1 > T2, thus exhibiting high consistency. In the second half of the test, using the supergene matrix of the 82 rate constant proteins, we compared T2 (317 ± 29 Ma) with the primary calibration (310 Ma) and found it to be within one standard error, thus also showing high consistency. The other two secondary calibrations (animal-fungi and animal-plant) also were found to be consistent using the reciprocity test. For animal-fungi, 87/89 (97.8%) rate constant proteins were consistent with the vertebrate-arthropod divergence, and the corresponding T2 value (952 ± 56 Ma) was within one standard error of 964 Ma. For animal-plant, 132/143 (92.3%) rate constant proteins were consistent with the vertebrate-arthropod divergence, and the corresponding T2 value (989 ± 76 Ma) was within one standard error of 964 Ma.
To explore the effect of alternative fossil calibrations, we estimated the vertebrate-arthropod divergence time using our largest data set with expanded taxonomic representation (43 proteins, 19,183 amino acids, 8 taxa) and a diversity of vertebrate and non-vertebrate fossil constraints (lower bounds). The constraints were Drosophila-Anopheles (250 Ma), Homo-Mus (65 Ma), vertebrate-arthropod (540 Ma), Saccharomyces-Shizosaccharomyces (400 Ma) and animal-plant (1200 Ma) [12, 25, 26]. These constraints are less robust than the bird-mammal calibration (310 Ma), involve smaller numbers of proteins, and probably represent greater underestimates of the true divergence. Nonetheless, the Bayesian (SGLDT) and Penalized likelihood (SGLPL) methods yielded vertebrate-arthropod time estimates of 823 ± 167 and 1289 ± 206 Ma (respectively), still considerably predating the expected time (540 Ma) based on the animal fossil record. Eliminating the two vertebrate fossil constraints resulted in similar time estimates (816 ± 173 and 1285 ± 206 Ma, respectively).
Increase in cell types through time
The maximum cell types of organisms at different time periods are shown in Fig. 3, using data from living organisms and estimates of cell types in common ancestors (Table 2). The origin of life and divergence of archaebacteria and eubacteria were set at 4000 Ma and the origin of eukaryotes at 2700 Ma [27, 28], although earlier values for those events would not affect the overall trend, showing a baseline of about 2 cell types in prokaryotes. The results show an increase beginning about 2500 Ma to ~10 cell types at 2000 Ma, and then a second increase from 10–50 between 1500-1000 Ma (Fig. 3).
Discussion
Until the late Proterozoic (~600 Ma), oxygen levels remained low [29], probably limiting the size of eukaryotes, except in photosynthetic algae. However, such algae would not have occurred prior to the origin of plastids (approximately 1600-1500 Ma; Fig. 2) unless they acquired photosynthetic abilities through independent symbiotic events. This would argue against the interpretation of the older (>1600 Ma) fossils of "Grypania" as photosynthetic eukaryotic algae [30] and supports their interpretation as colonial prokaryotes [31].
A timescale of eukaryote evolution. The times for each node are taken from the summary times in Table 1, except for nodes 1 (310 Ma), 2 (360 Ma), 3 (450 Ma), and 4 (520 Ma), which are from the fossil record [25]; nodes 8 (1450 Ma) and 16 (1587 Ma) are phylogenetically constrained and are the midpoints between adjacent nodes. Nodes 12–14 were similar in time and therefore shown as a multifurcation at 1000 Ma; likewise, nodes 21–22 are shown as a multifurcation at 1967 Ma. The star indicates the occurrence of red algae in the fossil record at 1200 Ma, the oldest taxonomically identifiable eukaryote [12].
The most frequently used measure of organismal complexity has been the number of cell types [1, 2, 32]. Other possible measures were not deemed useful (e.g., organism size, genome size) or do not yet have sufficient data available from a diversity of eukaryotes (e.g., number of genes, proteins, transcription factors, introns/exons) for this analysis [32, 33]. With a refined timescale of eukaryote evolution it is possible to compare the increase in cell types through time with events in biotic and Earth history (Fig. 3). Although the specific pattern depends on the method of reconstructing character change, some general features are evident. Organisms with more than 2–3 cell types (the maximum in prokaryotes) appeared relatively early (~2000 Ma), soon after the surface environment became oxygenated at 2300 Ma (Great Oxidation Event; [34]). Later, cell types increased again, from 10 to at least 50 on the animal lineage (1500-1000 Ma). By the early Phanerozoic (500 Ma), organisms with more than 50 cell types had evolved. Complexity increased independently in fungi and plants, although at lower absolute levels than in animals.
Increase in the maximum number of cell types throughout the history of life. Data points at time zero are from living taxa [1–3, 50]; earlier data points were estimated with squared-change parsimony (solid circles) and linear parsimony (hollow circles) [51] using the molecular timetree (Fig. 2). The origin of life and divergence of archaebacteria and eubacteria were set at 4000 Ma and the origin of eukaryotes at 2700 Ma [27, 28], although earlier values for those events would not affect the overall trend. We follow McShea [4] in using maximum values at any given time and assuming that decreases do not occur. Dashed line shows an alternate (conservative) interpretation based on uncertainty as to the level of complexity of ancestors of early branching eukaryotes.
There is less confidence in ancestral cell type estimates in the period of initial increase (~2000 Ma) and better support for later estimates (1500-1000 Ma) because of knowledge of gene and structural homology among different groups of animals. For example, it is possible that the last common ancestor of alveolates and higher eukaryotes possessed only one or two cell types rather than the 7–8 predicted in this analysis (Fig. 3; 1973 ± 78 Ma), especially if the rise in complexity was delayed for some reason (e.g., origin of plastids). On the other hand, regardless of when the last common ancestor of protostomes and deuterostomes lived (976 ± 97 Ma in this analysis), there is no doubt that it was a relatively complex (not unicellular) organism with many cell types.
Some early branching eukaryotes (diplomonads) lack mitochondria, although it is debated as to whether they are primitively or secondarily amitochondriate [28]. However, the last common ancestor of mitochondriate eukaryotes, at 1967 ± 65 Ma (Fig. 2), must have possessed a mitochondrion. A molecular clock study of prokaryote and eukaryote genomes [35] arrived at a similar date (1840 ± 200 Ma) for the symbiotic event leading to the mitochondrion, using different data, methods, and approach. This may have been a key event in the rise of complex life, providing eukaryotes with 18 times more energy (over glycolysis alone) for cell signaling and other energy-requiring activities.
Conclusions
Prior to 2300 Ma, oxygen would not have been widely available for use as an energy source, even if mitochondria existed at that time. Therefore, the initial increase in complexity may have been a response to both energy availability (oxygen) and the ability to extract it (mitochondria). The second and more substantial increase in cell types (1500-1000 Ma) occurred immediately following the acquisition of the plastid (1600-1500 Ma) (Fig. 3), again suggesting a relationship with oxygen. Plastids provided eukaryotes with the ability to generate their own oxygen, benefiting those species (e.g., initially algae and alveolates) directly and their ecosystem partners (e.g., early animals and fungi) indirectly.
Methods
Data collection
Nuclear protein sequence data were obtained from the public databases (NCBI Entrez: http://www.ncbi.nlm.nih.gov/entrez/) for all species relevant to each taxonomic comparison, calibration taxa, and outgroups for rate testing (supplemental Table 2; see Additional file 2). Initial datasets were screened for orthology using reciprocal BLAST best hits and manual tree building. Additional sequences were also generated from the demosponge, Microciona prolifera, for two proteins (enolase and pyruvate kinase). Total messenger RNA was extracted and converted to cDNA pools using reverse transcriptase PCR. Primers were designed from protein sequences available in the public database (enolase forward: 5' TCCCGYGGKAAYCCMACHGTKGAGGT 3', reverse: 5' GGKAGRATCATRAAYTCYTGCATRGC 3'; pyruvate kinase forward: 5' TTCTCYCAYGGMWCSYACGAGTAYCA 3', reverse: 5' CGRAYRAAMGARGCRAASAYCATGTC 3'). Sequences were aligned [36] and regions of ambiguous alignment were removed when necessary. Neighbor-joining trees were constructed (Poisson model) [37] and sequences presumed to be non-orthologous, due to extensive rate variation and evidence of gene duplication, were excluded from further analyses. Short (<100 amino acids) sequences were omitted.
Phylogenetic analyses
We used a consensus phylogenetic framework based on a diversity of molecular and morphological studies [21, 28]. We also tested six phylogenetic questions with our large protein alignments. The data sets ranged in size from six proteins (3195 amino acids) in the choanoflagellate set to 151 proteins (75,287 amino acids) in the animal-fungi set. All data sets were complete in that they contained all proteins for all species. These concatenated datasets were analyzed using maximum likelihood (JTT + gamma model, quartet puzzling with 1000 steps) [38], minimum evolution (Neighbor-joining, Poisson + gamma model, 2000 bootstraps, complete deletion) [37], and Bayesian Inference (JTT + gamma model, 50,000 generations, 4 chains with starting temp = 0.2) [39]. The shape parameters of the gamma distribution for the different phylogenetic data sets, estimated from the data [40] were: Giardia (α = 1.12), euglenozoans (α = 1.23), alveolates (α = 1.18), multiprotist (Giardia, euglenozoans, alveolates, plants, animals, fungi) (α = 0.93), animal+fungi (α = 1.198), plants+red algae (α = 0.85), and animals+choanoflagellates (α = 0.865).
Calibrations
Times of divergence derived from the fossil record are always underestimates of the true divergence [11, 41]. Even the 1200 Ma date for fossil red algae [12] is considered to be an underestimate of the origin of that group because it represents a rare preservation event, hundreds of millions of years older than the next oldest fossil red algae. Therefore, care must be exercised in selecting calibration points or constraints from the fossil record for molecular clock analysis or else they may, in turn, result in considerable underestimates of divergence time [28]. The divergence of the lineages leading to birds and mammals in the fossil record (310 Ma) provides an unusually well-constrained calibration point and permits large numbers of proteins to be used [14]. A more conservative estimate of 288 Ma [42] was used as the lower bound for the mammal-bird divergence in the Bayesian and penalized likelihood analyses; the upper bound was defined by the presence of stem amniotes in the Mid-Late Visean (~345 Ma) [43]. With this primary calibration, we estimated three deeper divergences in the eukaryote tree. In turn, they provided Precambrian calibration points for estimating other divergences. Well-constrained fossil calibration points were otherwise unavailable for the Precambrian. Secondary calibrations minimize the difference between the calibration point and the divergence to be timed, thereby increasing the number of applicable genes and the overall precision of time estimates. For example, genes that show a difference of more than one or two substitutions in a young calibration event (e.g., between two mammals) usually will be evolving too quickly to be alignable or useful for timing deep divergences in eukaryotes. Also, large extrapolations can exaggerate any biases that might exist. Therefore, establishing anchor points or secondary calibrations in the Precambrian permits more genes to be used and reduces the biases caused by large extrapolations.
Divergence time estimation
Because the coefficient of variation of time estimates is large for small numbers of genes [14], we used a minimum of 20 genes for each divergence. We chose eighteen divergences among major lineages of eukaryotes, including some analyzed previously [24]. To increase the number of genes available for early branching animals, we sequenced the cDNAs of two genes (enolase and pyruvate kinase) in a poriferan (Microciona prolifera) and added those to the assembled data. We subjected all data to global (constant rate) and local (rate variation among lineages) clock methods, including Multigene Global Least Squares (MGGLS) [14], Multigene Local Least Squares (MGLLS) [44], Supergene Global Least Squares (SGGLS) [17], Supergene Local Least Squares (SGLLS), Supergene Local Divtime (SGLDT) [15], and Supergene Local Penalized Likelihood (SGLPL) [16]. The first four (least squares) methods are distance based, SGLDT is a Bayesian method, and SGLPL is a semi-parametric likelihood method. Multigene methods treat each gene separately whereas supergene methods use concatenations of genes [19, 41].
All proteins were tested for rate constancy [45, 46]; those rejected at the 5% significance level were excluded from timing analyses. Gene-specific and supergene gamma shape parameters (α) were calculated [40] and used for distance and time estimation [45]. For MGGLS, MGLLS, SGGLS, and SGLLS methods, gene- or supergene-specific rates of sequence change were estimated using linear regression (y-intercept fixed through the origin) from one or more calibrations and applied to the intergroup distance estimates to produce gene- or supergene-specific times. The mode was used as the measure of central tendency in the multigene analyses due to the sensitivity of the mean to extreme values [47]; standard errors of the mode were obtained with bootstrapping (10,000 replications); outliers were trimmed for the supergene data sets.
The SGLDT method was performed using Divtime5b [15]; maximum likelihood branch lengths were calculated under a JTT model using an accompanying program, ESTBRANCHES. The means of the prior distributions ("priors") for the rate parameter and the root time (rt and t, respectively) were calculated for each dataset (see Supplemental Table 1 for parameters). Calibration nodes were constrained using the 95% confidence interval of the secondary calibrations (as discussed previously). Divergence time "posteriors" and their 95% credibility intervals were recorded for each dataset. The SGLPL method was performed in R8S version 1.6 [48] with maximum likelihood branch lengths calculated under a PC+gamma model [40]. A cross-validation procedure [16] was used to obtain the optimal smoothing parameter for each dataset. One hundred bootstrapped datasets were generated to obtain the mean and error on divergence time estimates for each dataset [40, 49]. While it is possible to constrain nodes using penalized likelihood, we found that the use of constraints forced the method to overestimate extrapolations and underestimate interpolations (data not shown). For this reason we chose to use fixed calibrations to estimate divergence times with penalized likelihood.
Estimation of ancestral numbers of cell types
The maximum numbers of cell types in major groups of living organisms were obtained from the literature [1–3, 50]: Mammalia (120), Reptilia (120), Amphibia (120), Actinopterygii (120), Arthropoda (69), Agnatha (67), vascular plants (44), mosses (26), Cnidaria (22), Porifera (16), red algae (14), alveolates (14), Pyrenomycetes (9), Hymenomycetes (9), Plectomycetes (9), chlorophytes (5), Saccharomyces (3), Mucorales/Blastocladiales (3), amoebozoans (3), Candida (2), Choanoflagellata (2), Euglenozoans (2), diplomonads (2), eubacteria (2), archaebacteria (2), and Archiascomycetes (1). These were used to estimate the maximum number of cell types of common ancestors. This was accomplished with linear and squared change parsimony [51] and the phylogenetic relationships of the groups. Linear and squared change parsimony are preferred over other more complicated methods when all species are extant (as they must be here, for accurate counts of cell types) [52]. Linear parsimony yields more conservative (in this case, lower) estimates than squared change parsimony when a trend is present. For some nodes, linear parsimony yields a range of values; in those cases we followed Webster and Purvis [52] in using the midpoint of the range. The two multifurcations in Fig. 2 were used with squared-change parsimony. Linear parsimony cannot be used with multifurcations and therefore the fungal multifurcation was resolved as (Mucorales/Blastocladiales (Hymenomycetes (Archiascomycetes ((Candida, Saccharomyces), (Plectomycetes, Pyrenomycetes))))) and the basal protist multifurcation was resolved as (Diplomonads (Euglenozoans (Alveolates, other eukaryotes))); alternative resolutions did not affect the trend in cell type number.
References
Bonner JT: The evolution of complexity by means of natural selection. 1988, Princeton, New Jersey, Princeton University Press
Valentine JW, Collins AG, Meyer CP: Morphological complexity increase in metazoans. Paleobiology. 1994, 20: 131-142.
Bell G, Mooers AO: Size and complexity among multicellular organisms. Biological Journal of the Linnean Society. 1997, 60: 345-363. 10.1006/bijl.1996.0108.
McShea DW: The hierarchical structure of organisms: a scale and documentation of a trend in the maximum. Paleobiology. 2001, 27: 405-423.
Ward PD, Brownlee D: Rare Earth. 2000, New York, Copernicus, 333-
Wray GA, Levinton JS, Shapiro LH: Molecular evidence for deep Precambrian divergences among metazoan phyla. Science. 1996, 274: 568-573. 10.1126/science.274.5287.568.
Gu Xun: Early metazoan divergence was about 830 million years ago. Journal of Molecular Evolution. 1998, 47: 369-371.
Wang DY, Kumar S, Hedges SB: Divergence time estimates for the early history of animal phyla and the origin of plants, animals and fungi. Proceedings of the Royal Society of London Series B-Biological Sciences. 1999, 266: 163-171. 10.1098/rspb.1999.0617.
Runnegar B: A molecular-clock date for the origin of the animal phyla. Lethaia. 1982, 15: 199-205.
Ayala FJ, Rzhetsky A, Ayala FJ: Origin of the metazoan phyla: molecular clocks confirm paleontological estimates. Proceedings of the National Academy of Sciences (U.S.A.). 1998, 95: 606-611. 10.1073/pnas.95.2.606.
Benton MJ, Ayala FJ: Dating the tree of life. Science. 2003, 300: 1698-1700. 10.1126/science.1077795.
Butterfield NJ: Bangiomorpha pubescens n. gen., n. sp.: implications for the evolution of sex, multicellularity, and the Mesoproterozoic/Neoproterozoic radiation of eukaryotes. Paleobiology. 2000, 26: 386-404.
Javaux EJ, Knoll AH, Walter MR: Morphological and ecological complexity in early eukaryotic ecosystems. Nature. 2001, 412: 66-69. 10.1038/35083562.
Kumar S, Hedges SB: A molecular timescale for vertebrate evolution. Nature. 1998, 392: 917-920. 10.1038/31927.
Kishino H, Thorne JL, Bruno WJ: Performance of a divergence time estimation method under a probabilistic model of rate evolution. Molecular Biology and Evolution. 2001, 18: 352-361.
Sanderson MJ: Estimating absolute rates of molecular evolution and divergence times: a penalized likelihood approach. Molecular Biology and Evolution. 2002, 19: 101-109.
Nei M, Xu P, Glazko G: Estimation of divergence times from multiprotein sequences for a few mammalian species and several distantly related organisms. Proceedings of the National Academy of Sciences (U.S.A.). 2001, 98: 2497-2502. 10.1073/pnas.051611498.
Rodriguez-Trelles F, Tarrio R, Ayala FJ: A methodological bias toward overestimation of molecular evolutionary time scales. Proceedings of the National Academy of Sciences (U.S.A.). 2002, 99: 8112-8115. 10.1073/pnas.122231299.
Hedges SB, Kumar S: Genomic clocks and evolutionary timescales. Trends in Genetics. 2003, 19: 200-206. 10.1016/S0168-9525(03)00053-2.
Shaul S, Graur D: Playing chicken (Gallus gallus): methodological inconsistencies of molecular divergence date estimates due to secondary calibration points. Gene. 2002, 300: 59-61. 10.1016/S0378-1119(02)00851-X.
Baldauf SL: The deep roots of eukaryotes. Science. 2003, 300: 1703-1706. 10.1126/science.1085544.
Sogin ML: History assignment: when was the mitochondrion founded?. Current Opinion in Genetics and Development. 1997, 7: 792-799. 10.1016/S0959-437X(97)80042-1.
Stechmann A, Cavalier-Smith T: Rooting the eukaryote tree by using a derived gene fusion. Science. 2002, 297: 89-91. 10.1126/science.1071196.
Heckman DS, Geiser DM, Eidell BR, Stauffer RL, Kardos NL, Hedges SB: Molecular evidence for the early colonization of land by fungi and plants. Science. 2001, 293: 1129-1133. 10.1126/science.1061457.
Benton MJ: The Fossil Record 2. 1993, London, Chapman and Hall, 845-1
Taylor TN, Hass H, Kerp H: The oldest fossil ascomycetes. Nature. 1999, 399: 648-10.1038/21349.
Feng D-F, Cho G, Doolittle RF: Determining divergence times with a protein clock: update and reevaluation. Proceedings of the National Academy of Sciences (U.S.A.). 1997, 94: 13028-13033. 10.1073/pnas.94.24.13028.
Hedges SB: The origin and evolution of model organisms. Nature Reviews Genetics. 2002, 3: 838-849. 10.1038/nrg929.
Knoll Andrew H., Carroll Sean B.: Early Animal Evolution: Emerging Views from Comparative Biology and Geology. Science. 1999, 284: 2129-2137. 10.1126/science.284.5423.2129.
Han T-M, Runnegar B: Megascopic eukaryotic algae from the 2.1 billion-year-old Negaunee iron-formation, Michigan. Science. 1992, 257: 232-235.
Samuelsson J, Butterfield NJ: Neoproterozoic fossils from the Franklin Mountains, northwestern Canada: stratigraphic and paleobiological implications. Precambrian Research. 2001, 107: 235-251. 10.1016/S0301-9268(00)00142-X.
Carroll SB: Chance and necessity: the evolution of morphological complexity and diversity. Nature. 2001, 409: 1102-1109. 10.1038/35059227.
Szathmary E, Jordan F, Pal C: Molecular biology and evolution. Can genes explain biological complexity?. Science. 2001, 292: 1315-1316. 10.1126/science.1060852.
Holland HD: Volcanic gases, black smokers, and the Great Oxidation Event. Geochimica et Cosmochimica Acta. 2002, 21: 3811-3826. 10.1016/S0016-7037(02)00950-X.
Hedges SB, Chen H, Kumar S, Wang D-Y, Thompson AS, Watanabe H: A genomic timescale for the origin of eukaryotes. BMC Evolutionary Biology. 2001, 1: 4-10.1186/1471-2148-1-4.
Thompson JD, Higgins DG, Gibson TJ: CLUSTALW: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Research. 1994, 22: 4673-4680.
Kumar S, Tamura K, Jakobsen I, Nei M: MEGA: Molecular Evolutionary Genetics Analysis 2.0. 2000, Tempe, Arizona, Arizona State University
Strimmer K, vonHaeseler A: Quartet puzzling: A quartet maximum-likelihood method for reconstructing tree topologies. Molecular Biology and Evolution. 1996, 13: 964-969.
Huelsenbeck J, Ronquist F: MrBayes Version 3.0. 2003, Uppsala, Sweden, Evolutionary Biology Centre, Uppsala University
Yang Z: PAML: a program package for phylogenetic analysis by maximum likelihood. CABIOS. 1997, 13: 555-556.
Wray GA: Dating branches on the tree of life using DNA. Genome Biology. 2001, 3: 1-7. 10.1186/gb-2001-3-1-reviews0001.
Lee MSY: Molecular clock calibrations and metazoan divergence times. Journal of Molecular Evolution. 1999, 49: 385-391.
Paton RL, Smithson TR, Clack JA: An amniote-like skeleton from the early Carboniferous of Scotland. Nature. 1999, 398: 508-513. 10.1038/19071.
Schubart Christoph D., Diesel Rudolf, Hedges S. Blair: Rapid evolution to terrestrial life in Jamaican crabs. Nature. 1998, 393: 363-365. 10.1038/30724.
Kumar S: Phyltest: a program for testing phylogenetic hypotheses, ed. 2.0. Institute of Molecular Evolutionary Genetics. 1996, University Park, PA, Pennsylvania State University
Takezaki Nauko, Rzhetsky Andrey, Nei Masatoshi: Phylogenetic test of the molecular clock and linearized trees. Molecular Biology and Evolution. 1995, 12: 823-833.
Hedges SB, Shah P: Comparison of mode estimation methods and application in molecular clock analysis. BMC Bioinformatics. 2003, 4: 31-10.1186/1471-2105-4-31.
Sanderson MJ: r8s: inferring absolute rates of molecular evolution and divergence times in the absence of a molecular clock. Bioinformatics. 2003, 19: 301-302. 10.1093/bioinformatics/19.2.301.
Felsenstein J: PHYLIP version 3.6. 2002, Seattle, Department of Genetics, University of Washington
Margulis L, Corliss JO, Melkonian M, Chapman DJ: Handbook of Protoctista. 1990, Boston, Massachusetts, Jones and Bartlett, 914-
Maddison WP, Maddison DR: MacClade. 1992, Sunderland, MA, Sinauer Associates
Webster AJ, Purvis A: Testing the accuracy of methods for reconstructing ancestral states of continuous characters. P Roy Soc Lond B Bio. 2002, 269: 143-149. 10.1098/rspb.2001.1873.
Acknowledgements
We thank D. Boone, B. Eidell, J. Hughes, M. Lyons-Weiler, L. Poling, P. Shah, and H. Stone for assistance in the laboratory; J. Hines for artwork; and D. Pisani and J. L. Thorne for discussion. JLS was supported by the Beckman Scholars Program. Other funding was provided by grants to SBH from the National Aeronautics and Space Administration (Astrobiology Institute; NCC2-1057 and NNA04CC06A) and National Science Foundation (DBI-0112670).
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
SBH directed the research and drafted the manuscript. JEB carried out the bioinformatics research and timing analyses. MLV and JLS assisted in data collection and analysis, and JLS collected new sequences from Microciona.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Hedges, S.B., Blair, J.E., Venturi, M.L. et al. A molecular timescale of eukaryote evolution and the rise of complex multicellular life. BMC Evol Biol 4, 2 (2004). https://doi.org/10.1186/1471-2148-4-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2148-4-2