Abstract
Background
Developing reliable and efficient strategies allowing to infer a function to yet uncharacterized proteins based on interaction networks is of crucial interest in the current context of high-throughput data generation. In this paper, we develop a new algorithm for clustering vertices of a protein-protein interaction network using a density function, providing disjoint classes.
Results
Applied to the yeast interaction network, the classes obtained appear to be biological significant. The partitions are then used to make functional predictions for uncharacterized yeast proteins, using an annotation procedure that takes into account the binary interactions between proteins inside the classes. We show that this procedure is able to enhance the performances with respect to previous approaches. Finally, we propose a new annotation for 37 previously uncharacterized yeast proteins.
Conclusion
We believe that our results represent a significant improvement for the inference of cellular functions, that can be applied to other organism as well as to other type of interaction graph, such as genetic interactions.
Similar content being viewed by others
Background
While more data become available, analyzing protein-protein interaction (PPI) networks appears as a particularly effective way to make functional predictions for proteins of unknown function. Most studies so far focused on the baker's yeast S. cerevisiae due to large available datasets [1, 2], but recent experimental data for D. melanogaster [3] will most probably broaden the field of investigations. It is therefore of crucial interest to develop reliable and efficient strategies allowing to infer a function to yet uncharacterized proteins based on interaction data.
It was soon noticed that proteins of similar cellular functions tend to lie within a short distance in the interaction graph. Based on this property, Schwikowski et al. [4] proposed a prediction method in which a protein of unknown function is assigned the three most frequent cellular functions represented among its direct interaction partners. This approach is strictly local, as it does not take into account the graph as a whole but only the immediate protein neighborhood. However, we have good reasons to believe that the organization of proteins inside the interactome goes beyond the one-step separation. Protein complexes and pathways are an example of more complicated relationships between proteins involved in a same biological process. Indeed, other methods focused on the fact that proteins sharing a significant number of interaction partners are likely to participate in common cellular processes as proposed by Jacq (2001). Recently, we have designed PRODISTIN [5, 6], a method in which distance values between all protein pairs are computed from the number of common and specific interaction partners and used to build a classification tree. Functional classes are defined according to the tree topology and to the number of proteins sharing functional annotations. The functional predictions for yet uncharacterized proteins are then proposed based on their belonging to a particular functional class. An alternative method for predicting biological functions was proposed [7], which ranks protein pairs according to their probability for having the experimentally measured number of common interaction partners. A different method, which does not rely on common interaction partners was suggested by Vasquez et al. [8]; it optimizes the annotations of uncharacterized proteins such as to minimize the number of interactions between proteins of different functional groups. These latter two approaches, while based on the interaction network, do not define any clusters of proteins. Biological knowledge teaches us that dense protein-protein interactions are the sign of the common involvement of those proteins in certain biological processes. We therefore tried to select dense classes of proteins sharing a high percentage of interactions in the interaction graph. Several clustering algorithms applied to protein interaction graphs have been proposed so far [9, 10]. They are based on a density function evaluated in each vertex x which is computed from the number of edges in its neighborhood. We adopted another approach, computing first an appropriate distance between vertices. Generally the length of a shortest path or the Czekanowski-Dice distance are used, and a classical clustering method is then applied [6, 11]. We will present an alternative algorithm using the Czekanowski-Dice distance as in [6]. From the distance matrix, a new graph Γ is built, which is then partitioned into disjoint classes of proteins using an appropriate density function. Our algorithm differs from similar approaches in many ways : 1) the graph Γ is not a classical threshold graph, in which edges are selected when their length is lower than a threshold value, and 2) we use the valuation of the edges to measure a density in each vertex and 3) we perform progressive clustering.
The resulting classes are assigned a biological function according to the functional annotations of their members following a classical majority rule. Finally, a refined annotation procedure is proposed to predict the cellular function(s) of uncharacterized proteins, taking into account the function(s) assigned to the class and the direct interaction partners of uncharacterized protein present within the class. Hence, interaction data is used at two levels (see figure 1): first to define the classes using our partitioning algorithm, but also to annotate uncharacterized proteins once the classes have been formed. Overall, the quality of the prediction will strongly depend on (a) the validity of the clustering algorithm which must reflect the biological reality, and (b) the annotation procedure within classes.
Flowchart of the method. (a) A graph is built from a list of binary protein-protein interactions. (b) The Czekanowski-Dice distance is calculated among all pairs of proteins. (c) A graph Γ is build based on distance values (see text for details). (d) Classes are constructed after computing a density function De. (e) Classes are functionally annotated according to a threshold majority rule in classes (MRC). (f) Function are predicted for uncharacterized proteins by a next neighbor exploration.
Results
Graph, classes and partitions
We analyze the interaction network as a graph, such that proteins are the vertices and each interaction is an undirected edge. Our aim is to build clusters of proteins sharing a high percentage of interactions, as this appears to be a strong indicator of biological relatedness. We use the Czekanowski-Dice distance. D, because it increases the weight of shared interactors, and because two proteins having no common interactors will get the maximum distance value, while those interacting with exactly the same set of proteins will have zero value:

in which i and j denote two proteins, Int(i) and Int(j) are the lists of their interactors plus themselves (to decrease the distance between proteins interacting with each other) and Δ is the symmetrical difference between the two sets. From the distance matrix, we first build another valued graph Γ = (X, E), then we evaluate a density function De in each vertex to perform clustering only from Γ and De.
Graph
Given a distance matrix, D : X × X →  , the first operation is to select a degree δ which works as a threshold. From any element x, the distance values D(x,y) are ranked in increasing order and the δ-th value gives the σ
x
threshold. Then, we take as edges in E all the pairs (x,y) such that D(x,y) ≤ σ
x
. Let n = |X|, m = |E| and Γδ = (X, E) be the corresponding graph. It is not a classical threshold graph on D, since the threshold value is not the same for all the vertices.
, the first operation is to select a degree δ which works as a threshold. From any element x, the distance values D(x,y) are ranked in increasing order and the δ-th value gives the σ
x
threshold. Then, we take as edges in E all the pairs (x,y) such that D(x,y) ≤ σ
x
. Let n = |X|, m = |E| and Γδ = (X, E) be the corresponding graph. It is not a classical threshold graph on D, since the threshold value is not the same for all the vertices.
Moreover, it is not a regular graph with degree δ either, because the edge selection process is not symmetrical. Consequently, there can be more than δ vertices incident to x.
When there is no ambiguity on the δ value, the graph will simply be denoted Γ. For any part Y of X, let Γ (Y) be the set of vertices not in Y that are adjacent to Y. Thus, the neighborhood of x is denoted Γ (x), the degree of a vertex x is Dg(x) = |Γ (x)|.
Density function
For each vertex x, we compute a density value denoted De(x) which would be high when the elements of Γ (x) are close to x. Let Dmax be the largest distance value. We evaluate a density function computed from the average length of the edges from x.

Using the distance values gives a much precise density than the simple number or the percentage of triangles or edges in the neighborhood of any vertex. The dense classes are by definition connected parts in Γ sharing high density values. Our initial idea was to search for a density threshold and to consider the partial subgraph whose vertices have a density greater than this threshold. Classes would have been the connected components. This strategy does not give the expected results. Enumerating all the possible threshold values, we have observed that often none was satisfying. By decreasing the threshold, we often obtain only a single growing class, and many singletons. Since there is no straightforward way to fix a threshold, the local maximum values of the density function are considered.
Classes at three levels
We construct classes in three steps :
-
we first build a kernel which is a connected part of the vertices for which the density is locally maximum and greater than the average;
-
then, these classes are extended, adding vertices that are connected to only one kernel ;
-
finally the unclassified elements are assigned to one of the previous classes.
Kernels
a kernel, denoted K, is a connected part of Γ, obtained by the following algorithm : we first search for the local maximum values of the density function and we consider the partial subgraph of Γ reduced to these vertices.
∀ x ∈ K, ∀ y ∈ Γ (x) we have De(x) ≥ De(y).
The initial kernels are the connected components of this graph. More precisely, if several vertices with maximum value are in the same kernel, they necessary have the same density value ; otherwise the initial kernels are singletons. Then, we assign recursively to each kernel K the vertices (i) having a density greater than or equal to the average density value over X and (ii) that are adjacent to only one kernel. Doing so, we avoid any ambiguity in the assignment, postponing the decision when several are possible.
The number of kernels is the number of classes and it remains unchanged in the following. Therefore, the number of classes is not an input parameter as for most alternative clustering methods optimizing a criterion. We shall see that it performs well, when there is a small number of classes, having from 30 to 50 elements.
Extended classes
at the second level, we assign elements that are connected to a unique kernel, whatever their density is. If an element which is not in a kernel is connected to several ones, the decision is again postponed.
Complete classes
finally, to get partitions, we assign the remaining elements to one class. For x and any extended class C to which it is connected, we compute the number of edges between x and C, and also its average distance value to C. Finally there are two candidates, the majority connected class C
m
and the closest one C
d
. If they are identical, x is connected to it. And if they are different we apply the empiric following rule : if  > 1.5, class C
m
is retained, because the number of links to C
m
is clearly larger than to C
d
; otherwise C
d
is retained.
> 1.5, class C
m
is retained, because the number of links to C
m
is clearly larger than to C
d
; otherwise C
d
is retained.
Validation of the method
We want to assess that this partitioning method is able to detect areas in a graph having a percentage of edges larger than the average over the whole graph. Starting with a graph containing a certain number of known classes, the two main points to verify are the ability to recover the correct number of classes and the degree of identity between the predicted and the initial classes. In order to do so, we have developed a random graph generator in which some balanced classes are established. We do not pretend to mimic protein interaction networks which have a power-law degree distribution. Graphs are built selecting at random edges with a probability p i if its two ends are in the same class and p e if they are in two different classes. To evaluate the class fitting, we use the same parameters as in Guénoche (2004).
-
τ e , the percentage of elements in one recovered class coming from its corresponding class in the initial partition;
-
τ p , the percentage of pairs in the same class that are also joined together in the initial partition.
We have generated 200 distances on 200 vertices distributed in 5 classes, setting first p i = .5 and p e = .1 and secondly p i = .4 and p e = .1. For δ = 20 (10% of the number of vertices) we obtain the best results :
-
in the first case, we get 5 classes in 67% of the trials, and a number of classes in the range 4–6 in 97% ; the criteria values are τ e = .97 and τ p = .94 ;
-
in the second case the percentage are respectively 51 and 92 ; the criteria values are τ e = .86 and τ p = .76
These average results prove that this clustering method is able to recover classes in a graph in which some parts have a higher density of edges. The larger the density gap, the more accurate the prediction of the number of classes. Hence, it seems appropriate to apply this clustering algorithm to protein interaction networks, in which the density of edges is not uniform.
Complexity
To establish graph Γ, it is necessary to order the distance values from any x. The computation of σ x is in O(n log n) and the selection of the edges is in O(n). Finally, the graph construction is in O(n2 log n).
To evaluate De(x) it is sufficient to test the edges in the neighborhood of x which contains at most n vertices. The computation of the density function is thus in O(n2).
Kernel computation is in O(n2) to find the local maximum vertices, and in O(m)= O(n2) to determine the kernel elements. During the following steps, for any x we count its connections to the kernels, and then to the extended classes. Both are also in O(n2). Finally, the complexity of the clustering method is O(n2 log n).
Using classes for functional annotation of proteins
We apply the clustering algorithm described above to the network of protein-protein interactions in yeast. In order to assess the efficiency of our method and confront it with others, we use a curated dataset (as described in Brun et al., 2003) of 2097 protein-protein interactions between 876 yeast proteins, all involved in at least 3 binary interactions. We choose to rule out poorly connected proteins from the graph because the existence of false-positive and false-negative interactions weights more for such proteins. The functional annotations used to assign the class annotation and predict protein function are those of the Yeast Protein Database (YPD, 1st June 2002), which have been manually updated. This means that for proteins annotated as "unknown" at the time the database became commercial, we have checked in the Saccharomyces Genome Database (SGD, February 3rd, 2004) whether it had received a Gene Ontology (GO) annotation in the meantime, and if so, we converted the GO annotation to its corresponding YPD keyword. We choose δ = 2, which leads to a partition of the graph in 126 classes [see additional file 1].
Biological coherence of classes
By comparing the classes obtained with those built using the PRODISTIN method (Brun et al., 2003), we found that 42 out of 126 are equal or included in PRODISTIN classes, and 70/126 have at least 70% overlap. This is quite remarkable and confirms the biological significance of the method, since PRODISTIN classes are by definition functionally homogeneous clusters (at least 50% of proteins in a PRODISTIN class have a common annotation). In addition, a detailed analysis of the 14 classes that only share 1 protein or do not overlap at all with PRODISTIN classes, showed that some of them are highly biologically significant. For instance, the three proteins Csm3, Tofl and Top1, which form a class, are all important in maintaining the integrity of the chromosome and form a class. Similarly, Bspl, Capl and Cap2, which also form a class, are all parts of the actin cytoskeleton. Finally, the class containing Pcl2, Pho85, Psy2, Sorl and Sor2 underlines the pleiotropic functions of Pho85. This cyclin-dependent protein kinase is involved in cell cycle control (when interacting with Pcl2, for instance) but also in the regulation of the accumulation of glycogen, a major polysaccharide storage form of glucose in yeast [12]. This is thus explaining the clustering of these two last proteins with Sorl and Sor2 which both participate to glucose metabolism. Interestingly, Psy2 is a protein of unknown function, which was recently related to proteins involved in the progression of the cell cycle [13]. Its partitioning in this particular class thus reinforces this recent experimental result and illustrates the adequacy of our method. Therefore, the method appears to not only group proteins involved in the same cellular processes but also to underline crosstalk between cellular processes. The protein classes built by the algorithm being biologically significant, we thus choose to assign them a functional annotation corresponding to the functions shared by at least 50% of the annotated proteins of the class.
A new annotation procedure for uncharacterized proteins
As already mentioned in the introduction, a popular annotation procedure for single uncharacterized proteins, once clusters of proteins are available, is the simple majority rule: the most frequent function, or those shared by more than d% of the annotated proteins in the class are assigned to proteins of unknown functions in the class. We will call this approach the "majority rule in class" approach, or MRC for short. The PRODISTIN method proposed in [6] is an example of the MRC approach, in which the threshold d is fixed to 50%. However, it is applied to different classes than those obtained with the previously described clustering algorithm.
An alternative solution was proposed by Schwikowski et al. [4], which relies directly on the interaction graph (i.e. regardless of any clustering). The idea is to assign to a protein of interest the most frequent (e.g. 3) functions of its direct interaction partners ("majority rule among neighbors", or MRN).
Although these approaches can yield satisfactory results in particular cases, there is certainly room for improvement. For instance, the MRN procedure is strictly local and ignores neighbors that are more than one step away from the protein of interest. This is probably a too restrictive representation of how proteins work together.
The procedure we propose in this paper is a simple improvement, which aims at (partly) resolving the problems of previous procedures discussed so far while combining their respective advantages. We will call it " hybrid method", as it is mainly based on protein classes extracted as described in the previous section from the interaction network, but also takes into account the interaction partners of each protein inside its class. Using classes means taking into account the relationship between proteins that are close to each other though not directly interacting, while looking at the direct interaction partners allows to refine the predictions by using local relationships. More precisely, our procedure for predicting functions consists of three steps:
-
1.
for a given class, as explain in the previous paragraph, we list all functions found among proteins in the class, and keep only those that are shared by at least d% of the annotated proteins of the class (d = 50 in our experiment): we call this set of annotations f g ;
-
2.
for a given protein P inside a class, we list the functions found among proteins in its class with which it interacts directly: this second set of functions is called f n ;
-
3.
the predicted annotations for P are (if any) those in f g ∩ f n .
A prediction is possible as soon as the intersection is not empty. This means that there should exist one or several functions that are frequently encountered among proteins in a class (f g ≠ Ø), but also that single proteins have annotated interaction partners (f n ≠ Ø). This double filtering-allows to lower the threshold d with respect to the MRC method, without increasing the rate of false positives. Moreover, the lower the threshold, the more proteins we can make predictions for (Fig. 2).
Function prediction for uncharacterized proteins
As mentioned earlier, the parameter d varies between 30 and 70%. A conservative choice of d = 70% leads to a prediction for 20 previously uncharacterized proteins (TFR = 44%, RCP = 75%) while at d = 30%, we make a prediction for 48 proteins (TFR = 51%, RCP = 53%). We choose d = 50%, which yields a prediction for 37 proteins which had no defined cellular role in SGD (February 3rd, 2003).
Our predictions (Table 1) are then compared with recent experimental results described in the literature, annotated in Gene Ontology and reported in the Saccharomyces Genome Database (SGD, march 15th 2004) http://www.yeastgenome.org/. Novel annotations are available for 12 out of the 37 proteins. For 8 of them (67%), our predictions are in accordance with or related to the experimental results. For the 4 other proteins (33%), our predictions disagree (Table 2). Overall, these observations strengthen the relevance of our method.
Comparison with other procedures
Here, we compare the hybrid method to other annotation procedures, in particular the MRC approach, the MRN approach and the general optimization method (GOM) proposed by Vazquez et al. [8]. The comparison with previously published methods is made difficult by the fact that it has been applied to different datasets, and cannot be implemented easily to be run on our data. We have implemented the MRC and MRN algorithm, which we applied to our interaction network in order to achieve a direct comparison with our procedure. As for the GOM, we have tried to confront the functional predictions made for uncharacterized proteins and to use newly available annotation evidence to validate both prediction methods. This will be discussed at the end of this section.
We defined two criteria reflecting the efficiency of the prediction method
-
the rate of true functions recovered (TFR): this indicator is determined by the "leave-one-out" method, i.e. by successively scanning all annotated proteins in a class and confronting their true annotations with the predicted ones,
-
the rate of correct predictions (RCP), i.e. the number of correct predictions over the total number of predictions made.
For our method and the MRC approach, these indicators depend on the threshold d. A reasonable interval for d is [30, 70]: below 30%, a function is not particularly representative whereas above 70%, the threshold is too stringent and yields too few predictions. For a given value of d, our procedure predicts a function for less proteins than the simple MRC, due to the additional step in the method. Hence, in order to compare both approaches, we shall plot both criteria against the number of proteins for which a prediction is made (out of the total number of proteins, hence 876). The results are shown in Fig. 3.
Comparison of our procedure (full squares) and the MRC strategy (full diamonds) of the rate of true functions recovered (TFR, plot (a)) and the rates of correct predictions (RCP, plot (b)). The straight lines show the linear fit for our procedure (full line) and the MRC procedure (dashed lines). The horizontal axis indicates the number of proteins for which a prediction has been made. All rates in the vertical axis are computed with respect to the total number of annotated proteins.
The RCP criteria decreases with decreasing threshold d: the less strict we are, the more predictions we make, but the lower the quality of the predictions is. It varies between 41% and 70% for the MRC procedure, whereas it is constantly above 50% for the hybrid procedure (Fig. 3b). Interestingly, when plotted against the number of predictions, the points seem to lie on two strait and parallel lines. Indeed, linear regressions (straight lines in Fig. 3) fit well with both sets of data, and confirm that the RCP criteria is constantly above for the hybrid procedure with respect to the MRC procedure. The improvement is about 3%. If we chose to be very conservative, our method allows to achieve a rate of correct predictions of 75% for a small number of proteins.
As for the rate of true functions recovered (TFR), the difference between both procedures is even more striking (see Fig. 3a). It augments when the threshold d becomes less stringent and thus when the number of predictions increases. However, as seen previously, the price to pay is a poor reliability of the prediction. Clearly, the hybrid procedure yields better results than the simple majority rule. We apply again a linear regression to both sets of data, which confirms that the hybrid procedure achieves a TFR rate which is 4 to 7% better than the MRC procedure for the same number of predictions. A very conservative approach yields TFR rates of 45% for the hybrid and 41% for the MRC procedure, while a less severe approach yields rates well over 50% for the first procedure against 45% for the second.
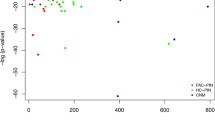
In comparison, the performances of the MRN method are limited, as can be seen immediately from the ROC curve in Fig. 4, in which the TFR is plotted against the RCP. Here, we assigned to a protein the n most represented functions among its direct interaction partners, with n = 1... 5. However, this method makes a prediction for almost all the proteins, since having one annotated interaction partner is enough for a protein to get a function. The poor performances of this approach emphasizes the need for more refined approaches which takes into account the specific neighborhood of each protein.
Comparison between the hybrid method (blue squares), the MRC method (red diamonds) and the MRN [4] (green triangle). The rate of true functions recovered is plotted agains the rate of correct predictions. For the hybrid method and the MRC method, the points correspond to thresholds d from 30% to 70% in steps of 5%, whereas for the MRN method the points correspond to predictions made with the n most frequent functions represented among direct interaction partners, with n = 1...5.
Finally, we have tried to confront the quality of the predictions made by our method, with respect to the GOM. In order to do so, out of the 37 uncharacterized proteins we made a prediction for, we took the 12 which had received an annotation in the meantime based on experimental evidence, and compared our predictions as well as the GOM predictions to these newly acquired annotations. Results of this analysis are presented in Table 2. Overall, whereas 8/12 (67%) of our predictions are equal or strongly similar to the current SGD annotation, only 2/9 GOM predictions (22%) do match the SGD annotation. Moreover, in 3 out of 7 cases where the GOM prediction of was different (NIS1, SLX4, YLR238W), this prediction was rated as a high confidence prediction by the authors (100/100, see [8] supplementary material). In conclusion, the comparison with alternative methods proposed so far shows that our approach performs better and makes more reliable predictions.
Discussion and conclusion
We have proposed a new method to analyze the protein-protein interaction network grounded on the combination of a clustering algorithm of the vertices and a refined method allowing to assign a function to proteins of yet unknown function. This method builds classes of proteins which appear to be involved in the same or related biological process(es). Furthermore, the method proposes a number of highly biologically relevant classes that PRODISTIN was not able to pinpoint. The results of our method are very encouraging, since the improvement we propose is a very simple one and yields sizeable effects for a significant number of uncharacterized proteins. Comparison with alternative approaches (MRN [4] or GOM [8]) shows that the performance of our algorithm is better in terms of sensibility and/or specificity, and that the predictions seem more reliable. It is especially interesting that it performs better for the rate of recovered functions, since this is probably the most relevant indicator. Indeed, the rate of correct predictions for example is very sensitive to incomplete annotations (false positive might turn out to be true positives). We have no doubt that there is still room for improvement. For example, the annotation procedure should be optimized to become even more context sensitive, as some classes have very coherent protein functions, while the annotations inside others seem more broadly distributed. This does not mean that the procedure is inadequate, but may reflect the incompleteness of the biological knowledge. Another improvement might come from using the extended classes of the clustering algorithm instead of the partitions, as the density of interactions inside the extended classes is higher than in the partitions. Thus, the quality of the predictions is likely to be further increased.
Author's contributions
CB provided the manually curated datasets and carried out the biological expertise of the protein clusters formed, CH developed the annotation procedure, applied it to the protein clusters, and did the comparison with other methods. AG developed the clustering algorithm, carried out the validation procedure and supervised the whole project. All authors read and approved the final manuscript.
References
Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, Qureshi-Emili A, Li Y, Godwin B, Conover D, Kalbfleisch T, Vijayadamodar G, Yang M, Johnston M, Fields S, Rothberg JM: A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae. Nature 2000, 403(6770):623–7. [Eng Journal Article]. 10.1038/35001009
Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y: A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc Natl Acad Sci U S A 2001, 98(8):4569–74. [Eng Journal Article]. 10.1073/pnas.061034498
Giot L, Bader JS, Brouwer C, Chaudhuri A, Kuang B, Li Y, Hao YL, Ooi CE, Godwin B, Vitols E, Vijayadamodar G, Pochart P, Machineni H, Welsh M, Kong Y, Zerhusen B, Malcolm R, Varrone Z, Collis A, Minto M, Burgess S, McDaniel L, Stimpson E, Spriggs F, Williams J, Neurath K, Ioime N, Agee M, Voss E, Furtak K, Renzulli R, Aanensen N, Carrolla S, Bickelhaupt E, Lazovatsky Y, DaSilva A, Zhong J, Stanyon CA, Finley JRL, White KP, Braverman M, Jarvie T, Gold S, Leach M, Knight J, Shimkets RA, McKenna MP, Chant J, Rothberg JM: A protein interaction map of Drosophila melanogaster. Science 2003, 302(5651):1727–36. [Journal Article]. 10.1126/science.1090289
Schwikowski B, Uetz P, Fields S: A network of protein-protein interactions in yeast. Nat Biotechnol 2000, 18(12):1257–61. [Eng Journal Article]. 10.1038/82360
Brun C, Wojcik J, Guénoche A, Jacq B: Bioinformatic study of interaction networks: PRODISTIN, a new method for a functionnal classification of proteins. In Journées Ouvertes Biologie Informatique Mathématiques (JOBIM'2002) (Edited by: Nicolas J, Thermes C). Saint Malo, France 2002, 171–182.
Brun C, Chevenet F, Martin D, Wojcik J, Guénoche A, Jacq B: Functional classification of proteins for the prediction of cellular function from a protein-protein interaction network. Genome Biol 2003, 5: R6. 10.1186/gb-2003-5-1-r6
Samanta MP, Liang S: Predicting protein functions from redundancies in large-scale protein interaction networks. Proc Natl Acad Sci U S A 2003, 100(22):12579–83. [0027–8424 Journal Article]. 10.1073/pnas.2132527100
Vazquez A, Flammini A, Maritan A, Vespignani A: Global protein function prediction from protein-protein interaction networks. Nat Biotechnol 2003, 21(6):697–700. [Evaluation Studies Journal Article]. 10.1038/nbt825
Bader GD, Hogue CW: An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinformatics 2003, 4: 2. [1471–2105 Evaluation Studies Journal Article]. 10.1186/1471-2105-4-2
Rougemont J, Hingamp P: DNA microarray data and contextual analysis of correlation graphs. BMC Bioinformatics 2003, 4: 15. [1471–2105 Journal Article Validation Studies]. 10.1186/1471-2105-4-15
Rives AW, Galitski T: Modular organization of cellular networks. Proc Natl Acad Sci U S A 2003, 4: 1128–1133. 10.1073/pnas.0237338100
Timblin BK, Tatchell K, Bergman LW: Deletion of the gene encoding the cyclin-dependent protein kinase Pho85 alters glycogen metabolism in Saccharomyces cerevisiae. Genetics 1996, 143: 57–66. [0016–6731 Journal Article].
Tong AH, Lesage G, Bader GD, Ding H, Xu H, Xin X, Young J, Berriz GF, Brost RL, Chang M, Chen Y, Cheng X, Chua G, Friesen H, Goldberg DS, Haynes J, Humphries C, He G, Hussein S, Ke L, Krogan N, Li Z, Levinson JN, Lu H, Menard P, Munyana C, Parsons AB, Ryan O, Tonikian R, Roberts T, Sdicu AM, Shapiro J, Sheikh B, Suter B, Wong SL, Zhang LV, Zhu H, Burd CG, Munro S, Sander C, Rine J, Greenblatt J, Peter M, Bretscher A, Bell G, Roth FP, Brown GW, Andrews B, Bussey H, Boone C: Global mapping of the yeast genetic interaction network. Science 2004, 303(5659):808–13. [1095–9203 Journal Article]. 10.1126/science.1091317
Acknowledgements
This work is supported by the ACI IMP-Bio project EIDIPP (2003) and an Action Inter-EPST 2002–2004 grant to AG. We thank Bernard Jacq for careful reading of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
12859_2004_211_MOESM1_ESM.pdf
Additional File 1: list of the 126 classes obtained with the clustering-algorithm described in the text (d = 50%), along with their respective annotations when available. (PDF 38 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Brun, C., Herrmann, C. & Guénoche, A. Clustering proteins from interaction networks for the prediction of cellular functions. BMC Bioinformatics 5, 95 (2004). https://doi.org/10.1186/1471-2105-5-95
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-5-95