Abstract
Background
Gene expression analysis has emerged as a major biological research area, with real-time quantitative reverse transcription PCR (RT-QPCR) being one of the most accurate and widely used techniques for expression profiling of selected genes. In order to obtain results that are comparable across assays, a stable normalization strategy is required. In general, the normalization of PCR measurements between different samples uses one to several control genes (e.g. housekeeping genes), from which a baseline reference level is constructed. Thus, the choice of the control genes is of utmost importance, yet there is not a generally accepted standard technique for screening a large number of candidates and identifying the best ones.
Results
We propose a novel approach for scoring and ranking candidate genes for their suitability as control genes. Our approach relies on publicly available microarray data and allows the combination of multiple data sets originating from different platforms and/or representing different pathologies. The use of microarray data allows the screening of tens of thousands of genes, producing very comprehensive lists of candidates. We also provide two lists of candidate control genes: one which is breast cancer-specific and one with more general applicability. Two genes from the breast cancer list which had not been previously used as control genes are identified and validated by RT-QPCR. Open source R functions are available at http://www.isrec.isb-sib.ch/~vpopovic/research/
Conclusion
We proposed a new method for identifying candidate control genes for RT-QPCR which was able to rank thousands of genes according to some predefined suitability criteria and we applied it to the case of breast cancer. We also empirically showed that translating the results from microarray to PCR platform was achievable.
Similar content being viewed by others
Background
Real-time quantitative reverse transcription PCR (RT-QPCR) has become a method of choice for gene expression profiling in a large number of applications. However, obtaining reliable measurements still depends on the choice of control genes on which the baseline level is constructed. Selecting the control genes remains a critical point in the normalization process. Often, a short list of candidates is produced based on non-systematic and/or often poorly defined biological considerations.
In early studies, normalization was usually based on a single control gene. More recently, the trend is to use several control genes whose average expression level (on a log-scale) is used as baseline [1, 2]. Suitable control genes are selected from a short list of 10–15 genes by ranking them according to a criterion that essentially selects those genes having low variation across samples. We describe brie y a few such methods below.
[2] introduces a stability coefficient which is used along with the coefficient of variation for ranking the genes from a predefined list of candidates. Gene stability is defined in terms of average standard deviation of the log-ratios of pairs of candidate genes. Genes are ranked by iteratively removing those most unstable. This approach has the drawback that repeated comparison of pairs of genes is required, which is feasible only when the number of candidates is small. In addition, the method implicitly assumes that there are no co-regulated genes. A model-based approach proposed by [1] aims at estimating the overall variation as well as the between sample variation of each candidate gene. However, with this approach it is cumbersome to integrate different platforms. In an application to plant pathogen profiling, [3] investigates a list of 18 pre-selected candidate housekeeping genes, using the method proposed in [2] and RT-QPCR for measuring the gene expressions. [4] proposes a PCA-based statistical analysis to identify the most suitable control genes among 13 candidates which were selected such that they had independent functions in cellular maintenance.
[5] introduces a strategy which combines the coefficient of variation, maximum fold change and mean expression value in a ranking criterion that is applied to a large number of samples representing a wide variety of tissues. All these samples were hybridized on either Affymetrix HG-U133A or HG-U133 Plus 2.0 arrays and quantile-normalized together prior to ranking. Only probesets common to both arrays were used, with probesets targeting the same gene averaged into a single value.
There are some important differences between the methods described above and our approach (described below). Firstly, in contrast with all the studies based on PCR, we do not require a short list of candidate genes to be produced before assessing their suitability as control genes. Instead, we screen all the genes represented on the microarray chips, giving us the opportunity to assess genes that have not been reported previously. Moreover, we take a meta-analytical approach to the problem, first creating an independent ranking within each data set then aggregating these rankings into a single list. This approach has the advantage of being platform- and normalization-independent. In addition, the approach is not limited to using only genes common between different data sets. Also, by not using the coefficient of variation, we can treat uniformly both single and two-colors arrays. Thus, we are able to exploit data obtained from different platforms without requiring them to be normalized together. Furthermore, the meta-analytical approach allows us to integrate gene lists produced using our ranking system with other ranked gene lists from the literature and we do not require all data to be normalized together. Another key difference is that we introduce a new stability coefficient that combines the mean expression and the standard deviation in a ranking criterion that corresponds to our requirements for candidate control genes for RT-QPCR. In general, these requirements are:
-
low variability across different specimens (e.g., subtypes of tumors or normal tissues);
-
high and moderate level of expression, such that control genes with expression levels across a larger range may be selected;
-
consistency across experiments and platforms.
A key question is whether it is possible to select genes from microarray studies that perform as control genes on PCR platform, given that the two technologies are different. We hypothesize that translating the list of candidate genes from microarray to PCR platform is feasible and we provide empirical evidence in this sense.
Results
Data sets and pre-processing steps
We have collected ten publicly available data sets [6–15], listed in Table 1, from which we derived the quantities of interest: the mean and standard deviations of the log-intensities (on Affymetrix platforms) or of the log-ratios (on Agilent platforms).
We note here that the original EXPO data set contains a number of different pathologies, but we restrict analysis here to eight different types of cancer (breast, colon, endometrium, kidney, lung, ovary, prostate and uterus) for which a sufficient number of samples existed. EXPO breast cancer samples (n = 328) were used to produce both the breast cancer and general cancer lists of candidate genes.
The Affymetrix data are available as MAS5.0 normalized values. The Agilent data contains log-ratios (base 10) and mean-centered log-intensities. The standard deviations of log-intensities (Affymetrix) and log-ratios (Agilent) were used as measures of variability. The means of log-intensities (both Affymetrix and Agilent) were used as measures of average expression level.
When multiple probesets of the same gene are present, only the most variable one is used. We consider all genes from each platform, the aggregation methods used being able to cope with 'missing' genes (those not represented on the array). Considering only those genes common to all platforms is an unnecessary limiting constraint, as increasing the number of data sets and the heterogeneity of the collection leads to a successively smaller intersection of genes.
Before any further usage of the data, we reduce the variability across platforms by scaling with a factor given by a first order LOESS fit of the data. The effect of this transformation can be seen in Figure 1, where the black line represents the fitted curve. This simple approach seems effective, except for genes with low expression. However, as we are interested in genes with higher mean expression, this deficiency is not problematic.
Ranking the genes
Let us consider that we have M microarray data sets, each containing expression values of a set of genes G k , k = 1,...,M, and let G = ∪ k G k = {1,...,N} be the set of all genes represented at least once in any of these data sets.
Gene scores
We aim to design a scoring function which ranks the genes such that higher scores correspond to genes that are more suitable to be used as control genes. As mentioned above, the score has to combine each gene's mean expression and standard deviation into a single value such that higher expression levels and lower variances (standard deviations) are favored. Moreover, the score must be independent of the technology used to measure expression levels and the method for normalization.
These requirements lead us to propose a new stability score for the gene expression levels. This score for gene i in data set k, denoted s ik , is defined as
where and are the estimated mean log-intensity and the standard deviation of the gene i in data set k. The α coefficient allows the user to control the trade-off between the mean expression and the standard deviation in gene scoring. Results reported here were obtained with α = 0.25. The β k parameter allows one to define the level of mean expression below which the genes are not considered for ranking, i.e. the score for these genes is -∞. We have set β k to be the 25th percentile of the mean expression, for each data set k. Genes having a higher score are considered more suitable as control genes. As we see from Eq. 1, high variation in gene expression leads to a lower score when mean expression levels are equal. This is one reason we select the most highly variable probeset from the probesets representing the same gene, in order to encompass the worst-case scenario. Note also that there is no need to normalize the scores to make them comparable across data sets, because they are used solely for ranking the genes within the same data set. Finally, having computed the scores for all the genes within a data set, we order the genes from high to low values of the scores, with ties resolved by ordering by the mean expression (from high to low). From this perspective, the scores can be seen as defining classes of equivalence among genes: all the genes in the same class (having the same score) are equally useful as normalization genes. By using the second ordering criterion, we can select control genes with a desired expression level (examples of classes of equivalence are the equal score levels in Figure 2).
Scatter plots of standard deviation versus mean log-intensity for BWH, NKI and EXPO-breast data sets, respectively. The shading codes the gene stability scores, with darker colors indicating higher scores. These three data sets are from different microarray platforms. The light gray points indicate the discarded genes (those with mean expression level below the β value – see Eq. 1). The curves correspond to equal score levels and are one score unit apart.
Figure 2 displays the influence of the mean expression level and the standard deviation on the gene score. All genes located on the curves have the same score value (they belong to the same equivalence class). Two consecutive curves are separated by one score unit.
Using this stability score, we ranked the genes from each data set, obtaining the lists that will be later combined. An excerpt from the ten lists for the breast cancer data sets is shown in Table 2 (first ten columns).
Combining results from different data sets
Once genes are ranked according to their scores in each data set (lower ranks correspond to higher scores), the natural next step is to combine these rankings into a global ranked list. We combine the ranks of the genes rather than their scores to avoid normalizing the scores across different data sets, thereby achieving platform-independence. To this end we use the rank product score [16], which is a fast and efficient method for combining ranked lists. It computes, for each gene i ∈ G, a new score
where rank k (i) is the rank of s ik , the score for gene i in data set k (topmost gene has the rank 1), and n i is the number of data sets in which the gene i appears. The final list is obtained by sorting the genes in increasing order of R i . The top 20 genes from the aggregated breast cancer list are given in the 'Meta' (last) column of Table 2.
Validation of the aggregated lists
There is no absolute criterion by which one can judge the quality of the resulting lists. Rather, the aggregated list could be used to select from the top genes (100, for example) those genes that also satisfy further conditions of the specific application.
We can, however, have a subjective impression of the validity of the aggregated list by visualizing the resulting top genes in data sets not used for producing the list. We obtained a list of the top 100 genes by applying the method described above on eight of the ten data sets, leaving NKI and UPP aside as validation sets. The top 100 genes in both validation sets (different microarray platforms) are plotted in Figure 3. As a comparison, we also include the five control genes used in [17] (represented as triangles in the figure). It is seen that the genes are generally concentrated in the lower right part of the plot, corresponding to high mean expression levels and low variance. There is a notable difference between the quality of the results (given by the concentration of the control genes in the lower right corner) on the two platforms, due to the fact that most of the data sets used for gene selection are from Affymetrix platforms. While the top 100 lists contain genes with high stability scores on the Affymetrix platforms (the UPP data set), on the custom Agilent platform (NKI) there are a number of genes that are missed. Nevertheless, those selected still function well as control genes.
Scatter plots of standard deviation versus mean log-intensity for two validation data sets (from left to right: NKI and UPP). The top 100 breast cancer control genes resulting from aggregating eight data sets are plotted as circles. Triangles correspond to the five control genes used in [17] (NKI does not contain the ACTB gene).
Control genes lists
We have analyzed ten different data sets which have samples hybridized on different versions of Agilent and Affymetrix platforms. Using our proposed method, we compiled two different lists of candidate control genes: one specific to breast cancer [see Additional file 1] and one resulting from the analysis of eight different types of cancer, thus applicable to cancers in general [see Additional file 2]. From the breast cancer list we selected two new control genes which were validated in an RT-QPCR assay that also included five previously used control genes (ACTB, TFRC, GUSB, RPLP0 and GAPDH – see [17]) and breast cancer-related genes (e.g. ESR1, ERBB2, AURKA, etc.). The RT-QPCR results confirm the findings from the microarray analysis and show that more stably expressed control genes can be selected by applying the criteria mentioned above. Also, they provide empirical evidence supporting the working hypothesis that PCR control genes can be selected from microarray data.
The list of the top 50 control genes obtained from the ten breast cancer data sets is given in Table 3. More comprehensive lists, including one containing the top 2000 candidate breast cancer genes and a similar list compiled from eight different types of cancer, are available [see Additional file 1 and Additional file 2]. In the case of breast cancer control genes, it is interesting to note that some of the "classical" genes (e.g. ACTB, GAPDH, TFRC) are not among the top 50.
Evaluation of control genes by RT-QPCR
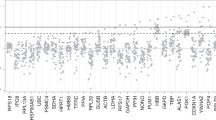
Motivated by the consistency of the selection process for suitable control genes among different microarray platforms, we performed a small scale RT-QPCR experiment to test the performance of two new control genes along with a number of more commonly used control genes. In this experiment, RNA was isolated from 25 cryo-preserved breast cancer samples and the expression of 47 genes was measured by RT-QPCR [18]. Test genes were selected according to their relatedness to proliferation or estrogen receptor functions. Some of the test genes had been previously identified and used for characterizing primary breast cancers [17]. Two genes, RPS11 and UBB, ranked 9 and 31 in Table 3 respectively, were compared to five additional control genes and to a number of test genes previously measured by [17]. Mean raw expression values of all candidate control and test genes were plotted against standard deviations of each gene (Figure 4). The raw Ct (cycle threshold) value is the number of PCR cycles required for the fluorescence signal to cross the background threshold, so that low Ct values correspond to high expression levels. RPS11 and UBB are clearly among the most stably expressed genes, as their standard deviations are both quite low. Other genes frequently used as control genes are also shown. For comparison, mean expression and standard deviation of several test genes are also indicated. The expression of most test genes is much more variable than UBB and RPS11.
RT-QPCR experiment. Standard deviation as a function of the mean expression level (expressed as raw Ct values) of 47 genes in a RT-QPCR experiment. Higher expression levels correspond to smaller raw Ct values. Control genes are represented by triangles, test genes by circles. The new control genes RPS11 and UBB are in the lower left corner.
The two new control genes, together with RPLP0, offer the best trade-off between mean expression level and variability, while others like ACTB or TFRC are less stably expressed and therefore seem less suitable for use as normalization genes.
Discussion
We propose a new approach which leverages publicly available microarray data to produce lists of candidate control genes for RT-QPCR. Our method is independent of the microarray platform or normalization methodology, and is able to cope with gene lists that overlap only partially. After screening thousands of genes (generally more than 10,000 genes in each data set), we have produced two separate lists of candidate genes: one specific to breast cancer and one generally applicable to different types of cancer. We do not consider these lists as generally applicable, as the data used do not allow such generalization. Different pathologies may have a different impact on the control genes and some of the control genes we selected may become ineffective in the case of a disease which affects their particular functions. On the other hand, more diverse data should be used if the goal is finding global control genes. The list of the top 50 breast cancer control genes (Table 3) is dominated by ribosomal proteins. This finding is consistent with the fact that ribosomes are a major component of basic physiologic processes in all the cells and not a primary target of changing conditions. Other genes present among the first 50 genes code for protein turnover (ubiquitin), tubulin-related proteins or actins, structures which are required in all living cells.
Our results are supported by recent findings of de Jonge et al. [5], who used a different ranking method. In addition, the lists of control gene candidates for breast cancer and for diverse types of cancer are similar [see Additional file 1 and Additional file 2], as a large number of the top ranked genes belong to the same functional category (ribosomal genes, protein turnover).
Another important finding is that some of the commonly used control genes in breast cancer (ACTB and TFRC) appear to be less stable than previously assumed. This has an impact on the normalization strategy of the QPCR measurements: indeed, in our more recent experiments we have chosen to use the mean of RPLP0, RPS11 and UBB (on the log2 scale) for normalizing the expression of test genes.
Finally, we would like to emphasize that these two lists should not be taken in an absolute sense: a gene in top 10 is not necessarily a better choice than a gene in the top 20 to 30. But we do consider it to be definitely a better candidate than a gene not in top 100. Nor do we consider the resulting ranking as providing a solution to the problem of finding normalization genes in all contexts. Rather, the lists produced through this process are meant to guide the choice of control genes while also taking into consideration the specific requirements of any individual analysis. Depending on the planned application, other parameters must be considered. For example, short amplicons or intron-spanning primers must be used when the starting RNA is considerably degraded or when residual DNA contaminations might affect QPCR. The final choice of control genes should be made not by blind adherence to the ranked list, but be imposed by the intended application.
Conclusion
Starting from clearly defined criteria, we have designed a novel method for ranking the candidate genes for their suitability as control genes in RT-QPCR experiments. The genes from a data set were ranked according to their stability score, which represented a trade-off between gene's average expression level and its variance. Finally, the rankings from several data sets were combined into a list of candidate genes, with higher ranked genes being considered to be more suitable as control genes. The proposed approach had the advantage of being platform- and normalization- independent and of not being restricted to only the list of common genes across all data sets.
By applying the proposed method to two particular collections of data sets we were able to produce two lists of candidate genes from which control genes for either breast cancer or more diverse cancer could be easily selected. Two new control genes for breast cancer – UBB and RPS11 – have been identified and validated by RT-QPCR.
Our results support the hypothesis that selecting control genes for QPCR from microarray data is feasible.
References
Andersen CL, Jensen JL, Ørntoft TF: Normalization of real-time quantitative reverse transcription-PCR data: a model-based variance estimation approach to identify genes suited for normalization, applied to bladder and colon cancer data sets. Cancer Research 2004, 64(15):5245–5250. 10.1158/0008-5472.CAN-04-0496
Vandesompele J, Preter KD, Pattyn F, Poppe B, Roy NV, Paepe AD, Speleman F: Accurate normalization of real-time quantitative RT-PCR data by geometric averaging of multiple internal control genes. Genome Biology 2002, 3(7):RESEARCH0034. 10.1186/gb-2002-3-7-research0034
Yan HZ, Liou RF: Selection of internal control genes for real-time quantitative RT-PCR assays in the oomycete plant pathogen Phytophthora parasitica. Fungal Genet Biol 2006, 43(6):430–438. 10.1016/j.fgb.2006.01.010
de Kok JB, Roelofs RW, Giesendorf BA, Pennings JL, Waas ET, Feuth T, Swinkels DW, Span PN: Normalization of gene expression measurements in tumor tissues: comparison of 13 endogenous control genes. Laboratory Investigations 2005, 85: 154–159.
de Jonge HJM, Fehrmann RSN, de Bont ESJM, Hofstra RMW, Gerbens F, Kamps WA, de Vries EGE, Zee AGJ, te Meerman GJ, ter Elst A: Evidence based selection of housekeeping genes. PLoS ONE 2007, 2(9):e898. 10.1371/journal.pone.0000898
Richardson AL, Wang ZC, Nicolo AD, Lu X, Brown M, Miron A, Liao X, Iglehart JD, Livingston DM, Ganesan S: X chromosomal abnormalities in basal-like human breast cancer. Cancer Cell 2006, 9(2):121–132. 10.1016/j.ccr.2006.01.013
Wang Y, Klijn JGM, Zhang Y, Sieuwerts AM, Look MP, Yang F, Talantov D, Timmermans M, van Gelder MEM, Yu J, Jatkoe T, Berns EMJJ, Atkins D, Foekens JA: Gene-expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer. Lancet 2005, 365(9460):671–679.
IGC: Expression Project for Oncology.2008. [http://www.intgen.org/expo.cfm]
Sotiriou C, Wirapati P, Loi S, Harris A, Fox S, Smeds J, Nordgren H, Farmer P, Praz V, Haibe-Kains B, Desmedt C, Larsimont D, Cardoso F, Peterse H, Nuyten D, Buyse M, de Vijver MJV, Bergh J, Piccart M, Delorenzi M: Gene expression profiling in breast cancer: understanding the molecular basis of histologic grade to improve prognosis. J Natl Cancer Inst 2006, 98(4):262–272.
Ma XJ, Wang Z, Ryan PD, Isakoff SJ, Barmettler A, Fuller A, Muir B, Mohapatra G, Salunga R, Tuggle JT, Tran Y, Tran D, Tassin A, Amon P, Wang W, Wang W, Enright E, Stecker K, Estepa-Sabal E, Smith B, Younger J, Balis U, Michaelson J, Bhan A, Habin K, Baer TM, Brugge J, Haber DA, Erlander MG, Sgroi DC: A two-gene expression ratio predicts clinical outcome in breast cancer patients treated with tamoxifen. Cancer Cell 2004, 5(6):607–616. 10.1016/j.ccr.2004.05.015
Vijver MJ, He YD, van't Veer LJ, Dai H, Hart AAM, Voskuil DW, Schreiber GJ, Peterse JL, Roberts C, Marton MJ, Parrish M, Atsma D, Witteveen A, Glas A, Delahaye L, Velde T, Bartelink H, Rodenhuis S, Rutgers ET, Friend SH, Bernards R: A gene-expression signature as a predictor of survival in breast cancer. N Engl J Med 2002, 347(25):1999–2009. 10.1056/NEJMoa021967
Pawitan Y, Bjöhle J, Amler L, Borg AL, Egyhazi S, Hall P, Han X, Holmberg L, Huang F, Klaar S, Liu ET, Miller L, Nordgren H, Ploner A, Sandelin K, Shaw PM, Smeds J, Skoog L, Wedrén S, Bergh J: Gene expression profiling spares early breast cancer patients from adjuvant therapy: derived and validated in two population-based cohorts. Breast Cancer Res 2005, 7(6):R953-R964. 10.1186/bcr1325
Farmer P, Bonnefoi H, Becette V, Tubiana-Hulin M, Fumoleau P, Larsimont D, Macgrogan G, Bergh J, Cameron D, Goldstein D, Duss S, Nicoulaz AL, Brisken C, Fiche M, Delorenzi M, Iggo R: Identification of molecular apocrine breast tumours by microarray analysis. Oncogene 2005, 24(29):4660–4671. 10.1038/sj.onc.1208561
Hu Z, Fan C, Oh DS, Marron JS, He X, Qaqish BF, Livasy C, Carey LA, Reynolds E, Dressler L, Nobel A, Parker J, Ewend MG, Sawyer LR, Wu J, Liu Y, Nanda R, Tretiakova M, Orrico AR, Dreher D, Palazzo JP, Perreard L, Nelson E, Mone M, Hansen H, Mullins M, Quackenbush JF, Ellis MJ, Olopade OI, Bernard PS, Perou CM: The molecular portraits of breast tumors are conserved across microarray platforms. BMC Genomics 2006, 7: 96. 10.1186/1471-2164-7-96
Miller LD, Smeds J, George J, Vega VB, Vergara L, Ploner A, Pawitan Y, Hall P, Klaar S, Liu ET, Bergh J: An expression signature for p53 status in human breast cancer predicts mutation status, transcriptional effects, and patient survival. Proc Natl Acad Sci USA 2005, 102(38):13550–13555. 10.1073/pnas.0506230102
Breitling R, Armengaud P, Amtmann A, Herzyk P: Rank products: a simple, yet powerful, new method to detect differentially regulated genes in replicated microarray experiments. FEBS Lett 2004, 573(1–3):83–92. 10.1016/j.febslet.2004.07.055
Paik S, Shak S, Tang G, Kim C, Baker J, Cronin M, Baehner FL, Walker MG, Watson D, Park T, Hiller W, Fisher ER, Wickerham DL, Bryant J, Wolmark N: A multigene assay to predict recurrence of tamoxifen-treated, node-negative breast cancer. N Engl J Med 2004, 351(27):2817–2826. 10.1056/NEJMoa041588
Oberli A, Popovici V, Delorenzi M, Baltzer A, Antonov J, Matthey S, Aebi S, Altermatt HJ, Jaggi R: Expression profiling with RNA from formalin-fixed, paraffin-embedded material. BMC Med Genomics 2008, 1: 9. 10.1186/1755-8794-1-9
Acknowledgements
This work has been funded by the Swiss National Science Foundation through the National Centre for Competence in Research (Molecular Oncology (MD, VP and PW)) and the National Centre for Competence in Research (Plant Survival (DRG)), and by the Swiss Cancer League (Project OCS 01704-04-2005 (RJ and MD)).
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
VP conducted the analysis, devised algorithms and wrote the computer programs. PW collected the datasets and remapped the probes. PW, DRG and MD designed the study and statistical analyses. JA and RJ initiated the biological problems and conducted the RT-PCR validation. All authors have read and approved the final manuscript.
Electronic supplementary material
12859_2008_2772_MOESM1_ESM.xls
Additional file 1: Top 2000 breast cancer candidate control genes. Excel file containing top 2000 genes as resulted from combining the ten breast cancer data sets. (XLS 474 KB)
12859_2008_2772_MOESM2_ESM.xls
Additional file 2: Top 2000 diverse cancer candidate control genes. Excel file containing top 2000 genes as resulted from combining the eight different types of cancer from the EXPO data set. (XLS 391 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Popovici, V., Goldstein, D.R., Antonov, J. et al. Selecting control genes for RT-QPCR using public microarray data. BMC Bioinformatics 10, 42 (2009). https://doi.org/10.1186/1471-2105-10-42
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-10-42