Abstract
Background
Two key findings from genomic selection experiments are 1) the reference population used must be very large to subsequently predict accurate genomic estimated breeding values (GEBV), and 2) prediction equations derived in one breed do not predict accurate GEBV when applied to other breeds. Both findings are a problem for breeds where the number of individuals in the reference population is limited. A multi-breed reference population is a potential solution, and here we investigate the accuracies of GEBV in Holstein dairy cattle and Jersey dairy cattle when the reference population is single breed or multi-breed. The accuracies were obtained both as a function of elements of the inverse coefficient matrix and from the realised accuracies of GEBV.
Methods
Best linear unbiased prediction with a multi-breed genomic relationship matrix (GBLUP) and two Bayesian methods (BAYESA and BAYES_SSVS) which estimate individual SNP effects were used to predict GEBV for 400 and 77 young Holstein and Jersey bulls respectively, from a reference population of 781 and 287 Holstein and Jersey bulls, respectively. Genotypes of 39,048 SNP markers were used. Phenotypes in the reference population were de-regressed breeding values for production traits. For the GBLUP method, expected accuracies calculated from the diagonal of the inverse of coefficient matrix were compared to realised accuracies.
Results
When GBLUP was used, expected accuracies from a function of elements of the inverse coefficient matrix agreed reasonably well with realised accuracies calculated from the correlation between GEBV and EBV in single breed populations, but not in multi-breed populations. When the Bayesian methods were used, realised accuracies of GEBV were up to 13% higher when the multi-breed reference population was used than when a pure breed reference was used. However no consistent increase in accuracy across traits was obtained.
Conclusion
Predicting genomic breeding values using a genomic relationship matrix is an attractive approach to implement genomic selection as expected accuracies of GEBV can be readily derived. However in multi-breed populations, Bayesian approaches give higher accuracies for some traits. Finally, multi-breed reference populations will be a valuable resource to fine map QTL.
Similar content being viewed by others
Background
Genomic selection refers to selection decisions based on genomic estimated breeding values (GEBV) [1]. To calculate GEBV, first a prediction equation based on a large number of DNA markers, such as SNP (Single Nucleotide Polymorphisms) markers, is derived. The effects of these markers are estimated in a reference population in which animals are both phenotyped and genotyped. In subsequent generations, animals can be genotyped for the markers and the effects of the genotypes summed across the whole genome to predict the GEBV. Recently, the accuracy of GEBV predicted in this way has been evaluated in experiments involving dairy cattle populations in the United States, New Zealand, Australia, and the Netherlands [2–4]. These experiments used reference populations of between 650 and 4,500 progeny-tested Holstein-Friesian bulls, genotyped for approximately 50,000 genome-wide markers. Accuracies of GEBV for young bulls whose phenotypes were not used in the reference population were between 0.4 and 0.82 across a range of traits.
A key finding from experiments conducted to date is that the reference population must be very large to subsequently predict accurate GEBV. For example in one experiment the gain in coefficient of determination of GEBV for bulls in a validation data set on their daughter deviations for net merit (R2) was investigated as the number of bulls in the reference set increased from 1151 bulls to 3576 bulls [2]. There was a linear increase in R2 with the number of bulls in the reference set over this range, with every 100 bulls adding 0.008 to R2 [2]. Given this result, assembling reference populations large enough to achieve high accuracies of GEBV will present a major challenge for breeds which have limited numbers of genotyped and phenotyped animals.
One potential solution would be to use the prediction equation from a breed with a large reference population to predict GEBV in other breeds. However this strategy does not hold much promise: it has been reported that SNP estimates calculated from a Holstein-Friesian reference population did not produce accurate GEBV in Jersey bulls, and vice versa [4]. Correlations ranged from -0.1 to 0.3 when the SNP effects from one breed were used to calculate GEBV in another breed [4]. Genomic selection relies on the assumption that phases of linkage disequilibrium (LD) between markers and quantitative trait loci (QTL) are the same in selection candidates and the reference population. Thus one explanation for the across-breed results is that the SNP are in LD with the QTL within a breed, but not across breeds. Another experiment analysed the extent of LD within and between several beef and dairy breeds, and concluded that for breeds as divergent as Holstein and Jersey, markers would have to be 10 kb apart or less (much denser than the approximately 65 kb density used in the above experiments) for marker-QTL phase to persist across breeds [5]. Another complication is that the effect of QTL alleles may not be the same in different breeds and populations, or that the QTL may not be segregating across breeds.
A different solution would be to use a multi-breed reference population, perhaps with limited numbers of secondary breeds, so that potentially all the genetic variants segregating within and across breeds are captured. This strategy has been evaluated using simulated data [6]. It was demonstrated that using a multi-breed reference population with relatively few individuals of the second breed could improve the accuracy of GEBV for that second breed, provided markers were sufficiently dense and the breeds were not too diverged.
In this work, we have investigated the accuracy of GEBV for dairy production traits in Holstein dairy cattle and Jersey dairy cattle when the reference population consists of Holstein bulls only, Jersey bulls only, or bulls of both breeds, with all bulls genotyped for approximately 50,000 markers. Accuracies were evaluated for two types of methods. The first set of methods estimated individual SNP effects in the reference population, and then predicted GEBV for selection candidates by summing the SNP effects across the marker genotype they carried. The second set of methods predicted breeding values by replacing the average relationship matrix with the genomic relationship matrix in best linear unbiased prediction (BLUP) equations
Another significant challenge in the implementation of genomic selection is to derive an expected accuracy of GEBV, as is current practise for EBV in national genetic evaluations [7]. In this study we have also investigated the agreement of expected accuracies obtained as a function of elements of the inverse coefficient matrix when a genomic relationship matrix is used, with accuracies of GEBV obtained by correlating GEBV and breeding values for bulls with a large number of daughters in both single breed and multi-breed populations.
Methods
Samples and SNP
One thousand and two hundred Holstein bulls and 400 Jersey bulls were genotyped with the Illumina Bovine50K array, which includes 54,001 single nucleotide polymorphism (SNP) markers. The phenotypes used were de-regressed Australian breeding values (ABV) for protein yield, protein percentage, fat yield, fat percentage and milk yield. The breeding values were de-regressed to remove the contribution from relatives other than daughters [2]. All bulls had at least 80 daughters.
The following criteria and checks were applied to the bull's genotypes. Mendelian consistency checks revealed a small number of either sons discordant with their sires at many (>1000) SNP or sires with many discordant sons. These animals (17) were removed from the data set. In addition, we omitted bulls for which more than 20% of the genotypes were missing. One thousand, one hundred and eighty one Holstein and 364 Jersey bulls passed these criteria.
Criteria for selecting SNP were: less than 5% pedigree discordants (e.g. cases where a sire was homozygous for one allele and progeny were homozygous for the other allele), 90% call rate, MAF>2%, Hardy Weinberg P < 0.00001. Forty thousand and seventy seven SNP met all these criteria. All SNP which could not be mapped or were on the X chromosome were excluded from the final data set, leaving 39,048. Parentage checking was then performed again, and any genotype incompatible with the pedigree was set as missing.
To impute missing genotypes, the SNP were ordered by chromosome position, and the genotype calls and missing genotype information were submitted to fastPHASE chromosome by chromosome [8]. The genotypes were taken as those filled in by fastPHASE.
The Holstein reference (n = 781) and Jersey reference bulls (n = 287) were those progeny tested before 2004. The Holstein validation bulls were progeny tested during or after 2004 (n = 400), and the Jersey validation bulls were progeny tested after 2004 as well (n = 77).
Methods to predict GEBV
GBLUP
In a single breed population, if the number of QTL with effects normally distributed with a constant variance is high, then genomic selection is equivalent to replacing the expected relationship matrix with the genomic relationship matrix (G) estimated from DNA markers in the BLUP equations [9–14]. We assume a model

where y is a vector of phenotypes, μ is the mean, 1
n
is a vector of 1s, Z is a design matrix allocating records to breeding values, g is a vector of breeding values and e is a vector of random normal deviates ~  . Then g = Wu where u
j
is the effect of the jthSNP, and V(g) = WW'
. Then g = Wu where u
j
is the effect of the jthSNP, and V(g) = WW'  . Elements of matrix W are w
ij
for the ithanimal and jthSNP, where w
ij
= 0 - 2p
j
if the animal is homozygous 11 at the jthSNP, 1-2p
j
if the animal is heterozygous and 2 - 2p
j
if the animal is homozygous 22 at the jthSNP. The diagonal elements of WW' will be
. Elements of matrix W are w
ij
for the ithanimal and jthSNP, where w
ij
= 0 - 2p
j
if the animal is homozygous 11 at the jthSNP, 1-2p
j
if the animal is heterozygous and 2 - 2p
j
if the animal is homozygous 22 at the jthSNP. The diagonal elements of WW' will be  where m is the number of SNPs. If WW' is scaled such that
where m is the number of SNPs. If WW' is scaled such that  then
then  .
.
This is very similar to a previous definition of G except that it is rescaled so that the average of the diagonal elements is 1 [13]. Then breeding values for both phenotyped and non-phenotyped individuals can be predicted by solving the equations for model 1 above:

where G is the realised relationship matrix calculated as above, and  is a genetic variance.
is a genetic variance.
Variance components were estimated with ASREML [15]. The realised accuracy of GEBV was calculated as r(GEBV, ABV) where r(GEBV, ABV) was calculated in each validation population (Holstein and Jersey) separately, and ABV is the current Australian breeding value for bulls in the validation population. The expected accuracy of GEBV for the ithindividual was calculated from the standard error of the breeding value as  .
.
BayesA and BAYES_SSVS
We also compared r(GEBV, ABV) from GBLUP to approaches that estimate individual SNP effects and then calculate GEBV as the sum of these effects. The alternatives considered were BayesA and a Bayesian approach using stochastic search variable selection, BAYES_SSVS [1, 16]. BayesA makes a prior assumption that SNP effects are t-distributed, while BAYES_SSVS makes a prior assumption that a proportion π of the SNP effects are t-distributed and 1- π of the SNP effects have very close to zero [16]. Briefly, the model fitted in both BayesA and BAYES_SSVS was:

where y is a vector of n daughter yield deviations corrected for herd year season effects for each trait, X is (n × m) a design matrix allocating records to the marker effects with element X
ij
= 0, 1 or 2 if the genotype of animal i at SNP j is 11, 12 or 22 respectively. Vector u is a (m × 1) vector of SNP effects assumed normally distributed u
i
~ N(0,  ), e is a vector of random deviates where
), e is a vector of random deviates where  is the error variance, v
i
is the polygenic breeding value of the ithanimal, with variance A
is the error variance, v
i
is the polygenic breeding value of the ithanimal, with variance A , where A is the average relationship matrix. In BayesA and BAYES_SSVS the prior for
, where A is the average relationship matrix. In BayesA and BAYES_SSVS the prior for  was an inverse chi square distribution with 4.012 and 4.34 degrees of freedom, respectively. In BAYES_SSVS π was 0.05. Using the predicted SNP effects from each method, we predicted GEBV in the validation sets as
was an inverse chi square distribution with 4.012 and 4.34 degrees of freedom, respectively. In BAYES_SSVS π was 0.05. Using the predicted SNP effects from each method, we predicted GEBV in the validation sets as  .
.
Results and discussion
Genomic relationship between animals in reference and validation sets
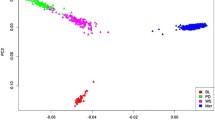
The genomic relationship matrix revealed a high level of relationship within the Holstein breed and within the Jersey breed, but very limited relationship between the breeds (Figure 1). Jersey individuals had a greater level of relationship within the breed than Holstein individuals, which is consistent with the higher inbreeding level for this breed [17]. The higher level of relationship could also reflect the fact that there were the number of animals in the Jersey reference population was smaller than that in the Holstein reference population, so the average allele frequency estimates used to modify W are closer to the Holstein allele frequencies.
Realised and expected accuracies from GBLUP
When GBLUP was applied only within a breed (Holstein reference only used to predict Holstein validation GEBV and likewise for Jersey), realised and expected accuracies were in reasonable agreement (Table 1) although the expected accuracies did over-predict the realised accuracies in Holsteins, by 8% overage across the traits. Results agreed better with the Jersey breed. GEBV accuracies can be compared to the accuracy of information available when the animals were born if the markers were not used. This is a breeding value computed from the individuals sire, maternal grandsire, and maternal grand sire breeding values from 2003, before the bulls in the validation data sets had any daughter information (this "sire pathway" breeding value is often used for selection because dam information may be missing or biased). GEBV accuracies were considerably higher than the accuracies of "sire pathway" breeding values for most traits.
It is important to note that the realised accuracy was calculated as r(GEBV, ABV) in the validation data set, which does not take into account the fact that the ABV have less than perfect correlation with true breeding values. The r(ABV, TBV) for the traits here was estimated as 0.92 by ADHIS. If the realised accuracies reported here are adjusted by this amount, the realised and expected accuracies for Holsteins are in better agreement. However, this adjustment may also bias the realised accuracies upwards, for example if the GEBV predicts the average relationship component of ABV more accurately than the component derived from individual SNP effects (eg Mendelian sampling). It has been demonstrated that breeding values predicted with GBLUP contain a considerable genetic relationship component [12].
When GBLUP was used to estimate GEBV using the combined (Holstein and Jersey) reference population, the realised accuracies of Jersey and Holstein GEBV were slightly higher for some traits than those obtained from the purebred reference populations (Table 2). However, agreement between realised and expected accuracies was weak with the expected accuracy over predicting considerably the realised accuracy.
Realised accuracies from BayesA and BAYES_SSVS
Our GBLUP results agreed with previous results in that when the Holstein SNP effects equations were used to predict Jersey GEBV, GEBV accuracies were close to zero, and likewise when SNP effects derived only from the Jersey reference population were used to predict Holstein GEBV (Table 3) [4]. The exception to this was fat percentage, where low to moderately accurate GEBV could be predicted for Jersey individuals from a Holstein reference and vice versa. This is likely because a QTL having a strong effect on fat percentage segregates in both breeds and the effect of the alleles on fat percentage follows the same direction in both breeds, and by coincidence the effects of the SNP associated with this polymorphism follow the same direction in both breeds [18]. With a Holstein only reference, Jersey GEBV from BayesA or Bayes_SSVS were more accurate than GBLUP GEBV. However, with a Jersey reference both the Bayesian methods and GBLUP gave similar (zero) accuracy of Holstein GEBV. The difference between these two results may reflect the small size of the Jersey reference population.
Using a combined Holstein Jersey reference population increased the accuracy of GEBV for both Holstein and Jersey individuals by up to 13% (for fat percentage) over that achieved with respective purebred reference populations when BayesA or BAYES_SSVS were used to predict SNP effects. When the combined reference population was used, GEBV accuracies for the Jersey validation set were higher from BayesA and BAYES_SSVS than from GBLUP for all traits except protein kg. GEBV accuracies of Holstein individuals were either the same or slightly lower compared with a pure Holstein reference population. There was very little difference in accuracy of GEBV from BayesA and BAYES_SSVS.
Predicting breeding values by replacing the expected additive relationship matrix with the genomic relationship in the usual BLUP equations is an attractive approach to implement genomic selection for two reasons. GEBV accuracies predicted in this way are the same as those from BLUP methods, which predict individual SNP effects since the models are equivalent [2, 3, 12, 13]. Furthermore, in the GBLUP approach, expected accuracies of breeding values are readily calculated from the diagonal elements of the inverse of the coefficient matrix. In populations of Holstein and Jersey bulls genotyped for approximately 50,000 markers, we have demonstrated that expected accuracies calculated in this way agree well with realised accuracies calculated from the correlation between GEBV and EBV in purebred populations. However when a multi-breed reference population was used the expected accuracy considerably over predicted the realised accuracy. Estimating  using a G derived from a multi-breed population is likely to result in an artificially high genetic variance. This is because the resulting estimate of
using a G derived from a multi-breed population is likely to result in an artificially high genetic variance. This is because the resulting estimate of  will be for a "base population" from which the breeds subsequently diverged. We did observe that estimates of
will be for a "base population" from which the breeds subsequently diverged. We did observe that estimates of  were higher when the multi-breed reference population was used than when either purebred reference populations were used. The estimate of
were higher when the multi-breed reference population was used than when either purebred reference populations were used. The estimate of  used to calculate the expected accuracies could be corrected for the inbreeding within in each breed subsequent to the base population. For Holstein individuals this value (calculated as twice the average off diagonal element in the genomic relationship matrix, for Holstein-Holstein elements) was 0.012 while for Jersey individuals it was 0.18. We recalculated the expected accuracies within each breed using
used to calculate the expected accuracies could be corrected for the inbreeding within in each breed subsequent to the base population. For Holstein individuals this value (calculated as twice the average off diagonal element in the genomic relationship matrix, for Holstein-Holstein elements) was 0.012 while for Jersey individuals it was 0.18. We recalculated the expected accuracies within each breed using  , where F
j
was 0.012 and 0.18 for Jerseys and Holsteins, respectively. This did reduce the expected accuracies, particularly for Jerseys but not to values comparable to the realised accuracies (Table 4). Another possibility is that the between-breed relationships are over-estimated due to inadequate marker density, resulting in inflation of the accuracy. This will be a topic for future research.
, where F
j
was 0.012 and 0.18 for Jerseys and Holsteins, respectively. This did reduce the expected accuracies, particularly for Jerseys but not to values comparable to the realised accuracies (Table 4). Another possibility is that the between-breed relationships are over-estimated due to inadequate marker density, resulting in inflation of the accuracy. This will be a topic for future research.
Our results demonstrate that using a reference population of one breed to predict GEBV of another breed gave low GEBV accuracies or equal to zero. However, combining reference individuals across a breed to form the reference populations resulted in accuracies of GEBV in purebred validation sets comparable or exceeding that achieved with a purebred reference population of the same breed. With BayesA and BAYES_SSVS, the accuracy of GEBV for most traits in the Jersey validation populations was greater when a multi-breed reference population was used than when a purebred Jersey population was used, by up to 13%. This suggests that for breeds with a small reference population, combining with other breeds to form a multi-breed reference is a possibility. Crossbred animals may also be useful candidates for the reference population. Indeed, a recent experiment demonstrated using a simulated population that a crossbreed reference population gave GEBV accuracies in selection candidates from contributing pure breed populations almost as high as from purebred reference populations of the same size [19]. Another study observed that using a combined Jersey Holstein reference population gave good GEBV accuracies in Holstein-Jersey cross bulls [4].
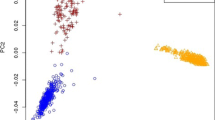
One hypothesis to explain the reasonable accuracy of GEBV in purebred candidates when a multi-breed reference population is used with BayesA or BAYES_SSVS to calculate SNP effects could be as follows. In order for an SNP to have an effect in a multi-breed reference population, it must be in LD with a QTL in both breeds, and given the extent of LD across breeds for this to occur the SNP must be very close to the QTL [5, 6]. Hence SNP that are in partial LD with a QTL in one breed are filtered, and only SNP in high LD with the QTL receive an effect in the prediction equation. This means that the SNP effect is more likely to persist across populations and generations, with as a result higher GEBV accuracies. Support for this hypothesis is given in Figure 2. DGAT1 is a gene on bovine chromosome 14 that harbours a mutation with a major effect on fat percentage in milk in Holstein and Jersey dairy cattle [18, 20]. In the Holstein population analysed in our work, the effect of this mutation is captured by two SNP, one very close to the gene, and one ~200 kb away. The SNP 200 kb from DGAT1 is in lower LD, but still has an effect. However, the SNP very close to DGAT1 is a better marker, with an effect likely to persist across populations and generations, because it is in such high LD with the mutation. Using a multi-breed reference population filters the SNP 200 kb from DGAT1, such that only the marker very close to the gene still has an effect. The above hypothesis is also supported in part by the results of Zhong et al. [21]. These authors have used simulated data to investigate factors affecting accuracy of genomic selection in populations derived from multiple inbred lines. In their simulations of a "multi-line" population, a method similar to BAYES_SSVS gave more accurate GEBV than other methods when the markers were in high LD with QTL of large effect, or when GEBV were predicted for selection candidates several generations removed from the reference population. Both these results suggest that in their "multi-line" population, their Bayesian method was able to identify SNPs in high LD with the QTL and use these in predicting GEBV.
Although BayesA and BAYES_SSVS resulted in GEBV with slightly higher realised accuracies than GBLUP when a multi-breed reference population was used, a drawback of these methods is that there is no obvious way to calculate expected accuracy of the breeding values obtained from these methods for selection candidates with no phenotype. In practise, the accuracy of GEBV from GBLUP may be close enough to those of BayesA and BAYES_SSVS, so that the Bayesian methods could be used to calculate SNP effects for predicting GEBV to maximise their accuracy, while expected and slightly conservative accuracies are calculated with GBLUP.
Our GEBV accuracies for the Jersey breed, even with a purebred Jersey reference population, were surprisingly high given the small size of the reference population. One explanation could be the low Ne of this breed and the high relationships in Figure 1 in the Jersey population) [17]. The Ne is one of the key parameters affecting the accuracy of genomic selection [14]. The lower the Ne, the smaller the number of independent chromosome segments for which effects must be estimated, which in turn leads to a higher GEBV accuracy. In fact the deterministic formula for GEBV accuracy predicts quite well the GEBV accuracies we achieve in the Jersey population given the Ne, number of records used and heritability [14, 22]. However the reader is reminded again of the small size of our validation set in the Jersey population.
A number of authors have demonstrated that combining pedigree EBV from large national data sets and marker derived breeding values gave more accurate GEBV than just using the marker derived information alone [2–4]. To calculate GEBV accuracies combining both pedigree and marker information, an index could be constructed reflecting the accuracies of both sources of information.
Conclusion
Predicting genomic breeding values using a genomic relationship matrix is an attractive approach to implement genomic selection, since accuracies of genomic breeding values can be calculated from the diagonal elements of the inverse of the coefficient matrix. Our results demonstrate that expected accuracies calculated in this way agree reasonably well with realised accuracies in purebred populations, but not in multi-breed populations. This indicates that the G matrix for multi-breed populations should be scaled in some way to achieve appropriate expected accuracies. Bayesian approaches that estimate individual SNP effects gave higher accuracies for some traits, particularly where there is a known mutation with a large effect on the trait segregating in the population. Finally, multi-breed reference populations could be a valuable resource for mapping QTL.
References
Meuwissen THE, Hayes BJ, Goddard ME: Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001, 157: 1819-1829.
VanRaden PM, Van Tassell CP, Wiggans GR, Sonstegard TS, Schnabel RD, Taylor JF, Schenkel F: Invited review: Reliability of genomic predictions for North American Holstein bulls. J Dairy Sci. 2009, 92: 16-24. 10.3168/jds.2008-1514.
Hayes BJ, Bowman PJ, Chamberlain AC, Goddard ME: Genomic selection in dairy cattle: progress and challenges. J Dairy Sci. 2009, 92: 1313-10.3168/jds.2008-1646.
Harris BL, Johnson DL, Spelman RJ: Genomic selection in New Zealand and the implications for national genetic evaluation. Proceedings of the Interbull Meeting, Niagara Falls, Canada. 2008
De Roos APW, Hayes BJ, Spelman R, Goddard ME: Linkage disequilibrium and persistence of phase in Holstein Friesian, Jersey and Angus cattle. Genetics. 2008, 179: 1503-1512. 10.1534/genetics.107.084301.
De Roos APW, Hayes BJ, Goddard ME: Reliability of genomic breeding values across multiple populations. Genetics. 2009,
Hickey JM, Veerkamp RF, Calus MP, Mulder HA, Thompson R: Estimation of prediction error variances via Monte Carlo sampling methods using different formulations of the prediction error variance. Genet Sel Evol. 2009, 41: 23-10.1186/1297-9686-41-23.
Scheet P, Stephens MA: A fast and flexible statistical model for large-scale population genotype data: Applications to inferring missing genotypes and haplotypic phase. Am J Hum Genet. 2006, 78: 629-644. 10.1086/502802.
Nejati-Javaremi A, Smith C, Gibson J: Effect of total allelic relationship on accuracy of evaluation and response to selection. J Anim Sci. 1997, 75: 1738-1745. inbreeding and maximising genetic gain. Genet Sel Evol 2007, 39:369-389
Villanueva B, Pong-Wong R, Fernandez J, Toro MA: Benefits from marker-assisted selection under an additive polygenic genetic model. J Anim Sci. 2005, 83: 1747-1752.
Fernando RL: Genetic evaluation and selection using genotypic, phenotypic and pedigree information. Proc. 6th Wld. Cong. Genet. App. Liv. Prod. 1998, 26: 329-336.
Habier D, Fernando RL, Dekkers JC: The impact of genetic relationship information on genome-assisted breeding values. Genetics. 2007, 177: 2389-2397.
VanRaden PM: Efficient methods to compute genomic predictions. J Dairy Sci. 2008, 91: 4414-4423. 10.3168/jds.2007-0980.
Goddard ME: Genomic selection: Prediction of accuracy and maximisation of long term response. Genetica. 2008, 136 (2): 245-257. 10.1007/s10709-008-9308-0.
Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R: ASReml User Guide Release 1.0. 2002, VSN International Ltd., Hemel Hempstead, UK
Verbyla KL, Hayes BJ, Bowman PJ, Goddard ME: Technical note: Accuracy of genomic selection using stochastic search variable selection in Australian Holstein Friesian dairy cattle. Genet Res. 2009,
Haile-Mariam M, Bowman P, Goddard ME: A practical approach for minimising inbreeding and maximising genetic gain in dairy cattle. Genet Sel Evol. 2007, 39 (4): 369-89. 10.1186/1297-9686-39-4-369.
Spelman RJ, Ford CA, McElhinney P, Gregory GC, Snell RG: Characterization of the DGAT1 gene in the New Zealand dairy population. J Dairy Sci. 2002, 85: 3514-3517.
Ibánez-Escriche N, Fernando RL, Toosi A, Dekkers JC: Genomic selection of purebreds for crossbred performance. Genet Sel Evol. 2009, 41: 12-10.1186/1297-9686-41-12.
Grisart BF, Farnir F, Karim L, Cambisano N, Kim JJ, Kvasz A, Mni M, Simon P, Frère JM, Coppieters W, Georges M: Genetic and functional confirmation of the causality of the DGAT1 K232A quantitative trait nucleotide in affecting milk yield and composition. Proc Natl Acad Sci USA. 2004, 24: 2398-2403. 10.1073/pnas.0308518100.
Zhong S, Dekkers JC, Fernando RL, Jannink JL: Factors affecting accuracy from genomic selection in populations derived from multiple inbred lines: a barley case study. Genetics. 2009, 182: 355-364. 10.1534/genetics.108.098277.
Hayes BJ, Visscher PM, Goddard ME: Increased accuracy of artificial selection by using the realized relationship matrix. Genet Res. 2009, 91: 47-60. 10.1017/S0016672308009981.
Acknowledgements
The authors are grateful to Curt van Tassell and Tad Sonstegard from the USDA for providing genotypes of Australian bulls, under a collaborative agreement between USDA and Department of Primary Industries Victoria.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
BJH wrote the paper and analysed the data, PJB analysed the data, ACC performed the lab work required, KV analysed the data, and MEG designed the experiment. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hayes, B.J., Bowman, P.J., Chamberlain, A.C. et al. Accuracy of genomic breeding values in multi-breed dairy cattle populations. Genet Sel Evol 41, 51 (2009). https://doi.org/10.1186/1297-9686-41-51
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1297-9686-41-51