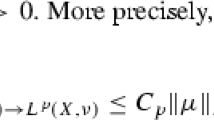Bilinear multipliers of weighted Wiener amalgam spaces and variable exponent Wiener amalgam spaces

Abstract

Let ${\omega }_1$, ${\omega }_2$ be slowly increasing weight functions, and let ${\omega }_3$ be any weight function on ${\mathbb{R}}^n$. Assume that $m(\xi ,\eta )$ is a bounded, measurable function on ${\mathbb{R}}^n\times {\mathbb{R}}^n$. We define

$$B_m(f,g)(x)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )m(\xi ,\eta )e^{2\pi i〈\xi +\eta ,x〉}d\xi d\eta$$

for all $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. We say that $m(\xi ,\eta )$ is a bilinear multiplier on ${\mathbb{R}}^n$ of type $(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$ if $B_m$ is a bounded operator from $W(L^{p_1},L_{{\omega }_1}^{q_1})\times W(L^{p_2},L_{{\omega }_2}^{q_2})$ to $W(L^{p_3},L_{{\omega }_3}^{q_3})$, where $1\le p_1\le q_1<\mathrm{\infty }$, $1\le p_2\le q_2<\mathrm{\infty }$, $1<p_3,q_3\le \mathrm{\infty }$. We denote by $BM(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$ the vector space of bilinear multipliers of type $(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$. In the first section of this work, we investigate some properties of this space and we give some examples of these bilinear multipliers. In the second section, by using variable exponent Wiener amalgam spaces, we define the bilinear multipliers of type $(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))$ from $W(L^{p_1(x)},L_{{\omega }_1}^{q_1})\times W(L^{p_2(x)},L_{{\omega }_2}^{q_2})$ to $W(L^{p_3(x)},L_{{\omega }_3}^{q_3})$, where $p_1^{\ast },p_2^{\ast },p_3^{\ast }<\mathrm{\infty }$, $p_1(x)\le q_1$, $p_2(x)\le q_2$, $1\le q_3\le \mathrm{\infty }$ for all $p_1(x),p_2(x),p_3(x)\in P({\mathbb{R}}^n)$. We denote by $BM(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))$ the vector space of bilinear multipliers of type $(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))$. Similarly, we discuss some properties of this space.

MSC:42A45, 42B15, 42B35.

1 Introduction

Throughout this paper we will work on ${\mathbb{R}}^n$ with Lebesgue measure dx. We denote by $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$, $C_c({\mathbb{R}}^n)$ and $S({\mathbb{R}}^n)$ the space of infinitely differentiable complex-valued functions with compact support on ${\mathbb{R}}^n$, the space of all continuous, complex-valued functions with compact support on ${\mathbb{R}}^n$ and the space of infinitely differentiable complex-valued functions on ${\mathbb{R}}^n$ that rapidly decrease at infinity, respectively. Let f be a complex-valued measurable function on ${\mathbb{R}}^n$. The translation, character and dilation operators $T_x$, $M_x$ and $D_s$ are defined by $T_{x}f(y)=f(y-x)$, $M_{x}f(y)=e^{2\pi i〈x,y〉}f(y)$ and $D_t^{p}f(y)=t^{-\frac{n}{p}}f(\frac{y}{t})$, respectively, for $x,y\in {\mathbb{R}}^n$, $0<p,t<\mathrm{\infty }$. With this notation out of the way, one has, for $1\le p\le \mathrm{\infty }$ and $\frac{1}{p}+\frac{1}{p^{\prime }}=1$,

$$(T_{x}f)\hat{\phantom{g}}(\xi )=M_{-x}\hat{f}(\xi ),(M_{x}f)\hat{\phantom{g}}(\xi )=T_x\hat{f}(\xi ),\left(D_t^{p}f\right)\hat{\phantom{g}}(\xi )=D_{t^{-1}}^{p^{\prime }}\hat{f}(\xi ).$$

For $1\le p\le \mathrm{\infty }$, $L^p({\mathbb{R}}^n)$ denotes the usual Lebesgue space. A continuous function ω satisfying $1\le \omega (x)$ and $\omega (x+y)\le \omega (x)\omega (y)$ for $x,y\in {\mathbb{R}}^n$ will be called a weight function on ${\mathbb{R}}^n$. If ${\omega }_1(x)\le {\omega }_2(x)$ for all $x\in {\mathbb{R}}^n$, we say that ${\omega }_1\le {\omega }_2$. For $1\le p\le \mathrm{\infty }$, we set

$$L_{\omega }^p\left({\mathbb{R}}^n\right)=\{f:f\omega \in L^p\left({\mathbb{R}}^n\right)\}.$$

It is known that $L_{\omega }^p({\mathbb{R}}^n)$ is a Banach space under the norm

$${\parallel f\parallel }_{p,\omega }={\parallel f\omega \parallel }_p={\left\{{\int }_{{\mathbb{R}}^n}\right|f(x)\omega (x){|}^{p}dx\}}^{\frac{1}{p}},1\le p<\mathrm{\infty }$$

or

$${\parallel f\parallel }_{\mathrm{\infty },\omega }={\parallel f\omega \parallel }_{\mathrm{\infty }}=\underset{x\in {\mathbb{R}}^n}{esssup}|f(x)\omega (x)|,p=\mathrm{\infty }.$$

The dual of the space $L_{\omega }^p({\mathbb{R}}^n)$ is the space $L_{{\omega }^{-1}}^q({\mathbb{R}}^n)$, where $\frac{1}{p}+\frac{1}{q}=1$ and ${\omega }^{-1}(x)=\frac{1}{\omega (x)}$. We say that a weight function ${\upsilon }_s$ is of polynomial type if ${\upsilon }_s(x)={(1+|x|)}^s$ for $s\ge 0$. Let f be a measurable function on ${\mathbb{R}}^n$. If there exist $C>0$ and $N\in \mathbb{N}$ such that

$$|f(x)|\le C{(1+x^2)}^N$$

for all $x\in {\mathbb{R}}^n$, then f is said to be a slowly increasing function [1]. It is easy to see that polynomial-type weight functions are slowly increasing. For $f\in L^1({\mathbb{R}}^n)$, the Fourier transform of f is denoted by $\hat{f}$. We know that $\hat{f}$ is a continuous function on ${\mathbb{R}}^n$ which vanishes at infinity and it has the inequality ${\parallel \hat{f}\parallel }_{\mathrm{\infty }}\le {\parallel f\parallel }_1$. We denote by $M({\mathbb{R}}^n)$ the space of bounded regular Borel measures, by $M(\omega )$ the space of μ in $M({\mathbb{R}}^n)$ such that

$${\parallel \mu \parallel }_{\omega }={\int }_{{\mathbb{R}}^n}\omega d|\mu |<\mathrm{\infty }.$$

If $\mu \in M({\mathbb{R}}^n)$, the Fourier-Stieltjes transform of μ is denoted by $\hat{\mu }$ [2].

The space ${(L^p({\mathbb{R}}^n))}_{\mathrm{loc}}$ consists of classes of measurable functions f on ${\mathbb{R}}^n$ such that $f{\chi }_K\in L^p({\mathbb{R}}^n)$ for any compact subset $K\subset {\mathbb{R}}^n$, where ${\chi }_K$ is the characteristic function of K. Let us fix an open set $Q\subset {\mathbb{R}}^n$ with compact closure and $1\le p,q\le \mathrm{\infty }$. The weighted Wiener amalgam space $W(L^p,L_{\omega }^q)$ consists of all elements $f\in {(L^p({\mathbb{R}}^n))}_{\mathrm{loc}}$ such that $F_f(z)={\parallel f{\chi }_{z+Q}\parallel }_p$ belongs to $L_{\omega }^q({\mathbb{R}}^n)$; the norm of $W(L^p,L_{\omega }^q)$ is ${\parallel f\parallel }_{W(L^p,L_{\omega }^q)}={\parallel F_f\parallel }_{q,\omega }$ [3–5].

In this paper, $P({\mathbb{R}}^n)$ denotes the family of all measurable functions $p:{\mathbb{R}}^n\to [1,\mathrm{\infty })$. We put

$$p_{\ast }=\underset{x\in {\mathbb{R}}^n}{essinf}p(x),p^{\ast }=\underset{x\in {\mathbb{R}}^n}{esssup}p(x).$$

We shall also use the notation

$${\mathrm{\Omega }}_{\mathrm{\infty }}=\{x\in {\mathbb{R}}^n:p(x)=\mathrm{\infty }\}.$$

The variable exponent Lebesgue spaces (or generalized Lebesgue spaces) $L^{p(x)}({\mathbb{R}}^n)$ are defined as the set of all (equivalence classes) measurable functions f on ${\mathbb{R}}^n$ such that ${\varrho }_p(\lambda f)<\mathrm{\infty }$ for some $\lambda >0$, equipped with the Luxemburg norm

$${\parallel f\parallel }_{p(x)}=inf\{\lambda >0:{\varrho }_p\left(\frac{f}{\lambda }\right)\le 1\}.$$

If $p^{\ast }<\mathrm{\infty }$, then $f\in L^{p(x)}({\mathbb{R}}^n)$ if ${\varrho }_p(f)<\mathrm{\infty }$. The set $L^{p(x)}({\mathbb{R}}^n)$ is a Banach space with the norm ${\parallel \cdot \parallel }_{p(x)}$. If $p(x)=p$ is a constant function, then the norm ${\parallel \cdot \parallel }_{p(x)}$ coincides with the usual Lebesgue norm ${\parallel \cdot \parallel }_p$ [6]. The spaces $L^{p(x)}({\mathbb{R}}^n)$ and $L^p({\mathbb{R}}^n)$ have many common properties. A crucial difference between $L^{p(x)}({\mathbb{R}}^n)$ and the classical Lebesgue spaces $L^p({\mathbb{R}}^n)$ is that $L^{p(x)}({\mathbb{R}}^n)$ is not invariant under translation in general. If $p^{\ast }<\mathrm{\infty }$, then $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in $L^{p(x)}({\mathbb{R}}^n)$. The space $L^{p(x)}({\mathbb{R}}^n)$ is a solid space, that is, if $f\in L^{p(x)}({\mathbb{R}}^n)$ is given and $g\in L_{\mathrm{loc}}^1({\mathbb{R}}^n)$ satisfies $|g(x)|\le |f(x)|$ a.e., then $g\in L^{p(x)}({\mathbb{R}}^n)$ and ${\parallel g\parallel }_{p(x)}\le {\parallel f\parallel }_{p(x)}$ by [6]. In this paper we will assume that $p^{\ast }<\mathrm{\infty }$.

The space ${(L^{p(x)}({\mathbb{R}}^n))}_{\mathrm{loc}}$ consists of classes of measurable functions f on ${\mathbb{R}}^n$ such that $f{\chi }_K\in L^{p(x)}({\mathbb{R}}^n)$ for any compact subset $K\subset {\mathbb{R}}^n$. Let us fix an open set $Q\subset {\mathbb{R}}^n$ with compact closure, $p(x)\in P({\mathbb{R}}^n)$ and $1\le q\le \mathrm{\infty }$. The variable exponent amalgam space $W(L^{p(x)},L_{\omega }^q)$ consists of all elements $f\in {(L^{p(x)}({\mathbb{R}}^n))}_{\mathrm{loc}}$ such that $F_f(z)={\parallel f{\chi }_{z+Q}\parallel }_{p(x)}$ belongs to $L_{\omega }^q({\mathbb{R}}^n)$; the norm of $W(L^{p(x)},L_{\omega }^q)$ is ${\parallel f\parallel }_{W(L^{p(x)},L_{\omega }^q)}={\parallel F_f\parallel }_{q,\omega }$ [7].

2 The bilinear multipliers space $BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$

Lemma 2.1 Let $1\le p\le q<\mathrm{\infty }$ and ω be a slowly increasing weight function. Then $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in the Wiener amalgam space $W(L^p,L_{\omega }^q)$.

Proof Since $\overline{C_c({\mathbb{R}}^n)}=L_{\omega }^q({\mathbb{R}}^n)$ [8], we have $\overline{C_c({\mathbb{R}}^n)}=W(L^p,L_{\omega }^q)$ by a lemma in [9]. Also we have the inclusion

$$C_c^{\mathrm{\infty }}\left({\mathbb{R}}^n\right)\subset C_c\left({\mathbb{R}}^n\right)\subset W(L^p,L_{\omega }^q).$$

For the proof that $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in $W(L^p,L_{\omega }^q)$, take any $f\in W(L^p,L_{\omega }^q)$. For given $\epsilon >0$, there exists $g\in C_c({\mathbb{R}}^n)$ such that

$${\parallel f-g\parallel }_{W(L^p,L_{\omega }^q)}<\frac{\epsilon }{2}.$$

(2.1)

Also, since $g\in C_c({\mathbb{R}}^n)\subset L_{\omega }^q({\mathbb{R}}^n)$ and $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in $L_{\omega }^q({\mathbb{R}}^n)$, by Lemma 2.1 in [10], there exists $h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ such that

$${\parallel g-h\parallel }_{q,\omega }<\frac{\epsilon }{2}.$$

Furthermore, by using the inequality $p\le q$, we write

$${\parallel g-h\parallel }_{W(L^p,L_{\omega }^q)}\le {\parallel g-h\parallel }_{q,\omega }<\frac{\epsilon }{2}$$

(2.2)

(see [11] and [5]). Combining (2.1) and (2.2), we obtain

$${\parallel f-h\parallel }_{W(L^p,L_{\omega }^q)}\le {\parallel f-g\parallel }_{W(L^p,L_{\omega }^q)}+{\parallel h-g\parallel }_{W(L^p,L_{\omega }^q)}<\epsilon .$$

This completes the proof. □

Definition 2.1 Let $1\le p_1\le q_1<\mathrm{\infty }$, $1\le p_2\le q_2<\mathrm{\infty }$, $1<p_3,q_3\le \mathrm{\infty }$ and ${\omega }_1$, ${\omega }_2$, ${\omega }_3$ be weight functions on ${\mathbb{R}}^n$. Assume that ${\omega }_1$, ${\omega }_2$ are slowly increasing functions and $m(\xi ,\eta )$ is a bounded, measurable function on ${\mathbb{R}}^n\times {\mathbb{R}}^n$. Define

$$B_m(f,g)(x)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )m(\xi ,\eta )e^{2\pi i〈\xi +\eta ,x〉}d\xi d\eta$$

for all $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$.

m is said to be a bilinear multiplier on ${\mathbb{R}}^n$ of type $(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$ if there exists $C>0$ such that

$${\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}$$

for all $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. That means that $B_m$ extends to a bounded bilinear operator from $W(L^{p_1},L_{{\omega }_1}^{q_1})\times W(L^{p_2},L_{\omega 2}^{q_2})$ to $W(L^{p_3},L_{{\omega }_3}^{q_3})$.

We denote by $BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ the space of all bilinear multipliers of type $(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$ and ${\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}=\parallel B_m\parallel$.

The following theorem is an example to a bilinear multiplier on ${\mathbb{R}}^n$ of type $(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$.

Theorem 2.1 Let $\frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{p_3}$, $\frac{1}{q_1}+\frac{1}{q_2}=\frac{1}{q_3}$ and ${\omega }_3\le {\omega }_1$. If $K\in L_{{\omega }_3}^1({\mathbb{R}}^n)$, then $m(\xi ,\eta )=\hat{K}(\xi -\eta )$ defines a bilinear multiplier and ${\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\parallel K\parallel }_{1,{\omega }_3}$.

Proof We know by Theorem 2.1 in [10] that for $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$,

$$B_m(f,g)(t)={\int }_{{\mathbb{R}}^n}f(t-y)g(t+y)K(y)dy.$$

(2.3)

Also by Proposition 11.4.1 in [5], $T_{y}f\in W(L^{p_1},L_{{\omega }_1}^{q_1})$, $T_{-y}g\in W(L^{p_2},L_{\omega 2}^{q_2})$. So, we write $F_{T_{y}f}\in L_{{\omega }_1}^{q_1}({\mathbb{R}}^n)$, $F_{T_{-y}g}\in L_{\omega 2}^{q_2}({\mathbb{R}}^n)$.

Using the Minkowski inequality and the generalized Hölder inequality, we have

$$\begin{array}{rcl}{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel {\parallel B_m(f,g){\chi }_{Q+x}\parallel }_{p_3}\parallel }_{q_3,{\omega }_3}\\ =& {\parallel {\parallel \{{\int }_{{\mathbb{R}}^n}f(t-y)g(t+y)K(y)dy\}{\chi }_{Q+x}\parallel }_{p_3}\parallel }_{q_3,{\omega }_3}\\ \le & {\int }_{{\mathbb{R}}^n}{\parallel {\parallel f(t-y)g(t+y){\chi }_{Q+x}(t)\parallel }_{p_3}\parallel }_{q_3,{\omega }_3}|K(y)|dy\\ \le & {\int }_{{\mathbb{R}}^n}{\parallel {\parallel f(t-y){\chi }_{Q+x}(t)\parallel }_{p_1}{\parallel g(t+y){\chi }_{Q+x}(t)\parallel }_{p_2}\parallel }_{q_3,{\omega }_3}|K(y)|dy\\ =& {\int }_{{\mathbb{R}}^n}{\parallel F_{T_{y}f}(x){\omega }_3(x)F_{T_{-y}g}(x)\parallel }_{q_3}|K(y)|dy.\end{array}$$

(2.4)

Again, by using Proposition 11.4.1 in [5] and the assumption ${\omega }_3\le {\omega }_1$, we write

$${\parallel F_{T_{y}f}{\omega }_3\parallel }_{q_1}\le {\omega }_3(y){\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}<\mathrm{\infty }.$$

(2.5)

From this result, we find $F_{T_{y}f}\in L_{{\omega }_3}^{q_1}({\mathbb{R}}^n)$. Hence by (2.4), (2.5) and the generalized Hölder inequality, we obtain

$$\begin{array}{rcl}{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& \le & {\int }_{{\mathbb{R}}^n}{\parallel F_{T_{y}f}(x){\omega }_3(x)\parallel }_{q_1}{\parallel F_{T_{-y}g}(x)\parallel }_{q_2}|K(y)|dy\\ \le & {\int }_{{\mathbb{R}}^n}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}|K(y)|{\omega }_3(y)dy\\ =& {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel K\parallel }_{1,{\omega }_3}\\ =& C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})},\end{array}$$

(2.6)

where $C={\parallel K\parallel }_{1,{\omega }_3}$. Then $m(\xi ,\eta )=\hat{K}(\xi -\eta )$ defines a bilinear multiplier. Finally, using (2.6), we obtain

$$\begin{array}{rcl}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}& =& \underset{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le 1,{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}\le 1}{sup}\frac{{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}}{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}}\\ \le & {\parallel K\parallel }_{1,{\omega }_3}.\end{array}$$

 □

Definition 2.2 Let $1\le p_1\le p_2<\mathrm{\infty }$, $1\le q_1\le q_2<\mathrm{\infty }$, $1<p_3,q_3\le \mathrm{\infty }$ and ${\omega }_1$, ${\omega }_2$, ${\omega }_3$ be weight functions on ${\mathbb{R}}^n$. Suppose that ${\omega }_1$, ${\omega }_2$ are slowly increasing functions. We denote by $\tilde{M}[(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ the space of measurable functions $M:{\mathbb{R}}^n\to \mathbb{C}$ such that $m(\xi ,\eta )=M(\xi -\eta )\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, that is to say,

$$B_M(f,g)(x)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )M(\xi -\eta )e^{2\pi i〈\xi +\eta ,x〉}d\xi d\eta$$

extends to a bounded bilinear map from $W(L^{p_1},L_{{\omega }_1}^{q_1})\times W(L^{p_2},L_{{\omega }_2}^{q_2})$ to $W(L^{p_3},L_{{\omega }_3}^{q_3})$. We denote ${\parallel M\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}=\parallel B_M\parallel$.

Let ω be a weight function. The continuous function ${\omega }^{-1}$ cannot be a weight function. But the following lemma can be proved easily by using the technique of the proof of Lemma 2.1.

Lemma 2.2 Let $1\le p\le q<\mathrm{\infty }$ and ω be a slowly increasing continuous weight function. Then $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in $W(L^p,L_{{\omega }^{-1}}^q)$ Wiener amalgam space.

Theorem 2.2 Let $\frac{1}{p_3}+\frac{1}{p_3^{\prime }}=1$, $\frac{1}{q_3}+\frac{1}{q_3^{\prime }}=1$, $q_3^{\prime }\ge p_3^{\prime }\ge 1$ and ${\omega }_3$ be a continuous, symmetric slowly increasing weight function. Then $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ if and only if there exists $C>0$ such that

$$|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\le C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }^{-1}}^{q_3^{\prime }})}$$

for all $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$.

Proof We assume that $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. By Theorem 2.2 in [10], we write, for all $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$,

$$\begin{array}{rcl}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |& =& |{\int }_{{\mathbb{R}}^n}h(y){\tilde{B}}_m(f,g)(y)dy|\\ \le & {\int }_{{\mathbb{R}}^n}|h(y)||{\tilde{B}}_m(f,g)(y)|dy,\end{array}$$

(2.7)

where ${\tilde{B}}_m(f,g)(y)=B_m(f,g)(-y)$. If we set $-t=u$, we have

$$\begin{array}{rcl}{\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel F_{{\tilde{B}}_m(f,g)}^Q\parallel }_{q_3,{\omega }_3}={\parallel {\parallel B_m(f,g)(u){\chi }_{Q+x}(-u)\parallel }_{p_3}\parallel }_{q_3,{\omega }_3}\\ =& {\parallel {\parallel B_m(f,g)(u){\chi }_{-Q-x}(u)\parallel }_{p_3}\parallel }_{q_3,{\omega }_3}={\parallel F_{B_m(f,g)}^{-Q}(-x)\parallel }_{q_3,{\omega }_3}.\end{array}$$

(2.8)

Since ${\omega }_3$ is a symmetric weight function, if we set $-x=y$, we have

$${\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}={\parallel F_{B_m(f,g)}^{-Q}(y)\parallel }_{q_3,{\omega }_3}.$$

(2.9)

We know from [3] and [5] that the definition of $W(L^{p_3},L_{{\omega }_3}^{q_3})$ is independent of the choice of Q. Then there exists $C>0$ such that

$${\parallel F_{B_m(f,g)}^{-Q}(y)\parallel }_{q_3,{\omega }_3}\le C_1{\parallel F_{B_m(f,g)}^Q(y)\parallel }_{q_3,{\omega }_3}.$$

(2.10)

Hence, by (2.9) and (2.10), we have

$${\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le C_1{\parallel F_{B_m(f,g)}^Q(y)\parallel }_{q_3,{\omega }_3}=C_1{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}.$$

(2.11)

Since from the assumption $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ the right-hand side of (2.11) is finite, thus ${\tilde{B}}_m(f,g)\in W(L^{p_3},L_{{\omega }_3}^{q_3})$. On the other hand, since $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, there exists $C_2>0$ such that

$${\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le C_2{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}.$$

(2.12)

Combining (2.11) and (2.12), we have

$${\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le C_1{C}_2{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}.$$

(2.13)

If we apply the Hölder inequality to the right-hand side of inequality (2.7) and use inequality (2.13), we obtain

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ \le {\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }^{-1}}^{q_3^{\prime }})}\hfill \\ \le C_1{C}_2{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}.\hfill \end{array}$$

For the proof of converse, assume that there exists a constant $C>0$ such that

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ \le C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}\hfill \end{array}$$

(2.14)

for all $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. From the assumption and (2.14), we write

$$|{\int }_{{\mathbb{R}}^n}h(y){\tilde{B}}_m(f,g)(y)dy|\le C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}.$$

(2.15)

Define a function ℓ from $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)\subset W(L^{p_3^{\prime }},L_{{\omega }^{-1}}^{q_3^{\prime }})$ to ℂ such that

$$\ell (h)={\int }_{{\mathbb{R}}^n}h(y){\tilde{B}}_m(f,g)(y)dy.$$

ℓ is linear and bounded by (2.15). Also, since $q_3^{\prime }\ge p_3^{\prime }\ge 1$, we have $\overline{C_c^{\mathrm{\infty }}({\mathbb{R}}^n)}=W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})$ by Lemma 2.2. Thus ℓ extends to a bounded function from $W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})$ to ℂ. Then $\ell \in {(W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }}))}^{\ast }=W(L^{p_3},L_{{\omega }_3}^{q_3})$. Again, since the definition of $W(L^{p_3},L_{{\omega }_3}^{q_3})$ is independent of the choice of Q, there exists $C_3>0$ such that

$${\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le C_3{\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}.$$

(2.16)

Combining (2.15) and (2.16), we obtain

$$\begin{array}{rcl}{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& \le & C_3{\parallel {\tilde{B}}_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\\ =& C_3\parallel \ell \parallel =C_3\underset{{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}\le 1}{sup}\frac{|\ell (h)|}{{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}}\\ \le & C_{3}C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}.\end{array}$$

This completes proof. □

The following theorem is a generalization of Theorem 2.1.

Theorem 2.3 Let $\frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{p_3}$, $\frac{1}{q_1}+\frac{1}{q_2}=\frac{1}{q_3}$, ${\omega }_3\le {\omega }_1$ and $\upsilon (x)=C{(1+x^2)}^N$, $C\ge 0$, $N\in \mathbb{N}$ be a weight function. If $\mu \in M(\upsilon )$ and $m(\xi ,\eta )=\hat{\mu }(\alpha \xi +\beta \eta )$ for $\alpha ,\beta \in \mathbb{R}$, then $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. Moreover,

$$\begin{array}{c}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\parallel \mu \parallel }_{\upsilon }\mathit{\text{if }}|\alpha |\le 1,\hfill \\ {\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le |\alpha {|}^{2N}{\parallel \mu \parallel }_{\upsilon }\mathit{\text{if }}|\alpha |>1.\hfill \end{array}$$

Proof Let $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. By Theorem 2.3 in [10], we have

$$B_m(f,g)(t)={\int }_{{\mathbb{R}}^n}f(t-\alpha y)g(t-\beta y)d\mu (y).$$

(2.17)

Also by [5] we write the inequalities

$${\parallel T_{\alpha y}f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le {\omega }_1(\alpha y){\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}$$

(2.18)

and

$${\parallel T_{\beta y}g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le {\omega }_2(\alpha y){\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}.$$

(2.19)

From these inequalities, we have $F_{T_{\alpha y}f}\in L_{{\omega }_1}^{q_1}({\mathbb{R}}^n)$ and $F_{T_{\beta y}g}\in L_{\omega 2}^{q_2}({\mathbb{R}}^n)$. If we use the inequality ${\omega }_3\le {\omega }_1$ and set $x-\alpha t=u$, we obtain

$${\parallel F_{T_{\alpha y}f}{\omega }_3\parallel }_{q_1}\le {\parallel F_{T_{\alpha y}f}{\omega }_1\parallel }_{q_1}\le {\omega }_1(\alpha y){\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})},$$

(2.20)

and hence $F_{T_{\alpha y}f}{\omega }_3\in L^{q_1}({\mathbb{R}}^n)$. Then by (2.17), (2.18), (2.19), (2.20) and the Hölder inequality, we have

$$\begin{array}{rcl}{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& \le & {\parallel {\int }_{{\mathbb{R}}^n}{\parallel f(t-\alpha y)g(t-\beta y){\chi }_{Q+x}(t)\parallel }_{p_3}d|\mu |(y)\parallel }_{q_3,{\omega }_3}\\ \le & {\parallel {\int }_{{\mathbb{R}}^n}{\parallel f(t-\alpha y){\chi }_{Q+x}(t)\parallel }_{p_1}{\parallel g(t-\beta y){\chi }_{Q+x}(t)\parallel }_{p_2}d|\mu |(y)\parallel }_{q_3,{\omega }_3}\\ \le & {\int }_{{\mathbb{R}}^n}{\parallel F_{T_{\alpha y}f}(x)F_{T_{\beta y}g}(x)\parallel }_{q_3,{\omega }_3}d|\mu |(y)\\ \le & {\int }_{{\mathbb{R}}^n}{\parallel F_{T_{\alpha y}f}(x){\omega }_3(x)\parallel }_{q_1}{\parallel F_{T_{\beta y}g}(x)\parallel }_{q_2}d|\mu |(y)\\ \le & {\int }_{{\mathbb{R}}^n}{\omega }_1(\alpha y){\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L^{q_2})}d|\mu |(y)\\ \le & {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}{\int }_{{\mathbb{R}}^n}{\omega }_1(\alpha y)d|\mu |(y).\end{array}$$

(2.21)

Now, suppose that $\alpha \le 1$. Since ${\omega }_1$ is a slowly increasing weight function, there exist $C\ge 0$ and $N\in \mathbb{N}$ such that

$${\omega }_1(x)\le C{(1+x^2)}^N=\upsilon (x).$$

Then

$${\int }_{{\mathbb{R}}^n}{\omega }_1(\alpha y)d|\mu |(y)\le {\int }_{{\mathbb{R}}^n}C{(1+{\alpha }^2{y}^2)}^{N}d|\mu |(y)\le {\int }_{{\mathbb{R}}^n}C{(1+y^2)}^{N}d|\mu |(y)={\parallel \mu \parallel }_{\upsilon }.$$

Hence by (2.21)

$${\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}{\parallel \mu \parallel }_{\upsilon }.$$

(2.22)

Thus $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, and by (2.22) we obtain

$$\begin{array}{rl}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}& =\underset{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le 1,{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le 1}{sup}\frac{{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}}{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}}\\ \le {\parallel \mu \parallel }_{\upsilon }.\end{array}$$

Similarly, if $\alpha >1$, then

$${\int }_{{\mathbb{R}}^n}{\omega }_1(\alpha y)d|\mu |(y)\le {\int }_{{\mathbb{R}}^n}C{({\alpha }^2+{\alpha }^2{y}^2)}^{N}d|\mu |(y)={\alpha }^{2N}{\int }_{{\mathbb{R}}^n}\upsilon (y)d|\mu |(y)={\alpha }^{2N}{\parallel \mu \parallel }_{\upsilon }.$$

Therefore by (2.21) we have

$${\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\le {\alpha }^{2N}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}{\parallel \mu \parallel }_{\upsilon }.$$

(2.23)

Hence, we obtain $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, and by (2.23)

$$\begin{array}{rcl}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}& =& \underset{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le 1,{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le 1}{sup}\frac{{\parallel B_m(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}}{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}}\\ \le & {\alpha }^{2N}{\parallel \mu \parallel }_{\upsilon }.\end{array}$$

 □

Now, we will give some properties of the space $BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$.

Theorem 2.4 Let $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$.

• (a) $T_{({\xi }_0,{\eta }_0)}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ for each $({\xi }_0,{\eta }_0)\in {\mathbb{R}}^{2n}$ and

  $${\parallel T_{({\xi }_0,{\eta }_0)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}={\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.$$

• (b) $M_{({\xi }_0,{\eta }_0)}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ for each $({\xi }_0,{\eta }_0)\in {\mathbb{R}}^{2n}$ and

  $$\begin{array}{c}{\parallel M_{({\xi }_0,{\eta }_0)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\hfill \\ \le {\omega }_1(-{\xi }_0){\omega }_2(-{\eta }_0){\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.\hfill \end{array}$$

Proof (a) Let $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. From Theorem 2.4 in [10], we write the equality

$$B_{T_{({\xi }_0,{\eta }_0)}m}(f,g)(x)=e^{2\pi i〈{\xi }_0+{\eta }_0,x〉}{B}_m(M_{-{\xi }_0}f,M_{-{\eta }_0}g)(x).$$

(2.24)

Also the equalities ${\parallel M_{-{\xi }_0}f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}={\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}$ and ${\parallel M_{-{\eta }_0}g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}={\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}$ are satisfied. Then, using equality (2.24) and the assumption $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, we have

$$\begin{array}{rcl}{\parallel B_{T_{({\xi }_0,{\eta }_0)}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel e^{2\pi i〈{\xi }_0+{\eta }_0,x〉}{B}_m(M_{-{\xi }_0}f,M_{-{\eta }_0}g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\\ =& {\parallel B_m(M_{-{\xi }_0}f,M_{-{\eta }_0}g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\\ \le & C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\end{array}$$

for some $C>0$. Thus $T_{({\xi }_0,{\eta }_0)}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. Moreover, we obtain

$$\begin{array}{c}{\parallel T_{({\xi }_0,{\eta }_0)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\hfill \\ =\parallel B_{T_{({\xi }_0,{\eta }_0)}m}\parallel =\underset{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le 1,{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le 1}{sup}\frac{{\parallel B_{T_{({\xi }_0,{\eta }_0)}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}}{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}}\hfill \\ =\underset{{\parallel M_{-{\xi }_0}f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le 1,{\parallel M_{-{\eta }_0}g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le 1}{sup}\frac{{\parallel B_{T_{({\xi }_0,{\eta }_0)}m}(M_{-{\xi }_0}f,M_{-{\eta }_0}g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}}{{\parallel M_{-{\xi }_0}f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel M_{-{\eta }_0}g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}}\hfill \\ =\parallel B_m\parallel ={\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.\hfill \end{array}$$

(b) For any $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$, we write

$$B_{M_{({\xi }_0,{\eta }_0)}m}(f,g)(x)=B_m(T_{-{\xi }_0}f,T_{-{\eta }_0}g)(x)$$

(2.25)

by Theorem 2.4 in [10]. Also, the inequalities ${\parallel T_{-{\xi }_0}f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le {\omega }_1(-{\xi }_0){\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}$ and ${\parallel T_{-{\eta }_0}g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le {\omega }_2(-{\eta }_0){\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}$ are satisfied [5]. Since $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, by (2.25) we have

$$\begin{array}{rcl}{\parallel B_{M_{({\xi }_0,{\eta }_0)}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel B_m(T_{-{\xi }_0}f,T_{-{\eta }_0}g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\\ \le & \parallel B_m\parallel {\parallel T_{-{\xi }_0}f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel T_{-{\eta }_0}g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\\ \le & {\omega }_1(-{\xi }_0){\omega }_2(-{\eta }_0)\parallel B_m\parallel {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\end{array}$$

(2.26)

and hence $M_{({\xi }_0,{\eta }_0)}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. So, by (2.26) we obtain

$$\begin{array}{c}{\parallel M_{({\xi }_0,{\eta }_0)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\hfill \\ =\underset{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le 1,{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\le 1}{sup}\frac{{\parallel B_{M_{({\xi }_0,{\eta }_0)}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}}{{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}}\hfill \\ \le {\omega }_1(-{\xi }_0){\omega }_2(-{\eta }_0)\parallel B_m\parallel ={\omega }_1(-{\xi }_0){\omega }_2(-{\eta }_0){\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.\hfill \end{array}$$

 □

Lemma 2.3 If ω is a slowly increasing weight function such that $\omega (x)\le C_1{(1+x^2)}^N=\upsilon (x)$ and $f\in W(L^p,L_{\omega }^q)$, then $D_y^{p}f\in W(L^p,L_{\upsilon }^q)$. Moreover,

$$\begin{array}{c}{\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}\le C{\parallel f\parallel }_{W(L^p,L_{\upsilon }^q)}\mathit{\text{if }}y\le 1,\hfill \\ {\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}<C{y}^{\frac{n}{q}+2N}{\parallel f\parallel }_{W(L^p,L_{\upsilon }^q)}\mathit{\text{if }}y>1\hfill \end{array}$$

for some $C>0$.

Proof Take any $f\in W(L^p,L_{\omega }^q)$. If we get $\frac{t}{y}=u$, we obtain

$$\begin{array}{rcl}{\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}& =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|D_y^{p}f(t){\chi }_{Q+x}(t){|}^{p}dt\}}^{\frac{1}{p}}\parallel }_{q,\omega }\\ =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|y^{-\frac{n}{p}}f\left(\frac{t}{y}\right){|}^p{\chi }_{Q+x}(t)dt\}}^{\frac{1}{p}}\parallel }_{q,\omega }\\ =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|f(u){|}^p{\chi }_{y^{-1}Q+y^{-1}x}(u)du\}}^{\frac{1}{p}}\parallel }_{q,\omega }\\ =& {\parallel F_f^{y^{-1}Q}\left(y^{-1}x\right)\parallel }_{q,\omega }.\end{array}$$

(2.27)

Again, if we say $y^{-1}x=s$ and use ω to be slowly increasing, then there exist $C_1>0$ and $N\in \mathbb{N}$ such that

$$\begin{array}{rcl}{\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}& =& {\left\{{\int }_{{\mathbb{R}}^n}\right|F_f^{y^{-1}Q}\left(y^{-1}x\right){|}^q\omega {(x)}^{q}dx\}}^{\frac{1}{q}}\\ =& y^{\frac{n}{q}}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_f^{y^{-1}Q}(s){|}^q\omega {(ys)}^{q}ds\}}^{\frac{1}{q}}\\ \le & y^{\frac{n}{q}}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_f^{y^{-1}Q}(s){|}^q{\left(C_1{(1+y^2{s}^2)}^N\right)}^{q}ds\}}^{\frac{1}{q}}\end{array}$$

(2.28)

by equation (2.27).

Let $y\le 1$. Using inequality (2.28), we have

$${\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}\le {\left\{{\int }_{{\mathbb{R}}^n}\right|F_f^{y^{-1}Q}(s){|}^q{\left(C_1{(1+s^2)}^N\right)}^{q}ds\}}^{\frac{1}{q}}={\parallel F_f^{y^{-1}Q}\parallel }_{q,\upsilon }.$$

(2.29)

Since $y^{-1}Q$ is a compact set and the definition of $W(L^p,L_{\upsilon }^q)$ is independent of the choice of a compact set Q, then there exists $C>0$ such that

$${\parallel F_f^{y^{-1}Q}\parallel }_{q,\upsilon }\le C{\parallel F_f^Q\parallel }_{q,\upsilon }$$

(2.30)

by [3, 5]. Then by (2.29) we write

$${\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}\le {\parallel F_f^{y^{-1}Q}\parallel }_{q,\upsilon }\le C{\parallel F_f^Q\parallel }_{q,\upsilon }=C{\parallel f\parallel }_{W(L^p,L_{\upsilon }^q)}.$$

Thus we have $D_y^{p}f\in W(L^p,L_{\upsilon }^q)$.

Now, assume that $y>1$. Similarly, by (2.28) and (2.30), we get

$$\begin{array}{rcl}{\parallel D_y^{p}f\parallel }_{W(L^p,L_{\omega }^q)}& <& y^{\frac{n}{q}}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_f^{y^{-1}Q}(s){|}^q{\left(C_1{(y^2+y^2{s}^2)}^N\right)}^{q}ds\}}^{\frac{1}{q}}\\ =& y^{\frac{n}{q}+2N}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_f^{y^{-1}Q}(s){|}^q\upsilon {(s)}^{q}ds\}}^{\frac{1}{q}}\\ \le & y^{\frac{n}{q}+2N}{\parallel f\parallel }_{W(L^p,L_{\upsilon }^q)}.\end{array}$$

Hence $D_y^{p}f\in W(L^p,L_{\upsilon }^q)$. □

Theorem 2.5 Let ${\upsilon }_i(x)=C_i{(1+x^2)}^{N_i}$, $C_i>0$, $N_i>0$ for $i=1,2,3$, and let ${\omega }_3$ be a slowly increasing weight function. If $\frac{2}{q}=\frac{1}{p_1}+\frac{1}{p_2}-\frac{1}{p_3}$, $0<y<\mathrm{\infty }$ and $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3)]$, then $D_y^{q}m\in BM[W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3)]$. Moreover, then

$$\begin{array}{c}{\parallel D_y^{q}m\parallel }_{(W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3))}\hfill \\ \le C{y}^{-\frac{n}{q_3}-2N_3}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3))}\mathit{\text{if }}y\le 1,\hfill \\ {\parallel D_y^{q}m\parallel }_{(W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3))}\hfill \\ <C{y}^{\frac{n}{q_1}+\frac{n}{q_2}+2N_1+2N_2}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3))}\mathit{\text{if }}y>1.\hfill \end{array}$$

Proof Let $f\in W(L^{p_1},L_{{\omega }_1}^{q_1})$ and $g\in W(L^{p_2},L_{{\omega }_2}^{q_2})$ be given. From Lemma 2.3, we have $D_y^{p_1}f\in W(L^{p_1},L_{{\omega }_1}^{q_1})$ and $D_y^{p_2}g\in W(L^{p_2},L_{{\omega }_2}^{q_2})$. Also it is known by Theorem 2.5 in [10] that

$$B_{D_y^{q}m}(f,g)(y)=D_{y^{-1}}^{p_3}{B}_m(D_y^{p_1}f,D_y^{p_2}g)(y).$$

If we use this equality, we write

$$\begin{array}{rcl}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|D_{y^{-1}}^{p_3}{B}_m(D_y^{p_1}f,D_y^{p_2}g)(t){\chi }_{Q+x}(t){|}^{p_3}dt\}}^{\frac{1}{p_3}}\parallel }_{q_3,{\omega }_3}\\ =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|y^{\frac{n}{p_3}}{B}_m(D_y^{p_1}f,D_y^{p_2}g)\left(\frac{t}{y^{-1}}\right){\chi }_{Q+x}(t){|}^{p_3}dt\}}^{\frac{1}{p_3}}\parallel }_{q_3,{\omega }_3}\\ =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}{y}^n\right|B_m(D_y^{p_1}f,D_y^{p_2}g)(ty){\chi }_{Q+x}(t){|}^{p_3}dt\}}^{\frac{1}{p_3}}\parallel }_{q_3,{\omega }_3}.\end{array}$$

If we say $yt=u$ in the last equality, we have

$$\begin{array}{rcl}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|B_m(D_y^{p_1}f,D_y^{p_2}g)(u){\chi }_{yQ+yx}(u){|}^{p_3}dt\}}^{\frac{1}{p_3}}\parallel }_{q_3,{\omega }_3}\\ =& {\parallel F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}(yx)\parallel }_{q_3,{\omega }_3}.\end{array}$$

(2.31)

On the other hand, since ${\omega }_3$ is a slowly increasing weight function, there exist $C_3>0$, $N_3>0$ such that ${\omega }_3(x)\le C_3{(1+x^2)}^{N_3}={\upsilon }_3(x)$. If we make the substitution $yx=s$ in equality (2.31), we obtain

$$\begin{array}{rcl}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& =& {\parallel F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}(yx)\parallel }_{q_3,{\omega }_3}\\ =& {\left\{{\int }_{{\mathbb{R}}^n}\right|F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}(s){|}^{q_3}{\omega }_3{\left(y^{-1}s\right)}^{q_3}{y}^{-n}ds\}}^{\frac{1}{q_3}}\\ =& y^{-\frac{n}{q_3}}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}(s){|}^{q_3}{\omega }_3{\left(y^{-1}s\right)}^{q_3}ds\}}^{\frac{1}{q_3}}\\ \le & y^{-\frac{n}{q_3}}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}(s){|}^{q_3}{\left(C_3{(1+y^{-2}{s}^2)}^{N_3}\right)}^{q_3}ds\}}^{\frac{1}{q_3}}.\end{array}$$

We assume that $y\le 1$. Then

$$\begin{array}{rcl}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& \le & y^{-\frac{n}{q_3}}{\left\{{\int }_{{\mathbb{R}}^n}\right|F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}(s){|}^{q_3}{\left(C_3{(y^{-2}+y^{-2}{s}^2)}^{N_3}\right)}^{q_3}ds\}}^{\frac{1}{q_3}}\\ =& y^{-\frac{n}{q_3}-2N_3}{\parallel F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^{yQ}\parallel }_{q_3,{\upsilon }_3}.\end{array}$$

Also, since yQ is a compact set, we have

$$\begin{array}{rcl}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& \le & C{y}^{-\frac{n}{q_3}-2N_3}{\parallel F_{B_m(D_y^{p_1}f,D_y^{p_2}g)}^Q\parallel }_{q_3,{\upsilon }_3}\\ =& C{y}^{-\frac{n}{q_3}-2N_3}{\parallel B_m(D_y^{p_1}f,D_y^{p_2}g)\parallel }_{W(L^{p_3},L_{{\upsilon }_3}^{q_3})}.\end{array}$$

(2.32)

Since $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3)]$, by Lemma 2.3 and inequality (2.32), we obtain

$$\begin{array}{c}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ \le C{y}^{-\frac{n}{q_3}-2N_3}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3))}{\parallel f\parallel }_{W(L^{p_1},L_{{\upsilon }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\upsilon }_2}^{q_2})}.\hfill \end{array}$$

(2.33)

Then $D_y^{q}m\in BM[W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3)]$, and by (2.33) we have

$${\parallel D_y^{q}m\parallel }_{(W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3))}\le C{y}^{-\frac{n}{q_3}-2N_3}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3))}.$$

Now let $y>1$. Again, since $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3)]$, by Lemma 2.3 and inequality (2.32), we obtain

$$\begin{array}{c}{\parallel B_{D_y^{q}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ <C{\parallel B_m(D_y^{p_1}f,D_y^{p_2}g)\parallel }_{W(L^{p_3},L_{{\upsilon }_3}^{q_3})}\hfill \\ <C{y}^{\frac{n}{q_1}+\frac{n}{q_2}+2N_1+2N_2}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3))}{\parallel f\parallel }_{W(L^{p_1},L_{{\upsilon }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\upsilon }_2}^{q_2})}.\hfill \end{array}$$

(2.34)

Thus $D_y^{q}m\in BM[W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3)]$, and by (2.34) we have

$${\parallel D_y^{q}m\parallel }_{(W(p_1,q_1,{\upsilon }_1;p_2,q_2,{\upsilon }_2;p_3,q_3,{\omega }_3))}<C{y}^{\frac{n}{q_1}+\frac{n}{q_2}+2N_1+2N_2}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\upsilon }_3))}.$$

 □

Theorem 2.6 Let $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$.

• (a) If $\mathrm{\Phi }\in L^1({\mathbb{R}}^{2n})$, then $\mathrm{\Phi }\ast m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ and

  $${\parallel \mathrm{\Phi }\ast m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\parallel \mathrm{\Phi }\parallel }_1{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.$$

• (b) If $\mathrm{\Phi }\in L_{\omega }^1({\mathbb{R}}^{2n})$ such that $\omega (u,\upsilon )={\omega }_1(u){\omega }_2(\upsilon )$, then $\hat{\mathrm{\Phi }}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ and

  $${\parallel \hat{\mathrm{\Phi }}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\parallel \mathrm{\Phi }\parallel }_{1,\omega }{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.$$

Proof (a) Let $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ be given. By Proposition 2.5 in [12]

$$B_{\mathrm{\Phi }\ast m}(f,g)(y)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\mathrm{\Phi }(u,v)B_{T_{(u,v)}m}(f,g)(y)dudv.$$

If we use Theorem 2.4 and the assumption $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, we have

$$\begin{array}{c}{\parallel B_{\mathrm{\Phi }\ast m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ \le {\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}{\parallel \mathrm{\Phi }(u,v)B_{T_{(u,v)}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}dudv\hfill \\ \le {\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\mathrm{\Phi }(u,v)|{\parallel T_{(u,v)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}dudv\hfill \\ ={\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}{\parallel \mathrm{\Phi }\parallel }_1{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}<\mathrm{\infty }.\hfill \end{array}$$

(2.35)

Hence $\mathrm{\Phi }\ast m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, and by (2.35) we obtain

$${\parallel \mathrm{\Phi }\ast m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\parallel \mathrm{\Phi }\parallel }_1{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.$$

(b) Let $\mathrm{\Phi }\in L_{\omega }^1({\mathbb{R}}^{2n})$. Take any $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. It is known by Proposition 2.5 in [12] that

$$B_{\hat{\mathrm{\Phi }}m}(f,g)(x)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\mathrm{\Phi }(u,v)B_{M_{(-u,-v)}m}(f,g)(x)dudv.$$

Since $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, we have $M_{(-u,-v)}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ and

$${\parallel M_{(-u,-v)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\omega }_1(u){\omega }_2(v){\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}$$

by Theorem 2.4. Then

$$\begin{array}{c}{\parallel B_{\hat{\mathrm{\Phi }}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ \le {\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}{\parallel \mathrm{\Phi }(u,v)B_{M_{(-u,-v)}m}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}dudv\hfill \\ \le {\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\mathrm{\Phi }(u,v)|{\parallel M_{(-u,-v)}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}{\parallel f\parallel }_{p_1,{\omega }_1}{\parallel g\parallel }_{p_2,{\omega }_2}dudv\hfill \\ \le {\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\mathrm{\Phi }(u,v)|{\omega }_1(u){\omega }_2(\upsilon ){\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\hfill \\ \times {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}dudv\hfill \\ ={\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel \mathrm{\Phi }\parallel }_{1,\omega }.\hfill \end{array}$$

(2.36)

Thus from (2.36) we obtain $\hat{\mathrm{\Phi }}m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ and

$${\parallel \hat{\mathrm{\Phi }}m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\le {\parallel \mathrm{\Phi }\parallel }_{1,\omega }{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}.$$

 □

Theorem 2.7 Let $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. If $Q_1$, $Q_2$ are bounded measurable sets in ${\mathbb{R}}^n$, then

$$\begin{array}{rcl}h(\xi ,\eta )& =& \frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}m(\xi +u,\eta +v)dudv\\ \in & BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)].\end{array}$$

Proof Let $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. We know by Theorem 2.9 in [10] that

$$B_h(f,g)(x)=\frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{B}_{T_{(-u,-v)m}}(f,g)(x)dudv.$$

From Theorem 2.4, we have

$$\begin{array}{c}{\parallel B_h(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ \le \frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{\parallel B_{T_{(-u,-v)m}}(f,g)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}dudv\hfill \\ \le \frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{\parallel T_{(-u,-v)m}\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\hfill \\ \times {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}dudv\hfill \\ =\frac{1}{\mu (Q_1\times Q_2)}{\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}\hfill \\ \times {\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}\mu (Q_1\times Q_2)\hfill \\ ={\parallel m\parallel }_{(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}.\hfill \end{array}$$

Hence, we obtain $h(\xi ,\eta )\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. □

Theorem 2.8 Let ${\omega }_3$ be a continuous, symmetric, slowly increasing weight function, $\omega (u,v)={\omega }_1(u){\omega }_2(v)$, ${\omega }_3\le {\omega }_1$, $\frac{1}{q_1}+\frac{1}{q_2}=\frac{1}{q_3}$, $\frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{p_3}$, $\frac{1}{p_3}+\frac{1}{p_3^{\prime }}=1$, $\frac{1}{q_3}+\frac{1}{q_3^{\prime }}=1$ and $q_3^{\prime }\ge p_3^{\prime }$. Assume that $\mathrm{\Phi }\in L_{\omega }^1({\mathbb{R}}^{2n})$, ${\mathrm{\Psi }}_1\in L_{{\omega }_1}^1({\mathbb{R}}^n)$ and ${\mathrm{\Psi }}_2\in L_{{\omega }_2}^1({\mathbb{R}}^n)$. If $m(\xi ,\eta )={\hat{\mathrm{\Psi }}}_1(\xi )\hat{\mathrm{\Phi }}(\xi ,\eta ){\hat{\mathrm{\Psi }}}_2(\eta )$, then $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$.

Proof Take any $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. Then, by Theorem 2.10 in [10], we write

$$|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\le {\int }_{{\mathbb{R}}^n}|h(y){\tilde{B}}_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)(y)|dy.$$

On the other hand, we know that the inequalities

$${\parallel f\ast {\mathrm{\Psi }}_1\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}\le C_1{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel {\mathrm{\Psi }}_1\parallel }_{1,{\omega }_1}$$

(2.37)

and

$${\parallel g\ast {\mathrm{\Psi }}_2\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}\le C_2{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel {\mathrm{\Psi }}_2\parallel }_{1,{\omega }_2}$$

(2.38)

hold, where $C_1>0$, $C_2>0$ by [3]. That means $f\ast {\mathrm{\Psi }}_1\in W(L^{p_1},L_{{\omega }_1}^{q_1})$ and $g\ast {\mathrm{\Psi }}_2\in W(L^{p_2},L_{{\omega }_2}^{q_2})$. Also, every constant function is bilinear multiplier of type $(W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3))$ under the given conditions. So, by Theorem 2.6, we have $\hat{\mathrm{\Phi }}\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. Now, if we say that $-y=u$, we have

$$\begin{array}{c}{\parallel {\tilde{B}}_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)(y)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ ={\parallel {\left\{{\int }_{{\mathbb{R}}^n}\right|B_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)(u){|}^{p_3}{\chi }_{-Q-x}(u)du\}}^{\frac{1}{p_3}}\parallel }_{q_3,{\omega }_3}\hfill \\ ={\parallel F_{B_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)}^{-Q}(-x)\parallel }_{q_3,{\omega }_3}.\hfill \end{array}$$

In this here, we set $-x=u$ and use ${\omega }_3$ to be symmetric. Then we have

$$\begin{array}{rcl}{\parallel {\tilde{B}}_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)(y)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}& \le & C_3{\parallel F_{B_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)}^Q\parallel }_{q_3,{\omega }_3}\\ =& C_3{\parallel B_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\end{array}$$

(2.39)

by [5]. Using the Hölder inequality, inequalities (2.37), (2.38), (2.39) and $\hat{\mathrm{\Phi }}\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$, we find

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ \le {\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}{\parallel B_{\hat{\mathrm{\Phi }}}(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)\parallel }_{W(L^{p_3},L_{{\omega }_3}^{q_3})}\hfill \\ \le C_1{C}_2{C}_3{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}\parallel B_{\hat{\mathrm{\Phi }}}\parallel {\parallel {\mathrm{\Psi }}_1\parallel }_{1,{\omega }_1}{\parallel {\mathrm{\Psi }}_2\parallel }_{1,{\omega }_2}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}.\hfill \end{array}$$

If we say $C=C_1{C}_2{C}_3\parallel B_{\hat{\mathrm{\Phi }}}\parallel {\parallel {\mathrm{\Psi }}_1\parallel }_{1,{\omega }_1}{\parallel {\mathrm{\Psi }}_2\parallel }_{1,{\omega }_2}$, then we obtain

$$|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\le C{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{{\omega }_2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}.$$

From Theorem 2.2, we have $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. □

Theorem 2.9 Let $1\le p_1,p_2\le p\le 2$, $1\le q_1,q_2\le r\le 2$, $p_3\ge p^{\prime }$, $q_3\ge r^{\prime }$ and $q_3^{\prime }\ge p_3^{\prime }$ such that $\frac{1}{p_3}=\frac{1}{p_1}+\frac{1}{p_2}-\frac{2}{p}$ and $\frac{1}{q_3}=\frac{1}{q_1}+\frac{1}{q_2}-\frac{2}{r}$. Assume that ${\omega }_3$ is a continuous, bounded, symmetric weight function. If $m\in W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))\cap L^{\mathrm{\infty }}({\mathbb{R}}^{2n})$, then $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$.

Proof Firstly, we show that $m\in BM[W(p,r,{\omega }_1;p,r,{\omega }_2;\mathrm{\infty },\mathrm{\infty },{\omega }_3)]$. Take any $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. Let $A\times B\subset {\mathbb{R}}^{2n}$ be a closed and bounded rectangle. Since the definition of $W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))$ is independent of the choice of a compact set Q, then, by using Fubini’s theorem, we get

$$\begin{array}{c}{\parallel \hat{f}(\xi )\hat{g}(\eta )\parallel }_{W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))}\hfill \\ ={\parallel F_{\hat{f}\hat{g}}^Q\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}\le C_1{\parallel F_{\hat{f}\hat{g}}^{A\times B}\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}\hfill \\ =C_1{\parallel {\parallel \hat{f}{\chi }_{x+A}\parallel }_{p^{\prime }}{\parallel \hat{g}{\chi }_{y+B}\parallel }_{p^{\prime }}\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}=C_1{\parallel F_{\hat{f}}^A(x)F_{\hat{g}}^B(y)\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}\hfill \\ =C_1{\parallel F_{\hat{f}}^A\parallel }_{r^{\prime }}{\parallel F_{\hat{g}}^B\parallel }_{r^{\prime }}=C_1{\parallel \hat{f}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}{\parallel \hat{g}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}\hfill \end{array}$$

(2.40)

for some $C_1>0$. So, we have $\hat{f}(\xi )\hat{g}(\eta )\in W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))$. By using the Hölder inequality, the Hausdorff-Young inequality and equality (2.40), we obtain

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ \le C_1{\parallel h\parallel }_1{\parallel \hat{f}(\xi )\hat{g}(\eta )\parallel }_{W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}\hfill \\ \le C_1{\parallel h\parallel }_1{\parallel \hat{f}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}{\parallel \hat{g}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}\hfill \\ \le C_1{C}_2{\parallel h\parallel }_{W(L^1,L^1)}{\parallel f\parallel }_{W(L^p,L^r)}{\parallel g\parallel }_{W(L^p,L^r)}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}\hfill \\ \le C_1{C}_2{\parallel {\omega }_3\parallel }_{\mathrm{\infty }}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}{\parallel f\parallel }_{W(L^p,L_{{\omega }_1}^r)}{\parallel g\parallel }_{W(L^p,L_{{\omega }_2}^r)}{\parallel h\parallel }_{W(L^1,L_{{\omega }_3^{-1}}^1)}\hfill \end{array}$$

for some $C_2>0$. Therefore $m\in BM[W(p,r,{\omega }_1;p,r,{\omega }_2;\mathrm{\infty },\mathrm{\infty },{\omega }_3)]$ by Theorem 2.2.

Now, we show that $m\in BM[W(p,r,{\omega }_1;1,1,{\omega }_2;p^{\prime },r^{\prime },{\omega }_3)]$. Again, using Fubini’s theorem, we have

$$\begin{array}{c}{\parallel \hat{f}(-v)\hat{h}(u)\parallel }_{W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))}\hfill \\ \le C_3{\parallel {\parallel \hat{f}(-v)\hat{h}(u){\chi }_{(x,y)+A\times B}\parallel }_{L^{p^{\prime }}({\mathbb{R}}^{2n})}\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}\hfill \\ =C_3{\parallel {\parallel \hat{f}{\chi }_{-x-A}\parallel }_{p^{\prime }}{\parallel \hat{h}{\chi }_{y+B}\parallel }_{p^{\prime }}\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}=C_3{\parallel F_{\hat{f}}^{-A}(-x)F_{\hat{h}}^B(y)\parallel }_{L^{r^{\prime }}({\mathbb{R}}^{2n})}\hfill \\ =C_3{\parallel F_{\hat{f}}^{-A}\parallel }_{r^{\prime }}{\parallel F_{\hat{h}}^B\parallel }_{r^{\prime }}\le C_3{C}_4{\parallel \hat{f}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}{\parallel \hat{h}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}\hfill \end{array}$$

(2.41)

for some $C_3>0$, $C_4>0$. So, $\hat{f}(-v)\hat{h}(u)\in W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))$. Similarly, we have

$$\begin{array}{rcl}{\parallel m(-v,u+v)\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}& \le & C_5{\parallel F_m^{(-A)\times (A+B)}\parallel }_{L^r({\mathbb{R}}^{2n})}\\ \le & C_5{C}_6{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}\end{array}$$

(2.42)

for some $C_5>0$, $C_6>0$. That means $m(-v,u+v)\in W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))$. We set $\xi +\eta =u$ and $\xi =-v$. Then, by using the Hölder inequality, the Hausdorff-Young inequality, (2.41) and (2.42), we get

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ =|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(-v)\hat{g}(u+v)\hat{h}(u)m(-v,u+v)dudv|\hfill \\ \le {\parallel g\parallel }_1{\parallel \hat{f}(-v)\hat{g}(u)\parallel }_{W(L^{p^{\prime }}({\mathbb{R}}^{2n}),L^{r^{\prime }}({\mathbb{R}}^{2n}))}{\parallel m(-v,u+v)\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}\hfill \\ \le C_3{C}_4{C}_5{C}_6{\parallel g\parallel }_1{\parallel \hat{f}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}{\parallel \hat{h}\parallel }_{W(L^{p^{\prime }},L^{r^{\prime }})}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}\hfill \\ \le C_3{C}_4{C}_5{C}_6{C}_7{\parallel {\omega }_3\parallel }_{\mathrm{\infty }}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}{\parallel f\parallel }_{W(L^p,L_{{\omega }_1}^r)}{\parallel g\parallel }_{W(L^1,L_{{\omega }_2}^1)}{\parallel h\parallel }_{W(L^p,L_{{\omega }_3^{-1}}^r)}.\hfill \end{array}$$

Thus, by Theorem 2.2, we obtain $m\in BM[W(p,r,{\omega }_1;1,1,{\omega }_2;p^{\prime },r^{\prime },{\omega }_3)]$. Similarly, if we change the variables $\xi +\eta =u$ and $\eta =-v$, then

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ ={\parallel f\parallel }_1{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\hat{g}(-v)\hat{h}(u)||m(u+v,-v)|dudv\hfill \\ \le C{\parallel {\omega }_3\parallel }_{\mathrm{\infty }}{\parallel m\parallel }_{W(L^p({\mathbb{R}}^{2n}),L^r({\mathbb{R}}^{2n}))}{\parallel f\parallel }_{W(L^1,L_{{\omega }_1}^1)}{\parallel g\parallel }_{W(L^p,L_{{\omega }_2}^r)}{\parallel h\parallel }_{W(L^p,L_{{\omega }_3^{-1}}^r)}.\hfill \end{array}$$

Hence $m\in BM[W(1,1,{\omega }_1;p,r,{\omega }_2;p^{\prime },r^{\prime },{\omega }_3)]$.

We take ${\tilde{p}}_1$, ${\tilde{q}}_1$, ${\tilde{p}}_3$ and ${\tilde{q}}_3$ such that $1\le {\tilde{p}}_1\le p$, $1\le {\tilde{q}}_1\le r$, $p^{\prime }\le {\tilde{p}}_3\le \mathrm{\infty }$ and $r^{\prime }\le {\tilde{q}}_3\le \mathrm{\infty }$. Since $m\in BM[W(p,r,{\omega }_1;p,r,{\omega }_2;\mathrm{\infty },\mathrm{\infty },{\omega }_3)]$ and $m\in BM[W(1,1,{\omega }_1;p,r,{\omega }_2;p^{\prime },r^{\prime },{\omega }_3)]$, we have $m\in BM[W({\tilde{p}}_1,{\tilde{q}}_1,{\omega }_1;p,r,{\omega }_2;{\tilde{p}}_3,{\tilde{q}}_3,{\omega }_3)]$ by the interpolation theorem in [13, 14] such that

$$\frac{1}{{\tilde{p}}_1}=\frac{1-\theta }{p}+\frac{\theta }{1},\frac{1}{{\tilde{p}}_3}=\frac{1-\theta }{\mathrm{\infty }}+\frac{\theta }{p^{\prime }},$$

(2.43)

$$\frac{1}{{\tilde{q}}_1}=\frac{1-\theta }{r}+\frac{\theta }{1},\frac{1}{{\tilde{q}}_3}=\frac{1-\theta }{\mathrm{\infty }}+\frac{\theta }{r^{\prime }}$$

(2.44)

for all $0\le \theta \le 1$. On the other hand, from equalities (2.43) and (2.44), we obtain the equalities $\frac{1}{{\tilde{p}}_1}-\frac{1}{{\tilde{p}}_3}=\frac{1}{p}$ and $\frac{1}{{\tilde{q}}_1}-\frac{1}{{\tilde{q}}_3}=\frac{1}{r}$. Similarly, we take ${\tilde{p}}_2$, ${\tilde{q}}_2$, ${\tilde{r}}_3$ and ${\tilde{s}}_3$ such that $1\le {\tilde{p}}_2\le p$, $1\le {\tilde{q}}_2\le r$, $p^{\prime }\le {\tilde{r}}_3\le \mathrm{\infty }$ and $r^{\prime }\le {\tilde{s}}_3\le \mathrm{\infty }$. Again, if we use $m\in BM[W(p,r,{\omega }_1;p,r,{\omega }_2;\mathrm{\infty },\mathrm{\infty },{\omega }_3)]$ and $m\in BM[W(p,r,{\omega }_1;1,1,{\omega }_2;p^{\prime },r^{\prime },{\omega }_3)]$, we have $m\in BM[W(p,r,{\omega }_1;{\tilde{p}}_2,{\tilde{q}}_2,{\omega }_2;{\tilde{r}}_3,{\tilde{s}}_3,{\omega }_3)]$ by the interpolation theorem in [13, 14] such that

$$\frac{1}{{\tilde{p}}_2}=\frac{1-\theta }{p}+\frac{\theta }{1},\frac{1}{{\tilde{r}}_3}=\frac{1-\theta }{\mathrm{\infty }}+\frac{\theta }{p^{\prime }},$$

(2.45)

$$\frac{1}{{\tilde{q}}_2}=\frac{1-\theta }{r}+\frac{\theta }{1},\frac{1}{{\tilde{s}}_3}=\frac{1-\theta }{\mathrm{\infty }}+\frac{\theta }{r^{\prime }}$$

(2.46)

for all $0\le \theta \le 1$. So, from equalities (2.45) and (2.46), we have $\frac{1}{{\tilde{p}}_2}-\frac{1}{{\tilde{r}}_3}=\frac{1}{p}$ and $\frac{1}{{\tilde{q}}_2}-\frac{1}{{\tilde{s}}_3}=\frac{1}{r}$.

Now, we choose ${\tilde{p}}_1$, ${\tilde{p}}_2$ such that $1\le {\tilde{p}}_1\le p_1<p$ and $1\le {\tilde{p}}_2\le p_2<p$. Let these numbers have the following conditions:

$$\frac{1}{p_1}-\frac{1}{p}=(1-\theta )(\frac{1}{{\tilde{p}}_1}-\frac{1}{p}),$$

(2.47)

$$\frac{1}{p_2}-\frac{1}{p}=(1-\theta )(\frac{1}{{\tilde{p}}_2}-\frac{1}{p})$$

(2.48)

for $0<\theta <1$. Again, we choose ${\tilde{q}}_1$, ${\tilde{q}}_2$ such that $1\le {\tilde{q}}_1\le q_1<r$ and $1\le {\tilde{q}}_2\le q_2<r$. Let these numbers have the following conditions:

$$\frac{1}{q_1}-\frac{1}{r}=(1-\theta )(\frac{1}{{\tilde{q}}_1}-\frac{1}{r}),$$

(2.49)

$$\frac{1}{q_2}-\frac{1}{r}=(1-\theta )(\frac{1}{{\tilde{q}}_2}-\frac{1}{r})$$

(2.50)

for $0<\theta <1$. If we use equalities (2.45), (2.46), (2.47), (2.48), (2.49) and (2.50), we write

$$\frac{1}{p_1}=\frac{1-\theta }{{\tilde{p}}_1}+\frac{\theta }{p},\frac{1}{p_2}=\frac{1-\theta }{p}+\frac{\theta }{{\tilde{p}}_2},$$

(2.51)

$$\frac{1}{q_1}=\frac{1-\theta }{{\tilde{q}}_1}+\frac{\theta }{r},\frac{1}{q_2}=\frac{1-\theta }{r}+\frac{\theta }{{\tilde{q}}_2}.$$

(2.52)

Moreover, using the equalities $\frac{1}{{\tilde{p}}_1}-\frac{1}{{\tilde{p}}_3}=\frac{1}{p}$, $\frac{1}{{\tilde{p}}_2}-\frac{1}{{\tilde{r}}_3}=\frac{1}{p}$, (2.51) and the assumption $\frac{1}{p_3}=\frac{1}{p_1}+\frac{1}{p_2}-\frac{2}{p}$, we obtain

$$\frac{1}{p_3}=\frac{1-\theta }{{\tilde{p}}_3}+\frac{\theta }{{\tilde{r}}_3}.$$

(2.53)

Similarly, using the equalities $\frac{1}{{\tilde{q}}_1}-\frac{1}{{\tilde{q}}_3}=\frac{1}{r}$, $\frac{1}{{\tilde{q}}_2}-\frac{1}{{\tilde{s}}_3}=\frac{1}{r}$, (2.52) and the assumption $\frac{1}{q_3}=\frac{1}{q_1}+\frac{1}{q_2}-\frac{2}{r}$, we obtain

$$\frac{1}{q_3}=\frac{1-\theta }{{\tilde{q}}_3}+\frac{\theta }{{\tilde{s}}_3}.$$

(2.54)

Since $m\in BM[W({\tilde{p}}_1,{\tilde{q}}_1,{\omega }_1;p,r,{\omega }_2;{\tilde{p}}_3,{\tilde{q}}_3,{\omega }_3)]$, $m\in BM[W(p,r,{\omega }_1;{\tilde{p}}_2,{\tilde{q}}_2,{\omega }_2;{\tilde{r}}_3,{\tilde{s}}_3,{\omega }_3)]$, then the bilinear multipliers $B_m:W(L^{{\tilde{p}}_1},L_{{\omega }_1}^{{\tilde{q}}_1})\times W(L^p,L_{{\omega }_2}^r)\to W(L^{{\tilde{p}}_3},L_{{\omega }_3}^{{\tilde{q}}_3})$ and $B_m:W(L^p,L_{{\omega }_1}^r)\times W(L^{{\tilde{p}}_2},L_{{\omega }_2}^{{\tilde{q}}_2})\to W(L^{{\tilde{r}}_3},L_{{\omega }_3}^{{\tilde{s}}_3})$ are bounded. Also, since $1\le {\tilde{p}}_1\le p_1<p$, $1\le {\tilde{q}}_1\le q_1<r$, $1\le {\tilde{q}}_2\le q_2<r$, $1\le {\tilde{p}}_2\le p_2<p$, by equalities (2.53) and (2.54) and by the interpolation theorem in [13], $B_m:W(L^{p_1},L_{{\omega }_1}^{q_1})\times W(L^{p_2},L_{{\omega }_2}^{q_2})\to W(L^{p_3},L_{{\omega }_3}^{q_3})$ is bounded. That means $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$. This completes the proof. □

3 The bilinear multipliers space $BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$

Lemma 3.1 Let $1\le p(x)\le q<\mathrm{\infty }$.

• (a) If ω is a slowly increasing weight function, then $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in the weighted variable exponent Wiener amalgam space $W(L^{p(x)},L_{\omega }^q)$.

• (b) If ω is a continuous, slowly increasing weight function, then $C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ is dense in the weighted variable exponent Wiener amalgam space $W(L^{p(x)},L_{{\omega }^{-1}}^q)$.

This lemma can be proved easily by using the proof technique in Lemma 2.1.

Definition 3.1 Let $p_1(x),p_2(x),p_3(x)\in P({\mathbb{R}}^n)$, $p_1^{\ast }<\mathrm{\infty }$, $p_2^{\ast }<\mathrm{\infty }$, $p_3^{\ast }<\mathrm{\infty }$, $p_1(x)\le q_1$, $p_2(x)\le q_2$, $1\le q_3\le \mathrm{\infty }$ and ${\omega }_1$, ${\omega }_2$, ${\omega }_3$ be weight functions on ${\mathbb{R}}^n$. Assume that ${\omega }_1$, ${\omega }_2$ are slowly increasing functions and $m(\xi ,\eta )$ is a bounded, measurable function on ${\mathbb{R}}^n\times {\mathbb{R}}^n$. Define

$$B_m(f,g)(x)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )m(\xi ,\eta )e^{2\pi i〈\xi +\eta ,x〉}d\xi d\eta$$

for all $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. m is said to be a bilinear multiplier on ${\mathbb{R}}^n$ of type $(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))$ if there exists $C>0$ such that

$${\parallel B_m(f,g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\le C{\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}$$

for all $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. That means $B_m$ extends to a bounded bilinear operator from $W(L^{p_1(x)},L_{{\omega }_1}^{q_1})\times W(L^{p_2(x)},L_{\omega 2}^{q_2})$ to $W(L^{p_3(x)},L_{{\omega }_3}^{q_3})$. We denote by $BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$ the space of all bilinear multipliers of type $(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))$ and

$${\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}=\parallel B_m\parallel .$$

The following theorem can be proved easily by using Lemma 3.1 and the technique of proof of Theorem 2.2.

Theorem 3.1 Let $\frac{1}{p_3(x)}+\frac{1}{p_3^{\prime }(x)}=1$, $\frac{1}{q_3}+\frac{1}{q_3^{\prime }}=1$, $q_3^{\prime }\ge p_3^{\prime }(x)$, $p_3(-x)=p_3(x)$ and ${\omega }_3$ be a continuous, symmetric, slowly increasing weight function. Then $m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$ if and only if there exists $C>0$ such that

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\hfill \\ \le C{\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }(x)},L_{{\omega }_3^{-1}}^{q_3^{\prime }})}\hfill \end{array}$$

for all $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$.

Now we will give some properties of the space $BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$. Since some properties of usual Lebesgue spaces are not true in general in the variable exponent Lebesgue spaces, like translation invariance, then also some properties of the spaces $BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3,q_3,{\omega }_3)]$ do not hold true in general in the spaces $BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$.

Theorem 3.2 If $m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$, then $T_{({\xi }_0,{\eta }_0)}m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$ and

$${\parallel T_{({\xi }_0,{\eta }_0)}m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}={\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}$$

for all $({\xi }_0,{\eta }_0)\in {\mathbb{R}}^{2n}$.

Proof Let $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. Then we have

$${\parallel M_{-{\xi }_0}f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}={\parallel {\parallel e^{2\pi i〈-{\xi }_0,\cdot 〉}f(\cdot ){\chi }_{z+Q}(\cdot )\parallel }_{p_1(x)}\parallel }_{q_1,{\omega }_1}={\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}.$$

Similarly, the equality ${\parallel M_{-{\eta }_0}g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}={\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}$ is written. So, by using these results and the assumption $m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$, we have

$$\begin{array}{c}{\parallel B_{T_{({\xi }_0,{\eta }_0)}m}(f,g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ ={\parallel B_m(M_{-{\xi }_0}f,M_{-{\eta }_0}g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ \le \parallel B_m\parallel {\parallel M_{-{\xi }_0}f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel M_{-{\eta }_0}g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}\hfill \\ =\parallel B_m\parallel {\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}.\hfill \end{array}$$

Thus $T_{({\xi }_0,{\eta }_0)}m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$. Moreover, by using the same technique as in the proof of Theorem 2.4, we obtain

$${\parallel T_{({\xi }_0,{\eta }_0)}m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}={\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}.$$

 □

Theorem 3.3 Let $m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$. Then $\mathrm{\Phi }\ast m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$, and there exists $C>0$ such that

$${\parallel \mathrm{\Phi }\ast m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}\le C{\parallel \mathrm{\Phi }\parallel }_1{\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}$$

for all $\mathrm{\Phi }\in L^1({\mathbb{R}}^{2n})$.

Proof Take any $f,g\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. By Proposition 2.5 in [12], we know that

$$B_{\mathrm{\Phi }\ast m}(f,g)(x)={\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\mathrm{\Phi }(u,v)B_{T_{({\xi }_u,{\eta }_v)}m}(f,g)(x)dudv.$$

(3.1)

Since $m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$, then by Theorem 3.2, $T_{(u,v)}m$ in the space $BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$ and

$${\parallel T_{(u,v)}m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}={\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}.$$

Using (3.1) and the Minkowski inequality in [15], we find $C>0$ such that

$$\begin{array}{c}{\parallel B_{\mathrm{\Phi }\ast m}(f,g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ ={\parallel {\parallel ({\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\mathrm{\Phi }(u,v)B_{T_{(u,v)}m}(f,g)dudv){\chi }_{z+Q}\parallel }_{p_3(x)}\parallel }_{q_3,{\omega }_3}\hfill \\ \le C{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\mathrm{\Phi }(u,v)|{\parallel {\parallel B_{T_{(u,v)}m}(f,g){\chi }_{z+Q}\parallel }_{p_3(x)}\parallel }_{q_3,{\omega }_3}dudv\hfill \\ =C{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\mathrm{\Phi }(u,v)|{\parallel B_{T_{(u,v)}m}(f,g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}dudv\hfill \\ \le C{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}|\mathrm{\Phi }(u,v)|{\parallel T_{(u,v)}m\parallel }_{BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]}\hfill \\ \times {\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}dudv\hfill \\ =C{\parallel m\parallel }_{BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]}\hfill \\ \times {\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}{\parallel \mathrm{\Phi }\parallel }_1.\hfill \end{array}$$

(3.2)

Hence $\mathrm{\Phi }\ast m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$, and by (3.2) we have

$$\begin{array}{c}{\parallel \mathrm{\Phi }\ast m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}\hfill \\ \le C{\parallel \mathrm{\Phi }\parallel }_1{\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}.\hfill \end{array}$$

 □

Theorem 3.4 Let $\frac{1}{p_3(x)}+\frac{1}{p_3^{\prime }(x)}=1$, $\frac{1}{q_3}+\frac{1}{q_3^{\prime }}=1$, $q_3^{\prime }\ge p_3^{\prime }(x)$, $p_3(-x)=p_3(x)$ and ${\omega }_3$ be a continuous, symmetric, slowly increasing weight function. If ${\mathrm{\Psi }}_1\in L_{{\omega }_1}^1({\mathbb{R}}^n)$, ${\mathrm{\Psi }}_2\in L_{{\omega }_2}^1({\mathbb{R}}^n)$ and $m\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$, then ${\hat{\mathrm{\Psi }}}_1(\xi )m(\xi ,\eta ){\hat{\mathrm{\Psi }}}_2(\eta )\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$.

Proof Take any $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$. Then, by Theorem 2.10 in [10], we write the following:

$$|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta )m(\xi ,\eta )d\xi d\eta |\le {\int }_{{\mathbb{R}}^n}|h(y){\tilde{B}}_m(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)(y)|dy.$$

So, by Theorem 11.7.1 in [5] and inequalities (2.37), (2.38), there exists $C>0$ such that

$$\begin{array}{c}|{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}\hat{f}(\xi )\hat{g}(\eta )\hat{h}(\xi +\eta ){\hat{\mathrm{\Psi }}}_1(\xi )m(\xi ,\eta ){\hat{\mathrm{\Psi }}}_2(\eta )d\xi d\eta |\hfill \\ \le {\parallel h\parallel }_{W(L^{p_3^{\prime }(x)},L_{{\omega }^{-1}}^{q_3^{\prime }})}{\parallel {\tilde{B}}_m(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ \le C{\parallel h\parallel }_{W(L^{p_3^{\prime }(x)},L_{{\omega }^{-1}}^{q_3^{\prime }})}{\parallel B_m(f\ast {\mathrm{\Psi }}_1,g\ast {\mathrm{\Psi }}_2)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ \le C{\parallel h\parallel }_{W(L^{p_3^{\prime }(x)},L_{{\omega }^{-1}}^{q_3^{\prime }})}\parallel B_m\parallel {\parallel f\ast {\mathrm{\Psi }}_1\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\ast {\mathrm{\Psi }}_2\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}\hfill \\ \le C\parallel B_m\parallel {\parallel {\mathrm{\Psi }}_1\parallel }_{1,{\omega }_1}{\parallel {\mathrm{\Psi }}_2\parallel }_{1,{\omega }_2}{\parallel f\parallel }_{W(L^{p_1},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2},L_{\omega 2}^{q_2})}{\parallel h\parallel }_{W(L^{p_3^{\prime }(x)},L_{{\omega }^{-1}}^{q_3^{\prime }})}.\hfill \end{array}$$

Hence, ${\hat{\mathrm{\Psi }}}_1(\xi )m(\xi ,\eta ){\hat{\mathrm{\Psi }}}_2(\eta )\in BM[W(p_1,q_1,{\omega }_1;p_2,q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$ by Theorem 3.1. □

Theorem 3.5 Let $m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$. If $Q_1,Q_2\subset {\mathbb{R}}^n$ are bounded sets, then

$$\begin{array}{rcl}h(\xi ,\eta )& =& \frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}m(\xi +u,\eta +v)dudv\\ \in & BM\left[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)\right].\end{array}$$

Proof Let $f,g,h\in C_c^{\mathrm{\infty }}({\mathbb{R}}^n)$ be given. The equality

$$B_h(f,g)(x)=\frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{B}_{T_{(-u,-v)}m}(f,g)(x)dudv$$

is known by Theorem 2.9 in [10]. Using Theorem 3.2, there exists $C>0$ such that

$$\begin{array}{c}{\parallel B_h(f,g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ ={\parallel \frac{1}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{B}_{T_{(-u,-v)}m}(f,g){\chi }_{z+Q}dudv\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}\hfill \\ \le \frac{C}{\mu (Q_1\times Q_2)}{\parallel {\iint }_{Q_1\times Q_2}{\parallel B_{T_{(-u,-v)}m}(f,g){\chi }_{z+Q}\parallel }_{p_3(x)}\parallel }_{q_3,{\omega }_3}dudv\hfill \\ \le \frac{C}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{\parallel {\parallel B_{T_{(-u,-v)}m}(f,g){\chi }_{z+Q}\parallel }_{p_3(x)}\parallel }_{q_3,{\omega }_3}dudv\hfill \\ =\frac{C}{\mu (Q_1\times Q_2)}{\iint }_{Q_1\times Q_2}{\parallel B_{T_{(-u,-v)m}}(f,g)\parallel }_{W(L^{p_3(x)},L_{{\omega }_3}^{q_3})}dudv\hfill \\ \le \frac{1}{\mu (Q_1\times Q_2)}C{\iint }_{Q_1\times Q_2}{\parallel T_{(-u,-v)}m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}\hfill \\ \times {\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}dudv\hfill \\ =C{\parallel m\parallel }_{(W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3))}{\parallel f\parallel }_{W(L^{p_1(x)},L_{{\omega }_1}^{q_1})}{\parallel g\parallel }_{W(L^{p_2(x)},L_{\omega 2}^{q_2})}.\hfill \end{array}$$

Hence $h(\xi ,\eta )\in m\in BM[W(p_1(x),q_1,{\omega }_1;p_2(x),q_2,{\omega }_2;p_3(x),q_3,{\omega }_3)]$. □

Theorem 3.6 Let $r(x)\le s(x)$, $m(x)\le q(x)$, $n(x)\le p(x)$, $s\le r$, $q\le m$, $p\le n$, ${\upsilon }_3\le {\omega }_3$, ${\omega }_2\le {\upsilon }_2$, ${\omega }_1\le {\upsilon }_1$. Then

$$\begin{array}{c}BM\left[W(n(x),n,{\omega }_1;m(x),m,{\omega }_2;s(x),s,{\omega }_3)\right]\hfill \\ \subset BM\left[W(p(x),p,{\upsilon }_1;q(x),q,{\upsilon }_2;r(x),r,{\upsilon }_3)\right].\hfill \end{array}$$

Proof Take any $m\in BM[W(n(x),n,{\omega }_1;m(x),m,{\omega }_2;s(x),s,{\omega }_3)]$. Then there exists $C_1>0$ such that

$${\parallel B_m(f,g)\parallel }_{W(L^{s(x)},L_{{\omega }_3}^s)}\le C_1{\parallel f\parallel }_{W(L^{n(x)},L_{{\omega }_1}^n)}{\parallel g\parallel }_{W(L^{m(x)},L_{\omega 2}^m)}.$$

(3.3)

On the other hand, by Proposition 2.5 in [7] we have $W(L^{s(x)},L_{{\omega }_3}^s)\subset W(L^{r(x)},L_{{\upsilon }_3}^r)$, $W(L^{p(x)},L_{{\upsilon }_1}^p)\subset W(L^{n(x)},L_{{\omega }_1}^n)$ and $W(L^{q(x)},L_{{\upsilon }_2}^q)\subset W(L^{m(x)},L_{\omega 2}^m)$. So, there exist $C_2>0$, $C_3>0$ and $C_4>0$ such that

$${\parallel B_m(f,g)\parallel }_{W(L^{r(x)},L_{{\upsilon }_3}^r)}\le C_2{\parallel B_m(f,g)\parallel }_{W(L^{s(x)},L_{{\omega }_3}^s)},$$

(3.4)

$${\parallel f\parallel }_{W(L^{n(x)},L_{{\omega }_1}^n)}\le C_3{\parallel f\parallel }_{W(L^{p(x)},L_{{\upsilon }_1}^p)}$$

(3.5)

and

$${\parallel g\parallel }_{W(L^{m(x)},L_{\omega 2}^m)}\le C_4{\parallel g\parallel }_{W(L^{q(x)},L_{{\upsilon }_2}^q)}.$$

(3.6)

Combining (3.3), (3.4), (3.5) and (3.6), we get

$${\parallel B_m(f,g)\parallel }_{W(L^{r(x)},L_{{\upsilon }_3}^r)}\le C_1{C}_2{C}_3{C}_4{\parallel f\parallel }_{W(L^{p(x)},L_{{\upsilon }_1}^p)}{\parallel g\parallel }_{W(L^{q(x)},L_{{\upsilon }_2}^q)}.$$

That means $m\in BM[W(p(x),p,{\upsilon }_1;q(x),q,{\upsilon }_2;r(x),r,{\upsilon }_3)]$. Hence, we obtain $BM[W(n(x),n,{\omega }_1;m(x),m,{\omega }_2;s(x),s,{\omega }_3)]\subset BM[W(p(x),p,{\upsilon }_1;q(x),q,{\upsilon }_2;r(x),r,{\upsilon }_3)]$. □