Abstract
In this paper, a class of refinable functions is given by smoothening pseudo-splines in order to get divergence free and curl free wavelets. The regularity and stability of them are discussed. Based on that, the corresponding Riesz wavelets are constructed.
Similar content being viewed by others
1 Introduction
We denote by ℤ and ℝ the set of integers and real numbers, respectively. Let stand for the classical Lebesgue space
with the norm and consisting of all Lebesgue measurable and bounded functions on ℝ. Similarly, the discrete space with . As usual, given , its Fourier transform is defined by
on ℝ. The Fourier transform of a function in is understood as the unitary extension. We write for the convolution , defined for any pair of functions f and g such that the integral exists almost everywhere. Clearly, in the frequency domain, when all the Fourier transforms exist in that formula. Given , is called a Riesz basis of its linearly generating space, if for each there exist two positive constants A and B such that
The numbers A, B are called lower Riesz bound and upper Riesz bound, respectively.
Multiresolution analysis provides a classical method to construct wavelets.
Definition 1 A multiresolution analysis of means a sequence of closed linear subspaces of which satisfies
-
(i)
, ,
-
(ii)
if and only if ,
-
(iii)
and ,
-
(iv)
there exists a function such that forms a Riesz basis of .
The function ϕ in Definition 1 is said to be a scaling function, if it satisfies
for some sequence . Define the Fourier series of a sequence by
Then the refinement equation (1.2) becomes
The function is called the refinement mask of ϕ. The pseudo-spline of Type I was first introduced in [1] to construct tight framelets. The pseudo-spline of Type II was first studied by Dong and Shen in [2]. There have been many developments in the theory of pseudo-splines over the past ten years [3, 4]. Its applications in image denoising and image in-painting are also very extensive [5, 6]. The pseudo-spline is defined by its refinement mask. The refinement mask of a pseudo-spline of Type I with order is given by
and the refinement of a pseudo-spline of Type II with order is given by
The mask of Type I is obtained by taking the square root of the mask of Type II using the Fejér-Riesz lemma [7], i.e. . The corresponding pseudo-spline can be defined in terms of their Fourier transform, i.e.
In order to smoothen the pseudo-spline, one can use the convolution method. Take the smoothed pseudo-spline

where denotes the characteristic function of interval and . This is equivalent to
Thus the symbol of becomes
Therefore, we define the smoothed pseudo-spline by its refinement mask for Type I:
and for Type II:
where . When , it is the pseudo-spline. When , it can be considered as an extension of pseudo-spline. Define the translated form of the Type II by
Then we get the differential relation
This inherits the property of a B-spline.
Remark 1 One may think that smoothing the pseudo-splines by convolving them with B-splines seems unnecessary since one can simply increase m of the original pseudo-splines. However, by increasing m, we cannot get the differential relation (1.6), which is important for the construction of divergence free wavelets and curl free wavelets in the analysis of incompressible turbulent flows [8, 9].
Remark 2 Similar to the definition of (1.5), we can define a smoothed dual pseudo-spline by its refinement mask,
as an extension of dual pseudo-splines in [3] and get the corresponding wavelets.
Remark 3 In addition, one can assume in (1.5) and (1.7), as a generalization of fractional splines in [10].
2 Some lemmas
This section gives some lemmas that will be used to prove several results of this paper. We start with some results from [2].
Lemma 1 [2]
For given nonnegative integers m, j, ℓ,
This lemma will be used in Section 4 in order to prove the Riesz basis property of wavelets. Define , and where , r, m, ℓ are nonnegative integers and . Then one can find that
and the following lemma holds.
Lemma 2 [2]
For nonnegative integers m and ℓ with , let and be the polynomials defined above. Then
-
(1)
;
-
(2)
.
With the two lemmas in hand, the basic property of the polynomial , which will be used in Section 4, is given.
Lemma 3 For nonnegative integers r, m and ℓ,
-
(1)
define ; then
-
(2)
define ; then
Proof Since , its derivative is
So the derivative is , where
and
Now, we compute them, respectively. For I, by using (1) of Lemma 2, one has
For II, by using (2) of Lemma 2, one has
For , since for all and for all , one has
This means reaches its minimum value at the point . Furthermore,
This completes the proof of (1). For (2) of this lemma, since
we have , where
and
For III, by (1) of Lemma 2, we have
For IV, by (2) of Lemma 2, we have
Since
and for every j,
we have
This means reaches its minimum at point . Furthermore, we have
This completes the lemma. □
3 Regularity and stability of scaling function
In this section, we discuss the regularity and stability of a scaling function generated by the refinement mask of a smoothed pseudo-spline. Let
Then the decay of can be characterized by as stated in the following theorem.
Theorem 1 [2]
Let be a refinement mask of the refinable function ϕ of the form
Suppose that
Then , with , and this decay is optimal.
In order to use this lemma, one needs to consider the polynomial corresponding to . In fact, Dong and Shen give an important proposition to estimate it in the following proposition.
Proposition 1 [2]
Let be defined as in Section 2, where m, ℓ are nonnegative integers with . Then
Combing Theorem 1 and Proposition 1, we have the following theorem, which characterizes the regularity of a smoothed pseudo-spline.
Theorem 2 Let 2ϕ be the smoothed pseudo-spline of Type II with order r, m, ℓ, then
where . Consequently, where . Furthermore, let 1ϕ be the smoothed pseudo-spline of Type I with order n, m, ℓ. Then
Consequently, with .
Proof Notice that in Theorem 1 is exactly and ; one can easily prove this theorem by Theorem 1 and Proposition 1. □
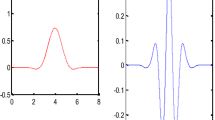
This theorem shows for . Since , the regularity of ϕ is better than a pseudo-spline but the support is longer. For , , the smoothed pseudo-spline is shown in Figure 1.
Now, we consider the stability of the smoothed pseudo-spline. When ϕ is compactly supported in , it was shown by Jia and Micchelli [11] that the upper Riesz bound in (1.1) always exists. Furthermore, they assert that the existence of a lower Riesz bound is equivalent to
where 0 denotes the zero sequence in . Since a smoothed pseudo-spline is compactly supported and belongs to for , the stability is equivalent to (3.1).
Theorem 3 Smoothed pseudo-splines are stable.
Proof By the definition of refinement mask, for each fixed and for any , holds for all . Therefore, we have
where stands for the B-spline with order r. Since is stable, the vector . Hence .
For a smoothed pseudo-spline of Type I, since , one has
Therefore, the set of zeros of is contained in that of and this guarantees the stability of . □
This theorem shows the stability of a smoothed pseudo-spline. From the definition of a Riesz basis, one can find that the translate of a smoothed pseudo-spline is also linearly independent.
4 Riesz wavelets
Since all smoothed pseudo-splines are compactly supported, refinable, stable in , the sequence of spaces defined via Definition 1 forms an MRA. The corresponding wavelets can be constructed by the classical method. Define
and . Then is a Riesz basis. To prove this, the following theorem is needed.
Theorem 4 [2]
Let be a finitely supported refinement mask of a refinable function with and , such that can be factorized into the form
where ℒ is the Fourier series of a finitely supported sequence with . Suppose that
Define and . Assume that and . Then is a Riesz basis for .
From the above theorem, the key step is to estimate the upper Riesz bound of and . Notice that
One has , and
Thus, we have the following theorem.
Theorem 5 Let k ϕ, be the smoothed pseudo-spline of Types I and II with order . The refinement masks k a are given in (1.3) and (1.4). Define
Then forms a Riesz basis for .
Proof By (1) of Lemma 3, one obtains
Applying Lemma 1, one obtains . Similarly, one can get
Notice that
Hence, for . By using Theorem 4, one gets the desired result. □
By definition, the wavelets are also in and have the same regularity as the scaling function. Still, the support is longer than for pseudo-spline wavelets. For , , , the smoothed pseudo-spline is shown in Figure 2.
References
Daubechies I, Han B, Ron A, Shen Z: Framelets: MRA-based constructions of wavelet frames. Appl. Comput. Harmon. Anal. 2003,14(1):1-46. 10.1016/S1063-5203(02)00511-0
Dong B, Shen Z: Pseudo-splines, wavelets and framelets. Appl. Comput. Harmon. Anal. 2007,22(1):78-104. 10.1016/j.acha.2006.04.008
Dong B, Dyn N, Hormann K: Properties of dual pseudo-splines. Appl. Comput. Harmon. Anal. 2010,29(1):104-110. 10.1016/j.acha.2009.08.010
Shen Y, Li S, Mo Q: Complex wavelets and framelets from pseudo splines. J. Fourier Anal. Appl. 2010,16(6):885-900. 10.1007/s00041-009-9095-8
Cai J-F, Shen Z: Framelet based deconvolution. J. Comput. Math. 2010,28(3):289-308.
Cai J, Chan R, Shen L, Shen Z: Tight frame based method for high-resolution image reconstruction. Ser. Contemp. Appl. Math. CAM 14. In Wavelet Methods in Mathematical Analysis and Engineering. Higher Ed. Press, Beijing; 2010:1-36.
Daubechies I CBMS-NSF Regional Conference Series in Applied Mathematics 61. In Ten Lectures on Wavelets. SIAM, Philadelphia; 1992.
Deriaz E, Perrier V: Direct numerical simulation of turbulence using divergence-free wavelets. Multiscale Model. Simul. 2008,7(3):1101-1129.
Chuang Z-T, Liu Y: Wavelets with differential relation. Acta Math. Sin. Engl. Ser. 2011,27(5):1011-1022.
Unser M, Blu T: Fractional splines and wavelets. SIAM Rev. 2000 (electronic),42(1):43-67. (electronic) 10.1137/S0036144598349435
Jia RQ, Micchelli CA: Using the refinement equations for the construction of pre-wavelets. II. Powers of two. In Curves and Surfaces. Academic Press, Boston; 1991: (Chamonix-Mont-Blanc, 1990)209-246. (Chamonix-Mont-Blanc, 1990)
Acknowledgements
This study was partially supported by the Joint Funds of the National Natural Science Foundation of China (Grant No. U1204103). The authors would like to express their thanks to the reviewers for their helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed to each part of this work equally and read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhuang, Z., Yang, J. A class of generalized pseudo-splines. J Inequal Appl 2014, 359 (2014). https://doi.org/10.1186/1029-242X-2014-359
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2014-359