Abstract
For , the sum of the two largest Laplacian eigenvalues of a tree T, an upper bound is obtained. Moreover, among all trees with vertices, the unique tree which attains the maximal value of is determined.
MSC:05C50.
Similar content being viewed by others
1 Introduction
Let be the vertex set and be the edge set of a graph G. The numbers of vertices and edges of G are denoted by and , respectively. For a vertex , let be the set of vertices adjacent to v and be the degree of v. Particularly, denote by the maximum degree of G. The diameter of a connected graph G, denoted by , is the maximum distance among all pairs of vertices in G. Let be the adjacency matrix of G and be the diagonal matrix of vertex degrees. The matrix is called the Laplacian matrix of G and its eigenvalues are called the Laplacian eigenvalues of G. Let be the Laplacian eigenvalues of a graph G with n vertices. It is well known that and . In particular, is called the algebraic connectivity of G and it is denoted by .
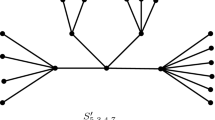
The Laplacian matrix is an important topic in the theory of graph spectra. Particularly, much literature has paid attention to , , or for trees (see, for example, [1–6]). Let be the star of order n, be the tree obtained from two stars , by joining a path of length k between their central vertices (see Figure 1). As is well known, among all trees of order n, has the largest value of (see [7]) and has the second largest value of (see [6]). On the other hand, Guo [4] proved that these two trees also attain the first two smallest values of , respectively. This implies that , cannot attain simultaneously the maximal (or minimal) value and even the relation between them seems like a seesaw. Therefore, it is interesting to investigate the value of . Moreover, Zhang [6] showed that the , , attain simultaneously the largest value of among all trees with 2k vertices. Then Shao et al.[5] showed that attains the largest value of among all trees with vertices.
Another motivation to study the value of came from a result of Haemers et al.[8], who showed that for any graph G. This result implies that Brouwer’s conjecture [9],
is true for . Considering a tree T, we have . Recently, Fritscher et al.[10] improved this bound by giving . This paper determines the extremal tree that attains the bound of . Moreover, for general connected graphs, we also give a conjecture on the extremal graphs for .
2 A sharp upper bound of
Let be the sum of the largest k Laplacian eigenvalues of a graph G. When , we shall write instead of for simplicity. For graphs G and H, we denote by the graph with vertex set and edge set . The following lemmas come from an important result as regards a real symmetric matrix.
Lemma 2.1 ([8])
Letbe some edge-disjoint graphs. Thenfor any k.
Lemma 2.2 ([8])
For any graph G, .
Lemma 2.3 Let G be a connected graph, and. Then
-
(i)
[11], with equality if and only if.
-
(ii)
[7], with equality if and only if the complement of G is disconnected.
-
(iii)
[12].
Lemma 2.4 ([6])
Let T be a tree of order n. If, then, with equality if and only if.
Corollary 2.5 Let T be a tree with n vertices and diameter. Then.
Proof Note that any tree T has diameter if . According to Lemma 2.4, . Further, by Lemma 2.3,
for . For , a straightforward calculation shows that . □
Lemma 2.6 ([2])
Let T be a tree of order n and diameter. Then, with equality if and only if.
Lemma 2.7 ([11])
Let G be a graph with a vertex u of degree one. Then.
Lemma 2.7 implies that the algebraic connectivity of a tree is not greater than that of its subtree.
Lemma 2.8 ([4])
Let () be a tree obtained from a starby replacing its k edges with k paths of length two, respectively. If, then.
The following lemma can be found in [13] and is known as the Interlacing Theorem of Laplacian eigenvalues.
Lemma 2.9 Let G be a graph of order n and H be a graph obtained from G by deleting an edge. Then
Next we give the main theorem of this section. Its proof is divided into several sequent claims.
Theorem 2.10 For any tree T with order, . The equality holds if and only if.
Claim 2.11 For any tree T with orderand diameter, except that.
Proof If , then for some positive integers a, b with . It is well known that the Laplacian characteristic polynomial of is , where
Note that contains as a subtree. By Lemma 2.9, . Moreover, we know that for any tree T, , with equality if and only if T is a star. These imply that , , and consist of the three roots of . As follows from (1), we have
By virtue of Lemma 2.6, we have except that . Equivalently, except that .
If , then . We first give a lower bound of for :
Indeed, by (2) it suffices to show . Note that for , contains as a subtree. By Lemma 2.7, .
Note that for . According to (3), we have for . As for , a straightforward calculation shows that
Also we have . □
Claim 2.12 For any tree T with order n and diameter, .
Proof Since , then and there is a path of length 5 in T. By inequality (3), it suffices to show . First suppose that there is a path in T such that either or . Let , be the two components of . Clearly, both and have at least two edges.
If , of attain at the same component, say , then by Lemma 2.2,
Note that . By Lemma 2.1,
Otherwise, . Whether or , we can observe that . Say , then by Corollary 2.5, . By Lemma 2.3(ii), . Hence,
Next, we may assume that each path of length 5 in T has and . This implies that and for some integers a, b with . If , then T is isomorphic to a path of order 6 and a straightforward calculation shows that , as claimed. Otherwise, assume without loss of generality that . Then . Let , be the two components of with . Then both and have at least two edges. If , of attain at the same component, say , then by Lemmas 2.1 and 2.2,
Otherwise, . Note that . Since , by Corollary 2.5, . So
□
Claim 2.13 For any tree T with order n and diameter 4, .
Proof First suppose that T contains a path such that . Now and it suffices to show . Without loss of generality assume that . Let , be the two components of with . Then both and have at least two edges.
If , of attain at the same component, say , then similarly to inequalities (5) and (6), we can observe that .
Now let . If , then and hence . So
If , then for some positive integers a, b with . Moreover, since , then . If , a straightforward calculations show that . Otherwise, contains either or as a subtree. Since
it follows from Lemma 2.9 that . Since is not a star, . On the other hand, note that the matrix has a identical rows and b different identical rows, so the multiplicity of eigenvalue 1 is at least and else five eigenvalues are , , , and . Since , we have
This implies that .
Next, it suffices to consider the case that each path of T has . This implies that for some and , since . According to Lemma 2.8, . Moreover, by Lemma 2.3,
Thus for ,
When , is a path. Comparing with (4), . This completes the proof. □
Following from Claims 2.11-2.13, Theorem 2.10 holds and the unique tree with maximal is . According to (2),
Theorem 2.14 Let m, n be two positive integers withandbe a graph of order n and size m obtained from a given edge uv by joiningindependent vertices with u and v, respectively, and anotherindependent vertices with u. Then.
Proof Let be a graph obtained by joining a vertex to s vertices of a given complete graph of order and be its complement graph. Then is isomorphic to the union of and s isolated vertices. Clearly, the Laplacian eigenvalues of consist of , 1 with multiplicity and 0 with multiplicity . Recall that for any graph G with n vertices, for and . So the Laplacian eigenvalues of consist of with multiplicity s, with multiplicity , s and 0.
Now is isomorphic to the union of and an isolated vertex. So the Laplacian eigenvalues of consist of with multiplicity , with multiplicity , , and 0 with multiplicity 2. Therefore, the Laplacian eigenvalues of consist of n, , 2 with multiplicity , 1 with multiplicity and 0. So . □
Recall that for any graph G. When , Haemers’ bound is clearly not attainable. Theorem 2.14 implies that if , Haemers’ bound is always sharp for connected graphs other than trees. Ending the paper, we present a conjecture on the uniqueness of the extremal graph.
Conjecture 2.15 Among all connected graphs with n vertices andedges, is the unique graph with maximal value of.
References
Bıyıkoǧlu T, Leydold J: Algebraic connectivity and degree sequences of trees. Linear Algebra Appl. 2009, 430: 811–817. 10.1016/j.laa.2008.09.030
Fallat S, Kirkland S: Extremizing algebraic connectivity subject to graph theoretic constraints. Electron. J. Linear Algebra 1998, 3: 48–74.
Fan YZ, Xu J, Wang Y, Liang D: The Laplacian spread of a tree. Discrete Math. Theor. Comput. Sci. 2008,10(1):79–86.
Guo JM: On the second largest Laplacian eigenvalue of trees. Linear Algebra Appl. 2005, 404: 251–261.
Shao JY, Zhang L, Yuan XY: On the second Laplacian eigenvalues of trees of odd order. Linear Algebra Appl. 2006, 419: 475–485. 10.1016/j.laa.2006.05.021
Zhang XD, Li JS: The two largest eigenvalues of Laplacian matrices of trees. J. Univ. Sci. Technol. China 1998, 28: 513–518.
Anderson WN, Morley TD: Eigenvalues of the Laplacian of a graph. Linear Multilinear Algebra 1985, 18: 141–145. 10.1080/03081088508817681
Haemers WH, Mohammadian A, Tayfeh-Rezaie B: On the sum of Laplacian eigenvalues of graphs. Linear Algebra Appl. 2010, 432: 2214–2221. 10.1016/j.laa.2009.03.038
Brouwer AE, Haemers WH: Spectra of Graphs. Springer, New York; 2012.
Fritscher E, Hoppen C, Rocha I, Trevisan V: On the sum of the Laplacian eigenvalues of a tree. Linear Algebra Appl. 2011, 435: 371–399. 10.1016/j.laa.2011.01.036
Grone R, Merris R, Sunder VS: The Laplacian spectrum of a graph II. SIAM J. Matrix Anal. Appl. 1990, 11: 218–238. 10.1137/0611016
Merris R: A note on the Laplacian graph eigenvalues. Linear Algebra Appl. 1998, 285: 33–35. 10.1016/S0024-3795(98)10148-9
Godsil C, Royle G: Algebraic Graph Theory. Springer, New York; 2001.
Acknowledgements
The authors are grateful to the referees for carefully reading the manuscript and for providing some comments and suggestions, which led to improvements in the paper. The research was supported by the National Natural Science Foundation of China (11101057, 11201432), the Foundation for Young Talents in College of Anhui Province (2012SQRL170) and the Natural Science Foundation of Anhui Province (1308085MA03).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
MG carried out the proofs of the main results in the manuscript. MQZ and YFW participated in the design of the study and drafted the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Guan, M., Zhai, M. & Wu, Y. On the sum of the two largest Laplacian eigenvalues of trees. J Inequal Appl 2014, 242 (2014). https://doi.org/10.1186/1029-242X-2014-242
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2014-242