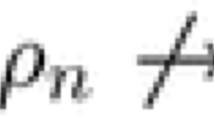Some normality criteria for families of meromorphic functions

Abstract

In the note, we study the normality of families of meromorphic functions. We consider whether a family of meromorphic functions ℱ is normal in D if, for a normal family $\mathcal{G}$ and for each function $f\in \mathcal{F}$, there exists $g\in \mathcal{G}$ such that $f^n{f}^{\prime }=a_i$ implies $g^n{g}^{\prime }=a_i$ for two distinct nonzero points $a_i$, $i=1,2$ and an integer n. An example shows that the condition in our results is best possible.

MSC:30D45, 30D35.

1 Introduction and main results

Let $f(z)$ and $g(z)$ be two nonconstant meromorphic functions in a domain $D\subseteq \mathbb{C}$, and let a be a finite complex value. We say that f and g share a CM (or IM) in D provided that $f-a$ and $g-a$ have the same zeros counting (or ignoring) multiplicity in D. If $g=a$ whenever $f=a$, we denote it by $f=a⟹g=a$. When $a=\mathrm{\infty }$, the zeros of $f-a$ means the poles of f (see [1]). It is assumed that the reader is familiar with the standard notations and the basic results of Nevanlinna’s value-distribution theory (see [2–4] or [1]).

Bloch’s principle [5] states that every condition which reduces a meromorphic function in the plane ℂ to be a constant forces a family of meromorphic functions in a domain D to be normal. Although the principle is false in general (see [6]), many authors proved normality criterion for families of meromorphic functions corresponding to a Liouville-Picard type theorem (see [4]).

It is also more interesting to find normality criteria from the point of view of shared values. In this area, Schwick [7] first proved an interesting result which states that a family of meromorphic functions in a domain is normal if every function shares three distinct finite complex numbers with its first derivative therein. Later, more results about normality criteria concerning shared values have emerged; for instance, see [8–10]. In recent years, this subject has attracted the attention of many researchers worldwide. Studying normal families of functions is of considerable interest. For example, they are used in operator theory on spaces of analytic functions (see, for example, [11], [[12], Lemma 2.5], [[13], Lemma 2.2]).

We now first introduce a normality criterion related to a Hayman normal conjecture [14].

Theorem 1.1 Let ℱ be a family of meromorphic functions on D and $n\in \mathbb{N}$. If each function $f(z)$ of family ℱ satisfies $f^n(z)f^{\prime }(z)\ne 1$, then ℱ is normal in D.

The proof of Theorem 1.1 is due to Gu [15] for $n\ge 3$, Pang [16] for $n=2$, Chen and Fang [17] for $n=1$. In 2004, by the ideas of shared values, Fang and Zalcman [18] obtained the following.

Theorem 1.2 Let ℱ be a family of meromorphic functions on D and $n\in \mathbb{N}$. If for each pair of functions f and g in ℱ, f and g share the value 0 and $f^n{f}^{\prime }$ and $g^n{g}^{\prime }$ share a nonzero value a in D, then ℱ is normal in D.

In 2008, Zhang [10] obtained some criteria for normality of ℱ in terms of the multiplicities of the zeros and poles of the functions in ℱ and used them to improve Theorem 1.2 as follows.

Theorem 1.3 Let ℱ be a family of meromorphic functions in D satisfying that all of zeros and poles of $f\in \mathcal{F}$ have multiplicities at least 3. If for each pair of functions f and g in ℱ, $f^{\prime }$ and $g^{\prime }$ share a nonzero value a in D, then ℱ is normal in D.

Theorem 1.4 Let ℱ be a family of meromorphic functions on D and $n\in \mathbb{N}$. If $n\ge 2$ and for each pair of functions f and g in ℱ, $f^n{f}^{\prime }$ and $g^n{g}^{\prime }$ share a nonzero value a in D, then ℱ is normal in D.

Zhang [10] gave the following example to show that Theorem 1.4 is not true when $n=1$, and therefore the condition $n\ge 2$ is best possible.

Example 1.1 The family of holomorphic functions $\mathcal{F}=\{f_j(z)=\sqrt{j}(z+\frac{1}{j}):j=1,2,\dots \}$ is not normal in $D=\{z:|z|<1\}$. This is deduced by $f_j^{\mathrm{\#}}(0)=\frac{j\sqrt{j}}{j+1}\to \mathrm{\infty }$ as $j\to \mathrm{\infty }$ and Marty’s criterion [2], although for any $f_j(z)\in \mathcal{F}$, $f_j{f}_j^{\prime }=jz+1$. So, for each pair m, j, $f_m{f}_m^{\prime }$ and $f_j{f}_j^{\prime }$ share the value 1.

Here $f^{\mathrm{\#}}(\xi )$ denotes the spherical derivative

$$f^{\mathrm{\#}}(\xi )=\frac{|f^{\prime }(\xi )|}{1+{|f(\xi )|}^2}.$$

Recently, Yuan et al. [19] improved Theorem 1.3 and used it to consider Theorem 1.4 when $n=1$. They proved the following theorems.

Theorem 1.5 Let ℱ be a family of meromorphic functions on D such that all of zeroes of each $f\in \mathcal{F}$ have multiplicities at least 4 and all of poles of $f\in \mathcal{F}$ are multiple. If for each pair of functions f and g in ℱ, $f^{\prime }$ and $g^{\prime }$ share a nonzero value a in D, then ℱ is normal in D.

Theorem 1.6 Let ℱ be a family of meromorphic functions on D such that all of zeroes of each $f\in \mathcal{F}$ are multiple. If for each pair of functions f and g in ℱ, $f{f}^{\prime }$ and $g{g}^{\prime }$ share a nonzero value a in D, then ℱ is normal in D.

Remark 1.7 Example 1.1 shows that the condition that all of zeros of $f\in \mathcal{F}$ are multiple in Theorem 1.6 is best possible.

In this paper, we will consider the related problems concerning two families. Our main results are as follows.

Theorem 1.8 Let ℱ and $\mathcal{G}$ be two families of meromorphic functions in $D\subseteq \mathbb{C}$, k be a positive integer and $a_i$ ($i=1,2$) be two distinct nonzero constants. Suppose that for each function $f\in \mathcal{F}$, all its zeros are of multiplicity at least $k+1$ and all its poles are multiple.

If $\mathcal{G}$ is normal and for each function $f\in \mathcal{F}$, there exists $g\in \mathcal{G}$ such that $f^{(k)}=a_i⟹g^{(k)}=a_i$ for $i=1,2$, then ℱ is normal in D.

Theorem 1.9 Let ℱ and $\mathcal{G}$ be two families of meromorphic functions on D and $a_i$ ($i=1,2$) be two distinct nonzero constants. If all of zeroes of $f\in \mathcal{F}$ have multiplicities at least 3, $\mathcal{G}$ is normal and for each function $f\in \mathcal{F}$, there exists $g\in \mathcal{G}$ such that $f^{\prime }=a_i⟹g^{\prime }=a_i$ for $i=1,2$, then ℱ is normal in D.

Example 1.2 The family of meromorphic functions $\mathcal{F}=\{f_j(z)=\frac{1}{jz}:j=1,2,\dots \}$ is not normal in $D=\{z:|z|<1\}$. This is deduced by $f_j^{\mathrm{\#}}(0)=j\to \mathrm{\infty }$ as $j\to \mathrm{\infty }$ and Marty’s criterion [2]. The family of holomorphic functions $\mathcal{G}=\{g_j(z):j=1,2,\dots \}$ is normal in D, where

$$g_j(z)=\frac{z^{2k+1}}{(2k+1)(2k)\cdots (k+2)}+(1-\frac{{(-1)}^{k}k!}{j})\frac{z^k}{k!}+3.$$

However, for any $f_j(z)\in \mathcal{F}$ and $g_j(z)\in \mathcal{G}$, $f_j(z)\ne 0$ and $g_j(z)\ne 0$ and $f_j^{(k)}(z)=1$ if and only if $g_j^{(k)}(z)=1$ in D.

Noting that normality of families of ℱ and ${\mathcal{F}}^{\ast }=\{\frac{1}{f}|f\in \mathcal{F}\}$ is the same by famous Marty’s criterion, we obtain the following criteria.

Theorem 1.10 Let ℱ and $\mathcal{G}$ be two families of meromorphic functions on D and $a_i$ ($i=1,2$) be two distinct nonzero constants. Suppose that n ($n\ne 0$, −1 and −2) is an integer number. If $\mathcal{G}$ is normal and for each function $f\in \mathcal{F}$, there exists $g\in \mathcal{G}$ such that $f^n{f}^{\prime }=a_i⟹g^n{g}^{\prime }=a_i$ for $i=1,2$, then ℱ is normal in D.

Theorem 1.11 Let ℱ and $\mathcal{G}$ be two families of meromorphic functions on D and $a_i$ ($i=1,2$) be two distinct nonzero constants. If all of poles of $f\in \mathcal{F}$ have multiplicities at least 3, $\mathcal{G}$ is normal and for each function $f\in \mathcal{F}$, there exists $g\in \mathcal{G}$ such that $f^{-2}{f}^{\prime }=a_i⟹g^{-2}{g}^{\prime }=a_i$ for $i=1,2$, then ℱ is normal in D.

Remark 1.12 Example 1.2 shows that the condition in Theorem 1.8 and Theorem 1.9 that for each $f\in \mathcal{F}$, there exists $g\in \mathcal{G}$ such that $f^{(k)}=a_i⟹g^{(k)}=a_i$ for $a_i\ne 0$, $i=1,2$, is best possible.

2 Preliminary lemmas

In order to prove our result, we need the following lemmas. The first one is an extension of a result by Zalcman in [20] concerning normal families.

Lemma 2.1 [21]

Let ℱ be a family of meromorphic functions on the unit disc such that all zeros of functions in ℱ have multiplicity greater than p and all poles of functions in ℱ have multiplicity greater than q. Let α be a real number satisfying $-q<\alpha <p$. Then ℱ is not normal at 0 if and only if there exist

• (a) a number $0<r<1$;

• (b) points $z_n$ with $|z_n|<r$;

• (c) functions $f_n\in \mathcal{F}$;

• (d) positive numbers ${\rho }_n\to 0$

such that $g_n(\zeta ):={\rho }^{-\alpha }{f}_n(z_n+{\rho }_n\zeta )$ converges spherically uniformly on each compact subset of ℂ to a non-constant meromorphic function $g(\zeta )$, its all zeros are of multiplicity greater than p and its all poles are of multiplicity greater than q and its order is at most 2.

Remark 2.2 If ℱ is a family of holomorphic functions on the unit disc in Lemma 2.1, then $g(\zeta )$ is a nonconstant entire function whose order is at most 1.

The order of g is defined by using the Nevanlinna’s characteristic function $T(r,g)$:

$$\rho (g)=\underset{r\to \mathrm{\infty }}{lim}sup\frac{logT(r,g)}{logr}.$$

Lemma 2.3 ([22] or [23])

Let $f(z)$ be a meromorphic function of finite order in the plane, k be a positive integer and $a\in \mathbb{C}\mathrm{\setminus }\{0\}$. Suppose that all its zeros are of multiplicity at least $k+1$ and all its poles are multiple. If $f^{(k)}(z)\ne a$, then $f(z)$ is constant.

Lemma 2.4 [24]

Let f be a meromorphic function of finite order in the plane and $a\in \mathbb{C}\mathrm{\setminus }\{0\}$. If all its zeros are of multiplicity at least 3 and $f^{\prime }(z)\ne a$, then $f(z)$ is a constant.

3 Proofs of the results

Proof of Theorem 1.8 Suppose that ℱ is not normal in D. Then there exists at least one point $z_0$ such that ℱ is not normal at the point $z_0$. Without loss of generality, we assume that $z_0=0$. By Lemma 2.1, there exist points $z_j\to 0$, positive numbers ${\rho }_j\to 0$ and functions $f_j\in \mathcal{F}$ such that

$$F_j(\xi )={\rho }_j^{-k}{f}_j(z_j+{\rho }_j\xi )\Rightarrow F(\xi ),$$

(3.1)

locally uniformly with respect to the spherical metric, where F is a non-constant meromorphic function in ℂ satisfying all of whose zeros are of multiplicity at least $k+1$ and all of whose poles are multiple. Moreover, the order of F is less than two.

From (3.1) we know

$$F_j^{(k)}(\xi )=f_j^{(k)}(z_j+{\rho }_j\xi )\Rightarrow F^{(k)}(\xi )$$

(3.2)

also locally uniformly with respect to the spherical metric.

Combining with Lemma 2.3, we know that $F^{(k)}(\xi )$ takes two distinct nonzero finite values $\{a_1,a_2\}$. Set ${\xi }_0$ and ${\xi }_0^{\ast }$ to be two zeros of $F^{(k)}-a_1$ and $F^{(k)}-a_2$, respectively. Obviously, ${\xi }_0\ne {\xi }_0^{\ast }$, and then choose δ (>0) small enough such that $D({\xi }_0,\delta )\cap D({\xi }_0^{\ast },\delta )=\varphi$, where $D({\xi }_0,\delta )=\{\xi :|\xi -{\xi }_0|<\delta \}$ and $D({\xi }_0^{\ast },\delta )=\{\xi :|\xi -{\xi }_0^{\ast }|<\delta \}$. From (3.2), by Hurwitz’s theorem, there exist points ${\xi }_j\in D({\xi }_0,\delta )$, ${\xi }_j^{\ast }\in D({\xi }_0^{\ast },\delta )$ such that for sufficiently large j,

$$f_j^{(k)}(z_j+{\rho }_j{\xi }_j)-a_1=0,f_j^{(k)}(z_j+{\rho }_j{\xi }_j^{\ast })-a_2=0.$$

(3.3)

It follows from (3.3) and the hypothesis of Theorem 1.8 that

$$g_j^{(k)}(z_j+{\rho }_j{\xi }_j)=a_1,g_j^{(k)}(z_j+{\rho }_j{\xi }_j^{\ast })=a_2.$$

(3.4)

Since $\mathcal{G}$ is normal, without loss of generality, we assume that

$$g_j(z)\to g(z),$$

(3.5)

locally uniformly with respect to the spherical metric.

By (3.4), (3.5) and taking $j\to \mathrm{\infty }$, we have

$$0<|a_1-a_2|=|g_j^{(k)}(z_j+{\rho }_j{\xi }_j)-g_j^{(k)}(z_j+{\rho }_j{\xi }_j^{\ast })|\to |g^{(k)}(0)-g^{(k)}(0)|.$$

It is a contradiction.

The proof of Theorem 1.8 is complete. □

Proof of Theorem 1.9 By Lemma 2.4, similar to the proof of Theorem 1.8, we can give the proof of Theorem 1.9. We omit the details.

The proof of Theorem 1.9 is complete. □

Proof of Theorem 1.10 and Theorem 1.11 Set ${\mathcal{F}}^{\ast }=\{\frac{f^{n+1}}{n+1}|f\in \mathcal{F}\}$, ${\mathcal{G}}^{\ast }=\{\frac{g^{n+1}}{n+1}|g\in \mathcal{G}\}$.

Noting that for each function $f^{\ast }\in {\mathcal{F}}^{\ast }$, all of whose zeros and poles are multiple if $n\notin \{-2,-1,0\}$, and all of whose zeros have multiplicities at least 3 if $n=-2$. For each $f^{\ast }\in {\mathcal{F}}^{\ast }$, there exists g in $\mathcal{G}$ such that ${(f^{\ast })}^{\prime }=a_i⟹{(g^{\ast })}^{\prime }=a_i$ for $i=1,2$ in D, we know that ${\mathcal{F}}^{\ast }$ is normal in D by Theorem 1.8 and Theorem 1.9. Therefore, ℱ is normal in D.

The proof of Theorem 1.10 and Theorem 1.11 is complete. □