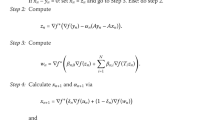Abstract
In this paper, we construct a new hybrid projection method for approximating a common element of the set of zeroes of a finite family of maximal monotone operators and the set of common solutions to a system of generalized equilibrium problems in a uniformly smooth and strictly convex Banach space. We prove strong convergence theorems of the algorithm to a common element of these two sets. As application, we also apply our results to find common solutions of variational inequalities and zeroes of maximal monotone operators.
MSC:47H05, 47H09, 47H10.
Similar content being viewed by others
1 Introduction
Let E be a Banach space with the norm and let denote the dual space of E. Let be the unit sphere of E. A Banach space E is said to be smooth if the limit
exists for any . E is said to be uniformly smooth if the limit (1.1) is attained uniformly for in . A Banach space E is said to be strictly convex if for all with and (see [1] for more details).
One of the major problems in the theory of monotone operators is as follows.
Find a point such that
where B is an operator from E into . Such is called a zero point of B. We denote the set of zeroes of the operator B by .
An operator is said to be monotone if
A monotone B is said to be maximal if its graph is not properly contained in the graph of any other monotone operator. If B is maximal monotone, then the solution set is closed and convex. The resolvent of a monotone operator B is defined by
Let C be a closed convex subset of a Banach space E, a mapping is said to be nonexpansive if
Recall that a point is a fixed point of T provided . Let E be a Banach space with dual and let be the pairing between E and . The normalized duality mapping is defined by
The Lyapunov functional is defined by
It is obvious that
If E is a Hilbert space, then for all .
A point p in C is said to be a strongly asymptotic fixed point of T [2] if C contains a sequence which converges strongly to p such that . The set of strong asymptotic fixed points of T will be denoted by .
A mapping T from C into itself is said to be a weak relatively nonexpansive mapping if
-
1.
is nonempty;
-
2.
for all and ;
-
3.
.
Kohasaka and Takahashi [3] proved that if E is a smooth strictly convex and reflexive Banach space and B is a continuous monotone operator with , then is a weak relatively nonexpansive mapping. By Takahashi [4], we know that is closed and convex, where is the set of fixed points of .
Let B be a maximal monotone operator in a Hilbert space H. The proximal point algorithm generates, for starting , a sequence in H by
where and .
Also, Rockafellar [5] proved that the sequence defined by (1.5) converges weakly to an element of .
Let C be a nonempty closed convex subset of E and let ℝ be the set of real numbers. Let be a bifunction and be a nonlinear mapping for . The system of generalized equilibrium problems is as follows.
Find such that for all ,
If and in (1.6), then from the problem (1.6) we have the following generalized equilibrium problem denoted by .
Find such that
The generalized equilibrium problems include fixed point problems, optimization problem, monotone inclusion problems, saddle point problems, variational inequality problems, minimization problems, vector equilibrium problems, Nash equilibria in noncooperative games and equilibrium problems as special cases (see, for example, [6]). Also, some solution methods have been proposed to solve the equilibrium problem (see, for example, [7–14]) and numerous problems in physics, optimization and economics reduce to finding a solution of problem (1.7).
Recently, Li and Su [15] introduced the hybrid iterative scheme for approximating a common solution of the equilibrium problems and the variational inequality problems in a 2-uniformly convex real Banach space which is also uniformly smooth. In 2010, Zegeye and Shahzad [16] introduced the iterative process which converges strongly to a common solution of the variational inequality problems for two monotone mappings in Banach spaces.
Quite recently, Shehu [13] introduced an iterative scheme by the hybrid method for approximating a common element of the set of zeroes of a finite family of α-inverse-strongly monotone operators and the set of common solutions of a system of generalized mixed equilibrium problems in a 2-uniformly convex real Banach space which is also uniformly smooth.
Motivated by the results of Shehu [13], we prove some strong convergence theorems for finding a common zero of a finite family of continuous monotone mappings and a solution of the system of generalized equilibrium problems in a uniformly smooth and strictly convex real Banach space with the Kadec-Klee property.
2 Preliminaries
Throughout this paper, let E be a Banach space with its dual space . For a sequence of E and a point , the weak convergence of to x is denoted by and the strong convergence of to x is denoted by .
The normalized duality mapping is defined by
where denotes the duality pairing.
Cioranescu [17] proved the following properties:
-
(1)
If E is an arbitrary Banach space, then J is monotone and bounded;
-
(2)
If E is a strictly convex, then J is strictly monotone;
-
(3)
If E is a smooth, then J is single-valued and semi-continuous;
-
(4)
If E is uniformly smooth, then J is uniformly norm-to-norm continuous on each bounded subset of E;
-
(5)
If E is reflexive, smooth and strictly convex, then the normalized duality mapping J is single-valued, one-to-one and onto;
-
(6)
If E is a reflexive, strictly convex and smooth Banach space and J is the duality mapping from E into , then is also single-valued, bijective and is also the duality mapping from into E and thus and ;
-
(7)
If E is uniformly smooth, then E is smooth and reflexive;
-
(8)
E is uniformly smooth if and only if is uniformly convex.
A Banach space E has the Kadec-Klee property [1, 17] if, for any sequence and with and , then as .
Consider the functional defined by
where J is the normalized duality mapping from E to .
It is obvious from the definition of the function ϕ that
If E is a Hilbert space, then .
Remark 2.1 If E is a reflexive, strictly convex and smooth Banach space, then, for any , if and only if . It is sufficient to show that if , then . From (1.4) we have . This implies that . From the definition of J, one has . Therefore, we have (see [1, 17] for more details).
Let C be a nonempty closed convex subset of a reflexive, strictly convex and smooth Banach space E. The generalized projection is a mapping that assigns to an arbitrary point the minimum point of the functional , that is, , where is the solution to the minimization problem
The existence and uniqueness of the operator follows from the properties of the functional and the strict monotonicity of the mapping J (see, for example, [1, 17–20]). If E is a Hilbert space, then becomes the metric projection of E onto C.
Example 2.2 (Qin et al. [21])
Let be the generalized projection from a smooth strictly convex and reflexive Banach space E onto a nonempty closed convex subset C of E. Then is a closed relatively quasi-nonexpansive mapping from E onto C with .
We also need the following lemmas for the proof of our main results.
Lemma 2.3 (Alber [19])
Let C be a nonempty closed convex subset of a smooth Banach space E and let . Then if and only if
Lemma 2.4 (Alber [19])
Let E be a reflexive, strictly convex and smooth Banach space, let C be a nonempty closed convex subset of E and let . Then
Let E be a smooth strictly convex and reflexive Banach space, C be a nonempty closed convex subset of E and be a monotone operator satisfying the following:
Then the resolvent of B is defined by
is a single-valued mapping from E to . For any , the Yosida approximation of B is defined by for all . We know that for all and .
Lemma 2.5 (Kohsaka and Takahashi [22])
Let E be a smooth strictly convex and reflexive Banach space, let C be a nonempty closed convex subset of E and let be a monotone operator satisfying . For any , let and be the resolvent and the Yosida approximation of B, respectively. Then the following hold:
-
(1)
for all and ;
-
(2)
for all ;
-
(3)
.
Lemma 2.6 (Rockafellar [23])
Let E be a reflexive strictly convex and smooth Banach space. Then an operator is maximal monotone if and only if for all .
For solving the equilibrium problem for a bifunction , assume that f satisfies the following conditions:
(A1) for all ;
(A2) f is monotone, i.e., for all ;
(A3) for each ,
(A4) for each , is convex and lower semi-continuous.
The following result is given in Blum and Oettli [6].
Lemma 2.7 Let C be a closed convex subset of a smooth strictly convex and reflexive Banach space E and let f be a bifunction from to ℝ satisfying the conditions (A1)-(A4). Then, for any and , there exists such that
Lemma 2.8 (Takahashi and Zembayashi [24])
Let C be a closed convex subset of a uniformly smooth strictly convex and reflexive Banach space E and let f be a bifunction from to ℝ satisfying the conditions (A1)-(A4). For any and , define a mapping as follows:
Then the following hold:
-
(1)
is single-valued;
-
(2)
is a firmly nonexpansive-type mapping for all , that is,
-
(3)
;
-
(4)
is closed and convex.
Lemma 2.9 (Takahashi and Zembayashi [24])
Let C be a closed convex subset of a smooth, strictly convex and reflexive Banach space E, f be a bifunction from to ℝ satisfying the conditions (A1)-(A4) and let . Then, for any and ,
Lemma 2.10 Let C be a nonempty closed convex subset of a smooth, strictly convex and reflexive Banach space E. Let be a continuous monotone mapping and f be a bifunction from to ℝ satisfying the conditions (A1)-(A4). Then, for any and , there exists such that
Proof Define a bifunction by for all . We show that Θ satisfies the conditions (A1)-(A4).
First, we show that Θ satisfies the condition (A1). Since
the condition (A2) is satisfied.
Next, we show that Θ satisfies the condition (A2). Since A is a continuous monotone mapping and f satisfies the condition (A2), for any , we have
So, the condition (A2) is satisfied.
Thirdly, we show that Θ satisfies the condition (A3). Since f satisfies the condition (A3) and A is a continuous monotone mapping, for any , we have
The condition (A3) is satisfied.
Finally, we show that Θ satisfies the condition (A4) since is convex and continuous; that is, is convex and lower semi-continuous. Since is convex and lower semi-continuous, is convex and lower semi-continuous.
Therefore, satisfies the conditions (A1)-(A4). From Lemma 2.7, we can conclude that there exists such that
This completes the proof. □
Lemma 2.11 Let C be a nonempty closed convex subset of a smooth, strictly convex and reflexive Banach space E. Let be a continuous and monotone mapping and f be a bifunction from to ℝ satisfying the conditions (A1)-(A4). Then, for any and , there exists such that
Define a mapping as follows:
Then we have the following:
-
(1)
is single-valued;
-
(2)
is firmly nonexpansive, i.e., for all ,
-
(3)
;
-
(4)
is closed and convex;
-
(5)
for all and .
Proof Define a bifunction by for all . From Lemma 2.8, it follows that Θ satisfies the conditions (A1)-(A4). Now, we can rewrite the mapping given in (2.4) as follows:
Thus, from Lemmas 2.8 and 2.9, we obtain the conclusion. This completes the proof. □
Throughout this paper, we define a mapping by
where for all and .
3 Main results
Theorem 3.1 Let C be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space E with the Kadec-Klee property. For any , let be a bifunction from to ℝ satisfying the conditions (A1)-(A4) and let be a finite family of continuous and monotone mappings from C to . Let be maximal monotone operators satisfying and for all and . Assume that . For arbitrary and , generate a sequence by
where for some for all and for all . Then the sequence converges strongly to a point , where .
Proof We split the proof into five steps as follows.
Step 1. We first show that is closed and convex for all . Clearly, is closed and convex. Suppose that is closed and convex for all . Since, for any , we know that is equivalent to the following:
Thus is closed and convex for all .
Step 2. We show that for all and is well defined. Since , suppose that for some . Let , from Lemma 2.11 and Lemma 2.5, we have that
This shows that , which implies that . Hence for all . This implies that the sequence is well defined.
Step 3. We show that and . By the definition of with and , it follows that
that is, is nondecreasing. By Lemma 2.4, we get
This implies that is bounded and so exists. In particular, by (1.4), the sequence is bounded. This implies is also bounded. So, and are also bounded. Since E is reflexive and is closed and convex, without loss of generality, we may assume that there exists such that .
Since , we have
On the other hand, since
it follows that
This implies that . Hence we get as . In view of the Kadec-Klee property of E, we obtain
Now, we claim that as . By the definition of , it follows that
Since exists, we obtain
Since and the definition of , we have . By (3.6) we also have
From (2.2) it follows that
Since J is uniformly norm-to-norm continuous on bounded subsets of E, it follows that
This implies that is bounded in . Note that E is reflexive and is also reflexive, we can assume that . Since E is reflexive, we see that . Hence there exists such that , and we have
Taking on both sides of the equation above, in view of the weak lower semi-continuity of the norm , it follows that
From Remark 2.1 we have , which implies that , and so . From the Kadec-Klee property, we have that
Note that is norm-weak∗-continuous, that is,
From (3.8), (3.10) and the Kadec-Klee property of E, it follows that
Since , it follows that
Since J is uniformly norm-to-norm continuous on bounded subsets of E, we obtain
Step 4. We show that . First, we show that . From (3.2), (3.5) and (3.11), it follows that for any ,
Denote for each and . We have that for all . From Lemma 2.5(1), it follows that
Taking limit as on both sides of the inequality, we have
From (2.2) it follows that . Since , we have
Since J is uniformly norm-to-norm continuous on bounded subsets of E, it follows that
This implies that is bounded in and is reflexive, we can assume that . In view of , there exists such that , and so
Taking on both sides of the equality above and in view of the weak lower semi-continuity of the norm , it follows that
From Remark 2.1, we have , which implies that and so . From (3.16) and the Kadec-Klee property of , we have as . Note that is norm-weak∗-continuous, that is, . From (3.15) and the Kadec-Klee property of E, we have
For any , we note that
Thus it follows from and that
Denote for each and . We can rewrite as . It follows that for each , we have
From Lemma 2.11(5), for each , we have
From (3.18) it follows that as for each , and so from (2.2), that
Since , we also have, for each ,
Since is bounded for each and E is reflexive, without loss of generality, we may assume that for all . From the first step, since is closed and convex for each , it is obvious that . Again, since
taking on both sides of the equality above, we have
This implies that for each , and so
From (3.21), (3.22) and the Kadec-Klee property, for each , we have
By using the triangle inequality, for each , we obtain
Hence, for each , we have
Since and J is uniformly norm-to-norm continuous on bounded subsets of E, for each , we have
From Lemma 2.11 we have, for each ,
where for all . From the condition (A2), it follows that for each ,
From (3.23) and (3.25), for each , we have
For any and , let . Then we get . From (3.26) it follows that for each ,
By the conditions (A1) and (A4), for each , we have
From the condition (A3), we get
Taking in the equality above, for each , we have
that is, for all and . This implies that for each . Therefore, .
Next, we show that . Let for each . For any , it follows that for each ,
By Lemma 2.5 we have, for ,
Since and as , we get as for . From (2.2) it follows that
Since , we also have
This implies that for each , is bounded and E is reflexive, without loss of generality, we assume that . We know that is closed and convex for each , it is obvious that . Again, since
taking on both sides of equality above, we have
That is, , , it follows that
From (3.31), (3.32) and the Kadec-Klee property, it follows that
We also have
It follows that
Since J is uniformly norm-to-norm continuous on bounded subsets of E and
for each , we have
Let for each . Then we have
For any and for each , it follows from the monotonicity of that for all ,
Letting in the inequality above, we get . Since is maximal monotone for each , we obtain .
Step 5. We show that . From , we have for all . Since , we also have
and so, taking limit , we get
Therefore, by Lemma 2.3, we can conclude that and as . The proof is completed. □
If and , we have the following.
Corollary 3.2 Let C be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space E with the Kadec-Klee property. Let f be a bifunction from to ℝ satisfying the conditions (A1)-(A4) and let be a continuous and monotone mapping. Let be a maximal monotone operator satisfying and for all . Assume that . For arbitrary and , generate a sequence by
where for some and . Then the sequence converges strongly to a point , where .
4 Applications
In this section, we apply our result to find a common solution of the variational inequality problems and zeros of the maximal operators.
We need the following lemma for our result, which is a special case of Lemmas 2.8 and 2.9 of [24].
Lemma 4.1 (Zegeye and Shahzad [16])
Let C be a closed convex subset of a uniformly smooth, strictly convex real Banach space E. Let be a continuous monotone mapping. For any and , define a mapping as follows:
Then we have the following:
-
(1)
is single-valued;
-
(2)
is a firmly nonexpansive-type mapping, i.e., for any ,
-
(3)
;
-
(4)
is closed and convex;
-
(5)
for any .
Theorem 4.2 Let C be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space E with the Kadec-Klee property. For each , let be a finite family of continuous and monotone mappings . For and , define a mapping by
Let be a maximal monotone operator satisfying and for all and . Assume that . For an initial point with , define the sequence in C as follows:
where for some for all and for all . Then the sequence converges strongly to a point , where .
Proof Taking for all in Theorem 3.1, we can get the desired conclusion. □
By Theorem 4.2, if we set for each , we obtain the following.
Corollary 4.3 Let C be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space E with the Kadec-Klee property. For any , let be a finite family of continuous and monotone mappings . Assume that . For an initial point with , define the sequence in C as follows:
where for some for each . Then the sequence converges strongly to a point , where .
Remark 4.4 Corollary 4.3 extends and improves the result of Zegeye and Shahzad [16] to a common solution of the variational inequality problems.
References
Takahashi W: Nonlinear Functional Analysis: Fixed Point Theory and Its Application. Yokohama-Publishers, Yokohama; 2000.
Reich S: A weak convergence theorem for the alternating method with Bregman distance. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Edited by: Kartsatos AG. Dekker, New York; 1996:313–318.
Kohsaka F, Takahashi W: Strong convergence of an iterative sequence for maximal monotone operator in Banach spaces. Abstr. Appl. Anal. 2004, 3: 239–249.
Takahashi W: Introduction to Nonlinear and Convex Analysis. Yokohama-Publishers, Yokohama; 2009.
Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 1976, 14: 877–898. 10.1137/0314056
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63: 123–145.
Kim JK: Strong convergence theorems by hybrid projection methods for equilibriums problems and fixed point problems of the asymptotically quasi- ϕ -nonexpansive mappings. Fixed Point Theory Appl. 2011., 2011: Article ID 10
Saewan S, Kumam P: Modified hybrid block iterative algorithm for convex feasibility problems and generalized equilibrium problems for uniformly quasi- ϕ -asymptotically nonexpansive mappings. Abstr. Appl. Anal. 2010., 2010: Article ID 357120
Saewan S, Kumam P: A hybrid iterative scheme for a maximal monotone operator and two countable families of relatively quasi-nonexpansive mappings for generalized mixed equilibrium and variational inequality problems. Abstr. Appl. Anal. 2010., 2010: Article ID 123027
Saewan S, Kumam P: The shrinking projection method for solving generalized equilibrium problem and common fixed points for asymptotically quasi- ϕ -nonexpansive mappings. Fixed Point Theory Appl. 2011., 2011: Article ID 9
Saewan S, Kumam P: Strong convergence theorems for countable families of uniformly quasi- ϕ -asymptotically nonexpansive mappings and a system of generalized mixed equilibrium problems. Abstr. Appl. Anal. 2011., 2011: Article ID 701675
Saewan S, Kumam P: A modified hybrid projection method for solving generalized mixed equilibrium problems and fixed point problems in Banach spaces. Comput. Math. Appl. 2011, 62: 1723–1735.
Shehu Y: Iterative approximation of zeroes of monotone operators and system of generalized mixed equilibrium problems. Optim. Lett. 2011. doi:10.1007/s11590–011–0343-x
Takahashi W, Zembayashi K: Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory Appl. 2008., 2008: Article ID 528476
Li Y, Su Y: Strong convergence theorem by a new hybrid method for equilibrium problems and variational inequality problems. Nonlinear Anal. 2010, 72: 847–855. 10.1016/j.na.2009.07.037
Zegeye H, Shahzad N: Approximating common solution of variational inequality problems for two monotone mappings in Banach spaces. Optim. Lett. 2011. doi:10.1007/s11590–010–0235–5
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems. Kluwer Academic, Dordrecht; 1990.
Alber YI, Reich S: An iterative method for solving a class of nonlinear operator equations in Banach spaces. Panam. Math. J. 1994, 4: 39–54.
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Edited by: Kartsatos AG. Dekker, New York; 1996:15–50.
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM J. Optim. 2002, 13: 938–945. 10.1137/S105262340139611X
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. J. Comput. Appl. Math. 2009, 225: 20–30. 10.1016/j.cam.2008.06.011
Kohsaka F, Takahashi W: Existence and approximation of fixed points of firmly nonexpansive type mappings in Banach spaces. SIAM J. Optim. 2008, 19: 824–835. 10.1137/070688717
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Trans. Am. Math. Soc. 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Anal. 2009, 70: 45–57. 10.1016/j.na.2007.11.031
Acknowledgements
This work was supported by Thaksin University Research Fund and was also supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant Number: 2012-0008170).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saewan, S., Kumam, P. & Cho, Y.J. Convergence theorems for finding zero points of maximal monotone operators and equilibrium problems in Banach spaces. J Inequal Appl 2013, 247 (2013). https://doi.org/10.1186/1029-242X-2013-247
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-247