Abstract
We establish some stability results for the cubic functional equations
and
in the setting of various  -fuzzy normed spaces that in turn generalize a Hyers-Ulam stability result in the framework of classical normed spaces. First, we shall prove the stability of cubic functional equations in the
-fuzzy normed spaces that in turn generalize a Hyers-Ulam stability result in the framework of classical normed spaces. First, we shall prove the stability of cubic functional equations in the  -fuzzy normed space under arbitrary t-norm which generalizes previous studies. Then, we prove the stability of cubic functional equations in the non-Archimedean
-fuzzy normed space under arbitrary t-norm which generalizes previous studies. Then, we prove the stability of cubic functional equations in the non-Archimedean  -fuzzy normed space. We therefore provide a link among different disciplines: fuzzy set theory, lattice theory, non-Archimedean spaces, and mathematical analysis.
-fuzzy normed space. We therefore provide a link among different disciplines: fuzzy set theory, lattice theory, non-Archimedean spaces, and mathematical analysis.
Mathematics Subject Classification (2000): Primary 54E40; Secondary 39B82, 46S50, 46S40.
Similar content being viewed by others
1. Introduction
The study of stability problems for functional equations is related to a question of Ulam [1] concerning the stability of group homomorphisms and it was affirmatively answered for Banach spaces by Hyers [2]. Subsequently, the result of Hyers was generalized by Aoki [3] for additive mappings and by Rassias [4] for linear mappings by considering an unbounded Cauchy difference. The article [4] of Rassias has provided a lot of influence in the development of what we now call Hyers-Ulam-Rassias stability of functional equations. For more informations on such problems, refer to the papers [5–15].
The functional equations
and
are called the cubic functional equations, since the function f(x) = cx3 is their solution. Every solution of the cubic functional equations is said to be a cubic mapping. The stability problem for the cubic functional equations was studied by Jun and Kim [16] for mappings f : X → Y, where X is a real normed space and Y is a Banach space. Later a number of mathematicians worked on the stability of some types of cubic equations [4, 17–19]. Furthermore, Mirmostafaee and Moslehian [20], Mirmostafaee et al. [21], Alsina [22], Miheţ and Radu [23] and others [24–28] investigated the stability in the settings of fuzzy, probabilistic, and random normed spaces.
2. Preliminaries
In this section, we recall some definitions and results which are needed to prove our main results.
A triangular norm (shorter t-norm) is a binary operation on the unit interval [0,1], i.e., a function T : [0,1] × [0,1] → [0,1] such that for all a, b, c ∈ [0,1] the following four axioms are satisfied:
-
(i)
T (a, b) = T (b, a) (: commutativity);
-
(ii)
T (a, (T (b, c))) = T (T (a, b), c) (: associativity);
-
(iii)
T (a, 1) = a (: boundary condition);
-
(iv)
T (a, b) ≤ T (a, c) whenever b ≤ c (: monotonicity).
Basic examples are the Lukasiewicz t-norm T L , T L (a, b) = max(a + b - 1, 0) ∀a, b ∈ [0,1] and the t-norms T P , T M , T D , where T P (a, b) := ab, T M (a, b) := min{a, b},
If T is a t-norm then is defined for every x ∈ [0,1] and n ∈ N ∪ {0} by 1, if n = 0 and if n ≥ 1. A t-norm T is said to be of Hadžić-type (we denote by T ∈  ) if the family is equicontinuous at x = 1 (cf. [29]).
) if the family is equicontinuous at x = 1 (cf. [29]).
Other important triangular norms are (see [30]):
-
the Sugeno-Weber family is defined by , and
if λ ∈ (-1, ∞).
-
the Domby family defined by TD, if λ = 0, TM, if λ = ∞ and
if λ ∈ (0, ∞).
-
the Aczel-Alsina family defined by TD, if λ = 0, TM, if λ = ∞ and
if λ ∈ (0, ∞).
A t-norm T can be extended (by associativity) in a unique way to an n-array operation taking for (x1, . . . , x n ) ∈ [0,1]n the value T (x1, . . . , x n ) defined by
T can also be extended to a countable operation taking for any sequence (x n ) n∈N in [0,1] the value
The limit on the right side of (2.1) exists, since the sequence is non-increasing and bounded from below.
Proposition 2.1. [30] (1) For T ≥ T L the following implication holds:
-
(2)
If T is of Hadžić-type then
for every sequence {x n }n∈Nin [0, 1] such that .
-
(3)
If , then
-
(4)
If , then
3.  -Fuzzy normed spaces
-Fuzzy normed spaces
The theory of fuzzy sets was introduced by Zadeh [31]. After the pioneering study of Zadeh, there has been a great effort to obtain fuzzy analogs of classical theories. Among other fields, a progressive development is made in the field of fuzzy topology [32–40, 43–50]. One of the problems in  -fuzzy topology is to obtain an appropriate concept of
-fuzzy topology is to obtain an appropriate concept of  -fuzzy metric spaces and
-fuzzy metric spaces and  -fuzzy normed spaces. Saadati and Park [40], respectively, introduced and studied a notion of intuitionistic fuzzy metric (normed) spaces and then Deschrijver et al. [41] generalized the concept of intuitionistic fuzzy metric (normed) spaces and studied a notion of
-fuzzy normed spaces. Saadati and Park [40], respectively, introduced and studied a notion of intuitionistic fuzzy metric (normed) spaces and then Deschrijver et al. [41] generalized the concept of intuitionistic fuzzy metric (normed) spaces and studied a notion of  -fuzzy metric spaces and
-fuzzy metric spaces and  -fuzzy normed spaces (also, see [41, 42, 51–55]). In this section, we give some definitions and related lemmas for our main results.
-fuzzy normed spaces (also, see [41, 42, 51–55]). In this section, we give some definitions and related lemmas for our main results.
In this section, we give some definitions and related lemmas which are needed later.
Definition 3.1 ([43]). Let be a complete lattice and U be a non-empty set called universe. A  -fuzzy set
-fuzzy set on U is defined as a mapping . For any u ∈ U, represents the degree (in L) to which u satisfies .
on U is defined as a mapping . For any u ∈ U, represents the degree (in L) to which u satisfies .
Lemma 3.2 ([44]). Consider the set L* and operation defined by:
and for all (x1, x2), (y1, y2) ∈ L*. Then (L*, ≤ L* ) is a complete lattice.
Definition 3.3 ([45]). An intuitionistic fuzzy set on a universe U is an object , where, for all u ∈ U, and are called the membership degree and the non-membership degree, respectively, of u in and, furthermore, satisfy.
In Section 2, we presented the classical definition of t-norm, which can be easily extended to any lattice . Define first and .
Definition 3.4. A triangular norm (t-norm) on  is a mapping satisfying the following conditions:
is a mapping satisfying the following conditions:
-
(i)
for any (: boundary condition);
-
(ii)
for any (: commutativity);
-
(iii)
for any (: associativity);
-
(iv)
for any and (: monotonicity).
A t-norm can also be defined recursively as an (n + 1)-array operation (n ∈ N \ {0}) by and
The t-norm M defined by
is a continuous t-norm.
Definition 3.5. A t-norm on L* is said to be t-representable if there exist a t-norm T and a t-conorm S on [0,1] such that
Definition 3.6. A negation on  is any strictly decreasing mapping satisfying and . If for all x ∈ L, then
is any strictly decreasing mapping satisfying and . If for all x ∈ L, then  is called an involutive negation.
is called an involutive negation.
In this article, let be a given mapping. The negation N s on ([0,1], ≤) defined as N s (x) = 1 - x for all x ∈ [0, 1] is called the standard negation on ([0,1], ≤).
Definition 3.7. The 3-tuple is said to be a  -fuzzy normed space if V is a vector space, is a continuous t-norm on
-fuzzy normed space if V is a vector space, is a continuous t-norm on  and
and  is a
is a  -fuzzy set on satisfying the following conditions: for all x, y ∈ V and t, s ∈]0, +∞[,
-fuzzy set on satisfying the following conditions: for all x, y ∈ V and t, s ∈]0, +∞[,
-
(i)
-
(ii)
if and only if x = 0;
-
(iii)
for all α ≠ 0;
-
(iv)
;
-
(v)
is continuous;
-
(vi)
and .
In this case,  is called a
is called a  -fuzzy norm. If is an intuitionistic fuzzy set and the t-norm is t-representable, then the 3-tuple is said to be an intuitionistic fuzzy normed space.
-fuzzy norm. If is an intuitionistic fuzzy set and the t-norm is t-representable, then the 3-tuple is said to be an intuitionistic fuzzy normed space.
Definition 3.8. (1) A sequence {x n } in X is called a Cauchy sequence if, for any and t > 0, there exists a positive integer n0 such that
-
(2)
If every Cauchy sequence is convergent, then the
 -fuzzy norm is said to be complete and the
-fuzzy norm is said to be complete and the  -fuzzy normed space is called a
-fuzzy normed space is called a  -fuzzy Banach space, where
-fuzzy Banach space, where 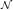 is an involutive negation.
is an involutive negation. -
(3)
The sequence {x n } is said to be convergent to x ∈ V in the
 -fuzzy normed space (denoted by if , whenever n → + ∞ for all t > 0.
-fuzzy normed space (denoted by if , whenever n → + ∞ for all t > 0.
Lemma 3.9 ([46]). Let be a  -fuzzy norm on V. Then
-fuzzy norm on V. Then
-
(1)
For all × ∈ V, is nondecreasing with respect to t.
-
(2)
for all x, y ∈ V and t ∈ ]0, +∞ [.
Definition 3.10. Let be a  -fuzzy normed space. For any t ∈ ]0, +∞[, we define the open ball B(x, r, t) with center x ∈ V and radius as
-fuzzy normed space. For any t ∈ ]0, +∞[, we define the open ball B(x, r, t) with center x ∈ V and radius as
4. Stability result in  -fuzzy normed spaces
-fuzzy normed spaces
In this section, we study the stability of functional equations in  -fuzzy normed spaces.
-fuzzy normed spaces.
Theorem 4.1. Let X be a linear space and be a complete  -fuzzy normed space. If f : × → Y is a mapping with f (0) = 0 and Q is a
-fuzzy normed space. If f : × → Y is a mapping with f (0) = 0 and Q is a  -fuzzy set on X2 × (0, ∞) with the following property:
-fuzzy set on X2 × (0, ∞) with the following property:
If
and
then there exists a unique cubic mapping C : X → Y such that
Proof. We brief the proof because it is similar as the random case [47, 27]. Putting y = 0 in (4.1), we have
Therefore, it follows that
By the triangle inequality, it follows that
In order to prove the convergence of the sequence , we replace x with 3mx in (4.3) to find that, for all m, n > 0,
Since the right-hand side of the inequality tends to as m tends to infinity, the sequence is a Cauchy sequence. Thus, we may define for all x ∈ X. Replacing x, y with 3nx and 3ny, respectively, in (4.1), it follows that C is a cubic mapping. To prove (4.2), take the limit as n → ∞ in (4.3). To prove the uniqueness of the cubic mapping C subject to (4.2), let us assume that there exists another cubic mapping C' which satisfies (4.2). Obviously, we have C(3nx) = 33nC(x) and C'(3nx) = 33nC'(x) for all x ∈ X and n ∈ ℕ. Hence it follows from (4.2) that
which proves the uniqueness of C. This completes the proof.
Theorem 4.2. Let X be a linear space and be a complete  -fuzzy normed space. If f : X → Y is a mapping with f (0) = 0 and Q is a
-fuzzy normed space. If f : X → Y is a mapping with f (0) = 0 and Q is a  -fuzzy set on X2 × (0, ∞) with the following property:
-fuzzy set on X2 × (0, ∞) with the following property:
If
and
then there exists a unique cubic mapping C : X → Y such that
Proof. We omit the proof because it is similar as the last theorem and see [28].
Corollary 4.3. Letbe  -fuzzy normed space and be a complete
-fuzzy normed space and be a complete  -fuzzy normed space. If f : X → Y is a mapping such that
-fuzzy normed space. If f : X → Y is a mapping such that
and
then there exists a unique cubic mapping C : X → Y such that
Proof. See [28].
Now, we give an example to validate the main result as follows:
Example 4.4 ([28]). Let (X, || · ||) be a Banach space, be an intuitionistic fuzzy normed space in which and
also be a complete intuitionistic fuzzy normed space. Define a mapping f : X → Y by f (x) = x3 + x0 for all x ∈ X, where x0 is a unit vector in X. A straightforward computation shows that
Also, we have
Therefore, all the conditions of Theorem 4.2 hold and so there exists a unique cubic mapping C : X → Y such that
5. Non-Archimedean L-fuzzy normed spaces
In 1897, Hensel [?] introduced a field with a valuation in which does not have the Archimedean property.
Definition 5.1. Let  be a field. A non-Archimedean absolute value on
be a field. A non-Archimedean absolute value on  is a function such that, for any a, b ∈ ,
is a function such that, for any a, b ∈ ,
-
(i)
|a| ≥ 0 and equality holds if and only if a = 0;
-
(ii)
|ab| = |a| |b|;
-
(iii)
|a + b| ≤ max {|a|, |b|} (: the strict triangle inequality).
Note that |n| ≤ 1 for each integer n ≥ 1. We always assume, in addition, that | · | is non-trivial, i.e., there exists a0 ∈  such that |a0| ≠ 0, 1.
such that |a0| ≠ 0, 1.
Definition 5.2. A non-Archimedean  -fuzzy normed space is a triple , where V is a vector space,
-fuzzy normed space is a triple , where V is a vector space,  is a continuous t-norm on
is a continuous t-norm on  and
and  is a
is a  -fuzzy set on V × ]0, +∞[ satisfying the following conditions: for all x, y ∈ V and t, s ∈ ]0, +∞[,
-fuzzy set on V × ]0, +∞[ satisfying the following conditions: for all x, y ∈ V and t, s ∈ ]0, +∞[,
-
(i)
;
-
(ii)
if and only if x = 0;
-
(iii)
for all α ≠ 0;
-
(vi)
;
-
(v)
is continuous;
-
(vi)
and .
Example 5.3. Let (X, || · ||) be a non-Archimedean normed linear space. Then the triple , where
is a non-Archimedean  -fuzzy normed space in which L = [0,1].
-fuzzy normed space in which L = [0,1].
Example 5.4. Let (X, ||·||) be a non-Archimedean normed linear space. Denote for all a = (a1, a2), b = (b1, b2) ∈ L* and be the intuitionistic fuzzy set on X × ]0, +∞[ defined as follows:
Then is a non-Archimedean intuitionistic fuzzy normed space.
6.  -fuzzy Hyers-Ulam-Rassias stability for cubic functional equations in non-Archimedean
-fuzzy Hyers-Ulam-Rassias stability for cubic functional equations in non-Archimedean -fuzzy normed space
-fuzzy normed space
Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over  . In this section, we investigate the stability of the cubic functional equation (1.1).
. In this section, we investigate the stability of the cubic functional equation (1.1).
Next, we define a  -fuzzy approximately cubic mapping. Let Ψ be a
-fuzzy approximately cubic mapping. Let Ψ be a  -fuzzy set on X × X × [0, ∞) such that Ψ (x, y, ·) is nondecreasing,
-fuzzy set on X × X × [0, ∞) such that Ψ (x, y, ·) is nondecreasing,
and
Definition 6.1. A mapping f : X → Y is said to be Ψ-approximately cubic if
Here, we assume that 3 ≠ 0 in  (i.e., characteristic of
(i.e., characteristic of  is not 3).
is not 3).
Theorem 6.2. Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over  : Let f: X → Y be a Ψ-approximately cubic mapping. If there exist a α ∈ ℝ (α > 0) and an integer k, k ≥ 2 with | 3k| < α and | 3| ≠ 1 such that
: Let f: X → Y be a Ψ-approximately cubic mapping. If there exist a α ∈ ℝ (α > 0) and an integer k, k ≥ 2 with | 3k| < α and | 3| ≠ 1 such that
and
then there exists a unique cubic mapping C : X → Y such that
where
Proof. First, we show, by induction on j, that, for all x ∈ X, t > 0 and j ≥ 1,
Putting y = 0 in (6.1), we obtain
This proves (6.4) for j = 1. Let (6.4) hold for some j > 1. Replacing y by 0 and x by 3jx in (6.1), we get
Since | 27| ≤ 1, it follows that
Thus (6.4) holds for all j ≥ 1. In particular, we have
Replacing x by 3-(kn+k)x in (6.5) and using the inequality (6.2), we obtain
and so
Hence, it follow that
Since for all x ∈ X and t > 0, is a Cauchy sequence in the non-Archimedean  -fuzzy Banach space . Hence we can define a mapping C : X → Y such that
-fuzzy Banach space . Hence we can define a mapping C : X → Y such that
Next, for all n ≥ 1, x ∈ X and t > 0, we have
and so
Taking the limit as n → ∞ in (6.7), we obtain
which proves (6.3). As  is continuous, from a well known result in
is continuous, from a well known result in  -fuzzy (probabilistic) normed space (see, [51, Chap. 12]), it follows that
-fuzzy (probabilistic) normed space (see, [51, Chap. 12]), it follows that
On the other hand, replacing x, y by 3-knx, 3-kny in (6.1) and (6.2), we get
Since , we infer that C is a cubic mapping.
For the uniqueness of C, let C' : X → Y be another cubic mapping such that
Then we have, for all x, y ∈ X and t > 0,
Therefore, from (6.6), we conclude that C = C'. This completes the proof.
Corollary 6.3. Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over  under a t-norm
under a t-norm . Let f: X → Y be a Ψ-approximately cubic mapping. If there exist α ∈ ℝ (α > 0),| 3| ≠ 1 and an integer k, k ≥ 3 with | 3k| < α such that
. Let f: X → Y be a Ψ-approximately cubic mapping. If there exist α ∈ ℝ (α > 0),| 3| ≠ 1 and an integer k, k ≥ 3 with | 3k| < α such that
then there exists a unique cubic mapping C : X → Y such that
where
Proof. Since
and  is of Hadžić type, it follows from Proposition 2.1 that
is of Hadžić type, it follows from Proposition 2.1 that
Now, if we apply Theorem 6.2, we get the conclusion.
Now, we give an example to validate the main result as follows:
Example 6.4. Let (X, || · ||) be a non-Archimedean Banach space, be non-Archimedean  -fuzzy normed space (intuitionistic fuzzy normed space) in which
-fuzzy normed space (intuitionistic fuzzy normed space) in which
and be a complete non-Archimedean  -fuzzy normed space (intuitionistic fuzzy normed space) (see, Example 5.4). Define
-fuzzy normed space (intuitionistic fuzzy normed space) (see, Example 5.4). Define
It is easy to see that (6.2) holds for α = 1. Also, since
we have
Let f : X → Y be a Ψ-approximately cubic mapping. Therefore, all the conditions of Theorem 6.2 hold and so there exists a unique cubic mapping C : X → Y such that
Definition 6.5. A mapping f : X → Y is said to be Ψ-approximately cubic I if
In this section, we assume that 2 ≠ 0 in  (i.e., the characteristic of
(i.e., the characteristic of  is not 2).
is not 2).
Theorem 6.6. Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over . Let f : X → Y be a Ψ-approximately cubic I mapping. If | 2| ≠ 1 and for some α ∈ ℝ, α > 0, and some integer k, k ≥ 2 with | 2k| < α,
. Let f : X → Y be a Ψ-approximately cubic I mapping. If | 2| ≠ 1 and for some α ∈ ℝ, α > 0, and some integer k, k ≥ 2 with | 2k| < α,
and
then there exists a unique cubic mapping C : X → Y such that
where
Proof. We omit the proof because it is similar as the random case (see, [28]).
Corollary 6.7. Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over  under a t-norm
under a t-norm  . Let f : X → Y be a Ψ-approximately cubic I mapping. If there exist a α ∈ ℝ (α > 0) and an integer k, k ≥ 2 with |2k| < α such that
. Let f : X → Y be a Ψ-approximately cubic I mapping. If there exist a α ∈ ℝ (α > 0) and an integer k, k ≥ 2 with |2k| < α such that
then there exists a unique cubic mapping C : X → Y such that
where
Proof. Since
and  is of Hadžić type, it follows from Proposition 2.1 that
is of Hadžić type, it follows from Proposition 2.1 that
Now, if we apply Theorem 6.2, we get the conclusion.
Now, we give an example to validate the main result as follows:
Example 6.8. Let (X, || · || be a non-Archimedean Banach space, be non-Archimedean  -fuzzy normed space (intuitionistic fuzzy normed space) in which
-fuzzy normed space (intuitionistic fuzzy normed space) in which
and be a complete non-Archimedean  -fuzzy normed space (intuitionistic fuzzy normed space) (see, Example 5.4). Define
-fuzzy normed space (intuitionistic fuzzy normed space) (see, Example 5.4). Define
It is easy to see that (6.9) holds for α = 1. Also, since
we have
Let f : X → Y be a Ψ-approximately cubic I mapping. Therefore, all the conditions of Theorem 6.6 hold and so there exists a unique cubic mapping C : X → Y such that
Definition 6.9. A mapping f : X → Y is said to be Ψ-approximately cubic II if
Here, we assume that 3 ≠ 0 in  (i.e., the characteristic of
(i.e., the characteristic of  is not 3).
is not 3).
Theorem 6.10. Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over  . Let f : X → Y be a Ψ-approximately cubic II function. If |3| ≠ 1 and, for some α ∈ ℝ, α > 0, and some integer k, k ≥ 3, with |3k| < α,
. Let f : X → Y be a Ψ-approximately cubic II function. If |3| ≠ 1 and, for some α ∈ ℝ, α > 0, and some integer k, k ≥ 3, with |3k| < α,
and
then there exists a unique cubic mapping C : X → Y such tha
for all × ∈ X and t > 0, where
Proof. First, we show, by induction on j, that, for all x ∈ X, t > 0 and j ≥ 1,
Put y = 0 in (6.11) to obtain
This proves (6.15) for j = 1. Let (6.15) hold for some j > 1. Replacing y by 0 and x by 3jx in (6.16), we get
Since |27| ≤ 1, then we have
Thus (6.15) holds for all j ≥ 1. In particular, it follows that
Replacing x by 3-(kn+k)x in (6.17) and using inequality (6.12) we obtain
Then we have
Hence we have
Since for all x ∈ X and t > 0, {kn f (k--nx)}
n∈N
is a Cauchy sequence in the non-Archimedean  -fuzzy Banach space Hence we can define a mapping C : X → Y such that
-fuzzy Banach space Hence we can define a mapping C : X → Y such that
Next, for all n ≥ 1, x ∈ X and t > 0,
Therefore, we have
By letting n → ∞ in the above inequality, we obtain
This proves (6.14). Since is continuous, from the well known result in  -fuzzy (probabilistic) normed space (see, [51, Chap. 12]), it follows that
-fuzzy (probabilistic) normed space (see, [51, Chap. 12]), it follows that
On the other hand, replace x, y by 3-knx, 3-kny in (6.11) and (6.12) to get
Since we infer that C is a cubic mapping.
If is another cubic mapping such that for all x ∈ X and t > 0, then, for all n ≥ 1, x ∈ X and t > 0,
Thus, from (6.20), we conclude that C = . This completes the proof.
Corollary 6.11. Let  be a non-Archimedean field, X be a vector space over
be a non-Archimedean field, X be a vector space over  and be a non-Archimedean
and be a non-Archimedean  -fuzzy Banach space over
-fuzzy Banach space over  under a t-norm T∈
under a t-norm T∈  . Let f : X → Y be a Ψ-approximately cubic II function. If, for some α ∈ ℝ, α > 0 and an integer k, k ≥ 3, with | 3k| < α,
. Let f : X → Y be a Ψ-approximately cubic II function. If, for some α ∈ ℝ, α > 0 and an integer k, k ≥ 3, with | 3k| < α,
then there exists a unique cubic mapping C : X → Y such that, for all × ∈ X and t > 0,
Where
Proof. Since
and T is of Hadžić type, from Proposition 2.1, it follows that
Thus, if we apply Theorem 6.10, then we can get the conclusion. This completes the proof.
7. Conclusion
We established the Hyers-Ulam-Rassias stability of the cubic functional equations (1.1), (1.2), and (1.3) in various fuzzy spaces. In Section 4, we proved the stability of functional equations (1.1), (1.2), and (1.3) in a  -fuzzy normed space under arbitrary t-norm which is a generalization of [26]. In Section 6, we proved the stability of functional equations (1.1), (1.2), and (1.3) in a non-Archimedean
-fuzzy normed space under arbitrary t-norm which is a generalization of [26]. In Section 6, we proved the stability of functional equations (1.1), (1.2), and (1.3) in a non-Archimedean  -fuzzy normed space. We therefore provided a link among three various discipline: fuzzy set theory, lattice theory, and mathematical analysis.
-fuzzy normed space. We therefore provided a link among three various discipline: fuzzy set theory, lattice theory, and mathematical analysis.
References
Ulam SM: Problems in Modern Mathematics, Chapter VI. Science Editions, Wiley, New York; 1964.
Hyers DH: On the stability of the linear functional equation. Proc Nat Acad Sci USA 1941, 27: 222–224.
Aoki T: On the stability of the linear transformation in Banach spaces. J Math Soc Japan 1950, 2: 64–66.
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proc Am Math Soc 1978, 72: 297–300.
Baak C, Moslehian MS: On the stability of J* -homomorphisms. Nonlinear Anal 2005, 63: 42–48.
Cho YJ, Gordji ME, Zolfaghari S: Solutions and stability of generalized mixed type QC functional equations in random normed spaces. J Inequal Appl 2010. Article ID 403101, 16 doi:10.1155/2010/403101
Cho YJ, Park C, Saadati R: Functional inequalities in non-Archimedean in Banach spaces. Appl Math Lett 2010, 60: 1994–2002.
Cho YJ, Park C, Sadaati R: Fuzzy functional inequalities. J Comput Anal Appl 2011, 13: 305–320.
Cho YJ, Rassias ThM, Park C, Saadati R: Inner product spaces and functional equations. J Comput Anal Appl 2011, 13: 296–304.
Czerwik S: Functional Equations and Inequalities in Several Variables. World Scientific, River Edge, NJ; 2002.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables. Birkhäuser, Basel; 1998.
Jung SM: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor; 2001.
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Appl Math 2000, 62: 23–130.
Rassias ThM: Functional Equations, Inequalities and Applications. Kluwer Academic Publishers, Dordrecht, Boston and London; 2003.
Miheţ D: Hyers-Ulam-Rassias stability for Jensen equation in non-Archimedean fuzzy normed spaces. In Proceedings of The Twelfth International Conference on Applied Mthematics and Computer Science, in Automat Comput Appl Math. Volume 17. Baisoara, Romania; 2008:5–13. September 10–13
Jun KW, Kim HM: The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. J Math Anal Appl 2002, 274: 867–878.
Jun KW, Kim HM, Chang IS: On the Hyers-Ulam stability of an Euler-Lagrange type cubic functional equation. J Comput Anal Appl 2005, 7: 21–33.
Baktash E, Cho YJ, Jalili M, Saadati R, Vaezpour SM: On the stability of cubic mappings and quadratic mappings in random normed spaces. J Inequal Appl 2008., 2008: Article ID 902187
Saadati R, Vaezpour SM, Cho YJ: A note on the "On the stability of cubic mappings and quadratic mappings in random normed spaces". J Inequal Appl 2009, 2009: Article ID 214530, 6.
Mirmostafaee AK, Moslehian MS: Fuzzy versions of Hyers-Ulam-Rassias theorem. Fuzzy Sets Syst 2008, 159: 720–729.
Mirmostafaee AK, Mirzavaziri M, Moslehian MS: Fuzzy stability of the Jensen functional equation. Fuzzy Sets Syst 2008, 159: 730–738.
Alsina C: On the stability of a functional equation arising in probabilistic normed spaces. General Inequalities 1987, 5: 263–271. Oberwolfach, 1986, Birkhäuser, Basel
Miheţ D Radu V: On the stability of the additive Cauchy functional equation in random normed spaces. J Math Anal Appl 2008, 343: 567–572.
Miheţ D, Saadati R, Vaezpour SM: The stability of the quartic functional equation in random normed spaces. Acta Appl Math doi:10.1007/s10440–009–9476–7
Shakeri S: Intuitionistic fuzzy stability of Jensen type mapping. J Nonlinear Sci Appl 2009, 2: 105–112.
Mirmostafaee AK, Moslehian MS: Fuzzy approximately cubic mappings. Inf Sci 2008, 178: 3791–3798.
Zhang S-S, Rassias JM, Saadati R: Stability of a cubic functional equation in intuitionistic random normed spaces. Appl Math Mech English edition. 2010, 31(1):21–26.
Saadati R, Vaezpour SM, Park C: The stability of the cubic functional equation in various spaces. Math Commun 2011, 16: 131–145.
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces. Kluwer Academic, Dordrecht; 2001.
Hadžić O, Pap E, Budincević M: Countable extension of triangular norms and their applications to the Fixed point theory in probabilistic metric spaces. Kybernetica 2002, 38: 363–381.
Zadeh LA: Fuzzy sets. Inf Control 1965, 8: 338–353.
Amini M, Saadati R: Topics in fuzzy metric space. J Fuzzy Math 2003, 4: 765–768.
George A, Veeramani P: On some result in fuzzy metric space. Fuzzy Sets Syst 1994, 64: 395–399.
George A, Veeramani P: On some result of analysis for fuzzy metric spaces. Fuzzy Sets Syst 1997, 90: 365–368.
Gregori V, Romaguera S: Some properties of fuzzy metric spaces. Fuzzy Sets Syst 2000, 115: 485–489.
Hosseini SB, Saadati R, Amini M: Alexandroff theorem in fuzzy metric spaces. Math Sci Res J 2004, 8: 357–361.
Saadati R, Vaezpour SM: Some results on fuzzy Banach spaces. J Appl Math Comput 2005, 17: 475–484.
Adibi H, Cho YJ, O'Regan D, Saadati R: Common Fixed point theorems in -fuzzy metric spaces. Appl Math Comput 2006, 182: 820–828.
Sintunavarat W, Cho YJ, Kumam P: Couple coincidence point theorems for contractions without commutative condition in intuitionistic fuzzy normed spaces. Fixed Point Theory Appl 2011, 81.
Saadati R, Park J: On the intuitionistic fuzzy topological spaces. Chaos, Solitons and Fractals 2006, 27: 331–344.
Deschrijver G, O'Regan D, Saadati R, Vaezpour SM: L -Fuzzy Euclidean normed spaces and compactness. Chaos, Soliton and Fractals 2009, 42: 40–45.
Saadati R: On the -fuzzy topological spaces. Chaos, Solitons and Fractals 2008, 37: 1419–1426.
Goguen J: -fuzzy sets. J Math Anal Appl 1967, 18: 145–174.
Deschrijver G, Kerre EE: On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst 2003, 23: 227–235.
Atanassov KT: Intuitionistic fuzzy sets. Fuzzy Sets Syst 1986, 20: 87–96.
Saadati R: A note on "Some results on the IF-normed spaces". Chaos, Solitons and Fractals 2009, 41: 206–213.
Agarwal RP, Cho YJ, Saadati R: On random topological structures. Abstr Appl Anal, Art ID 2011. 762361, 41
Krishna SV, Sarma KKM: Separation of fuzzy normed linear spaces. Fuzzy Sets Syst 1994, 63: 207–217.
Xiao JZ, Zhu XH: Fuzzy normed spaces of operators and its completeness. Fuzzy Sets Syst 2003, 133: 389–399.
Katsaras AK: Fuzzy topological vector spaces II. Fuzzy Sets Syst 1984, 12: 143–154.
Schweizer B, Sklar A: Probabilistic Metric Spaces. Elsevier, North Holand, New York; 1983.
Bag T, Samanta SK: Finite dimensional fuzzy normed linear spaces. J Fuzzy Math 2003, 11(3):687–705.
Biswas R: Fuzzy inner product spaces and fuzzy norm functions. Inf Sci 1991, 53: 185–190.
Felbin C: Finite dimensional fuzzy normed linear space. Fuzzy Sets Syst 1992, 48: 239–248.
Kramosil I, Michalek J: Fuzzy metric and statistical metric spaces. Kybernetica 1975, 11: 326–334.
Acknowledgment
This study was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant Number: 2011-0021821).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R.P., Cho, Y.J., Saadati, R. et al. Nonlinear  -Fuzzy stability of cubic functional equations.
J Inequal Appl 2012, 77 (2012). https://doi.org/10.1186/1029-242X-2012-77
-Fuzzy stability of cubic functional equations.
J Inequal Appl 2012, 77 (2012). https://doi.org/10.1186/1029-242X-2012-77
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-77



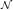 is an involutive negation.
is an involutive negation.