Duality for nondifferentiable multiobjective higher-order symmetric programs over cones involving generalized $(F,\alpha ,\rho ,d)$-convexity

Abstract

In this paper, a pair of Wolfe type higher-order symmetric nondifferentiable multiobjective programs over arbitrary cones is formulated and appropriate duality relations are then established under higher-order-K-$(F,\alpha ,\rho ,d)$-convexity assumptions. A numerical example which is higher-order K-$(F,\alpha ,\rho ,d)$-convex but not higher-order K-F-convex has also been illustrated. Special cases are also discussed to show that this paper extends some of the known works that have appeared in the literature.

MSC: 90C29, 90C30, 49N15.

1 Introduction

Mangasarian [1] introduced the concept of second- and higher-order duality for nonlinear problems. He has also indicated that the study is significant due to the computational advantage over the first-order duality as it provides tighter bounds for the value of the objective function when approximations are used. Motivated by the concept in [1], several researchers [2–19] have worked in this field.

Multiobjective optimization has a large number of applications. As an example, it is generally used in goal programming, risk programming etc. Optimality conditions for multiobjective programming problems can be found in Miettinen [20] and Pardalos et al. [21]. Recently, Chinchuluun and Pardalos [22] discussed recent developments in multiobjective optimization. These include optimality conditions, applications, global optimization techniques, the new concept of epsilon pareto optimal solutions and heuristics.

Chen [7] considered a pair of symmetric higher-order Mond-Weir type nondifferentiable multiobjective programming problems and established usual duality results under higher-order F-convexity assumptions. Gulati and Gupta [9] proved duality theorems for a pair of Wolfe type higher-order nondifferentiable symmetric dual programs. Ahmad et al. [6] formulated a general Mond-Weir type higher-order dual for a nondifferentiable multiobjective programming problem and established usual duality results.

Gulati and Geeta [23] pointed out certain omissions in some papers on symmetric duality in multiobjective programming and discussed their corrective measures. Later on, Ahmad and Husain [5] and Gulati et al. [11] formulated second-order multiobjective symmetric dual programs with cone constraints and established duality results under second-order invexity assumptions. An omission in the strong duality theorem in Yang et al. [17] has been rectified in Gupta and Kailey [12].

The concept of $(F,\rho )$-convexity was introduced by Preda [24] as an extension of F-convexity [25] and ρ-convexity [26]. Yang et al. [18] formulated several second-order duals for scalar programming problem and proved duality results involving generalized F-convex functions. Zhang and Mond [19] extended the class of $(F,\rho )$-convex functions to second-order and obtained duality relations for multiobjective dual problems.

Motivated by various concepts of generalized convexity, Liang et al. [27] introduced a unified formulation of generalized convexity, called $(F,\alpha ,\rho ,d)$-convexity and obtained corresponding optimality conditions and duality relations for a single objective fractional problem. This was later on extended to multiobjective fractional programming problem in Liang et al. [28]. Inspired by the concept given in [19, 27, 28], Ahmad and Husain [29] introduced second-order $(F,\alpha ,\rho ,d)$-convex functions and proved duality relations for Mond-Weir type second-order multiobjective problems. In the recent work of Ahmad and Husain [30], an attempt is made to remove certain omissions and inconsistencies in the work of Mishra and Lai [31].

Agarwal et al. [2] achieved duality results for a pair of Mond-Weir type multiobjective higher-order symmetric dual programs over arbitrary cones under higher-order K-F-convexity assumptions. Recently, Agarwal et al. [32] have filled some gap in the work of Chen [7] and proved a strong duality theorem for Mond-Weir type multiobjective higher-order nondifferentiable symmetric dual programs.

In this paper, we formulate a pair of symmetric higher-order Wolfe type nondifferentiable multiobjective programs over arbitrary cones and prove weak, strong and converse duality theorems under higher-order-K-$(F,\alpha ,\rho ,d)$-convexity assumptions. We also give a nontrivial example of a function lying in the class of higher-order K-$(F,\alpha ,\rho ,d)$-convex but not in the class of higher-order K-F-convex. Our study extends some of the known results that appeared in [4, 8, 16, 17].

2 Notations and preliminaries

Consider the following multiobjective programming problem:

$$\begin{array}{r}K\text{-minimize}\varphi (x)\\ \text{subject to}x\in X^0=\{x\in S:-g(x)\in C\},\end{array}$$

(P)

where $S\subseteq R^n$ is open, $\varphi :S\to R^k$, $g:S\to R^m$, K is a closed convex pointed cone in $R^k$ with $intK\ne \varphi$ and C is a closed convex cone in $R^m$ with nonempty interior.

Definition 1 [33]

The positive polar cone $C^{\ast }$ of C is defined as

$$C^{\ast }=\{z:{\xi }^{T}z\geqq 0,\text{ for all }\xi \in C\}.$$

Definition 2 [33]

A point $\overline{x}\in X^0$ is a weak efficient solution of (P) if there exists no other $x\in X^0$ such that

$$\varphi (\overline{x})-\varphi (x)\in intK.$$

Definition 3 [34]

A point $\overline{x}\in X^0$ is an efficient solution of (P) if there exists no other $x\in X^0$ such that

$$\varphi (\overline{x})-\varphi (x)\in K\mathrm{\setminus }\{0\}.$$

Definition 4 [2, 9, 16]

Let D be a compact convex set in $R^n$. The support function of D is defined by

$$S(x\mid D)=max\{x^{T}y:y\in D\}.$$

A support function, being convex and everywhere finite, has a subdifferential, that is, there exists $z\in R^n$ such that

$$S(y\mid D)\geqq S(x\mid D)+z^T(y-x)\text{for all }y\in D.$$

The subdifferential of $S(x\mid D)$ is given by

$$\partial S(x\mid D)=\{z\in D:z^{T}x=S(x\mid D)\}.$$

For any set $S\subset R^n$, the normal cone to S at a point $x\in S$ is defined by

$$N_S(x)=\{y\in R^n:y^T(z-x)\leqq 0\text{ for all }z\in S\}.$$

It can be easily seen that for a compact convex set D, y is in $N_D(x)$ if and only if $S(y\mid D)=x^{T}y$, or equivalently, x is in $\partial S(y\mid D)$.

Definition 5 [24, 28]

A functional $F:X\times X\times R^n\mapsto R$ (where $X\subseteq R^n$) is sublinear with respect to the third variable if, for all $(x,u)\in X\times X$,

(i) $F(x,u;a_1+a_2)\leqq F(x,u;a_1)+F(x,u;a_2)$ for all $a_1,a_2\in R^n$, and

(ii) $F(x,u;\alpha a)=\alpha F(x,u;a)$, for all $\alpha \in R_{+}$ and $a\in R^n$.

For notational convenience, we write

$$F(x,u;a)=F_{x,u}(a).$$

Let $F:S\times S\times R^n\mapsto R$ be a sublinear functional with respect to the third variable. Now, we recall the concept of higher-order K-F-convexity introduced in [2].

Definition 6 A differentiable function $\varphi :S\to R^k$ is said to be higher-order K-F-convex at u on S with respect to $\zeta :S\times R^n\mapsto R^k$ if, for all $x\in S$ and $q\in R^n$, we have

Remark 1

(i) If $K=R_{+}^k$, then the above definition reduces to higher-order F-convexity given in [7, 9, 32].

(ii) If $K=R_{+}^k$ and ${\zeta }_i(u,q)=\frac{1}{2}{q}^T{\mathrm{\nabla }}_{xx}{\varphi }_i(u)q$, $i=1,2,\dots ,k$, then Definition 6 becomes second-order F-convexity as considered in [12, 17].

(iii) Taking $K=R_{+}^k$, ${\zeta }_i(u,q)=\frac{1}{2}{q}^T{\mathrm{\nabla }}_{xx}{\varphi }_i(u)q$ and $F_{x,u}(a)=\eta {(x,u)}^{T}a$, then the definition reduces to second-order invexity (or η bonvexity) given in [5, 11, 15].

Definition 7 A differentiable function $\varphi :S\to R^k$ is said to be higher-order K-$(F,\alpha ,\rho ,d)$-convex at u on S with respect to $\zeta :S\times R^n\mapsto R^k$ if for all $x\in S$ and $q\in R^n$, there exist vector $\rho \in R^k$, a real valued function $\alpha :S\times S\to R_{+}\mathrm{\setminus }\{0\}$ and $d:S\times S\to R^k$ such that

Remark 2

(i) If $K=R_{+}$, $\alpha (x,u)=1$ and ${\zeta }_i(u,q)=\frac{1}{2}{q}^T{\mathrm{\nabla }}_{xx}{\varphi }_i(u)q$, $i=1,2,\dots ,k$, the definition of higher-order K-$(F,\alpha ,\rho ,d)$-convexity reduces to second-order $(F,\rho )$-convexity given by Srivastava and Bhatia [14].

(ii) If $K=R_{+}$, $\alpha (x,u)=1$ and $\rho =0$, then Definition 7 reduces to higher-order F-convexity (see [7, 9]).

(iii) If we take $K=R_{+}^1$, $\alpha (x,u)=1$, $\rho =0$, ${\zeta }_1(u,q)=\frac{1}{2}{q}^T{\mathrm{\nabla }}_{xx}{\varphi }_1(u)q$ and $F_{x,u}(a)=\eta {(x,u)}^{T}a$, where η is a function from $S\times S$ to $R^n$, then the above definition becomes second-order η-convexity given in [15].

Next, we illustrate a nontrivial example of higher-order K-$(F,\alpha ,\rho ,d)$-convex functions which are not higher-order K-F-convex.

Example 1 Let $X=[-2.5,-0.5]\subset R$, $n=m=1$, $k=2$, $K=\{(x,y):x\geqq 0,y\geqq 0\}$. Consider the function $\psi :X\to R^2$ to be defined by $\psi (x)=({\psi }_1(x),{\psi }_2(x))$, where

$${\psi }_1(x)=x^{3}sin\frac{2}{x},{\psi }_2(x)=x^3,$$

and $\alpha :X\times X\to R_{+}\mathrm{\setminus }\{0\}$ to be identified by $\alpha (x,u)=(u^2+1)$. Let the functional $F:X\times X\times R\to R$ be defined by

$$F_{x,u}(a)=12(1-u)a.$$

Suppose $d:X\times X\to R^2$ is given by $d(x,u)=(d_1(x,u),d_2(x,u))$, where

$$d_1(x,u)={(x^4+u^2)}^{\frac{3}{2}},d_2(x,u)={(x^2+u^2)}^{\frac{5}{2}}$$

and $\zeta :X\times R\to R^2$ is defined by $\zeta (u,q)=({\zeta }_1(u,q),{\zeta }_2(u,q))$, where

$${\zeta }_1(u,q)=15u+12q,{\zeta }_2(u,q)={sin}^{2}u+q^2.$$

To show ψ is higher-order $(F,\alpha ,\rho ,d)$-convex, we need to prove

$$\begin{array}{rcl}L& =& \{{\psi }_1(x)-{\psi }_1(u)-{\zeta }_1(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_1(u,q)\\ -F_{x,u}[\alpha (x,u)({\mathrm{\nabla }}_x{\psi }_1(u)+{\mathrm{\nabla }}_q{\zeta }_1(u,q))]\\ -{\rho }_1{d}_1^2(x,u),{\psi }_2(x)-{\psi }_2(u)-{\zeta }_2(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_2(u,q)\\ -F_{x,u}[\alpha (x,u)({\mathrm{\nabla }}_x{\psi }_2(u)+{\mathrm{\nabla }}_q{\zeta }_2(u,q))]-{\rho }_2{d}_2^2(x,u)\}\in K,\end{array}$$

which for ${\rho }_1=-4$ and ${\rho }_2=-28$ gives

$$\begin{array}{rcl}L& =& \{x^{3}sin\frac{2}{x}-u^{3}sin\frac{2}{u}-15u-12(1-u)\left[(u^2+1)(-2ucos\frac{2}{u}+3u^{2}sin\frac{2}{u}+12)\right]\\ +4{(x^4+u^2)}^3,x^3-u^3-{sin}^{2}u+q^2-12(1-u)\left[(u^2+1)(3u^2+2q)\right]\\ +28{(x^2+u^2)}^5\}\in K\\ =& \{L_1,L_2\}\in K,\end{array}$$

where

$$\begin{array}{rcl}{L}_1& =& x^{3}sin\frac{2}{x}-u^{3}sin\frac{2}{u}-15u-12(1-u)\left[(u^2+1)(-2ucos\frac{2}{u}+3u^{2}sin\frac{2}{u}+12)\right]\\ +4{(x^4+u^2)}^3\\ \geqq & 0\mathrm{\forall }x,u\in X\text{ as can be seen from Figure 1}\end{array}$$

(E1)

and

$$\begin{array}{rcl}{L}_2& =& x^3-u^3-{sin}^{2}u+q^2-12(1-u)\left[(u^2+1)(3u^2+2q)\right]+28{(x^2+u^2)}^5\\ =& L_{21}+L_{22}.\end{array}$$

But

$$\begin{array}{rcl}{L}_{21}& =& x^3-u^3-{sin}^{2}u-12(1-u)\left[3u^2(u^2+1)\right]+28{(x^2+u^2)}^5\\ \geqq & 0\mathrm{\forall }x,u\in X\text{ as can be seen from Figure 2}\end{array}$$

(E2)

and

$$\begin{array}{rcl}{L}_{22}& =& q^2-12(1-u)\left[2q(u^2+1)\right]\\ \geqq & 0\mathrm{\forall }u\in X\text{ and }q\in (-{10}^{18},{10}^{18})\text{ as can be seen from Figure 3.}\end{array}$$

(E3)

Hence, $L_2\geqq 0$. Therefore, ψ is higher-order K-$(F,\alpha ,\rho ,d)$-convex with respect to ζ.

Figure 1

Graph of ${\mathit{L}}_{\mathbf{1}}$ (Expression ( E1 )) against x and u .

Figure 2

Graph of ${\mathit{L}}_{\mathbf{21}}$ (Expression ( E2 )) against x and u .

Figure 3

Graph of ${\mathit{L}}_{\mathbf{22}}$ (Expression ( E3 )) against q and u .

Next, we need to show that ψ is not higher-order K-F-convex with respect to ζ. To prove it, we will show that

$$\begin{array}{rcl}M& =& \{{\psi }_1(x)-{\psi }_1(u)-{\zeta }_1(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_1(u,q)-F_{x,u}[{\mathrm{\nabla }}_x{\psi }_1(u)+{\mathrm{\nabla }}_q{\zeta }_1(u,q)],\\ {\psi }_2(x)-{\psi }_2(u)-{\zeta }_2(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_2(u,q)-F_{x,u}[{\mathrm{\nabla }}_x{\psi }_2(u)+{\mathrm{\nabla }}_q{\zeta }_2(u,q)]\}\notin K\end{array}$$

i.e., either

$${\psi }_1(x)-{\psi }_1(u)-{\zeta }_1(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_1(u,q)-F_{x,u}[{\mathrm{\nabla }}_x{\psi }_1(u)+{\mathrm{\nabla }}_q{\zeta }_1(u,q)]\geqq ̸0$$

or

$${\psi }_2(x)-{\psi }_2(u)-{\zeta }_2(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_2(u,q)-F_{x,u}[{\mathrm{\nabla }}_x{\psi }_2(u)+{\mathrm{\nabla }}_q{\zeta }_2(u,q)]\geqq ̸0.$$

Since

$$\begin{array}{rcl}M& =& {\psi }_1(x)-{\psi }_1(u)-{\zeta }_1(u,q)+q^T{\mathrm{\nabla }}_q{\zeta }_1(u,q)-F_{x,u}[{\mathrm{\nabla }}_x{\psi }_1(u)+{\mathrm{\nabla }}_q{\zeta }_1(u,q)]\\ =& x^{3}sin\frac{2}{x}-u^{3}sin\frac{2}{u}-15u-12(1-u)[-2ucos\frac{2}{u}+3u^{2}sin\frac{2}{u}+12]\\ =& -181.7330<0(\text{for }x=-2\text{ and }u=-1).\end{array}$$

(E4)

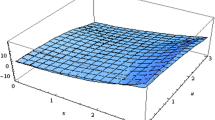
In fact, $M<0$ for all $x,u\in X$ as can be seen from Figure 4. Therefore, ψ is not higher-order K-F-convex with respect to ζ.

Figure 4

Graph of M (Expression ( E4 )) against x and u .

3 Wolfe type higher-order symmetric duality

In this section, we consider the following Wolfe type nondifferentiable multiobjective higher-order symmetric dual programs.

Primal problem (HNWP) K-minimize

$$\begin{array}{rcl}G(x,y,\lambda ,p)& =& f(x,y)+S(x\mid D)e_k+\left({\lambda }^{T}h\right)(x,y,p)e_k-p^T{\mathrm{\nabla }}_p\left({\lambda }^{T}h\right)(x,y,p)e_k\\ -y^T{\mathrm{\nabla }}_y\left({\lambda }^{T}f\right)(x,y)e_k-y^T{\mathrm{\nabla }}_p\left({\lambda }^{T}h\right)(x,y,p)e_k\end{array}$$

subject to

(1)

(2)

(3)

(4)

Dual problem (HNWD) K-maximize

$$\begin{array}{rcl}H(u,v,\lambda ,r)& =& f(u,v)-S(v\mid E)e_k+\left({\lambda }^{T}g\right)(u,v,r)e_k-r^T{\mathrm{\nabla }}_r\left({\lambda }^{T}g\right)(u,v,r)e_k\\ -u^T{\mathrm{\nabla }}_x\left({\lambda }^{T}f\right)(u,v)e_k-u^T{\mathrm{\nabla }}_r\left({\lambda }^{T}g\right)(u,v,r)e_k\end{array}$$

subject to

(5)

(6)

(7)

(8)

where

(i) $C_1$ and $C_2$ are closed convex cones with nonempty interiors in $R^n$ and $R^m$, respectively,

(ii) $S_1\subseteq R^n$ and $S_2\subseteq R^m$ are open sets such that $C_1\times C_2\subset S_1\times S_2$,

(iii) $f:S_1\times S_2\to R^k$, $h:S_1\times S_2\times R^m\to R^k$ and $g:S_1\times S_2\times R^n\to R^k$ are differentiable functions, $e_k={(1,\dots ,1)}^T\in R^k$, $\lambda \in R^k$,

(iv) r and p are vectors in $R^n$ and $R^m$, respectively,

(v) D and E are compact convex sets in $R^n$ and $R^m$, respectively, and

(vi) $S(x\mid D)$ and $S(v\mid E)$ are the support functions of D and E, respectively.

Remark 3 The problems (HNWP) and (HNWD) stated above are nondifferentiable because their objective function contains the support function $S(x\mid D)$ and $S(v\mid E)$.

We now prove the following duality results for the pair of problems (HNWP) and (HNWD).

Theorem 1 (Weak duality)

Let $(x,y,\lambda ,z,p)$ be feasible for the primal problem (HNWP) and $(u,v,\lambda ,w,r)$ be feasible for the dual problem (HNWD). Let the sublinear functionals $F:R^n\times R^n\times R^n\mapsto R$ and $G:R^m\times R^m\times R^m\mapsto R$ satisfy the following conditions:

(A)

(B)

Suppose that (i) either ${\sum }_{i=1}^k{\lambda }_i[{\rho }_i^{(1)}{(d_i^{(1)}(x,u))}^2+{\rho }_i^{(2)}{(d_i^{(2)}(v,y))}^2]\geqq 0$ or ${\rho }^{(1)}\geqq 0$ and ${\rho }^{(2)}\geqq 0$, (ii) $f(\cdot ,v)+{(\cdot )}^{T}w{e}_k$ is higher-order K-$(F,{\alpha }_1,{\rho }^{(1)},d^{(1)})$-convex at u with respect to $g(u,v,r)$, and (iii) $-\{f(x,\cdot )-{(\cdot )}^{T}z{e}_k\}$ is higher-order K-$(G,{\alpha }_2,{\rho }^{(2)},d^{(2)})$-convex at y with respect to $-h(x,y,p)$. Then

$$G(x,y,\lambda ,p)-H(u,v,\lambda ,r)\notin -K\mathrm{\setminus }\{0\}.$$

(9)

Proof Since $f(\cdot ,v)+{(\cdot )}^{T}w{e}_k$ is higher-order K-$(F,{\alpha }_1,{\rho }^{(1)},d^{(1)})$-convex with respect to $g(u,v,r)$, we have

It follows from $\lambda \in int{K}^{\ast }$, ${\lambda }^T{e}_k=1$, and sublinearity of F that

(10)

As $-\{f(x,\cdot )-{(\cdot )}^{T}z{e}_k\}$ is higher-order K-$(G,{\alpha }_2,{\rho }^{(2)},d^{(2)})$-convex with respect to $-h(x,y,p)$, therefore we get

Again, using $\lambda \in int{K}^{\ast }$, ${\lambda }^T{e}_k=1$, and sublinearity of G, we obtain

(11)

Further, adding the inequalities (10) and (11), we have

(12)

Now, since $(x,y,\lambda ,z,p)$ is feasible for the primal problem (HNWP) and $(u,v,\lambda ,w,r)$ is feasible for the dual problem (HNWD), ${\alpha }_1(x,u)>0$, by the dual constraint (5), the vector $a={\alpha }_1(x,u)[{\mathrm{\nabla }}_x({\lambda }^{T}f)(u,v)+w+{\mathrm{\nabla }}_r({\lambda }^{T}g)(u,v,r)]\in C_1^{\ast }$, and so from the hypothesis (A), we obtain

$$F_{x,u}(a)+{\alpha }_1^{-1}{a}^{T}u\geqq 0.$$

(13)

Similarly,

$$G_{v,y}(b)+{\alpha }_2^{-1}{b}^{T}y\geqq 0,$$

(14)

for the vector $b=-{\alpha }_2(v,y)[{\mathrm{\nabla }}_y({\lambda }^{T}f)(x,y)-z+{\mathrm{\nabla }}_p({\lambda }^{T}h)(x,y,p)]\in C_2^{\ast }$.

Using (13), (14) and the hypothesis (i) in (12), we have

Further, substituting the values of a and b, we have

In view of the fact that $x^{T}w\leqq S(x\mid D)$, $v^{T}z\leqq S(v\mid E)$ and ${\lambda }^T{e}_k=1$, the last inequality yields

(15)

Now, suppose contrary to the result that (9) does not hold, that is,

$$G(x,y,\lambda ,p)-H(u,v,\lambda ,r)\in -K\mathrm{\setminus }\{0\},$$

or

It follows from $\lambda \in int{K}^{\ast }$ and ${\lambda }^T{e}_k=1$ that

which contradicts (15). Hence the result. □

Theorem 2 (Strong duality)

Let $f:S_1\times S_2\to R^k$ be a twice differentiable function and let $(\overline{x},\overline{y},\overline{\lambda },\overline{z},\overline{p})$ be a weak efficient solution of (HNWP). Suppose that

(i) the matrix ${\mathrm{\nabla }}_{pp}({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})$ is nonsingular,

(ii) the vectors $\{{\mathrm{\nabla }}_y{f}_1(\overline{x},\overline{y}),\dots ,{\mathrm{\nabla }}_y{f}_k(\overline{x},\overline{y})\}$ are linearly independent,

(iii) the vector $\{{\mathrm{\nabla }}_y({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})-{\mathrm{\nabla }}_p({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})+{\mathrm{\nabla }}_{yy}({\overline{\lambda }}^{T}f)(\overline{x},\overline{y})\overline{p}\}\notin span\{{\mathrm{\nabla }}_y{f}_1(\overline{x},\overline{y}),\dots ,{\mathrm{\nabla }}_y{f}_k(\overline{x},\overline{y})\}\mathrm{\setminus }\{0\}$,

(iv) ${\mathrm{\nabla }}_y({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})-{\mathrm{\nabla }}_p({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})+{\mathrm{\nabla }}_{yy}({\overline{\lambda }}^{T}f)(\overline{x},\overline{y})\overline{p}=0$ implies $\overline{p}=0$,

(v) $({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},0)=({\overline{\lambda }}^{T}g)(\overline{x},\overline{y},0)$, ${\mathrm{\nabla }}_y({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},0)=0$, ${\mathrm{\nabla }}_p({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},0)=0$, ${\mathrm{\nabla }}_x({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},0)={\mathrm{\nabla }}_r({\overline{\lambda }}^{T}g)(\overline{x},\overline{y},0)$ and

(vi) K is a closed convex pointed cone with $R_{+}^k\subseteq K$.

Then

(I) there exists $\overline{w}\in D$ such that $(\overline{x},\overline{y},\overline{\lambda },\overline{w},\overline{r}=0)$ is feasible for (HNWD), and

(II) $G(\overline{x},\overline{y},\overline{\lambda },\overline{p})=H(\overline{x},\overline{y},\overline{\lambda },\overline{r})$.

Also, if the hypotheses of Theorem 1 are satisfied for all feasible solutions of (HNWP) and (HNWD), then $(\overline{x},\overline{y},\overline{\lambda },\overline{w},\overline{r}=0)$ is an efficient solution for (HNWD).

Proof Since $(\overline{x},\overline{y},\overline{\lambda },\overline{z},\overline{p})$ is a weak efficient solution of (HNWP), by the Fritz John necessary optimality conditions [33], there exist $\overline{\alpha }\in K^{\ast }$, $\overline{\beta }\in C_2$, $\overline{\eta }\in R$, such that the following conditions are satisfied at $(\overline{x},\overline{y},\overline{\lambda },\overline{z},\overline{p})$:

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

From (18) and nonsingularity of ${\mathrm{\nabla }}_{pp}({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})$, we have

$$\overline{\beta }=\left({\overline{\alpha }}^T{e}_k\right)(\overline{y}+\overline{p}).$$

(25)

Also, (19) is equivalent to

$${\mathrm{\nabla }}_{y}f(\overline{x},\overline{y})[\overline{\beta }-\left({\overline{\alpha }}^T{e}_k\right)\overline{y}]+h(\overline{x},\overline{y},\overline{p})\left({\overline{\alpha }}^T{e}_k\right)+\overline{\eta }{e}_k+{\mathrm{\nabla }}_{p}h(\overline{x},\overline{y},\overline{p})[\overline{\beta }-\left({\overline{\alpha }}^T{e}_k\right)(\overline{y}+\overline{p})]=0.$$

If $\overline{\alpha }=0$, then (25) yields $\overline{\beta }=0$. Further, the above equality gives $\overline{\eta }{e}_k=0$ or $\overline{\eta }=0$. Consequently, $(\overline{\alpha },\overline{\beta },\overline{\eta })=0$, contradicting (24). Hence, $\overline{\alpha }\ne 0$.

Since $R_{+}^k\subseteq K\Rightarrow K^{\ast }\subseteq R_{+}^k$, therefore $\overline{\alpha }\in K^{\ast }\Rightarrow \overline{\alpha }\geqq 0$.

But $\overline{\alpha }\ne 0\Rightarrow \overline{\alpha }\ge 0$ or

$${\overline{\alpha }}^T{e}_k>0.$$

(26)

Now, using (25) and (26) in (17), we get

(27)

which, by the hypotheses (iii) and (iv), implies

$$\overline{p}=0.$$

(28)

Using the hypothesis (iii) in (27), we obtain

$${\mathrm{\nabla }}_{y}f(\overline{x},\overline{y})[\overline{\alpha }-\left({\overline{\alpha }}^T{e}_k\right)\overline{\lambda }]=0.$$

Since the vectors $\{{\mathrm{\nabla }}_y{f}_1(\overline{x},\overline{y}),\dots ,{\mathrm{\nabla }}_y{f}_k(\overline{x},\overline{y})\}$ are linearly independent, therefore the above equation yields

$$\overline{\alpha }=\left({\overline{\alpha }}^T{e}_k\right)\overline{\lambda }.$$

(29)

From (28) in (25), we get

$$\overline{\beta }=\left({\overline{\alpha }}^T{e}_k\right)\overline{y}.$$

(30)

Using (26) and (28)-(30) in (16), we have

$$\{{\mathrm{\nabla }}_x\left({\overline{\lambda }}^{T}f\right)(\overline{x},\overline{y})+\overline{\gamma }+{\mathrm{\nabla }}_x\left({\overline{\lambda }}^{T}h\right)(\overline{x},\overline{y},\overline{p})\}(x-\overline{x})\geqq 0,\text{for all }x\in C_1.$$

From the hypothesis (v), for $\overline{r}=0$, the above inequality yields

$$\{{\mathrm{\nabla }}_x\left({\overline{\lambda }}^{T}f\right)(\overline{x},\overline{y})+\overline{\gamma }+{\mathrm{\nabla }}_r\left({\overline{\lambda }}^{T}g\right)(\overline{x},\overline{y},\overline{r})\}(x-\overline{x})\geqq 0.$$

(31)

Let $x\in C_1$. Then $x+\overline{x}\in C_1$, and so (31) implies

$${\{{\mathrm{\nabla }}_x\left({\overline{\lambda }}^{T}f\right)(\overline{x},\overline{y})+\overline{\gamma }+{\mathrm{\nabla }}_r\left({\overline{\lambda }}^{T}g\right)(\overline{x},\overline{y},\overline{r})\}}^{T}x\geqq 0,\text{for all }x\in C_1.$$

Therefore,

$$\{{\mathrm{\nabla }}_x\left({\overline{\lambda }}^{T}f\right)(\overline{x},\overline{y})+\overline{\gamma }+{\mathrm{\nabla }}_r\left({\overline{\lambda }}^{T}g\right)(\overline{x},\overline{y},\overline{r})\}\in C_1^{\ast }.$$

(32)

Also, from (26), (30) and $\overline{\beta }\in C_2$, we obtain $\overline{y}\in C_2$. Thus $(\overline{x},\overline{y},\overline{\lambda },\overline{w}=\overline{\gamma },\overline{r}=0)$, satisfies the dual constraints from (5) to (8) in (HNWD), and so it is a feasible solution for the dual problem (HNWD). Now, letting $x=0$ and $x=2\overline{x}$ in (31), we get

(33)

From (22) and (30), $({\overline{\alpha }}^T{e}_k)\overline{y}\in N_E(\overline{z})$. Since ${\overline{\alpha }}^T{e}_k>0$, $\overline{y}\in N_E(\overline{z})$. Also, as E is a compact convex set in $R^m$, ${\overline{y}}^T\overline{z}=S(\overline{y}\mid E)$.

Further, from (20), (26) and (30) and the above relation, we obtain

$${\overline{y}}^T[{\mathrm{\nabla }}_y\left({\overline{\lambda }}^{T}f\right)(\overline{x},\overline{y})+{\mathrm{\nabla }}_p\left({\overline{\lambda }}^{T}h\right)(\overline{x},\overline{y},\overline{p})]={\overline{y}}^T\overline{z}=S(\overline{y}\mid E).$$

(34)

Therefore, using (28), (33), (34) and the hypothesis (v), for $\overline{r}=0$, we get

that is, the two objective values are equal.

Now, let $(\overline{x},\overline{y},\overline{\lambda },\overline{w},\overline{r}=0)$ be not an efficient solution of (HNWD), then there exists $(\overline{u},\overline{v},\overline{\lambda },\overline{w},\overline{r}=0)$ feasible for (HNWD) such that

As ${\overline{x}}^T[{\mathrm{\nabla }}_x({\overline{\lambda }}^{T}f)(\overline{x},\overline{y})+{\mathrm{\nabla }}_r({\overline{\lambda }}^{T}g)(\overline{x},\overline{y},\overline{r})]=-S(\overline{x}\mid D)$, ${\overline{y}}^T[{\mathrm{\nabla }}_y({\overline{\lambda }}^{T}f)(\overline{x},\overline{y})+{\mathrm{\nabla }}_p({\overline{\lambda }}^{T}h)(\overline{x},\overline{y},\overline{p})]=S(\overline{y}\mid E)$ and from the hypothesis (v), for $\overline{r}=0$, we obtain

which contradicts Theorem 1. Hence, $(\overline{x},\overline{y},\overline{\lambda },\overline{w},\overline{r}=0)$ is an efficient solution of (HNWD). □

Theorem 3 (Converse duality)

Let $f:S_1\times S_2\to R^k$ be a twice differentiable function and let $(\overline{u},\overline{v},\overline{\lambda },\overline{w},\overline{r})$ be a weak efficient solution of (HNWD). Suppose that

(i) the matrix ${\mathrm{\nabla }}_{rr}({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},\overline{r})$ is nonsingular,

(ii) the vectors $\{{\mathrm{\nabla }}_x{f}_1(\overline{u},\overline{v}),\dots ,{\mathrm{\nabla }}_x{f}_k(\overline{u},\overline{v})\}$ are linearly independent,

(iii) the vector $\{{\mathrm{\nabla }}_x({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},\overline{r})-{\mathrm{\nabla }}_r({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},\overline{r})+{\mathrm{\nabla }}_{xx}({\overline{\lambda }}^{T}f)(\overline{u},\overline{v})\overline{r}\}\notin span\{{\mathrm{\nabla }}_x{f}_1(\overline{u},\overline{v}),\dots ,{\mathrm{\nabla }}_x{f}_k(\overline{u},\overline{v})\}\mathrm{\setminus }\{0\}$,

(iv) ${\mathrm{\nabla }}_x({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},\overline{r})-{\mathrm{\nabla }}_r({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},\overline{r})+{\mathrm{\nabla }}_{xx}({\overline{\lambda }}^{T}f)(\overline{u},\overline{v})\overline{r}=0$ implies $\overline{r}=0$,

(v) $({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},0)=({\overline{\lambda }}^{T}h)(\overline{u},\overline{v},0)$, ${\mathrm{\nabla }}_x({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},0)=0$, ${\mathrm{\nabla }}_r({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},0)=0$, ${\mathrm{\nabla }}_y({\overline{\lambda }}^{T}g)(\overline{u},\overline{v},0)={\mathrm{\nabla }}_p({\overline{\lambda }}^{T}h)(\overline{u},\overline{v},0)$ and

(vi) K is a closed convex pointed cone with $R_{+}^k\subseteq K$.

Then

(I) there exists $\overline{z}\in E$ such that $(\overline{u},\overline{v},\overline{\lambda },\overline{z},\overline{p}=0)$ is feasible for (HNWP), and

(II) $G(\overline{u},\overline{v},\overline{\lambda },\overline{p})=H(\overline{u},\overline{v},\overline{\lambda },\overline{r})$.

Also, if the hypotheses of Theorem 1 are satisfied for all feasible solutions of (HNWP) and (HNWD), then $(\overline{u},\overline{v},\overline{\lambda },\overline{z},\overline{p}=0)$ is an efficient solution for (HNWP).

Proof It follows on the lines of Theorem 2. □

4 Special cases

In this section, we consider some of the special cases of the problems studied in Section 3. In all these cases, $K=R_{+}^k$, $C_1=R_{+}^n$, $C_2=R_{+}^m$, $({\lambda }^{T}h)(x,y,p)=\frac{1}{2}{p}^T{\mathrm{\nabla }}_{yy}({\lambda }^{T}f)(x,y)p$ and $({\lambda }^{T}g)(u,v,r)=\frac{1}{2}{r}^T{\mathrm{\nabla }}_{xx}({\lambda }^{T}f)(u,v)r$.

(i) For $k=1$, $D=\{Ay:y^{T}Ay\leqq 1\}$, $E=\{Bx:x^{T}Bx\leqq 1\}$, where A and B are positive semidefinite matrices, ${(x^{T}Ax)}^{1/2}=S(x\mid D)$ and ${(y^{T}By)}^{1/2}=S(y\mid E)$. In this case, (HNWP) and (HNWD) reduce to the problems considered in Ahmad and Husain [4].

(ii) Let $k=1$, $D=\{0\}$ and $E=\{0\}$, then our problems (HNWP) and (HNWD) become the problems studied in Gulati et al. [8].

(iii) If $k=1$, then our problems (HNWP) and (HNWD) reduce to the programs studied in Yang et al. [16].

(iv) Let $D=\{0\}$ and $E=\{0\}$, our problems reduce to (MP) and (MD) considered in Yang et al. [17] along with nonnegativity restrictions $x\geqq 0$ and $v\geqq 0$. However, taking $F_{x,u}(a)={(x-u)}^{T}a$ and $G_{v,y}(b)={(v-y)}^{T}b$ along with the hypotheses (A) and (B) of Theorem 1 in [17] gives $x\geqq 0$ and $v\geqq 0$.

5 Conclusions

A pair of Wolfe-type multiobjective higher-order symmetric dual programs involving nondifferentiable functions over arbitrary cones has been formulated. Further, an example of higher-order K-$(F,\alpha ,\rho ,d)$-convex which is not higher-order K-F-convex has been illustrated. Weak, strong and converse duality theorems under higher-order K-$(F,\alpha ,\rho ,d)$-convexity assumptions have also been established. It is to be noted that some of the known results, including those of Ahmad and Husain [4], Gulati et al. [8] and Yang et al. [16, 17], are special cases of our study. This work can be further extended to study nondifferentiable higher-order multiobjective symmetric dual programs over arbitrary cones with different $p_i$’s and different support functions.