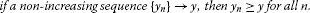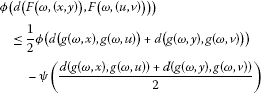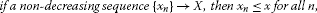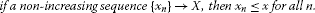Weak contractive inequalities and compatible mixed monotone random operators in ordered metric spaces

Abstract

The aim of this work is to define the notion of compatible random operators in a partially ordered metric space and prove some coupled random coincidence theorems for a pair of compatible mixed monotone random operators satisfying $(\varphi ,\phi )$-weak contractive conditions. These results present random versions and extensions of recent results of Ćirić and Lakshmikantham (Stoch. Anal. Appl. 27:1246-1259, 2009), Choudhury and Kundu (Nonlinear Anal. 73:2524-2531, 2010), Alotaibi and Alsulami (Fixed Point Theory Appl. 2011:44, 2011) and many others.

1 Introduction

Random coincidence point theorems are stochastic generalizations of classical coincidence point theorems. Some random fixed point theorems play an important role in the theory of random differential and random integral equations (see [1, 2]). Random fixed point theorems for contractive mappings on separable complete metric spaces have been proved by several authors [3–8]. Sehgal and Singh [9] have proved different stochastic versions of the well-known Schauder fixed point theorem. Fixed point theorems for monotone operators in ordered Banach spaces have been investigated and have found various applications in differential and integral equations (see [10–12] and references therein). Fixed point theorems for mixed monotone mappings in partially ordered metric spaces are of great importance and have been utilized for matrix equations, ordinary differential equations, and for the existence and uniqueness of solutions for some boundary value problems (see [13–19]).

Recently Ćirić and Lakshmikantham [20] and Zhu and Xiao [21] proved some coupled random fixed point and coupled random coincidence results in partially ordered complete metric spaces. The purpose of this article is to improve these results for a pair of compatible mixed monotone random mappings $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$, where F and g satisfy the $(\varphi ,\phi )$-weak contractive conditions. Presented results are also the extensions and improvements of the corresponding results in [22–24] and many others.

2 Preliminaries

Recall that if $(X,\le )$ is a partially ordered set and $F:X\to X$ is such that for $x,y\in X$, $x\le y$ implies $F(x)\le F(y)$, then a mapping F is said to be non-decreasing. Similarly, a non-increasing map may be defined. Bhaskar and Lakshmikantham [25] introduced the following notions of a mixed monotone mapping and a coupled fixed point.

Definition 2.1 ([25])

Let $(X,\le )$ be a partially ordered set and $F:X\times X\to X$. The mapping F is said to have the mixed monotone property if F is monotone non-decreasing in its first argument and is monotone non-increasing in its second argument, that is, for any $x,y\in X$,

$$x_1,x_2\in X;x_1\le x_2\Rightarrow F(x_1,y)\le F(x_2,y)$$

and

$$y_1,y_2\in X;y_1\le y_2\Rightarrow F(x,y_1)\ge F(x,y_2).$$

Definition 2.2 ([25])

An element $(x,y)\in X\times X$ is called a coupled fixed point of the mapping $F:X\times X\to X$ if

$$F(x,y)=x,F(y,x)=y.$$

The concept of the mixed monotone property is generalized in [24].

Definition 2.3 ([24])

Let $(X,\le )$ be a partially ordered set and $F:X\times X\to X$ and $g:X\to X$. The mapping F is said to have the mixed g-monotone property if F is monotone g-non-decreasing in its first argument and is monotone g-non-increasing in its second argument, that is, for any $x,y\in X$,

$$x_1,x_2\in X;g(x_1)\le g(x_2)\Rightarrow F(x_1,y)\le F(x_2,y)$$

and

$$y_1,y_2\in X;g(y_1)\le g(y_2)\Rightarrow F(x,y_1)\ge F(x,y_2).$$

Definition 2.4 An element $(x,y)\in X\times X$ is called a coupled fixed point of the mapping $F:X\times X\to X$ and $g:X\to X$ if

$$F(x,y)=g(x),F(y,x)=g(y).$$

Definition 2.5 The mappings F and g, where $F:X\times X\to X$ and $g:X\to X$, are said to be compatible if

$$\underset{n\to \mathrm{\infty }}{lim}d(g(F(x_n,y_n)),F(g(x_n),g(y_n)))=0$$

and

$$\underset{n\to \mathrm{\infty }}{lim}d(g(F(y_n,x_n)),F(g(y_n),g(x_n)))=0,$$

whenever $\{x_n\}$, $\{y_n\}$ are sequences in X such that ${lim}_{n\to \mathrm{\infty }}F(x_n,y_n)={lim}_{n\to \mathrm{\infty }}g(x_n)=x$ and ${lim}_{n\to \mathrm{\infty }}F(y_n,x_n)={lim}_{n\to \mathrm{\infty }}g(y_n)=y$ for all $x,y\in X$ are satisfied.

Using the concept of compatible maps and the mixed g-monotone property, Choudhury and Kundu [23] proved the following theorem.

Theorem 2.6 Let $(X,\le )$ be a partially ordered set, and let there be a metric d on X such that $(X,d)$ is a complete metric space. Let $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ be such that $\phi (t)<t$ and $limi{t}_{r\to t^{+}}\phi (r)<t$ for all $t>0$. Let $F:X\times X\to X$ and $g:X\to X$ be two mappings such that F has the mixed g-monotone property and satisfy

$$d(F(x,y),F(u,v))\le \phi \left(\frac{d(gx,gu)+d(gy,gv)}{2}\right)$$

for all $x,y,u,v\in X$, for which $gx\le gu$ and $gy\ge gv$. Let $F(X\times X)\subseteq g(X)$, g be continuous and monotone increasing and F and g be compatible mappings. Also, suppose either

• (a) F is continuous or

• (b) X has the following properties:

• (i) if a non-decreasing sequence $\{x_n\}\to x$, then $x_n\le x$ for all $n\ge 0$,

• (ii) if a non-increasing sequence $\{y_n\}\to y$, then $y_n\ge y$ for all $n\ge 0$.

If there exist $x_0,y_0\in X$, such that $g(x_0)\le F(x_0,y_0)$ and $g(y_0)\ge F(y_0,x_0)$, then there exist $x,y\in X$ such that $g(x)=F(x,y)$ and $g(y)=F(y,x)$, that is, F and g have a coupled coincidence point in X.

As in [17], let Φ denote all functions $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ which satisfy

• 1. ϕ is continuous and non-decreasing,

• 2. $\varphi (t)=0$ if and only if $t=0$,

• 3. $\varphi (t+s)\le \varphi (t)+\varphi (s)$, $\mathrm{\forall }t,s\in [0,\mathrm{\infty })$,

and let Ψ denote all the functions $\psi :[0,\mathrm{\infty })\to (0,\mathrm{\infty })$ which satisfy ${lim}_{t\to r}\psi (t)>0$ for all $r>0$ and ${lim}_{t\to 0^{+}}\psi (t)=0$.

Alotaibi and Alsulami in [22] proved the following coupled coincidence result for monotone operators in partially ordered metric spaces.

Theorem 2.7 Let $(X,\le )$ be a partially ordered set and suppose there is a metric d on X such that $(X,d)$ is a complete metric space. Let $F:X\times X\to X$ be a mapping having the mixed g-monotone property on X such that there exist two elements $x_0,y_0\in X$ with

$$g{x}_0\le F(x_0,y_0)\mathit{\text{and}}g{y}_0\ge F(y_0,x_0).$$

Suppose there exist $\varphi \in \mathrm{\Phi }$ and $\phi \in \mathrm{\Psi }$ such that

$$\varphi \left(d(F(x,y),F(u,v))\right)\le \frac{1}{2}\varphi (d(gx,gu)+d(gy,gv))-\psi \left(\frac{d(gx,gu)+d(gy,gv)}{2}\right)$$

for all $x,y,u,v\in X$ with $gx\ge gu$ and $gy\le gv$. Suppose $F(X\times X)\subseteq g(X)$, g is continuous and compatible with F and also suppose either

• (a) F is continuous or

• (b) X has the following property:

• (i) if a non-decreasing sequence $\{x_n\}\to x$, then $x_n\le x$ for all n,

• (ii) if a non-increasing sequence $\{y_n\}\to y$, then $y\le y_n$ for all n.

Then there exists $x,y\in X$ such that

$$gx=F(x,y)\mathit{\text{and}}gy=F(y,x)$$

that is, F and g have a coupled coincidence point in X.

3 Main results

Let $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space with Σ being a sigma algebra of subsets of Ω, and let $(X,d)$ be a metric space. A mapping $T:\mathrm{\Omega }\to X$ is called Σ-measurable if for any open subset U of X, $T^{-1}(U)=\{\omega :T(\omega )\in U\}\in \mathrm{\Sigma }$. In what follows, when we speak of measurability, we will mean Σ-measurability. A mapping $T:\mathrm{\Omega }\times X\to X$ is called a random operator if for any $x\in X$, $T(\cdot ,x)$ is measurable. A measurable mapping $\zeta :\mathrm{\Omega }\to X$ is called a random fixed point of a random function $T:\mathrm{\Omega }\times X\to X$ if $\zeta (\omega )=T(\omega ,\zeta (\omega ))$ for every $\omega \in \mathrm{\Omega }$. A measurable mapping $\zeta :\mathrm{\Omega }\to X$ is called a random coincidence of $T:\mathrm{\Omega }\times X\to X$ and $g:\mathrm{\Omega }\times X\to X$ if $g(\omega ,\zeta (\omega ))=T(\omega ,\zeta (\omega ))$ for every $\omega \in \mathrm{\Omega }$.

Definition 3.1 Let $(X,d)$ be a separable metric space and $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space. Then $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ are said to be compatible random operators if

$$\underset{n\to \mathrm{\infty }}{lim}d(g(\omega ,F(\omega ,(x_n,y_n))),F(\omega ,(g(\omega ,x_n),g(\omega ,y_n))))=0$$

and

$$\underset{n\to \mathrm{\infty }}{lim}d(g(\omega ,F(\omega ,(y_n,x_n))),F(\omega ,(g(\omega ,y_n),g(\omega ,x_n))))=0$$

whenever $\{x_n\}$, $\{y_n\}$ are sequences in X, such that ${lim}_{n\to \mathrm{\infty }}F(\omega ,(x_n,y_n))={lim}_{n\to \mathrm{\infty }}g(\omega ,x_n)=x$ and ${lim}_{n\to \mathrm{\infty }}F(\omega ,(y_n,x_n))={lim}_{n\to \mathrm{\infty }}g(\omega ,y_n)=y$ for all $\omega \in \mathrm{\Omega }$ and $x,y\in X$ are satisfied.

As in [23], let $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ be such that $\phi (t)<t$ and $limi{t}_{r\to t^{+}}\phi (r)<t$ for all $t>0$.

Now, we state our main result.

Theorem 3.2 Let $(X,\le ,d)$ be a complete separable partially ordered metric space, $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space, and $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ be mappings such that

• (i) $g(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$;

• (ii) $F(\cdot ,v)$, $g(\cdot ,x)$ are measurable for all $v\in X\times X$ and $x\in X$ respectively;

• (iii) $F(\omega ,\cdot )$ has the mixed $g(\omega ,\cdot )$-monotone property for each $\omega \in \mathrm{\Omega }$ and

  $$d(F(\omega ,(x,y)),F(\omega ,(u,v)))\le \phi \left(\frac{d(g(\omega ,x),g(\omega ,u))+d(g(\omega ,y),g(\omega ,v))}{2}\right)$$

  (1)

for all $x,y,u,v\in X$, for which $g(\omega ,x)\le g(\omega ,u)$ and $g(\omega ,y)\ge g(\omega ,v)$ for all $\omega \in \mathrm{\Omega }$.

Suppose $g(\omega \times X)=X$ for each $\omega \in \mathrm{\Omega }$, g is monotone increasing, and F and g are compatible random operators. Also suppose either

• (a) $F(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$ or

• (b) X has the following property:

  

  (2)
  

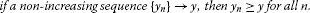  (3)

If there exist measurable mappings ${\zeta }_0,{\eta }_0:\mathrm{\Omega }\to X$ such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$, then there are measurable mappings $\zeta ,\theta :\mathrm{\Omega }\to X$ such that $F(\omega ,(\zeta (\omega ),\theta (\omega )))=g(\omega ,\zeta (\omega ))$ and $F(\omega ,(\theta (\omega ),\zeta (\omega )))=g(\omega ,\theta (\omega ))$ for all $\omega \in \mathrm{\Omega }$, that is, F and g have a coupled random coincidence point.

Proof Let $\mathrm{\Theta }=\{\zeta :\mathrm{\Omega }\to X\}$ be a family of measurable mappings. Define a function $h:\mathrm{\Omega }\times X\to R^{+}$ as follows:

$$h(\omega ,x)=d(x,g(\omega ,x)).$$

Since $x\to g(\omega ,x)$ is continuous for all $\omega \in \mathrm{\Omega }$, we conclude that $h(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$. Also, since $x\to g(\omega ,x)$ is measurable for all $x\in X$, we conclude that $h(\cdot ,x)$ is measurable for all $\omega \in \mathrm{\Omega }$ (see [26], p.868). Thus, $h(\omega ,x)$ is the Caratheodory function. Therefore, if $\zeta :\mathrm{\Omega }\to X$ is a measurable mapping, then $\omega \to h(\omega ,\zeta (\omega ))$ is also measurable (see [27]). Also, for each $\zeta \in \mathrm{\Theta }$, the function $\eta :\mathrm{\Omega }\to X$ defined by $\eta (\omega )=g(\omega ,\zeta (\omega ))$ is measurable, that is, $\eta \in \mathrm{\Theta }$.

Now, we shall construct two sequences of measurable mappings $\{{\zeta }_n\}$ and $\{{\eta }_n\}$ in Θ, and two sequences $\{g(\omega ,{\zeta }_n(\omega ))\}$ and $\{g(\omega ,{\eta }_n(\omega ))\}$ in X as follows. Let ${\zeta }_0,{\eta }_0\in \mathrm{\Theta }$ be such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$. Since $F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))\in X=g(\omega \times X)$ by an appropriate Filippov measurable implicit function theorem [1, 20, 28, 29], there is ${\zeta }_1\in \mathrm{\Theta }$ such that $g(\omega ,{\zeta }_1(\omega ))=F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$. Similarly, as $F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))\in g(\omega \times X)$, there is ${\eta }_1(\omega )\in \mathrm{\Theta }$ such that $g(\omega ,{\eta }_1(\omega ))=F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$. Now $F(\omega ,({\zeta }_1(\omega ),{\eta }_1(\omega )))$ and $F(\omega ,({\eta }_1(\omega ),{\zeta }_1(\omega )))$ are well defined. Again from $F(\omega ,({\zeta }_1(\omega ),{\eta }_1(\omega ))),F(\omega ,({\eta }_1(\omega ),{\zeta }_1(\omega )))\in g(\omega \times X)$, there are ${\zeta }_2,{\eta }_2\in \mathrm{\Theta }$ such that $g(\omega ,{\zeta }_2(\omega ))=F(\omega ,({\zeta }_1(\omega ),{\eta }_1(\omega )))$ and $g(\omega ,{\eta }_2(\omega ))=F(\omega ,({\eta }_1(\omega ),{\zeta }_1(\omega )))$. Continuing this process, we can construct sequences $\{{\zeta }_n(\omega )\}$ and $\{{\eta }_n(\omega )\}$ in X such that

$$\begin{array}{r}g(\omega ,{\zeta }_{n+1}(\omega ))=F(\omega ,({\zeta }_n(\omega ),{\eta }_n(\omega )))\text{and }\\ g(\omega ,{\eta }_{n+1}(\omega ))=F(\omega ,({\eta }_n(\omega ),{\zeta }_n(\omega )))\end{array}$$

(4)

for all $n\ge 0$.

We shall prove that

$$g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1}(\omega ))\text{for all }n\ge 0$$

(5)

and

$$g(\omega ,{\eta }_n(\omega ))\ge g(\omega ,{\eta }_{n+1}(\omega ))\text{for all }n\ge 0.$$

(6)

The proof will be given by mathematical induction. Let $n=0$. By assumption we have $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$. Since $g(\omega ,{\zeta }_1(\omega ))=F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_1(\omega ))=F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$, we have

$$g(\omega ,{\zeta }_0(\omega ))\le g(\omega ,{\zeta }_1(\omega ))\text{and}g(\omega ,{\eta }_0(\omega ))\ge g(\omega ,{\eta }_1(\omega )).$$

Therefore, (5) and (6) hold for $n=0$.

Suppose now that (5) and (6) hold for some fixed $n\ge 0$. Then, since $g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1}(\omega ))$ and $g(\omega ,{\eta }_n(\omega ))\ge g(\omega ,{\eta }_{n+1}(\omega ))$ and as F is monotone g-non-decreasing in its first argument, from (2) and (4), we have

$$\begin{array}{r}F(\omega ,({\zeta }_n(\omega ),{\eta }_n(\omega )))\le F(\omega ,({\zeta }_{n_{+1}}(\omega ),{\eta }_n(\omega )))\text{and}\\ F(\omega ,({\eta }_{n+1}(\omega ),{\zeta }_n(\omega )))\le F(\omega ,({\eta }_n(\omega ),{\zeta }_n(\omega ))).\end{array}$$

(7)

Similarly, from (3) and (4), as $g(\omega ,{\eta }_{n+1}(\omega ))\le g(\omega ,{\eta }_n(\omega ))$ and $g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1}(\omega ))$,

$$\begin{array}{r}F(\omega ,({\zeta }_{n+1}(\omega ),{\eta }_{n+1}(\omega )))\ge F(\omega ,({\zeta }_{n_{+1}}(\omega ),{\eta }_n(\omega )))\text{and}\\ F(\omega ,({\eta }_{n+1}(\omega ),{\zeta }_n(\omega )))\ge F(\omega ,({\eta }_{n+1}(\omega ),{\zeta }_{n+1}(\omega ))).\end{array}$$

(8)

Now from (7), (8), and (4), we get

$$g(\omega ,{\zeta }_{n+1}(\omega ))\le g(\omega ,{\zeta }_{n+2}(\omega ))$$

(9)

and

$$g(\omega ,{\eta }_{n+1}(\omega ))\ge g(\omega ,{\eta }_{n+2}(\omega )).$$

(10)

Thus, by mathematical induction we conclude that (5) and (6) hold for all $n\ge 0$.

Denote for each $\omega \in \mathrm{\Omega }$

$${\delta }_n=d(g(\omega ,{\zeta }_n(\omega )),g(\omega ,{\zeta }_{n+1}(\omega )))+d(g(\omega ,{\eta }_n(\omega )),g(\omega ,{\eta }_{n+1}(\omega ))).$$

We show that

$$\frac{{\delta }_n}{2}\le \phi \left(\frac{{\delta }_{n-1}}{2}\right)\text{for all }n\ge 1.$$

(11)

Since from (5) and (6) we have $g(\omega ,{\zeta }_{n-1}(\omega ))\le g(\omega ,{\zeta }_n(\omega ))$ and $g(\omega ,{\eta }_{n-1}(\omega ))\ge g(\omega ,{\eta }_n(\omega ))$, therefore from (4) and (1), we get

(12)

Similarly, from (4) and (1), as $g(\omega ,{\eta }_n(\omega ))\le g(\omega ,{\eta }_{n-1}(\omega ))$ and $g(\omega ,{\zeta }_n(\omega ))\ge g(\omega ,{\zeta }_{n-1}(\omega ))$,

(13)

By adding (12) and (13), and dividing by 2, we obtain (11).

From (11), since $\phi (t)<t$ for $t>0$, it follows that $\{{\delta }_n\}$ is the monotone decreasing sequence of positive reals. Therefore, there is some $\delta \ge 0$ such that

$$\underset{n\to \mathrm{\infty }}{lim}{\delta }_n=\delta +.$$

We show that $\delta =0$. Suppose, to the contrary, that $\delta >0$. Taking the limit in (11) when ${\delta }_n\to \delta +$ and having in mind that we assume that ${lim}_{r\to t+}\phi (t)<t$ for all $t>0$, we have

$$\frac{\delta }{2}=\underset{n\to \mathrm{\infty }}{lim}\frac{{\delta }_n}{2}\le \underset{n\to \mathrm{\infty }}{lim}\phi \left(\frac{{\delta }_{n-1}}{2}\right)=\underset{{\delta }_{n-1}\to \delta +}{lim}\phi \left(\frac{{\delta }_{n-1}}{2}\right)<\frac{\delta }{2}\text{,}$$

a contradiction. Thus, $\delta =0$.

Now we prove that for each $\omega \in \mathrm{\Omega }$, $\{g(\omega ,{\zeta }_n(\omega ))\}$ and $\{g(\omega ,{\eta }_n(\omega ))\}$ are Cauchy sequences. Suppose, to the contrary, that at least one, $\{g(\omega ,{\zeta }_n(\omega ))\}$ or $\{g(\omega ,{\eta }_n(\omega ))\}$, is not a Cauchy sequence. Then there exist an $ϵ\ge 0$ and two subsequences of positive integers $\{l(k)\}$, $\{m(k)\}$, $m(k)>l(k)\ge k$ with

$$\begin{array}{rcl}{r}_k& =& d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ \ge & ϵ\end{array}$$

(14)

for $k\in \{1,2,\dots \}$.

We may also assume

$$d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{m(k)-1}(\omega )))+d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{m(k)-1}(\omega )))<ϵ.$$

(15)

By choosing $m(k)$ to be the smallest number exceeding $l(k)$ for which (14) holds, such $m(k)$ for which (15) holds exists, because ${\delta }_n\to 0$. From (14), (15) and by the triangle inequality, we have

$$\begin{array}{rcl}ϵ& \le & r_k\\ \le & d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{m(k)-1}(\omega )))\\ +d(g(\omega ,{\zeta }_{m(k)-1}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))\\ +d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{m(k)-1}(\omega )))\\ +d(g(\omega ,{\eta }_{m(k)-1}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ =& d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{m(k)-1}(\omega )))\\ +d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{m(k)-1}(\omega )))+{\delta }_{m(k)-1}\\ <& ϵ+{\delta }_{m(k)-1}.\end{array}$$

Taking the limit as $k\to \mathrm{\infty }$, we get

$$\underset{k\to \mathrm{\infty }}{lim}{r}_k=ϵ+.$$

(16)

Inequality (14) and the triangle inequality imply now

$$\begin{array}{rcl}{r}_k& =& d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ \le & d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{l(k)+1}(\omega )))+d(g(\omega ,{\zeta }_{l(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)+1}(\omega )))\\ +d(g(\omega ,{\zeta }_{m(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{l(k)+1}(\omega )))\\ +d(g(\omega ,{\eta }_{l(k)+1}(\omega )),g(\omega ,{\eta }_{m(k)+1}(\omega )))+d(g(\omega ,{\eta }_{m(k)+1}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ =& d(g(\omega ,{\zeta }_{l(k)}(\omega )),g(\omega ,{\zeta }_{l(k)+1}(\omega )))+d(g(\omega ,{\eta }_{l(k)}(\omega )),g(\omega ,{\eta }_{l(k)+1}(\omega )))\\ +[d(g(\omega ,{\zeta }_{m(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{m(k)}(\omega )),g(\omega ,{\eta }_{m(k)+1}(\omega )))]\\ +d(g(\omega ,{\zeta }_{l(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)+1}(\omega )))+d(g(\omega ,{\eta }_{l(k)+1}(\omega )),g(\omega ,{\eta }_{m(k)+1}(\omega ))).\end{array}$$

Hence,

$$\begin{array}{rcl}{r}_k& \le & {\delta }_{l(k)}+{\delta }_{m(k)}+d(g(\omega ,{\zeta }_{l(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)+1}(\omega )))\\ +d(g(\omega ,{\eta }_{l(k)+1}(\omega )),g(\omega ,{\eta }_{m(k)+1}(\omega ))).\end{array}$$

(17)

From (5) and (6), we conclude that $g(\omega ,{\zeta }_{l(k)}(\omega ))\le g(\omega ,{\zeta }_{m(k)}(\omega ))$ and $g(\omega ,{\eta }_{l(k)}(\omega ))\ge g(\omega ,{\eta }_{m(k)}(\omega ))$.

Now (1) and (4) imply that

(18)

Also, from (1) and (4), as $g(\omega ,{\eta }_{m(k)}(\omega ))\le g(\omega ,{\eta }_{l(k)}(\omega ))$ and $g(\omega ,{\zeta }_{m(k)}(\omega ))\ge g(\omega ,{\zeta }_{l(k)}(\omega ))$,

(19)

Inserting (18) and (19) in (17), we obtain

$$r_k\le {\delta }_{l(k)}+{\delta }_{m(k)}+2\phi \left(\frac{r_k}{2}\right).$$

Letting $k\to \mathrm{\infty }$, we get by (16)

$$ϵ\le 2\underset{k\to \mathrm{\infty }}{lim}\phi \left(\frac{r_k}{2}\right)=2\underset{r_k\to ϵ+}{lim}\phi \left(\frac{r_k}{2}\right)<2\frac{ϵ}{2}=ϵ,$$

(20)

a contradiction. Therefore, our supposition (14) was wrong. Thus, we proved that $\{g(\omega ,{\zeta }_n(\omega ))\}$ and $\{g(\omega ,{\eta }_n(\omega ))\}$ are Cauchy sequences in X.

Since X is complete and $g(\omega \times X)=X$, there exist ${\zeta }_0,{\theta }_0\in \mathrm{\Theta }$ such that ${lim}_{n\to \mathrm{\infty }}g(\omega ,{\zeta }_n(\omega ))=g(\omega ,{\zeta }_0(\omega ))$ and ${lim}_{n\to \mathrm{\infty }}g(\omega ,{\eta }_n(\omega ))=g(\omega ,{\theta }_0(\omega ))$. Since $g(\omega ,{\zeta }_0(\omega ))$ and $g(\omega ,{\theta }_0(\omega ))$ are measurable, therefore the functions $\zeta (\omega )$ and $\theta (\omega )$, defined by $\zeta (\omega )=g(\omega ,{\zeta }_0(\omega ))$ and $\theta (\omega )=g(\omega ,{\theta }_0(\omega ))$ are measurable. Thus,

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}F(\omega ,({\zeta }_n(\omega ),{\eta }_n(\omega )))=\underset{n\to \mathrm{\infty }}{lim}g(\omega ,{\zeta }_n(\omega ))=\zeta (\omega )\text{and}\\ \underset{n\to \mathrm{\infty }}{lim}F(\omega ,({\eta }_n(\omega ),{\zeta }_n(\omega )))=\underset{n\to \mathrm{\infty }}{lim}g(\omega ,{\eta }_n(\omega ))=\theta (\omega ).\end{array}$$

(21)

Since F and g are compatible mappings, we have by (21)

(22)

(23)

Next, we prove that

$$g(\omega ,\zeta (\omega ))=F(\omega ,(\zeta (\omega ),\theta (\omega )))$$

and

$$g(\omega ,\theta (\omega ))=F(\omega ,(\theta (\omega ),\zeta (\omega ))).$$

Let (a) hold. We have

Taking the limit as $n\to \mathrm{\infty }$, using (4), (21), and (22) and the fact that F and g are continuous, we have

$$d(g(\omega ,\zeta (\omega )),F(\omega ,(\zeta (\omega ),\theta (\omega ))))=0.$$

Similarly, from (4), (21), and (23) and the continuity of F and g, we have

$$d(g(\omega ,\theta (\omega )),F(\omega ,(\theta (\omega ),\zeta (\omega ))))=0.$$

Combining the above two results, we obtain

$$g(\omega ,\zeta (\omega ))=F(\omega ,(\zeta (\omega ),\theta (\omega )))$$

and

$$g(\omega ,\theta (\omega ))=F(\omega ,(\theta (\omega ),\zeta (\omega )))$$

for each $\omega \in \mathrm{\Omega }$.

Next, suppose that (b) holds. From (5), (6), and (21), we have $\{g(\omega ,{\zeta }_n(\omega ))\}$ is non-decreasing and $\{g(\omega ,{\eta }_n(\omega ))\}$ is non-increasing sequence and

$$g(\omega ,{\zeta }_n(\omega ))\to g(\omega ,\zeta (\omega )),g(\omega ,{\eta }_n(\omega ))\to g(\omega ,\theta (\omega ))\text{.}$$

So, from (2) and (3), we have for all $n\ge 0$

$$g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,\zeta (\omega ))\text{and}g(\omega ,{\eta }_n(\omega ))\ge g(\omega ,\theta (\omega )).$$

(24)

Since F and g are compatible mappings and g is continuous, by (22) and (23) we have

(25)

and

(26)

Now, we have

Taking the limit as $n\to \mathrm{\infty }$ in the above inequality, using (4) and (25), we have

Since the mapping g is monotone increasing, by (1), (24), and the above inequality, we have for all $n\ge 0$

Using (21) and the property of a φ-function, we obtain

$$d(g(\omega ,\zeta (\omega )),F(\omega ,(\zeta (\omega ),\theta (\omega ))))\le 0.$$

That is,

$$g(\omega ,\zeta (\omega ))=F(\omega ,(\zeta (\omega ),\theta (\omega ))).$$

And similarly, by the virtue of (4), (21), and (26), we obtain

$$g(\omega ,\theta (\omega ))=F(\omega ,(\theta (\omega ),\zeta (\omega ))).$$

This proves that F and g have a coupled random coincidence point. □

Corollary 3.3 Let $(X,\le ,d)$ be a complete separable partially ordered metric space, $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space, and $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ be mappings such that

• (i) $g(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$;

• (ii) $F(\cdot ,v)$, $g(\cdot ,x)$ are measurable for all $v\in X\times X$ and $x\in X$ respectively;

• (iii) $F(\omega ,\cdot )$ has the mixed $g(\omega ,\cdot )$-monotone property for each $\omega \in \mathrm{\Omega }$ and for some $k\in [0,1)$

  $$d(F(\omega ,(x,y)),F(\omega ,(u,v)))\le \frac{k}{2}(d(g(\omega ,x),g(\omega ,u))+d(g(\omega ,y),g(\omega ,v)))$$

for all $x,y,u,v\in X$, for which $g(\omega ,x)\le g(\omega ,u)$ and $g(\omega ,y)\ge g(\omega ,v)$ for all $\omega \in \mathrm{\Omega }$.

Suppose $g(\omega \times X)=X$ for each $\omega \in \mathrm{\Omega }$, g is monotone increasing, and F and g are compatible random operators. Also suppose either

• (a) $F(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$ or

• (b) X has the following property:

• (i) if a non-decreasing sequence $\{x_n\}\to x$, then $x_n\le x$ for all n,

• (ii) if a non-increasing sequence $\{y_n\}\to y$, then $y_n\ge y$ for all n.

If there exist measurable mappings ${\zeta }_0,{\eta }_0:\mathrm{\Omega }\to X$ such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$, then there are measurable mappings $\zeta ,\theta :\mathrm{\Omega }\to X$ such that $F(\omega ,(\zeta (\omega ),\theta (\omega )))=g(\omega ,\zeta (\omega ))$ and $F(\omega ,(\theta (\omega ),\zeta (\omega )))=g(\omega ,\theta (\omega ))$ for all $\omega \in \mathrm{\Omega }$, that is, F and g have a coupled random coincidence point.

Proof Taking $\varphi (t)=k\cdot t$ with $k\in [0,1)$ in Theorem 3.2, we obtain the result. □

The following theorem presents the stochastic version of Theorem 2.7 and generalizes the recent results in [20].

Theorem 3.4 Let $(X,\le ,d)$ be a complete separable partially ordered metric space, $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space, and $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ be mappings such that

• (i) $g(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$;

• (ii) $F(\cdot ,v)$, $g(\cdot ,x)$ are measurable for all $v\in X\times X$ and $x\in X$, respectively;

• (iii) $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ are such that $F(\omega ,\cdot )$ has the mixed $g(\omega ,\cdot )$-monotone property for each $\omega \in \mathrm{\Omega }$; and suppose there exist $\varphi \in \mathrm{\Phi }$ and $\psi \in \mathrm{\Psi }$, satisfying conditions of Theorem  2.7, such that

  

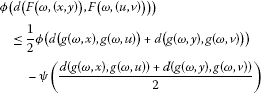  (27)

for all $x,y,u,v\in X$, for which $g(\omega ,x)\le g(\omega ,u)$ and $g(\omega ,y)\ge g(\omega ,v)$ for all $\omega \in \mathrm{\Omega }$.

Suppose $g(\omega \times X)=X$ for each $\omega \in \mathrm{\Omega }$, g is monotone increasing, and F and g are compatible random operators. Also suppose either

• (a) $F(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$ or

• (b) X has the following property:

  

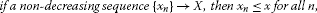  (28)
  

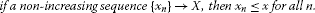  (29)

If there exist measurable mappings ${\zeta }_0,{\eta }_0:\mathrm{\Omega }\to X$ such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$, then there are measurable mappings $\zeta ,\theta :\mathrm{\Omega }\to X$ such that $F(\omega ,(\zeta (\omega ),\theta (\omega )))=g(\omega ,\zeta (\omega ))$ and $F(\omega ,(\theta (\omega ),\zeta (\omega )))=g(\omega ,\theta (\omega ))$ for all $\omega \in \mathrm{\Omega }$, that is, F and g have a coupled random coincidence.

Proof Let $\ominus =\{\zeta :\mathrm{\Omega }\to X\}$ be a family of measurable mappings. Define a function $h:\mathrm{\Omega }\times X\to R^{+}$ as follows:

$$h(\omega ,x)=d(x,g(\omega ,x)).$$

Since $X\to g(\omega ,x)$ is continuous for all $\omega \in \mathrm{\Omega }$, we conclude that $h(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$. Also, since $x\to g(\omega ,x)$ is measurable for all $x\in X$, we conclude that $h(\cdot ,x)$ is measurable for all $\omega \in \mathrm{\Omega }$ (see [26], p.868). Thus, $h(\omega ,x)$ is the Caratheodory function. Therefore, if $\zeta :\mathrm{\Omega }\to X$ is a measurable mapping, then $\omega \to h(\omega ,\zeta (\omega ))$ is also measurable (see [27]). Also, for each $\zeta \in \ominus$, the function $\eta :\mathrm{\Omega }\to X$ defined by $\eta (\omega )=g(\omega ,\zeta (\omega ))$ is measurable, that is, $\eta \in \ominus$. Now, we shall construct two sequences of measurable mappings $\{{\zeta }_n\}$ and $\{{\eta }_n\}$ in ⊖, and two sequences $\{g(\omega ,{\zeta }_n(\omega ))\}$ and $\{g(\omega ,{\eta }_n(\omega ))\}$ in X as follows. Let ${\zeta }_0,{\eta }_0\in \ominus$ such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$. Since $F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))\in X=g(\omega \times X)$, by an appropriate Filippov measurable implicit function theorem [1, 20, 28, 29], there is ${\zeta }_1\in \ominus$ such that $g(\omega ,{\zeta }_1(\omega ))=F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$. Similarly, as $F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))\in X=g(\omega \times X)$, there is ${\eta }_1(\omega )\in \ominus$ such that $g(\omega ,{\eta }_1(\omega ))=F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$. Now, $F(\omega ,({\zeta }_1(\omega ),{\eta }_1(\omega )))$ and $F(\omega ,({\eta }_1(\omega ),{\zeta }_1(\omega )))$ are well defined. Again, from $F(\omega ,({\zeta }_1(\omega ),{\eta }_1(\omega ))),F(\omega ,({\eta }_1(\omega ),{\zeta }_1(\omega )))\in g(\omega \times X)$, there are ${\zeta }_2,{\eta }_2\in \ominus$ such that $g(\omega ,{\zeta }_2(\omega ))=F(\omega ,({\zeta }_1(\omega ),{\eta }_1(\omega )))$ and $g(\omega ,{\eta }_2(\omega ))=F(\omega ,({\eta }_1(\omega ),{\zeta }_1(\omega )))$. Continuing this process, we can construct sequences $\{{\zeta }_n(\omega )\}$ and $\{{\eta }_n(\omega )\}$ in X such that

$$\begin{array}{r}g(\omega ,{\zeta }_{n+1}(\omega ))=F(\omega ,({\zeta }_n(\omega ),{\eta }_n(\omega )))\text{and }\\ g(\omega ,{\eta }_{n+1}(\omega ))=F(\omega ,{\eta }_n(\omega ),{\zeta }_n(\omega ))\end{array}$$

(30)

for all $n\ge 0$.

We shall prove that

$$g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1}(\omega ))\text{for all }n\ge 0$$

(31)

and

$$g(\omega ,{\eta }_n(\omega ))\le g(\omega ,{\eta }_{n+1}(\omega ))\text{for all }n\ge 0.$$

(32)

The proof will be given by mathematical induction. Let $n=0$. By assumption, we have $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$. Since $g(\omega ,{\zeta }_1(\omega ))=F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_1(\omega ))=F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$, we have $g(\omega ,{\zeta }_0(\omega ))\le g(\omega ,{\zeta }_1(\omega ))$ and $g(\omega ,{\eta }_0(\omega ))\ge g(\omega ,{\eta }_1(\omega ))$. Therefore, (31) and (32) hold for $n=0$. Suppose now that (31) and (32) hold for some fixed $n\ge 0$. Then $g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1}(\omega ))$ and $g(\omega ,{\eta }_n(\omega ))\ge g(\omega ,{\eta }_{n+1}(\omega ))$ as F is monotone g-non-decreasing in its first argument, from (28) and (30),

$$\begin{array}{r}F(\omega ,({\zeta }_n(\omega ),{\eta }_n(\omega )))\le F(\omega ,({\zeta }_{n+1}(\omega ),{\eta }_n(\omega )))\text{and}\\ F(\omega ,({\eta }_{n+1}(\omega ),{\zeta }_n(\omega )))\le F(\omega ,({\eta }_n(\omega ),{\zeta }_n(\omega ))).\end{array}$$

(33)

Similarly, from (29) and (30), as $g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1}(\omega ))$ and $g(\omega ,{\eta }_n(\omega ))\ge g(\omega ,{\eta }_{n+1}(\omega ))$, we have

$$\begin{array}{r}F(\omega ,({\zeta }_{n+1}(\omega ),{\eta }_{n+1}(\omega )))\ge F(\omega ,({\zeta }_{n+1}(\omega ),{\eta }_n(\omega )))\text{and}\\ F(\omega ,({\eta }_{n+1}(\omega ),{\zeta }_n(\omega )))\ge F(\omega ,({\eta }_{n+1}(\omega ),{\zeta }_{n+1}(\omega ))).\end{array}$$

(34)

Now, from (30), (33), and (34), we get

$$g(\omega ,{\zeta }_{n+1}(\omega ))\le g(\omega ,{\zeta }_{n+2}(\omega ))$$

(35)

and

$$g(\omega ,{\eta }_{n+1}(\omega ))\le g(\omega ,{\eta }_{n+2}(\omega )).$$

(36)

Thus, by mathematical induction we conclude that (31) and (32) hold for all $n\ge 0$.

Therefore,

$$g(\omega ,{\zeta }_0(\omega ))\le g(\omega ,{\zeta }_1(\omega ))\le \cdots \le g(\omega ,{\zeta }_n(\omega ))\le g(\omega ,{\zeta }_{n+1})\le \cdots$$

(37)

and

$$g(\omega ,{\eta }_0(\omega ))\ge g(\omega ,{\eta }_1(\omega ))\ge \cdots \ge g(\omega ,{\eta }_n(\omega ))\ge \cdots \ge g(\omega ,{\eta }_{n+1})\ge \cdots .$$

(38)

Since $g(\omega ,{\zeta }_{n-1}(\omega ))\le g(\omega ,{\zeta }_n(\omega ))$ and $g(\omega ,{\eta }_n(\omega ))\le g(\omega ,{\eta }_{n-1}(\omega ))$, using (27) and (30), we have

(39)

Similarly, since $g(\omega ,{\zeta }_{n-1}(\omega ))\le g(\omega ,{\zeta }_n(\omega ))$ and $g(\omega ,{\eta }_{n-1}(\omega ))\le g(\omega ,{\eta }_n(\omega ))$, using (27) and (30), we also have

(40)

Using (39) and (40), we have

(41)

From the property (iii) of ϕ, we have

(42)

Using (41) and (42), we have

(43)

Since ψ is a non-negative function, therefore we have

Using the fact that ϕ is non-decreasing, we get

Let

$${\delta }_n=d(g(\omega ,{\zeta }_{n+1}(\omega )),g(\omega ,{\zeta }_n(\omega )))+d(g(\omega ,{\eta }_{n+1}(\omega )),g(\omega ,{\eta }_n(\omega ))).$$

Now, we show that ${\delta }_n\to 0$ as $n\to \mathrm{\infty }$. It is clear that the sequence $\{{\delta }_n\}$is decreasing; therefore, there is some $\delta \ge 0$ such that

$$\begin{array}{rcl}\underset{n\to \mathrm{\infty }}{lim}{\delta }_n& =& \underset{n\to \mathrm{\infty }}{lim}[d(g(\omega ,{\zeta }_{n+1}(\omega )),g(\omega ,{\zeta }_n(\omega )))+d(g(\omega ,{\eta }_{n+1}(\omega )),g(\omega ,{\eta }_n(\omega )))]\\ =& \delta .\end{array}$$

(44)

We shall show that $\delta =0$. Suppose, to the contrary, that $\delta >0$. Then taking the limit as $n\to \mathrm{\infty }$ on both sides of (43) and as ${lim}_{t\to r}\psi (t)>0$ for all $r>0$ and ϕ is continuous, we have

$$\begin{array}{rcl}\varphi (\delta )& =& \underset{n\to \mathrm{\infty }}{lim}\varphi ({\delta }_n)\le \underset{n\to \mathrm{\infty }}{lim}[\varphi ({\delta }_{n-1})-2\psi \left(\frac{{\delta }_{n-1}}{2}\right)]\\ =& \varphi (\delta )-2\underset{{\delta }_{n-1}\to \delta }{lim}\psi \left(\frac{{\delta }_{n-1}}{2}\right)<\varphi (\delta ),\end{array}$$

a contradiction. Thus, $\delta =0$, that is

$$\begin{array}{rcl}\underset{n\to \mathrm{\infty }}{lim}{\delta }_n& =& \underset{n\to \mathrm{\infty }}{lim}[d(g(\omega ,{\zeta }_{n+1}(\omega )),g(\omega ,{\zeta }_n(\omega )))+d(g(\omega ,{\eta }_{n+1}(\omega )),g(\omega ,{\eta }_n(\omega )))]\\ =& 0.\end{array}$$

(45)

Now, we will prove that $\{g(\omega ,{\zeta }_n)\}$, $\{g(\omega ,{\eta }_n)\}$ are Cauchy sequences. Suppose, to the contrary, that at least one of $\{g(\omega ,{\zeta }_n)\}$ or $\{g(\omega ,{\eta }_n)\}$ is not a Cauchy sequence. Then there exists an $ϵ>0$ for which we can find subsequences of positive integers $\{m_k\}$, $\{n_k\}$ with $n(k)>m(k)\ge k$ such that

$$\begin{array}{rcl}{r}_k& :=& d(g(\omega ,{\zeta }_{n(k)}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{n(k)}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ \ge & ϵ\end{array}$$

(46)

for $k=\{1,2,3,\dots \}$. We may also assume

$$d(g(\omega ,{\zeta }_{n(k)-1}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{n(k)-1}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))<ϵ$$

(47)

by choosing $n(k)$ in such a way that it is the smallest integer with $n(k)>m(k)$ and satisfying (46). Using (46), (47), and the triangle inequality, we have

$$\begin{array}{rcl}ϵ& \le & r_k:=d(g(\omega ,{\zeta }_{n(k)}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{n(k)}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ \le & d(g(\omega ,{\zeta }_{n(k)}(\omega )),g(\omega ,{\zeta }_{n(k)-1}(\omega )))+d(g(\omega ,{\zeta }_{n(k)-1}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))\\ +d(g(\omega ,{\eta }_{n(k)}(\omega )),g(\omega ,{\eta }_{n(k)-1}(\omega )))+d(g(\omega ,{\eta }_{n(k)-1}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ \le & d(g(\omega ,{\zeta }_{n(k)}(\omega )),g(\omega ,{\zeta }_{n(k)-1}(\omega )))+d(g(\omega ,{\eta }_{n(k)}(\omega )),g(\omega ,{\eta }_{n(k)-1}(\omega )))\\ +d(g(\omega ,{\zeta }_{n(k)-1}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{n(k)-1}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))\\ \le & d(g(\omega ,{\zeta }_{n(k)}(\omega )),g(\omega ,{\zeta }_{n(k)-1}(\omega )))+d(g(\omega ,{\eta }_{n(k)}(\omega )),g(\omega ,{\eta }_{n(k)-1}(\omega )))+ϵ.\end{array}$$

Letting $k\to \mathrm{\infty }$ and using (45), we get

$$\begin{array}{rcl}\underset{k\to \mathrm{\infty }}{lim}{r}_k& =& \underset{k\to \mathrm{\infty }}{lim}[d(g(\omega ,{\zeta }_{n(k)}(\omega )),g(\omega ,{\zeta }_{m(k)}(\omega )))+d(g(\omega ,{\eta }_{n(k)}(\omega )),g(\omega ,{\eta }_{m(k)}(\omega )))]\\ =& ϵ.\end{array}$$

(48)

By the triangle inequality,

(49)

Using the property of ϕ, we have

$$\begin{array}{rcl}\varphi (r_k)& =& \varphi ({\delta }_{n(k)}+{\delta }_{m(k)}+d(g(\omega ,{\zeta }_{n(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)+1}(\omega )))\\ +d(g(\omega ,{\eta }_{n(k)+1}(\omega )),g(\omega ,{\eta }_{m(k)+1}(\omega ))))\\ \le & \varphi ({\delta }_{n(k)}+{\delta }_{m(k)})+\varphi \left(d(g(\omega ,{\zeta }_{n(k)+1}(\omega )),g(\omega ,{\zeta }_{m(k)+1}(\omega )))\right)\\ +\varphi \left(d(g(\omega ,{\eta }_{n(k)+1}(\omega )),g(\omega ,{\eta }_{m(k)+1}(\omega )))\right).\end{array}$$

Since $n(k)>m(k)$, hence $g(\omega ,{\zeta }_{n(k)}(\omega ))\ge g(\omega ,{\zeta }_{m(k)}(\omega ))$ and $g(\omega ,{\eta }_{n(k)}(\omega ))\le g(\omega ,{\eta }_{m(k)}(\omega ))$. Using (27) and (30), we get

(50)

By the same way, we also have

(51)

Putting (50) and (51) in (49), we have

$$\begin{array}{rcl}\varphi (r_k)& \le & \varphi ({\delta }_{n(k)}+{\delta }_{m(k)})+\frac{1}{2}\varphi (r_k)-\psi \left(\frac{r_k}{2}\right)+\frac{1}{2}\varphi (r_k)-\psi \left(\frac{r_k}{2}\right)\\ =& \varphi ({\delta }_{n(k)}+{\delta }_{m(k)})+\varphi (r_k)-2\psi \left(\frac{r_k}{2}\right).\end{array}$$

Taking $k\to \mathrm{\infty }$ and using (45) and (48), we get

$$\begin{array}{rcl}\varphi (ϵ)& \le & \varphi (0)+\varphi (ϵ)-2\underset{k\to \mathrm{\infty }}{lim}\psi \left(\frac{r_k}{2}\right)\\ =& \varphi (ϵ)-2\underset{r_k\to ϵ}{lim}\psi \left(\frac{r_k}{2}\right)<\varphi (ϵ),\end{array}$$

a contradiction. This shows that $\{g(\omega ,{\zeta }_n)\}$ and $\{g(\omega ,{\eta }_n)\}$ are Cauchy sequences.

Since X is complete and $g(\omega \times X)=X$, there exist ${\zeta }_0,{\theta }_0\in \mathrm{\Theta }$ such that ${lim}_{n\to \mathrm{\infty }}g(\omega ,{\zeta }_n(\omega ))=g(\omega ,{\zeta }_0(\omega ))$ and ${lim}_{n\to \mathrm{\infty }}g(\omega ,{\eta }_n(\omega ))=g(\omega ,{\theta }_0(\omega ))$. Since $g(\omega ,{\zeta }_0(\omega ))$ and $g(\omega ,{\theta }_0(\omega ))$ are measurable, then the functions $\zeta (\omega )$ and $\theta (\omega )$, defined by $\zeta (\omega )=g(\omega ,{\zeta }_0(\omega ))$ and $\theta (\omega )=g(\omega ,{\theta }_0(\omega ))$, are measurable. Thus,

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}F(\omega ,({\zeta }_n(\omega ),{\eta }_n(\omega )))=\underset{n\to \mathrm{\infty }}{lim}g(\omega ,{\zeta }_n(\omega ))=\zeta (\omega )\text{and}\\ \underset{n\to \mathrm{\infty }}{lim}F(\omega ,({\eta }_n(\omega ),{\zeta }_n(\omega )))=\underset{n\to \mathrm{\infty }}{lim}g(\omega ,{\eta }_n(\omega ))=\theta (\omega ).\end{array}$$

(52)

Using the compatibility of F and g and the technique of the proof of Theorem 3.2, we obtain the required conclusion. □

Corollary 3.5 Let $(X,\le ,d)$ be a complete separable partially ordered metric space, $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space, and $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ be mappings such that

• (i) $g(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$;

• (ii) $F(\cdot ,v)$, $g(\cdot ,x)$ are measurable for all $v\in X\times X$ and $x\in X$ respectively;

• (iii) $F(\omega ,\cdot )$ has the mixed $g(\omega ,\cdot )$-monotone property for each $\omega \in \mathrm{\Omega }$; and suppose there exist $\varphi \in \mathrm{\Phi }$ and $\psi \in \mathrm{\Psi }$ such that

  $$\begin{array}{rcl}d(F(\omega ,(x,y)),F(\omega ,(u,v)))& \le & \frac{1}{2}(d(g(\omega ,x),g(\omega ,u))+d(g(\omega ,y),g(\omega ,v)))\\ -\psi \left(\frac{d(g(\omega ,x),g(\omega ,u))+d(g(\omega ,y),g(\omega ,v))}{2}\right)\end{array}$$

for all $x,y,u,v\in X$, for which $g(\omega ,x)\le g(\omega ,u)$ and $g(\omega ,y)\ge g(\omega ,v)$ for all $\omega \in \mathrm{\Omega }$.

Suppose $g(\omega \times X)=X$ for each $\omega \in \mathrm{\Omega }$, g is continuous and monotone increasing, and F and g are compatible mappings. Also suppose either

• (a) $F(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$ or

• (b) X has the following property:

• (i) if a non-decreasing sequence $\{x_n\}\to X$, then $x_n\le x$ for all n,

• (ii) if a non-increasing sequence $\{x_n\}\to X$, then $x_n\le x$ for all n.

If there exist measurable mappings ${\zeta }_0,{\eta }_0:\mathrm{\Omega }\to X$ such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$, then there are measurable mappings $\zeta ,\theta :\mathrm{\Omega }\to X$ such that $F(\omega ,(\zeta (\omega ),\theta (\omega )))=g(\omega ,\zeta (\omega ))$ and $F(\omega ,(\theta (\omega ),\zeta (\omega )))=g(\omega ,\theta (\omega ))$ for all $\omega \in \mathrm{\Omega }$, that is, F and g have a coupled random coincidence.

Proof Take $\varphi (t)=t$ in Theorem 3.4. □

Corollary 3.6 Let $(X,\le ,d)$ be a complete separable partially ordered metric space, $(\mathrm{\Omega },\mathrm{\Sigma })$ be a measurable space, and $F:\mathrm{\Omega }\times (X\times X)\to X$ and $g:\mathrm{\Omega }\times X\to X$ be mappings such that

• (i) $g(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$;

• (ii) $F(\cdot ,v)$, $g(\cdot ,x)$ are measurable for all $v\in X\times X$ and $x\in X$ respectively;

• (iii) $F(\omega ,\cdot )$ has the mixed $g(\omega ,\cdot )$-monotone property for each $\omega \in \mathrm{\Omega }$; and suppose there exists $k\in [0,1)$ such that

  $$\left(d(F(\omega ,(x,y)),F(\omega ,(u,v)))\right)\le \frac{k}{2}(d(g(\omega ,x),g(\omega ,u))+d(g(\omega ,y),g(\omega ,v)))$$

for all $x,y,u,v\in X$, for which $g(\omega ,x)\le g(\omega ,u)$ and $g(\omega ,y)\ge g(\omega ,v)$ for all $\omega \in \mathrm{\Omega }$.

Suppose $g(\omega \times X)=X$ for each $\omega \in \mathrm{\Omega }$, g is monotone increasing, and F and g are compatible random operators. Also suppose either

• (a) $F(\omega ,\cdot )$ is continuous for all $\omega \in \mathrm{\Omega }$ or

• (b) X has the following property:

• (i) if a non-decreasing sequence $\{x_n\}\to X$, then $x_n\le x$ for all n,

• (ii) if a non-increasing sequence $\{x_n\}\to X$, then $x_n\le x$ for all n.

If there exist measurable mappings ${\zeta }_0,{\eta }_0:\mathrm{\Omega }\to X$ such that $g(\omega ,{\zeta }_0(\omega ))\le F(\omega ,({\zeta }_0(\omega ),{\eta }_0(\omega )))$ and $g(\omega ,{\eta }_0(\omega ))\ge F(\omega ,({\eta }_0(\omega ),{\zeta }_0(\omega )))$ for all $\omega \in \mathrm{\Omega }$, then there are measurable mappings $\zeta ,\theta :\mathrm{\Omega }\to X$ such that $F(\omega ,(\zeta (\omega ),\theta (\omega )))=g(\omega ,\zeta (\omega ))$ and $F(\omega ,(\theta (\omega ),\zeta (\omega )))=g(\omega ,\theta (\omega ))$ for all $\omega \in \mathrm{\Omega }$, that is, F and g have a coupled random coincidence point.

Proof Take $\psi (t)=\frac{1-k}{2}t$ in Corollary 3.5. □

Remark 3.7 By defining $g:\mathrm{\Omega }\times X\to X$ as $g(\omega ,x)=x$ for all $\omega \in \mathrm{\Omega }$ in Theorem 3.2-Corollary 3.6, we obtain corresponding coupled random fixed point results.