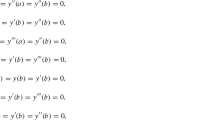Lyapunov-type inequalities for 2M th order equations under clamped-free boundary conditions

Abstract

This paper generalizes the well-known Lyapunov-type inequalities for second-order linear differential equations to certain 2M th order linear differential equations

$${(-1)}^M{u}^{(2M)}(x)-r(x)u(x)=0(-s\le x\le s)$$

under clamped-free boundary conditions. The usage of the best constant of some kind of a Sobolev inequality helps clarify the process for obtaining the result.

1 Introduction

Let us consider the second-order linear differential equation

$$\{\begin{array}{c}{u}^{″}(x)+r(x)u(x)=0(-s\le x\le s),\hfill \\ u(\pm s)=0,\hfill \end{array}$$

(1)

where . It is well known that the Lyapunov inequality

$${\int }_{-s}^s{r}^{+}(x)dx>\frac{2}{s}$$

(2)

gives a necessary condition for the existence of non-trivial classical solutions of (1), where $r^{+}(x)=(r(x)+|r(x)|)/2$. There are various extensions and applications for the above result; see, for example, surveys of Brown and Hinton [1] for relations to other fields and Tiryaki [2] for recent developments. Extensions to higher-order equations

$$\{\begin{array}{c}{u}^{(n)}(x)+r(x)u(x)=0(-s\le x\le s),\hfill \\ \text{Boundary Conditions},\hfill \end{array}$$

(3)

will be one important aspect. The first result for the high-order equation (3) is due to Levin [3], which states without proof:

Theorem A Let $n=2M$, and a non-trivial solution of (3) satisfies the clamped boundary condition, $u^{(i)}(\pm s)=0$ ($i=0,1,\dots ,M-1$). Then it holds that

$${\int }_{-s}^s{r}^{+}(x)dx>\frac{2^{2M-1}(2M-1){\{(M-1)!\}}^2}{s^{2M-1}}.$$

Later, Das and Vatsala [4] gave the proof and extended the result by constructing the Green function. Other interesting developments for higher-order equations are seen in [5–9]. For example, as shown in Yang [8], Lyapunov-type inequalities can be obtained under the following conditions:

$$\{\begin{array}{cc}(\mathrm{a})\hfill & n=2M+1,u^{(i)}(\pm s)=0(i=0,\dots ,M-1),\hfill \\ u^{(2M)}(d)=0(-s<d<s)\text{ (see also [10])}\hfill \\ (\mathrm{b})\hfill & n\ge 2,u(-s)=u(t_2)=\cdots =u(t_{n-1})=u(s)=0,\hfill \\ \text{where, }-s=t_1<t_2<\cdots <t_{n-1}<t_n=s\text{ (see also [10])}\hfill \\ (\mathrm{c})\hfill & n=2M,u^{(2i)}(\pm s)=0(i=0,\dots ,M-1)\text{ (see also [5])}\hfill \\ (\mathrm{d})\hfill & n\ge 2,u^{(i)}(-s)=0(i=0,\dots ,k-1),u^{(j)}(s)=0(j=0,\dots ,n-k-1)\hfill \\ \text{where }k\text{ runs over the range }(1\le k\le n).\hfill \end{array}$$

Here we note for the condition (c), very recently Çakmak [11], He and Tang [12], He and Zang [13] and [14] improved and extended the results of [5] and [8]. This paper considers the necessary condition for the existence of a non-trivial solution of the 2M th order linear differential equation

$${(-1)}^M{u}^{(2M)}(x)-r(x)u(x)=0(-s\le x\le s)$$

(4)

under yet another boundary condition:

Clamped-free boundary condition

$$u^{(i)}(-s)=0,u^{(M+i)}(s)=0(i=0,\dots ,M-1).$$

The main result is as follows.

Theorem 1 Suppose a non-trivial solution u of (4) exists under the clamped-free boundary condition, then it holds

$${\int }_{-s}^s{r}^{+}(x)dx>\frac{{\{(M-1)!\}}^2(2M-1)}{{(2s)}^{2M-1}}.$$

(5)

Moreover, the estimate is sharp in the sense that there exists a function $r(x)$, and for this $r(x)$, the solution u of (4) exits such that the right-hand side is arbitrarily close to the left-hand side.

The result is obtained using Takemura [[15], Theorem 1], which computes the best constant of some kind of a Sobolev inequality. In Section 4, we give a concise proof for an $L^p$ extension of Theorem 1 of [15].

2 Proof of Theorem 1

Now, let us introduce the following $L^p$-type Sobolev inequality:

$${\left(\underset{-s\le x\le s}{sup}|u^{(m)}(x)|\right)}^p\le C{\int }_{-s}^s{|u^{(M)}(x)|}^{p}dx,$$

(6)

where u belongs to

$$W(M,p):=\{u|u^{(M)}\in L^p(-s,s),u^{(i)}(-s)=0(i=0,\dots ,M-1)\},$$

$1<p$, m runs over the range $0\le m\le M-1$, and $u^{(i)}$ is the i th derivative of u in a distributional sense. We denote by $C_{CF}(M,m,p)$ the best constant of the above Sobolev inequality (6). Here, we note that in [15], Takemura obtained the best constant for $p=2$, $m=0$ by constructing the Green function of the clamped-free boundary value problem. Although, for the proof of Theorem 1, we simply need the value $C_{CF}(M,0,2)$, we would like to compute $C_{CF}(M,m,p)$ for general p and m since the proof presented in Section 4 does not depend on special values of p and m and quite simplifies the proof of Theorem 1 of [15]. Now, we have the following propositions.

Proposition 1 The best constant of (6) is

$$C_{CF}(M,m,p)=\frac{1}{{\{(M-m-1)!\}}^p}{\left(\frac{(p-1){(2s)}^{\frac{p(M-m)-1}{p-1}}}{p(M-m)-1}\right)}^{p-1},$$

(7)

and it is attained by

$$u_{\ast }(x)={\int }_{-s}^x\frac{{(x-t)}^{M-1}}{(M-1)!}\cdot {\left\{\frac{{(s-t)}^{M-1-m}}{(M-1-m)!}\right\}}^{p-1}dt.$$

(8)

Proposition 2 Suppose a $C^{2M}[-s,s]$ solution of (4) with the clamped-free boundary condition exists, then it holds that

$${\int }_{-s}^s{r}^{+}(x)dx>\frac{1}{C_{CF}(M,0,2)}.$$

(9)

Moreover, the estimate is sharp.

Proof of Theorem 1 Clearly, Theorem 1 is obtained from Propositions 1 and 2. □

Thus, all we have to do is to show Propositions 1 and 2. Before proceeding with the proof of these propositions, we would like to show a corollary obtained from Proposition 1.

Corollary 1 Suppose a non-trivial solution u of the non-linear equation

$${(-1)}^{M}u(x)u^{(2M)}(x)-r(x){(u^{(m)}(x))}^2=0$$

(10)

exists under the clamped-free boundary condition, where m satisfies ($1\le m\le M-1$), then it holds

$${\int }_{-s}^s{r}^{+}(x)dx>\frac{{\{(M-1-m)!\}}^2(2(M-m)-1)}{{(2s)}^{2(M-m)-1}}.$$

(11)

The following are the examples of Theorem 1 and Corollary 1.

Example 1 The following example corresponds to the case $M=1$ and $r(x)=-6/(-11s^2+2sx+x^2)$ of (4) with the clamped-free boundary condition

$$\{\begin{array}{c}-u^{″}(x)+\frac{6}{-11s^2+2sx+x^2}u(x)=0,\hfill \\ u(-s)=u^{\prime }(s)=0.\hfill \end{array}$$

It is easy to see that $u(x)=-(s+x)(11s^2-2sx-x^2)$ is the solution of the above equation. Moreover, it holds that

$${\int }_{-s}^s{r}^{+}(x)dx={\int }_{-s}^s-\frac{6}{-11s^2+2sx+x^2}dx=\frac{\sqrt{3}log(2+\sqrt{3})}{2s}>\frac{1}{C_{CF}(1,0,2)}=\frac{1}{2s}.$$

Example 2 The following example corresponds to the case $M=2$, $m=1$ and $r(x)=(3(17s^2-6sx+x^2))/(2{(7s^2-4sx+x^2)}^2)$ of (10) with the clamped-free boundary condition

$$\{\begin{array}{c}u(x)u^{(4)}(x)-\frac{3(17s^2-6sx+x^2)}{2{(7s^2-4sx+x^2)}^2}{(u^{\prime }(x))}^2=0,\hfill \\ u(-s)=u^{\prime }(-s)=u^{″}(s)=u^{‴}(s)=0.\hfill \end{array}$$

It is easy to see that $u(x)={(s+x)}^2(17s^2-6sx+x^2)$ is the solution of the above equation. Moreover, it holds that

$${\int }_{-s}^s{r}^{+}(x)dx={\int }_{-s}^s\frac{3(17s^2-6sx+x^2)}{2{(7s^2-4sx+x^2)}^2}dx=\frac{3+2\sqrt{3}\pi }{12s}>\frac{1}{C_{CF}(2,1,2)}=\frac{1}{2s}.$$

3 Proof of Proposition 2

Assuming Proposition 1, we first prove Proposition 2.

Proof of Proposition 2 Let u be a solution of equation (4). Since u satisfies the clamped-free boundary condition, multiplying (4) by u and integrating it over $[-s,s]$, we have

$$\begin{array}{rcl}{\int }_{-s}^s{(u^{(M)}(x))}^{2}dx& =& {\int }_{-s}^s{(-1)}^{M}u(x)u^{(2M)}(x)dx={\int }_{-s}^{s}r(x){(u(x))}^{2}dx\\ \le & {\left(\underset{-s\le x\le s}{sup}|u(x)|\right)}^2{\int }_{-s}^s{r}^{+}(x)dx\\ \le & C(M,0,2){\int }_{-s}^s{(u^{(M)}(x))}^{2}dx{\int }_{-s}^s{r}^{+}(x)dx.\end{array}$$

(12)

Here, if $u^{(M)}\equiv 0$, then there exists ($i=0,\dots ,M-1$) such that $u(x)={\sum }_{i=0}^{M-1}{a}_i{x}^i$. Since u satisfies the clamped boundary condition at $x=-s$, we have $u\equiv 0$. This contradicts the assumption that u is a non-trivial solution of (4). So, canceling ${\parallel u^{(M)}\parallel }_2^2$, we obtain

$${\int }_{-s}^s{r}^{+}(x)dx\ge \frac{1}{C_{CF}(M,0,2)}.$$

(13)

Next, we show that the inequality (13) is strict. To see this, we note that in (12), if the equality holds for the first inequality, then u is a constant. But, again from the clamped boundary condition at $x=-s$, we have $u\equiv 0$. Thus, the inequality is strict. Finally, we see (5) is sharp. For this purpose, let us define the functional

$$J(\varphi ):=\frac{{\int }_{-s}^s{|{\varphi }^{(M)}|}^{2}dx}{{\int }_{-s}^s\tilde{r}{|\varphi |}^{2}dx}(\varphi \in W(M,2),\varphi \not\equiv 0),$$

where is defined later. By the standard argument of the variational method, J has the minimizer $u\in W(M,2)$ (see, for example, [[16], Lemma 3]), i.e.,

$${\lambda }_1:=\underset{\varphi \in W(M,2),\varphi \not\equiv 0}{min}J(\varphi )=J(u).$$

Hence, it satisfies the Euler-Lagrange equation (as a classical solution by the regularity argument)

$${(-1)}^M{u}^{(2M)}(x)={\lambda }_1\tilde{r}(x)u(x)(-s\le x\le s).$$

(14)

Further, it holds that

$$\begin{array}{rcl}{\lambda }_1& =& \underset{\varphi \in W(M,2),\varphi \not\equiv 0}{min}\frac{{\int }_{-s}^s{|{\varphi }^{(M)}|}^{2}dx}{{\int }_{-s}^s\tilde{r}{|\varphi |}^{2}dx}>\frac{{\int }_{-s}^s{|{\varphi }^{(M)}|}^{2}dx}{{({sup}_{-s\le x\le s}|\varphi |)}^2{\int }_{-s}^s\tilde{r}dx}\\ \ge & \frac{1}{C_{CF}(M,0,2){\int }_{-s}^s\tilde{r}dx}.\end{array}$$

(15)

Here, let us fix $\tilde{r}$ as

$$\tilde{r}(x):=\{\begin{array}{cc}\frac{x-s}{\delta }+1\hfill & (s-\delta <x\le s),\hfill \\ 0\hfill & (-s\le x\le s-\delta ).\hfill \end{array}$$

For such $\tilde{r}$, let us substitute $\varphi =u_{\ast }$ (of Proposition 1) into (15). It is easy to see that $u_{\ast }$ takes its maximum at $x=s$, hence by taking δ sufficiently small, we see that the right-hand side of (15) can be arbitrarily close to the left-hand side, i.e., for a small positive ${ϵ}_1$, ${\lambda }_1$ can be written as

$${\lambda }_1=\frac{1}{C_{CF}(M,0,2){\int }_{-s}^s\tilde{r}dx}+{ϵ}_1.$$

(16)

Putting $r={\lambda }_1\tilde{r}$, we see from (14) a solution u of

$${(-1)}^M{u}^{(2M)}(x)=r(x)u(x)(-s\le x\le s)$$

(17)

exists, and from (16) r satisfies

$${\int }_{-s}^{s}r(x)dx=\frac{1}{C(M,0,2)}+{ϵ}_1{\int }_{-s}^s\tilde{r}dx=\frac{1}{C(M,0,2)}+{ϵ}_2.$$

(18)

Hence, (5) is sharp. □

Proof of Corollary 1 Integrating equation (10), we have

$$\begin{array}{rcl}{\int }_{-s}^s{(u^{(M)}(x))}^{2}dx& =& {\int }_{-s}^{s}r(x){(u^{(m)}(x))}^{2}dx\le {\left(\underset{-s\le x\le s}{sup}|u^{(m)}(x)|\right)}^2{\int }_{-s}^s{r}^{+}(x)dx\\ \le & C(M,m,2){\int }_{-s}^s{(u^{(M)}(x))}^{2}dx{\int }_{-s}^s{r}^{+}(x)dx.\end{array}$$

(19)

As in the proof of Proposition 2, by canceling ${\parallel u^{(M)}\parallel }_2^2$, we have

$${\int }_{-s}^s{r}^{+}(x)dx\le \frac{1}{C_{CF}(M,m,2)}.$$

Next, we show that the inequality (11) is strict. To see this, we note that in (19), the equality holds for the first inequality if and only if $u^{(m)}$ is a constant. Hence, from the clamped boundary condition at $x=-s$, we have $u^{(m)}\equiv 0$. So, there exists ($i=0,\dots ,m-1$) such that $u(x)={\sum }_{i=0}^{m-1}{a}_i{x}^i$. But, again from the clamped boundary condition at $x=-s$, we have $u\equiv 0$. Thus, inequality (11) is strict. □

4 Proof of Proposition 1

We prepare the following lemmas for the proof of Proposition 1.

Lemma 1 Suppose there exists a function $u_{\ast }\in W(M,p)$ which attains the best constant $C(M,n,p)$ of (6), then it holds that

$$\underset{-s\le x\le s}{max}|u_{\ast }^{(m)}(x)|=|u_{\ast }^{(m)}(s)|.$$

Proof Suppose it holds that

$$\underset{-s\le x\le s}{max}|u_{\ast }^{(m)}(x)|=|u_{\ast }^{(m)}(a)|,$$

where $a\not\equiv s$. Further, let us define

$$\tilde{u}(x):=\{\begin{array}{cc}0\hfill & (-s\le x\le -a),\hfill \\ u_{\ast }(x+a-s)\hfill & (-a\le x\le s).\hfill \end{array}$$

Then it holds $\tilde{u}\in W(M,p)$ and

$$\underset{-s\le x\le s}{max}|{\tilde{u}}^{(m)}(x)|=\underset{-s\le x\le s}{max}|u_{\ast }^{(m)}(x)|=|u_{\ast }^{(m)}(a)|$$

and ${\parallel {\tilde{u}}^{(M)}\parallel }_{L^p(-s,s)}<{\parallel u_{\ast }^{(M)}\parallel }_{L^p(-s,s)}$. Hence,

$$C(M,m,p)=\frac{{({max}_{-s\le x\le s}|u_{\ast }^{(m)}(x)|)}^p}{{\parallel u_{\ast }^{(M)}\parallel }_{L^p(-s,s)}}<\frac{{({max}_{-s\le x\le s}|{\tilde{u}}^{(m)}(x)|)}^p}{{\parallel {\tilde{u}}^{(M)}\parallel }_{L^p(-s,s)}}.$$

This contradicts the assumption that $C(M,m,p)$ is the best constant of (6). □

Lemma 2 Let

$$H_m(x):=\frac{{(-1)}^{M-1-m}{(x-s)}^{M-1-m}}{(M-1-m)!},$$

then for $u\in W(M,p)$ it holds that

$$u^{(m)}(s)={\int }_{-s}^s{u}^{(M)}(x)H_m(x)dx.$$

(20)

Proof Integrating by parts, we obtain the result. □

Proof of Proposition 1 From Lemma 2, we see that if the function attains the best constant $C(M,m,p)$, it belongs to $W_{\ast }(M,m,p)\subset W(M,p)$:

$$W_{\ast }(M,m,p)=\{u\in W(M,p)|\underset{-s\le x\le s}{max}|u^{(m)}(x)|=|u^{(m)}(s)|\}.$$

Let $u\in W_{\ast }(M,m,p)$. Then applying Hölder’s inequality to (20), we have

$$\underset{-s\le x\le s}{max}|u^{(m)}(x)|=|u^{(m)}(s)|\le {\parallel H_m\parallel }_{L^q(-s,s)}{\parallel u^{(M)}\parallel }_{L^p(-s,s)},$$

(21)

where q satisfies $1/p+1/q=1$. Hence, if there exists the function $u_{\ast }\in W_{\ast }(M,m,p)$ which attains the equality of (21), it holds that $C(M,m,p)={\parallel H_m\parallel }_{L^q(-s,s)}^p$. On the contrary, we see that the equality holds for (21) if and only if u satisfies

$$u^{(M)}(x)=(sgn{H}_m(x)){|H_m(x)|}^{q-1}.$$

(22)

It is easy to see that

$$u_{\ast }(x)={\int }_{-s}^x\frac{{(x-t)}^{m-1}}{(M-1)!}(sgn{H}_m(t)){|H_m(t)|}^{q-1}dt={\int }_{-s}^x\frac{{(x-t)}^{m-1}}{(M-1)!}{\left\{\frac{{(s-t)}^{M-1-m}}{(M-1-m)!}\right\}}^{\frac{1}{p-1}}dt$$

satisfies (22) and belongs to $W_{\ast }(M,m,p)$. Thus, we have shown $C(M,m,p)={\parallel H_m\parallel }_{L^q(-s,s)}^p$. Now, we compute ${\parallel H_m\parallel }_{L^q(-s,s)}^p$. It is

$$\begin{array}{rcl}{\parallel H_m\parallel }_{L^q(-s,s)}^p& =& \frac{1}{{\{(M-1-m)!\}}^p}{\left\{{\int }_{-s}^s{(s-x)}^{q(M-1-m)}dx\right\}}^{\frac{p}{q}}\\ =& \frac{1}{{\{(M-1-m)!\}}^p}{\left\{\frac{(p-1){(2s)}^{\frac{p(M-m)-1}{p-1}}}{p(M-m)-1}\right\}}^{p-1}.\end{array}$$

This completes the proof. □