Abstract
In this paper, we study a convergence theorem for a finite second-order Markov chain indexed by a general infinite tree with uniformly bounded degree. Meanwhile, the strong law of large numbers (LLN) and Shannon-McMillan theorem for a finite second-order Markov chain indexed by this tree are obtained.
2000 Mathematics Subject Classification: 60F15; 60J10.
Similar content being viewed by others
1. Introduction
A tree is a graph G = {T, E} that is connected and contains no circuits. Given any two vertices σ, t(σ ≠ t ∈ T), let be the unique path connecting σ and t. Define the graph distance d(σ, t) to be the number of edges contained in the path .
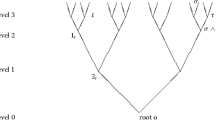
Let TC,Nbe a Cayley tree. In this tree, the root (denoted by o) has only N neighbors, and all other vertices have N + 1 neighbors. Let TB,Nbe a Bethe tree, on which each vertex has N + 1 neighboring vertices. Here, both TC,Nand TB,Nare homogeneous tree. An infinite tree with uniformly bounded degree is that the numbers of neighbors of any vertices in this tree are uniformly bounded. Therefore, the homogeneous tree is the special case of infinite tree with uniformly bounded degree. In this paper, we mainly consider a general infinite tree with uniformly bounded degree, that is, the tree is formed by an infinite tree that has uniformly bounded degree with the root o connecting with another point denoted by the root -1. In order to understand this tree graph, we give a figure (see Figure 1), which is formed by a TC,2with the root o connecting with another root -1. When the context permits, this type of trees is all denoted simply by T.
Let σ, t(σ, t ≠ o, -1) be vertices of a general infinite tree with uniformly bounded degree T. Write t ≤ σ if t is on the unique path connecting o to σ, and |σ| for the number of edges on this path. For any two vertices σ, t(σ, t ≠ o, -1) of tree T, denote by σ ∧ t the vertex farthest from o satisfying σ ∧ t ≤ σ and σ ∧ t ≤ t.
The set of all vertices with distance n from root o is called the n th generation of T, which is denoted by L n . We say that L n is the set of all vertices on level n and especially root-1 is on the -1st level on tree T. We denote by T(n)the subtree of a general infinite tree with uniformly bounded degree T containing the vertices from level -1 (the root -1) to level n. Let t(≠ o, -1) be a vertex of a general infinite tree with uniformly bounded degree T. Predecessor of the vertex t is another vertex that is nearest from t on the unique path from root -1 to t. We denote the predecessor of t by 1 t and the predecessor of 1 t by 2 t . We also say that 2 t is the second predecessor of t. XA = {X t , t ∈ A} and denoted by |A| the number of vertices of A, and xA is the realization of XA.
Definition 1 Let G = {1, 2, ..., N} and P(z|y, x) be a nonnegative functions on G3. Let
If
P will be called a second-order transition matrix.
Definition 2 Let T be a general infinite tree, G = {1, 2, ..., N} be a finite state space, and {X t , t ∈ T} be a collection of G-valued random variables defined on the probability space . Let
be a distribution on G2, and
be a second-order transition matrix. If for any vertex t (t ≠ o, -1),
and
{X t , t ∈ T} will be called a G-valued second-order Markov chain indexed by a general infinite tree T with the initial distribution (1) and second-order transition matrix (2) or called a T-indexed second-order Markov chain.
The subject of tree-indexed processes is rather young. Benjamini and Peres (see [1]) have given the notion of the tree-indexed Markov chains and studied the recurrence and ray-recurrence for them. Berger and Ye (see [2]) have studied the existence of entropy rate for some stationary random fields on a homogeneous tree. Ye and Berger (see [3, 4]), by using Pemantle's result(see [5]) and a combinatorial approach, have studied the Shannon- McMillan theorem with convergence in probability for a PPG-invariant and ergodic random field on a homogeneous tree. Yang and Liu(see [6])have studied a strong law of large numbers for the frequency of occurrence of states for Markov chains field on a homogeneous tree (a particular case of tree-indexed Markov chains field and PPG-invariant random field). Yang (see [7]) has studied the strong law of large numbers for frequency of occurrence of state and Shannon-McMillan theorem for homogeneous Markov chains indexed by a homogeneous tree. Takacs (see [8]) has studied the strong law of large numbers for the univariate functions of finite Markov chains indexed by an infinite tree with uniformly bounded degree. Recently, Yang (see [9]) has studied the strong law of large numbers and Shannon-McMillan theorem for nonhomogeneous Markov chains indexed by a homogeneous tree. Huang and Yang (see [10]) have studied the strong law of large numbers for Markov chains indexed by an infinite tree with uniformly bounded degree, which generalize the result of [8]. Shi and Yang (see [11]) have also studied a limit property of random transition probability for a second-order nonhomogeneous Markov chains indexed by a tree.
In this paper, we first study a convergence theorem for a finite second-order Markov chain indexed by a general infinite tree with uniformly bounded degree. As corollaries, we obtain some limit theorems for the frequencies of occurrence of states for this Markov chain. Finally, we obtain the strong law of large numbers and Shannon-McMillan theorem for a class of finite second-order Markov chain indexed by a general infinite tree with uniformly bounded degree.
2. Strong limit theorems
Lemma 1 Let T be a general infinite tree with uniformly bounded degree. Let {X t , t ∈ T} be a T-indexed second-order Markov chain with state space G defined as in Definition 2, {g t (x, y, z), t ∈ T} be a collection of functions defined on G3. Let L-1 = {-1}, L0 = {o} and . Set
and
where λ is a real number. Then is a nonnegative martingale.
Proof: The proof of Lemma 1 is similar to Lemma 2.1 in [9], so we omit it.
Theorem 1 Let {X t , t ∈ T} and {g t (x, y, z), t ∈ T} be defined as Lemma 1,
and {a n , n ≥ 1} be a sequence of nonnegative random variables. Let a > 0. Set
and
Then
Proof: By Lemma 1, we have known that is a nonnegative martingale. According to Doob martingale convergence theorem, we have
By (10) we have
By (5), (6) and (11), we get
By (12) and inequalities ln x ≤ x - 1 (x > 0), , as 0 < |λ| ≤ a we have
Letting 0 < λ ≤ a, by (13), we have
Let λ → 0+ in (14), by (8) we have
Taking -a ≤ λ < 0 in (15), similarly we get
Combining (7), (15) and (16), we obtain (9).
Corollary 1 Let {X t , t ∈ T} be a general infinite tree T with uniformly bounded degree defined by Definition 2. Let {g t (x, y, z), t ∈ T} be a collection of uniformly bounded functions defined on G3. That is, there exists K > 0 such that |g t (x, y, z)| ≤ K. F n (ω) and G n (ω) be given by (5) and (7), respectively. Let N ≥ 0, then
Proof: Letting a n = |T(n+N)| in Theorem 1, noticing that {g t (x, y), t ∈ T} are uniformly bounded, and then D(α) = Ω for all α > 0. This corollary follows from Theorem 1 directly.
In the following, let . We always let N ≥ 0, m, l, k ∈ G, d0(t) := 1 and denoted by
Corollary 2 Let T be a general infinite tree with uniformly bounded degree. Let {X t , t ∈ T} be a T-indexed second-order Markov chain with state space G defined by Definition 2. Then for all m, l, k ∈ G, N ≥ 0, we have
Proof: Because of the uniformly bounded degree of T, there is a < ∞ with dN(t) < aN. Let g t (x, y, z) = dN(t)I l (y)I k (z), a n = |T(n+N)|. Obviously, {g t (x, y, z), t ∈ T} are uniformly bounded. Since
and
This corollary follows from Corollary 1 directly.
Corollary 3 Let {X t , t ∈ T} be a second-order Markov chain taking values in G indexed by a general infinite tree with uniformly bounded degree defined as before. Then for all m, l, k ∈ G, we have
Proof: Let g t (x, y, z) = dN(t) I m (x)I l (y)I k (z), a n = |T(n+N)|. Obviously, {g t (x, y, z), t ∈ T} are uniformly bounded. Since
and
This corollary follows from Corollary 1 directly.
3. LLN and Shannon-McMillan theorems
In this section, we study the strong law of large numbers and the Shannon-McMillan theorems for a second-order Markov chain indexed by a general infinite tree with uniformly bounded degree. In the following, we first give a definition and a lemma.
Definition 3 Let G = (1, 2, ..., N) be a finite state space, and
be a second-order transition matrix. Define a stochastic matrix as follows:
where
Then is called a two-dimensional stochastic matrix determined by the second-order transition matrix P.
Lemma 2 (see [12])
Let be a two-dimensional stochastic matrix determined by the second-order transition matrix P. If the elements of P are all positive, i.e.,
then is ergodic.
Theorem 2 Let T be a general infinite tree with uniformly bounded degree. Let {X t , t ∈ T} be a T-indexed second-order Markov chain taking values in G generated by P. Let the two-dimensional stochastic matrix determined by P be ergodic. Then for all m, l, k ∈ G, we have
where {π(l, k), l, k ∈ G} is the stationary distribution determined by .
Proof: By (21) and (29), we have
We now prove the following equation by induction: Fixed N ≥ 0 and for all h ≥ 1, we have
The case h = 1 is immediate from the equation (32). The case h + 1 follows by
Notice that the first term vanishes as n → ∞, because of the induction hypothesis. According to the equation (32), the second term approximates to zero as n → ∞. By induction, we have (33) holds for all h ≥ 1. Since . By (33), we have
Since
(30) follows from (35) and (36), (31) follows from (30) and (24).
Corollary 4 Under the conditions of Theorem 2, let . Then
Let T be a tree, {X t , t ∈ T} be a stochastic process indexed by tree T taking values in G, be the realization of . Denote
Let
f n (ω) is called the entropy density of . If {X t , t ∈ T} is a second-order Markov chain indexed by a general infinite tree with uniformly bounded tree defined as in Definition 2, we easily have
The convergence of f n (ω) to a constant in a sense (L1 convergence, convergence in probability, a.e. convergence) is called the Shannon-McMillan theorem, or the entropy theorem or the AEP in information theory. Here from Theorems 1, 2, and Corollary 4, we can easily obtain the Shannon-McMillan theorem with a.e. convergence for a second-order Markov chain indexed by a general infinite tree with uniformly bounded tree.
Theorem 3 Let {X t , t ∈ T} be a second-order Markov chain taking values in G indexed by a general infinite tree with uniformly bounded tree T, and f n (ω) be defined as (38). Then
Proof:
Equation (39) follows from (40) and (37) directly.
References
Benjamini I, Peres Y: Markov chains indexed by trees. Ann Probab 1994, 22: 219–243. 10.1214/aop/1176988857
Berger T, Ye Z: Entropic aspects of random fields on trees. IEEE Trans Inform Theory 1990, 36: 1006–1018. 10.1109/18.57200
Ye Z, Berger T: Ergodic, regularity and asymptotic equipartition property of random fields on trees. Comb Inform Syst Sci 1996, 21: 157–184.
Ye Z, Berger T: Information Measure for Discrete Random Field. Science, Beijing 1998.
Pemantle R: Andomorphism invariant measure on tree. Ann Probab 1992, 20: 1549–1566. 10.1214/aop/1176989706
Yang WG, Liu W: Strong law of large numbers for Markov chains fields on a bethe tree. Statist Probab Lett 2000, 49: 245–250. 10.1016/S0167-7152(00)00053-5
Yang WG: Some limit properties for Markov chains indexed by a homogeneous tree. Statist Probab Lett 2003, 65: 241–250. 10.1016/j.spl.2003.04.001
Takacs C: Strong law of large numbers for branching Markov chains. Markov Process. Relat Fields 2001, 8: 107–116.
Yang WG, Ye Z: The Asymptotic Equipartition property for Markov chains indexed by a Homogeneous tree. IEEE Trans Inform Theory 2007, 53(9):3275–3280.
Huang HL, Yang WG: Strong law of large numbers for Markov chains indexed by an infinite tree with uniformly bounded degree. Sci China 2008, 51(2):195–202. 10.1007/s11425-008-0015-1
Shi ZY, Yang WG: Some limit properties of random transition probability for second-order nonhomogeneous Markov chains indexed by a tree. J Inequal Appl 2009. ID 503203
Yang WG, Liu W: The asymptotic equipartition property for Mth-order nonhomogeneous Markov information sources. IEEE Trans Inf Theory 2004, 50(12):3326–3330. 10.1109/TIT.2004.838339
Acknowledgements
The authors would like to thank the referees for their valuable suggestions and comments. This work is supported by the Research Foundation for Advanced Talents of Jiangsu University(11JDG116) and the National Natural Science Foundation of China (11071104, 11171135, 71073072).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
ZS, WY and LT carried out the design of the study and performed the analysis. QZ participated in its design and coordination. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shi, Z., Yang, W., Tian, L. et al. Some limit theorems for the second-order Markov chains indexed by a general infinite tree with uniform bounded degree. J Inequal Appl 2012, 2 (2012). https://doi.org/10.1186/1029-242X-2012-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-2