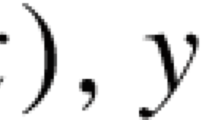Modified Proximal point algorithms for finding a zero point of maximal monotone operators, generalized mixed equilibrium problems and variational inequalities

Abstract

In this article, we prove strong and weak convergence theorems of modified proximal point algorithms for finding a common element of the zero point of maximal monotone operators, the set of solutions of generalized mixed equilibrium problems, the set of solutions of variational inequality problems and the fixed point set of relatively nonexpansive mappings in a Banach space under difference conditions. Our results modify and improve previous result of Li and Song.

Mathematics Subject Classification 2000: 47H09; 47H10.

1. Introduction

Let E be a Banach space with norm || · ||, C be a nonempty closed convex subset of E and let E* denote the dual of E. Let B be a monotone operator of C into E*. The variational inequality problem is to find a point x ∈ C such that

$$⟨Bx,y-x⟩\ge 0\text{for all }y\in C.$$

(1.1)

The set of solutions of the variational inequality problem is denoted by V I(C, B). Such a problem is connected with the convex minimization problem, the complementarity problem, the problem of finding a point u ∈ E satisfying 0 = Bu and so on. An operator B of C into E* is said to be inverse-strongly monotone, if there exists a positive real number α such that

$$⟨x-y,Bx-By⟩\ge \alpha {∥Bx-By∥}^2$$

(1.2)

for all x, y ∈ C. In such a case, B is said to be α-inverse-strongly monotone. If an operator B of C into E* is α-inverse-strongly monotone, then B is Lipschitz continuous, that is $∥Bx-By∥\le \frac{1}{\alpha }∥x-y∥$ for all x, y ∈ C.

A point x ∈ C is a fixed point of a mapping S: C → C if Sx = x, by F(S) denote the set of fixed points of S; that is, F(S) = {x ∈ C: Sx = x}. A point p in C is said to be an asymptotic fixed point of S (see [1]) if C contains a sequence {x _n } which converges weakly to p such that lim_n→∞||x _n - Sx _n || = 0. The set of asymptotic fixed points of S will be denoted by $\hat{F}\left(S\right)$. A mapping S from C into itself is said to be relatively nonexpansive [2–4] if $\hat{F}\left(S\right)=F\left(S\right)$and ϕ(p, Sx) ≤ ϕ(p, x) for all x ∈ C and p ∈ F(S). The asymptotic behavior of a relatively nonexpansive mapping was studied in [5, 6]. A mapping S is said to be ϕ-nonexpansive, if ϕ(Sx, Sy) ≤ ϕ(x, y) for x, y ∈C. A mapping S is said to be quasi ϕ-nonexpansive if $F\left(S\right)\ne \cancel{0}$ and ϕ(p, Sx) ≤ ϕ(p, x) for x ∈ C and p ∈ F(S).

Let E be a Banach space with norm || · ||, C be a nonempty closed convex subset of E and let E* be the dual of E. Let Θ: C × C → ℝ be a bifunction, φ: C → ℝ be a real-valued function, and B: C → E* be a nonlinear mapping. The generalized mixed equilibrium problem, which is to find x ∈ C such that

$$\Theta \left(x,y\right)+⟨Bx,y-x⟩+\phi \left(y\right)-\phi \left(x\right)\ge 0,\forall y\in C.$$

(1.3)

The solutions set to (1.3) is denoted by Ω, i.e.,

$$\Omega =\left\{x\in C:\Theta \left(x,y\right)+⟨Bx,y-x⟩+\phi \left(y\right)-\phi \left(x\right)\ge 0,\forall y\in C\right\}.$$

(1.4)

If B = 0, the problem (1.3) reduce into the mixed equilibrium problem for Θ, denoted by MEP(Θ, φ), which is to find x ∈ C such that

$$\Theta \left(x,y\right)+\phi \left(y\right)-\phi \left(x\right)\ge 0,\forall y\in C.$$

(1.5)

If Θ ≡ 0, the problem (1.3) reduce into the mixed variational inequality of Browder type, denoted by V I(C, B, φ), is to find x ∈ C such that

$$⟨Bx,y-x⟩+\phi \left(y\right)-\phi \left(x\right)\ge 0,\forall y\in C.$$

(1.6)

If B = 0 and φ = 0 the problem (1.3) reduce into the equilibrium problem for Θ, denoted by EP(Θ), is to find x ∈ C such that

$$\Theta \left(x,y\right)\ge 0,\forall y\in C.$$

(1.7)

The above formulation (1.7) was shown in [7] to cover monotone inclusion problems, saddle point problems, variational inequality problems, minimization problems, optimization problems, variational inequality problems, vector equilibrium problems, Nash equilibria in noncooperative games. In addition, there are several other problems, for example, the complementarity problem, fixed point problem and optimization problem, which can also be written in the form of an EP(Θ). In other words, the EP(Θ) is an unifying model for several problems arising in physics, engineering, science, optimization, economics, etc. In the last two decades, many articles have appeared in the literature on the existence of solutions of EP(Θ); see, for example [7–10] and references therein. Some solution methods have been proposed to solve the EP(Θ) (see, for example, [8, 10–15] and references therein). In 2005, Combettes and Hirstoaga [11] introduced an iterative scheme of finding the best approximation to the initial data when EP(Θ) is nonempty and they also proved a strong convergence theorem.

In 2004, in Hilbert space H, Iiduka et al. [16] proved that the sequence {x _n } defined by: x₁ = x ∈ C and

$$x_{n+1}=P_C\left(x_n-{\lambda }_{n}B{x}_n\right),$$

(1.8)

where P _C is the metric projection of H onto C and {λ _n } is a sequence of positive real numbers, converges weakly to some element of V I(C, B).

In 2008, Iiduka and Takahashi [17] introduced the following iterative scheme for finding a solution of the variational inequality problem for an inverse-strongly monotone operator B that satisfies the following conditions in a 2-uniformly convex and uniformly smooth Banach space E:

(C1) B is inverse-strongly monotone,

(C2) $VI\left(C,B\right)\ne \cancel{0}$,

(C3) ||Ay|| ≤ || Ay - Au|| for all y ∈ C and u ∈ V I(C, B).

Let x₁ = x ∈ C and

$$x_{n+1}={\Pi }_C{J}^{-1}\left(J{x}_n-{\lambda }_{n}B{x}_n\right)$$

(1.9)

for every n = 1, 2, 3, ..., where Π _C is the generalized metric projection from E onto C, J is the duality mapping from E into E* and {λ _n } is a sequence of positive real numbers. They proved that the sequence {x _n } generated by (1.9) converges weakly to some element of V I(C, B).

Consider the problem of finding:

$$v\in E\text{such that }0\in A\left(v\right),$$

(1.10)

where A is an operator from E into E*. Such v ∈ E is called a zero point of A. When A is a maximal monotone operator, a well-know methods for solving (1.10) in a Hilbert space H is the proximal point algorithm: x₁ = x ∈ H and,

$$x_{n+1}=J_{r_n}{x}_n,n=1,2,3,\dots ,$$

(1.11)

where {r _n } ⊂ (0, ∞) and $J_{r_n}={\left(I+r_{n}A\right)}^{-1}$, then Rockafellar [18] proved that the sequence {x _n } converges weakly to an element of A^-1(0). Such a problem contains numerous problems in economics, optimization, and physics and is connected with a variational inequality problem. It is well known that the variational inequalities are equivalent to the fixed point problems.

In 2000, Kamimura and Takahashi [19] proved the following strong convergence theorem in Hilbert spaces, by the following algorithm

$$x_{n+1}={\alpha }_{n}x+\left(1-{\alpha }_n\right)J_{r_n}{x}_n,n=1,2,3,\dots ,$$

(1.12)

where J _r = (I + rA)^-1 J, then the sequence {x _n } converges strongly to $P_{A^{-1}0}\left(x\right)$, where $P_{A^{-1}0}$ is the projection from H onto A^-1(0). These results were extended to more general Banach spaces see [20, 21].

In 2003, Kohsaka and Takahashi [21] introduced the following iterative sequence for a maximal monotone operator A in a smooth and uniformly convex Banach space: x₁ = x ∈ E and

$$x_{n+1}=J^{-1}\left({\alpha }_{n}Jx+\left(1-{\alpha }_n\right)J\left(J_{r_n}{x}_n\right)\right),n=1,2,3,\dots ,$$

(1.13)

where J is the duality mapping from E into E* and J _r = (I + rA)^-1J.

In 2004, Kamimura et al. [22] considered the algorithm (1.14) in a uniformly smooth and uniformly convex Banach space E, namely

$$x_{n+1}=J^{-1}\left({\alpha }_{n}J{x}_n+\left(1-{\alpha }_n\right)J\left(J_{r_n}{x}_n\right)\right),n=1,2,3,\dots .$$

(1.14)

They proved that the algorithm (1.14) converges weakly to some element of A^-10.

In 2008, Li and Song [23] proved a strong convergence theorem in a Banach space, by the following algorithm: x₁ = x ∈ E and

$$\begin{array}{c}{y}_n=J^{-1}\left({\beta }_{n}J\left(x_n\right)+\left(1-{\beta }_n\right)J\left(J_{r_n}{x}_n\right)\right),\hfill \\ x_{n+1}=J^{-1}\left({\alpha }_{n}Jx+\left(1-{\alpha }_n\right)J\left(y_n\right)\right),\hfill \end{array}$$

(1.15)

with the coefficient sequences {α _n }, {β _n } ⊂ [0, 1] and {r _n } ⊂ (0, ∞) satisfying lim_{n→ ∞}α _n = 0, ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$, lim_n→∞β _n = 0, and lim_n→∞r _n = ∞, where J is the duality mapping from E into E* and J _r = (I + rA)^-1 J. Then they proved that the sequence {x _n } converges strongly to Π _C x, where Π _C is the generalized projection from E onto C.

In this article, motivated and inspired by Kamimura et al. [22], Li and Song [23], Iiduka and Takahashi [17], Zhang [24] and Inoue et al. [25], we introduce the new hybrid algorithm (3.1) below. Under appropriate difference conditions, we will prove that the sequence {x _n } generated by algorithms (3.1) converges strongly to the point ${\prod }_{\Omega \cap VI\left(C,A\right)\cap A^{-1}\left(0\right)\cap F\left(S\right)}{x}_0$ and converges weakly to the point ${\text{lim}}_{n\to \infty }{\prod }_{\Omega \cap VI\left(C,A\right)\cap A^{-1}\left(0\right)\cap F\left(S\right)}{x}_n$. The results presented in this article extend and improve the corresponding ones announced by Kamimura et al. [22], Li and Song [23] and some authors in the literature.

2. Preliminaries

A Banach space E is said to be strictly convex if $∥\frac{x+y}{2}∥<1$ for all x, y ∈ E with ||x|| = ||y|| = 1 and x ≠ y. Let U = {x ∈ E: ||x|| = 1} be the unit sphere of E. Then the Banach space E is said to be smooth provided

$$\underset{t\to 0}{\text{lim}}\frac{∥x+ty∥-∥x∥}{t}$$

exists for each x, y ∈ U. It is also said to be uniformly smooth if the limit is attained uniformly for x, y ∈ E. The modulus of convexity of E is the function δ: [0, 2] → [0, 1] defined by

$$\delta \left(\epsilon \right)=\text{inf}\left\{1-∥\frac{x+y}{2}∥:x,y\in E,∥x∥=∥y∥=1,∥x-y∥\ge \epsilon \right\}.$$

(2.1)

A Banach space E is uniformly convex if and only if δ(ε) > 0 for all ε ∈ (0, 2]. Let p be a fixed real number with p ≥ 2. A Banach space E is said to be p-uniformly convex if there exists a constant c > 0 such that δ(ε) ≥ cε^p for all ε ∈ [0, 2] (see [26, 27] for more details). Observe that every p-uniform convex is uniformly convex. One should note that no a Banach space is p-uniform convex for 1 < p < 2. It is well known that a Hilbert space is 2-uniformly convex and uniformly smooth. For each p > 1, the generalized duality mapping $J_p:E\to 2^{E^{*}}$ is defined by

$$J_p\left(x\right)=\left\{x^{*}\in E^{*}:⟨x,x^{*}⟩={\left|\right|x\left|\right|}^p,\left|\right|x^{*}\left|\right|={\left|\right|x\left|\right|}^{p-1}\right\}$$

(2.2)

for all x ∈ E. In particular, J = J₂ is called the normalized duality mapping. If E is a Hilbert space, then J = I, where I is the identity mapping. It is also known that if E is uniformly smooth, then J is uniformly norm-to-norm continuous on each bounded subset of E.

We know the following (see [28]):

• (1) if E is smooth, then J is single-valued;

• (2) if E is strictly convex, then J is one-to-one and 〈x - y, x* - y*〉 > 0 holds for all (x, x*), (y, y*) ∈ J with x ≠ y;

• (3) if E is reflexive, then J is surjective;

• (4) if E is uniformly convex, then it is reflexive;

• (5) if E* is uniformly convex, then J is uniformly norm-to-norm continuous on each bounded subset of E.

The duality J from a smooth Banach space E into E* is said to be weakly sequentially continuous [29] if x _n ⇀ x implies Jx _n ⇀* Jx, where ⇀* implies the weak* convergence.

Lemma 2.1. [30, 31] If E be a 2-uniformly convex Banach space. Then, for all x, y ∈ E we have

$$∥x-y∥\le \frac{2}{c^2}∥Jx-Jy∥,$$

where J is the normalized duality mapping of E and 0 < c ≤ 1.

The best constant $\frac{1}{c}$ in Lemma is called the 2-uniformly convex constant of E (see [26]).

Lemma 2.2. [30, 32] If E be a p-uniformly convex Banach space and let p be a given real number with p ≥ 2. Then for all x, y ∈ E, J _x ∈ J _p (x) and J _y ∈ J _p (y)

$$⟨x-y,Jx-Jy⟩\ge \frac{c^p}{2^{p-2}p}{∥x-y∥}^p,$$

where J _p is the generalized duality mapping of E and $\frac{1}{c}$ is the p-uniformly convexity constant of E.

Lemma 2.3. (Xu [31]) Let E be a uniformly convex Banach space. Then for each r > 0, there exists a strictly increasing, continuous and convex function g: [0, ∞) → [0, ∞) such that g(0) = 0 and

$${∥\lambda x+\left(1-\lambda y\right)∥}^2\le \lambda {∥x∥}^2+\left(1-\lambda \right){∥y∥}^2-\lambda \left(1-\lambda \right)g\left(∥x-y∥\right)$$

(2.3)

for all x, y ∈{z ∈ E: ||z|| ≤ r} and λ ∈ [0, 1].

Let E be a smooth, strictly convex and reflexive Banach space and let C be a nonempty closed convex subset of E. Throughout this article, we denote by ϕ the function defined by

$$\varphi \left(x,y\right)={∥x∥}^2-2⟨x,Jy⟩+{∥y∥}^2,\text{for}x,y\in E.$$

(2.4)

Following Alber [33], the generalized projection Π _C : E → C is a map that assigns to an arbitrary point x ∈ E the minimum point of the functional ϕ(x, y), that is, ${\prod }_{C}x=\bar{x}$, where $\bar{x}$ is the solution to the minimization problem

$$\varphi \left(\bar{x},x\right)=\underset{y\in C}{\text{inf}}\varphi \left(y,x\right)$$

(2.5)

existence and uniqueness of the operator Π _C follows from the properties of the functional ϕ(x, y) and strict monotonicity of the mapping J. It is obvious from the definition of function ϕ that (see [33])

$${\left(∥y∥-∥x∥\right)}^2\le \varphi \left(y,x\right)\le {\left(∥y∥+∥x∥\right)}^2,\forall x,y\in E.$$

(2.6)

If E is a Hilbert space, then ϕ(x, y) = ||x - y||².

If E is a reflexive, strictly convex and smooth Banach space, then for x, y ∈ E, ϕ(x, y) = 0 if and only if x = y. It is sufficient to show that if ϕ(x, y) = 0 then x = y. From (2.6), we have ||x|| = ||y||. This implies that 〈x, Jy〉 = ||x||² = ||Jy||². From the definition of J, one has Jx = Jy. Therefore, we have x = y (see [28, 34] for more details).

Lemma 2.4. (Kamimura and Takahashi [20]) Let E be a uniformly convex and smooth real Banach space and let {x _n }, {y _n } be two sequences of E. If ϕ(x _n , y _n ) → 0 and either {x _n } or {y _n } is bounded, then ||x _n - y _n || → 0.

Lemma 2.5. (Alber [33]) Let C be a nonempty closed convex subset of a smooth Banach space E and x ∈ E. Then, x₀ = Π _C x if and only if

$$⟨x_0-y,Jx-J{x}_0⟩\ge 0,\forall y\in C.$$

Lemma 2.6. (Alber [33]) Let E be a reflexive, strictly convex and smooth Banach space, let C be a nonempty closed convex subset of E and let x ∈ E. Then

$$\varphi \left(y,{\Pi }_{C}x\right)+\varphi \left({\Pi }_{C}x,x\right)\le \varphi \left(y,x\right),\forall y\in C.$$

Let E be a strictly convex, smooth and reflexive Banach space, let J be the duality mapping from E into E*. Then J^-1 is also single-valued, one-to-one, and surjective, and it is the duality mapping from E* into E. Define a function V: E × E* → ℝ as follows (see [21]):

$$V\left(x,x^{*}\right)={∥x∥}^2-2⟨x,x^{*}⟩+{∥x^{*}∥}^2$$

(2.7)

for all x ∈ Ex ∈ E and x* ∈ E*. Then, it is obvious that V (x, x*) = ϕ(x, J^-1(x*)) and V (x, J(y)) = ϕ(x, y).

Lemma 2.7. (Kohsaka and Takahashi [[21], Lemma 3.2]) Let E be a strictly convex, smooth and reflexive Banach space, and let V be as in (2.7). Then

$$V\left(x,x^{*}\right)+2⟨J^{-1}\left(x^{*}\right)-x,y^{*}⟩\le V\left(x,x^{*}+y^{*}\right)$$

(2.8)

for all x ∈ E and x*, y* ∈ E*.

Let E be a reflexive, strictly convex and smooth Banach space. Let C be a closed convex subset of E. Because ϕ(x, y) is strictly convex and coercive in the first variable, we know that the minimization problem inf_y∈Cϕ(x, y) has a unique solution. The operator Π _C x: = arg min_y∈Cϕ(x, y) is said to be the generalized projection of x on C.

A set-valued mapping A: E → E* with domain $D\left(A\right)=\left\{x\in E:A\left(x\right)\ne \cancel{0}\right\}$ and range R(A) = {x* ∈ E*: x* ∈ A(x), x ∈ D(A)} is said to be monotone if 〈x - y, x* - y*〉 ≥ 0 for all x* ∈ A(x), y* ∈ A(y). We denote the set {s ∈ E: 0 ∈ Ax} by A^-10. A is maximal monotone if its graph G(A) is not properly contained in the graph of any other monotone operator. If A is maximal monotone, then the solution set A^-10 is closed and convex.

Let E be a reflexive, strictly convex and smooth Banach space, it is knows that A is a maximal monotone if and only if R(J + rA) = E* for all r > 0.

Define the resolvent of A by J _r x = x _r . In other words, J _r = (J + rA)^-1J for all r > 0. J _r is a single-valued mapping from E to D(A). Also, A^-1(0) = F(J _r ) for all r > 0, where F(J _r ) is the set of all fixed points of J _r . Define, for r > 0, the Yosida approximation of A by A _r = (J - JJ _r )/r. We know that A _r x ∈ A(J _r x) for all r > 0 and x ∈ E.

Lemma 2.8. (Kohsaka and Takahashi [[21], Lemma 3.1]) Let E be a smooth, strictly convex and reflexive Banach space, let A ⊂ E × E* be a maximal monotone operator with $A^{-1}0\ne \cancel{0}$, let r > 0 and let J _r = (J + rT)^-1J. Then

$$\varphi \left(x,J_{r}y\right)+\varphi \left(J_{r}y,y\right)\le \varphi \left(x,y\right)$$

for all x ∈ A^-10 and y ∈ E.

Let B be an inverse-strongly monotone mapping of C into E* which is said to be hemicontinuous if for all x, y ∈ C, the mapping F of [0, 1] into E*, defined by F(t) = B(tx + (1 - t)y), is continuous with respect to the weak* topology of E*. We define by N _C (v) the normal cone for C at a point v ∈ C, that is,

$$N_C\left(v\right)=\left\{x^{*}\in E^{*}:⟨v-y,x^{*}⟩\ge 0,\forall y\in C\right\}.$$

(2.9)

Theorem 2.9. (Rockafellar [18]) Let C be a nonempty, closed convex subset of a Banach space E and B a monotone, hemicontinuous operator of C into E*. Let T ⊂ E × E* be an operator defined as follows:

$$Tv=\left\{\begin{array}{c}Bv+N_C\left(v\right),v\in C;\hfill \\ \cancel{0},\text{otherwise}.\hfill \end{array}\right.$$

(2.10)

Then T is maximal monotone and T^-10 = V I(C, B).

Lemma 2.10. (Tan and Xu [35]) Let {a _n } and {b _n } be two sequence of nonnegative real numbers satisfying the inequality

$$a_{n+1}=a_n+b_{n}foralln\ge 0.$$

If ${\sum }_{n=1}^{\infty }{b}_n<\infty$, then lim_n→∞a _n exists.

Lemma 2.11. (Xu [36]) Let {s _n } be a sequence of nonnegative real numbers satisfying

$$s_{n+1}=\left(1-{\alpha }_n\right)s_n+{\alpha }_n{t}_n+r_{n}n\ge 1,$$

where {α _n }, {t _n }, and {r _n } satisfy {α _n } ⊂ [0, 1], ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$, lim sup_n→∞t _n ≤ 0 and r _n ≥ 0, ${\sum }_{n=1}^{\infty }{r}_n<\infty$. Then lim_n→∞s _n = 0.

For solving the mixed equilibrium problem, let us assume that the bifunction Θ: C × C → ℝ and φ: C → ℝ is convex and lower semi-continuous satisfies the following conditions:

(A1) Θ(x, x) = 0 for all x ∈ C;

(A2) Θ is monotone, i.e., Θ(x, y) + Θ(y, x) ≤ 0 for all x, y ∈ C;

(A3) for each x, y, z ∈ C,

$$\underset{t\downarrow 0}{\text{lim}\text{sup}}\Theta \left(tz+\left(1-t\right)x,y\right)\le \Theta \left(x,y\right);$$

(A4) for each x ∈ C, y ↦ Θ(x, y) is convex and lower semi-continuous.

Lemma 2.12. (Blum and Oettli [7]) Let C be a closed convex subset of a uniformly smooth, strictly convex and reflexive Banach space E and let Θ be a bifunction of C × C into ℝ satisfying (A 1)-(A 4). Let r > 0 and x ∈ E. Then, there exists z ∈ C such that

$$\Theta \left(z,y\right)+\frac{1}{r}⟨y-z,z-x⟩\ge 0forally\in C.$$

Lemma 2.13. (Takahashi and Zembayashi [37]) Let C be a closed convex subset of a uniformly smooth, strictly convex and reflexive Banach space E and let Θ be a bifunction from C × C to ℝ satisfying (A 1)-(A 4). For all r > 0 and x ∈ E, define a mapping T _r : E → C as follows:

$$T_{r}x=\left\{z\in C:\Theta \left(z,y\right)+\frac{1}{r}⟨y-z,Jz-Jx⟩\ge 0,\forall y\in C\right\}$$

(2.11)

for all x ∈ E. Then, the followings hold:

• (1) T _r is single-valued;

• (2) T _r is a firmly nonexpansive-type mapping, i.e., for all x, y ∈ E,

  $$⟨T_{r}x-T_{r}y,J{T}_{r}x-J{T}_{r}y⟩\le ⟨T_{r}x-T_{r}y,Jx-Jy⟩;$$

• (3) F(T _r ) = EP(Θ);

• (4) EP(Θ) is closed and convex.

Lemma 2.14. (Takahashi and Zembayashi [37]) Let C be a closed convex subset of a smooth, strictly convex, and reflexive Banach space E, let Θ be a bifunction from C ×C to ℝ satisfying (A 1)-(A 4) and let r > 0. Then, for x ∈ E and q ∈ F(T _r ),

$$\varphi \left(q,T_{r}x\right)+\varphi \left(T_{r}x,x\right)\le \varphi \left(q,x\right).$$

Lemma 2.15. (Zhang [24]) Let C be a closed convex subset of a smooth, strictly convex and reflexive Banach space E. Let B: C → E* be a continuous and monotone mapping, φ: C → ℝ is convex and lower semi-continuous and Θ be a bifunction from C × C to ℝ satisfying (A1)-(A4). For r > 0 and x ∈ E, then there exists u ∈ C such that

$$\Theta \left(u,y\right)+⟨Bu,y-u⟩+\phi \left(y\right)-\phi \left(u\right)+\frac{1}{r}⟨y-u,Ju-Jx⟩\ge 0,\forall y\in C.$$

Define a mapping K _r : C → C as follows:

$$K_r\left(x\right)=\left\{u\in C:\Theta \left(u,y\right)+⟨Bu,y-u⟩+\phi \left(y\right)-\phi \left(u\right)+\frac{1}{r}⟨y-u,Ju-Jx⟩\ge 0,\forall y\in C\right\}$$

(2.12)

for all x ∈ E. Then, the followings hold:

• (i) K _r is single-valued;

• (ii) K _r is firmly nonexpansive, i.e., for all x, y ∈ E, 〈K _r x - K _r y, JK _r x - JK _r y〉 ≤ 〈K _r x -K _r y, Jx -Jy〉;

• (iii) F(K _r ) = Ω;

• (iv) Ω is closed and convex;

• (v) ϕ(p, K _r z) + ϕ(K _r z, z) ≤ ϕ(p, z) ∀p ∈ F(K _r ), z ∈ E.

Remark 2.16. (Zhang [24]) It follows from Lemma 2.13 that the mapping K _r : C → C defined by (2.12) is a relatively nonexpansive mapping. Thus, it is quasi-ϕ-nonexpansive.

Lemma 2.17. (Xu [31] and Zalinescu [32]) Let E be a uniformly convex Banach space and let r > 0. Then there exists a strictly increasing, continuous and convex function g: [0, ∞) → [0, ∞) such that g(0) = 0 and

$${∥tx+\left(1-t\right)y∥}^2\le t{∥x∥}^2+\left(1-t\right){∥y∥}^2-t\left(1-t\right)g\left(∥x-y∥\right)$$

(2.13)

for all x, y ∈ B _r (0) and t ∈ [0, 1], where B _r (0) = {z ∈ E: ||z|| ≤ r}.

3. Strong convergence theorem

In this section, we prove a strong convergence theorem for finding a common element of the set of solutions of mixed equilibrium problems, the set of solution of the variational inequality problem, the fixed point set of relatively nonexpansive mappings and the zero point of a maximal monotone operators in a Banach space by using the shrinking hybrid projection method.

Theorem 3.1. Let E be a 2-uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E. Let Θ be a bifunction from C × C to ℝ satisfying (A1)-(A4) let φ: C → ℝ be a proper lower semicontinuous and convex function, let T: E → E* be a maximal monotone operator satisfying D(T) ⊂ C. Let J _r = (J + rT)^-1J for r > 0, let B: C → E* be a continuous and monotone mappings and S be a relatively nonexpansive mappings from C into itself, with $F:=\Omega \cap VI\left(C,A\right)\cap T^{-1}\left(0\right)\cap F\left(S\right)\ne \cancel{0}$. Assume that A an operator of C into E* that satisfies the conditions (C1)-(C3). Let {x _n } be a sequence generated by x₁ = x ∈C and,

$$\left\{\begin{array}{c}{u}_n=K_{r_n}{x}_n,\hfill \\ z_n={\Pi }_C{J}^{-1}\left(J-{\lambda }_{n}A\right)u_n,\hfill \\ y_n=J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{J}_{r_n}{z}_n\right),\hfill \\ x_{n+1}={\Pi }_C{J}^{-1}\left({\alpha }_{n}Jx+\left(1-{\alpha }_n\right)J{y}_n\right),\hfill \end{array}\right.$$

(3.1)

for all n ∈ ℕ, where Π _C is the generalized projection from E onto C, J is the duality mapping on E. The coefficient sequences {λ _n } ⊂ [a, b] for some a, b with $0<a<b<\frac{c^2\alpha }{2},\frac{1}{c}$ is the 2-uniformly convexity constant of E and {α _n } ⊂ [0, 1], {β _n } ⊂ (0, 1] {r _n } ⊂ (0, ∞) satisfying

• (i) lim_n→∞α _n = 0, ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$,

• (ii) lim sup_n→∞β _n < 1,

• (iii) lim inf_n→∞r _n > 0.

Then the sequence {x _n } converges strongly to Π _F x₀.

Proof . Let H(u _n , y) = Θ(u _n , y) + 〈Bu _n , y -u _n 〉 + φ(y) - φ(u _n ), y ∈ C and $K_{r_n}=\left\{u_n\in C:H\left(u_n,y\right)+\frac{1}{r_n}⟨y-u_n,J{u}_n-J{x}_n⟩\ge 0,\forall y\in C\right\}$. We first show that {x _n } is bounded. Put v _n = J^-1(J - λ _n A)u _n and $w_n=J_{r_n}{z}_n$ for all n ≥ 0. Let p ∈ F: = Ω ∩ V I(C, A) ∩ T^-1(0) ∩ F(S) and $u_n=K_{r_n}{x}_n$. Since S, $J_{r_n}$ and $K_{r_n}$ are relatively nonexpansive mappings, we get

$$\varphi \left(p,u_n\right)=\varphi \left(p,K_{r_n}{x}_n\right)\le \varphi \left(p,x_n\right)$$

(3.2)

and Lemma 2.7, the convexity of the function V in the second variable, we obtain

$$\begin{array}{cc}\hfill \varphi \left(p,z_n\right)& =\varphi \left(p,{\Pi }_C{v}_n\right)\hfill \\ \le \varphi \left(p,v_n\right)=\varphi \left(p,J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)\right)\hfill \\ \le V\left(p,J{u}_n-{\lambda }_{n}A{u}_n+{\lambda }_{n}A{u}_n\right)-2⟨J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-p,{\lambda }_{n}A{u}_n⟩\hfill \\ =V\left(p,J{u}_n\right)-2{\lambda }_n⟨v_n-p,A{u}_n⟩\hfill \\ =\varphi \left(p,u_n\right)-2{\lambda }_n⟨u_n-p,A{u}_n⟩+2⟨v_n-u_n,-{\lambda }_{n}A{u}_n⟩.\hfill \end{array}$$

(3.3)

Since p ∈ V I(C, A) and A is α-inverse-strongly monotone, we have

$$\begin{array}{cc}\hfill -2{\lambda }_n⟨u_n-p,A{u}_n⟩& =-2{\lambda }_n⟨u_n-p,A{u}_n-Ap⟩-2{\lambda }_n⟨u_n-p,Ap⟩\hfill \\ \le -2\alpha {\lambda }_n{∥A{u}_n-Ap∥}^2,\hfill \end{array}$$

(3.4)

and by Lemma 2.1, we obtain

$$\begin{array}{cc}\hfill 2⟨v_n-u_n,-{\lambda }_{n}A{u}_n⟩& =2⟨J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-u_n,-{\lambda }_{n}A{u}_n⟩\hfill \\ \le 2∥J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-u_n∥∥{\lambda }_{n}A{u}_n∥\hfill \\ \le \frac{4}{c^2}∥J{u}_n-{\lambda }_{n}A{u}_n-J{u}_n∥∥{\lambda }_{n}A{u}_n∥\hfill \\ =\frac{4}{c^2}{\lambda }_n^2{∥A{u}_n∥}^2\hfill \\ \le \frac{4}{c^2}{\lambda }_n^2{∥A{u}_n-Ap∥}^2.\hfill \end{array}$$

(3.5)

Substituting (3.4) and (3.5) into (3.3), we get

$$\begin{array}{cc}\hfill \varphi \left(p,z_n\right)& \le \varphi \left(p,u_n\right)-2\alpha {\lambda }_n{∥A{u}_n-Ap∥}^2+\frac{4}{c^2}{\lambda }_n^2{∥A{u}_n-Ap∥}^2\hfill \\ \le \varphi \left(p,u_n\right)+2{\lambda }_n\left(\frac{2}{c^2}{\lambda }_n-\alpha \right){∥A{u}_n-Ap∥}^2\hfill \\ \le \varphi \left(p,u_n\right)\hfill \\ \le \varphi \left(p,x_n\right).\hfill \end{array}$$

(3.6)

By Lemmas 2.7, 2.8 and (3.6), we have

$$\begin{array}{cc}\hfill \varphi \left(p,y_n\right)& =\varphi \left(p,J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{w}_n\right)\right)\hfill \\ =V\left(p,{\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{w}_n\right)\hfill \\ \le V\left(p,{\beta }_{n}J{x}_n\right)+\left(1-{\beta }_n\right)V\left(p,JS{w}_n\right)\hfill \\ ={\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(p,S{w}_n\right)\hfill \\ \le {\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(p,w_n\right)\hfill \\ \le {\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\left(\varphi \left(p,z_n\right)-\varphi \left(w_n,z_n\right)\right)\hfill \\ \le {\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(p,z_n\right)\hfill \\ \le {\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(p,x_n\right)\hfill \\ =\varphi \left(p,x_n\right),\hfill \end{array}$$

(3.7)

it follows that

$$\begin{array}{cc}\hfill \varphi \left(p,x_{n+1}\right)& =\varphi \left(p,{\Pi }_C{J}^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right)\right)\hfill \\ \le \varphi \left(p,J^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right)\right)\hfill \\ =V\left(p,{\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right)\hfill \\ \le {\alpha }_{n}V\left(p,J{x}_1\right)+\left(1-{\alpha }_n\right)V\left(p,J{y}_n\right)\hfill \\ ={\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,y_n\right)\hfill \\ \le {\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,x_n\right)\hfill \end{array}$$

(3.8)

for all n ∈ ℕ. Hence, by induction, we have that ϕ(p, x _n ) ≤ ϕ(p, x₁) for all n ∈ ℕ. Since (||x _n || - ||p||)² ≤ ϕ(p, x _n ). It implies that {x _n } is bounded and {y _n }, {z _n }, {w _n } are also bounded.

From (3.6)-(3.8), we have

$$\begin{array}{cc}\hfill \varphi \left(p,x_{n+1}\right)& \le {\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\left[{\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\left(\varphi \left(p,x_n\right)-\varphi \left(w_n,z_n\right)\right)\right]\hfill \\ \le {\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,x_n\right)-\left(1-{\alpha }_n\right)\left(1-{\beta }_n\right)\varphi \left(w_n,z_n\right)\hfill \end{array}$$

and then

$$\left(1-{\alpha }_n\right)\left(1-{\beta }_n\right)\varphi \left(w_n,z_n\right)\le {\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,x_n\right)-\varphi \left(p,x_{n+1}\right)$$

for all n ∈ ℕ. Since lim_n-∞α _n = 0, lim sup_n→∞β _n < 1, it follows that lim_n→∞ϕ(w _n , z _n ) = 0. Applying Lemma 2.4, we have

$$\underset{n\to \infty }{\text{lim}}∥w_n-z_n∥=\underset{n\to \infty }{\text{lim}}∥J_{r_n}{z}_n-z_n∥=0.$$

(3.9)

Since J is uniformly norm-to-norm continuous on bounded sets, we obtain

$$\underset{n\to \infty }{\text{lim}}∥J{w}_n-J{z}_n∥=\underset{n\to \infty }{\text{lim}}∥J{J}_{r_n}{z}_n-J{z}_n∥=0.$$

(3.10)

By (3.2), (3.6)-(3.8) again, we note that

$$\begin{array}{cc}\hfill \varphi \left(p,x_{n+1}\right)& \le {\alpha }_n\varphi \left(p,x_1\right)+\hfill \\ \left(1-{\alpha }_n\right)\left\{{\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\left[\varphi \left(p,x_n\right)-2{\lambda }_n\left(\alpha -\frac{2}{c^2}{\lambda }_n\right){∥A{u}_n-Ap∥}^2\right]\right\}\hfill \\ \le {\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,x_n\right)-\left(1-{\alpha }_n\right)\left(1-{\beta }_n\right)2{\lambda }_n\left(\alpha -\frac{2}{c^2}{\lambda }_n\right){∥A{u}_n-Ap∥}^2\hfill \end{array}$$

and hence

$$2{\lambda }_n\left(\alpha -\frac{2}{c^2}{\lambda }_n\right){∥A{u}_n-Ap∥}^2\le \frac{1}{\left(1-{\alpha }_n\right)\left(1-{\beta }_n\right)}\left({\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,x_n\right)-\varphi \left(p,x_{n+1}\right)\right)$$

for all n ∈ ℕ. Since $0<a\le {\lambda }_n\le b<\frac{c^2\alpha }{2}$, lim_n→∞α _n = 0, lim sup_n→∞β _n < 1, we have

$$\underset{n\to \infty }{\text{lim}}∥A{u}_n-Ap∥=0.$$

(3.11)

From Lemmas 2.6, 2.7 and (3.5), we get

$$\begin{array}{cc}\hfill \varphi \left(u_n,z_n\right)=\varphi \left(u_n,{\Pi }_C{v}_n\right)& \le \varphi \left(u_n,v_n\right)\hfill \\ =\varphi \left(u_n,J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)\right)\hfill \\ =V\left(u_n,J{u}_n-{\lambda }_{n}A{u}_n\right)\hfill \\ \le V\left(u_n,\left(J{u}_n-{\lambda }_{n}A{u}_n\right)+{\lambda }_{n}A{u}_n\right)\hfill \\ -2⟨J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-u_n,{\lambda }_{n}A{u}_n⟩\hfill \\ =\varphi \left(u_n,u_n\right)+2⟨v_n-u_n,-{\lambda }_{n}A{u}_n⟩\hfill \\ =2⟨v_n-u_n,-{\lambda }_{n}A{u}_n⟩\hfill \\ \le \frac{4}{c^2}{\lambda }_n^2{∥A{u}_n-Ap∥}^2.\hfill \end{array}$$

From Lemma 2.4 and (3.11), we have

$$\underset{n\to \infty }{\text{lim}}∥u_n-z_n∥=0.$$

(3.12)

Since J is uniformly norm-to-norm continuous on bounded sets, we obtain

$$\underset{n\to \infty }{\text{lim}}∥J{u}_n-J{z}_n∥=0.$$

(3.13)

From Lemmas 2.6, 2.7 and (3.5), we obtain

$$\begin{array}{cc}\hfill \varphi \left(x_n,z_n\right)& =\varphi \left(x_n,{\Pi }_C{J}^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)\right)\hfill \\ \le \varphi \left(x_n,J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)\right)\hfill \\ =V\left(x_n,J{u}_n-{\lambda }_{n}A{u}_n\right)\hfill \\ \le V\left(x_n,\left(J{u}_n-{\lambda }_{n}A{u}_n\right)+{\lambda }_{n}A{u}_n\right)-2⟨J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-u_n,{\lambda }_{n}A{u}_n⟩\hfill \\ =\varphi \left(x_n,u_n\right)+2⟨J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-u_n,-{\lambda }_{n}A{u}_n⟩\hfill \\ =\varphi \left(x_n,x_n\right)+2⟨J^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right)-u_n,-{\lambda }_{n}A{u}_n⟩\hfill \\ =\frac{4}{c^2}{∥A{u}_n-Ap∥}^2\hfill \end{array}$$

for all n ∈ ℕ. Since lim_n→∞||Au _n - Ap ||² = 0, we have lim_n→∞ϕ(x _n , z _n ) = 0.

Applying Lemma 2.4, we get

$$\underset{n\to \infty }{\text{lim}}∥x_n-z_n∥=0.$$

(3.14)

Since J is uniformly norm-to-norm continuous on bounded set, we obtain

$$\underset{n\to \infty }{\text{lim}}∥J{x}_n-J{z}_n∥=0.$$

(3.15)

So, by the triangle inequality, we get

$$∥x_n-u_n∥\le ∥x_n-z_n∥+∥z_n-u_n∥.$$

By (3.12) and (3.14), we also have

$$\underset{n\to \infty }{\text{lim}}∥x_n-u_n∥=0.$$

(3.16)

From (3.1), we obtain

$$\begin{array}{cc}\hfill \varphi \left(y_n,z_n\right)& =\varphi \left(x_n,J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{w}_n\right)\right)\hfill \\ =V\left(x_n,{\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{w}_n\right)\hfill \\ \le {\beta }_{n}V\left(x_n,J{x}_n\right)+\left(1-{\beta }_n\right)V\left(x_n,JS{w}_n\right)\hfill \\ ={\beta }_n\varphi \left(x_n,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(x_n,S{w}_n\right)\hfill \\ \le {\beta }_n\varphi \left(x_n,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(x_n,w_n\right)\hfill \\ =\left(1-{\beta }_n\right)\varphi \left(x_n,z_n\right)\hfill \end{array}$$

for all n ∈ ℕ. Since lim _n→∞ ϕ(x _n , z _n ) = 0, we have lim_n→∞ϕ(y _n , z _n ) = 0. Applying Lemma 2.4, we get

$$\underset{n\to \infty }{\text{lim}}∥y_n-z_n∥=0.$$

(3.17)

Since J is uniformly norm-to-norm continuous on bounded set, we obtain

$$\underset{n\to \infty }{\text{lim}}∥J{y}_n-J{z}_n∥=0.$$

(3.18)

From

$$∥x_n-y_n∥\le ∥x_n-z_n∥+∥z_n-y_n∥,$$

we have

$$\underset{n\to \infty }{\text{lim}}∥x_n-y_n∥=0.$$

(3.19)

Since J is uniformly norm-to-norm continuous on bounded set, we obtain

$$\underset{n\to \infty }{\text{lim}}∥J{x}_n-J{y}_n∥=0.$$

(3.20)

From Lemma 2.17 and (3.7), we have

$$\begin{array}{cc}\hfill \varphi \left(p,y_n\right)& =\varphi \left(p,J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{w}_n\right)\right)\hfill \\ ={∥p∥}^2-2⟨p{\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{w}_n⟩+{∥\beta J{x}_n+\left(1-{\beta }_n\right)JS{w}_n∥}^2\hfill \\ \le {∥p∥}^2-2{\beta }_n⟨p,J{x}_n⟩-2\left(1-{\beta }_n\right)⟨p,JS{w}_n⟩+{\beta }_n{∥x_n∥}^2+\left(1-{\beta }_n\right){∥S{w}_n∥}^2\hfill \\ -{\beta }_n\left(1-{\beta }_n\right)g\left(∥J{x}_n-JS{w}_n∥\right)\hfill \\ ={\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(p,S{w}_n\right)-{\beta }_n\left(1-{\beta }_n\right)g\left(∥J{x}_n-JS{w}_n∥\right)\hfill \\ \le {\beta }_n\varphi \left(p,x_n\right)+\left(1-{\beta }_n\right)\varphi \left(p,x_n\right)-{\beta }_n\left(1-{\beta }_n\right)g\left(∥J{x}_n-JS{w}_n∥\right)\hfill \\ =\varphi \left(p,x_n\right)-{\beta }_n\left(1-{\beta }_n\right)g\left(∥J{x}_n-JS{w}_n∥\right).\hfill \end{array}$$

(3.21)

This implies that

$${\beta }_n\left(1-{\beta }_n\right)g\left(∥J{x}_n-JS{w}_n∥\right)\le \varphi \left(p,x_n\right)-\varphi \left(p,y_n\right).$$

(3.22)

On the other hand, we have

$$\begin{array}{cc}\hfill \varphi \left(p,x_n\right)-\varphi \left(p,y_n\right)& ={∥x_n∥}^2-{∥y_n∥}^2-2⟨p,J{x}_n-J{y}_n⟩\hfill \\ =∥x_n-y_n∥\left(∥x_n∥+∥y_n∥\right)+2∥p∥∥J{x}_n-J{y}_n∥.\hfill \end{array}$$

(3.23)

Noticing (3.19) and (3.20), we obtain

$$\varphi \left(p,x_n\right)-\varphi \left(p,y_n\right)\to 0,\text{as }n\to \infty .$$

(3.24)

Since lim sup_n→∞β _n < 1 and (3.24), it follows from (3.22) that

$$g\left(∥J{x}_n-JS{w}_n∥\right)\to 0,\text{as}n\to \infty .$$

(3.25)

If follows from the property of g that

$$\underset{n\to \infty }{\text{lim}}∥J{x}_n-JS{w}_n∥=0.$$

(3.26)

Since J is uniformly norm-to-norm continuous on bounded set, we see that

$$\underset{n\to \infty }{\text{lim}}∥x_n-S{w}_n∥=0.$$

(3.27)

Since

$$∥z_n-S{w}_n∥\le ∥z_n-x_n∥+∥x_n-S{w}_n∥,$$

from (3.14) and (3.27), we obtain that

$$\underset{n\to \infty }{\text{lim}}∥z_n-S{w}_n∥=0.$$

(3.28)

By (3.9) and (3.14), we obtain

$$\underset{n\to \infty }{\text{lim}}∥w_n-x_n∥=0.$$

(3.29)

Also, by (3.9) and (3.28), we obtain

$$\underset{n\to \infty }{\text{lim}}∥w_n-S{w}_n∥=0.$$

(3.30)

Since {x _n } is bounded, there exists a subsequence $\left\{x_{n_i}\right\}$ of {x _n } such that $x_{n_i}\rightharpoonup u\in C$. It follows from (3.29), we have $w_{n_i}\rightharpoonup u$ as i → ∞ and S be a relatively nonexpansive, we have that $u\in \hat{F}\left(S\right)=F\left(S\right)$.

Next, we show that u ∈ T^-10. Indeed, since lim inf_n→∞r _n > 0, it follows from (3.10) that

$$\underset{n\to \infty }{\text{lim}}\left|\right|A_{r_n}{z}_n\left|\right|=\underset{n\to \infty }{\text{lim}}\frac{1}{r_n}\left|\right|J{z}_n-J{w}_n\left|\right|=0.$$

(3.31)

If (z, z*) ∈ T, then it holds from the monotonicity of A that

$$⟨z-z_{n_i},z^{*}-A_{r_{n_i}}{z}_{n_i}⟩\ge 0$$

for all i ∈ ℕ. Letting i → ∞, we get 〈 z - u, z*〉 ≥ 0. Then, the maximality of T implies u ∈ T^-10.

Next, we show that u ∈ V I(C, A). Let B ⊂ E × E* be an operator as follows:

$$Bv=\left\{\begin{array}{c}Av+N_C\left(v\right),v\in C;\hfill \\ \cancel{0},\text{otherwise}\hfill \end{array}\right.$$

By Theorem 2.9, B is maximal monotone and B^-10 = V I(C, A). Let (v, w) ∈ G(B).

Since w ∈ Bv = Av + N _C (v), we get w - Av ∈ N _C (v). From z _n ∈ C, we have

$$⟨v-z_n,w-Av⟩\ge 0.$$

(3.32)

On the other hand, since z _n = Π _C J^-1 (Ju _n - λ _n Au _n ). Then by Lemma 2.5, we have

$$⟨v-z_n,J{z}_n-\left(J{u}_n-{\lambda }_{n}A{u}_n\right)⟩\ge 0,$$

thus

$$⟨v-z_n,\frac{J{u}_n-J{z}_n}{{\lambda }_n}-Au{x}_n⟩\le 0.$$

(3.33)

It follows from (3.32) and (3.33) that

$$\begin{array}{cc}\hfill ⟨v-z_n,w⟩& \ge ⟨v-z_n,Av⟩\hfill \\ \ge ⟨v-z_n,Av⟩+⟨v-z_n,\frac{J{u}_n-J{z}_n}{{\lambda }_n}-A{u}_n⟩\hfill \\ =⟨v-z_n,Av-A{u}_n⟩+⟨v-z_n,\frac{J{u}_n-J{z}_n}{{\lambda }_n}⟩\hfill \\ =⟨v-z_n,Av-A{z}_n⟩+⟨v-z_n,A{z}_n-A{u}_n⟩+⟨v-z_n,\frac{J{u}_n-J{z}_n}{{\lambda }_n}⟩\hfill \\ \ge -∥v-z_n∥\frac{∥z_n-u_n∥}{\alpha }-∥v-z_n∥\frac{∥J{u}_n-J{z}_n∥}{a}\hfill \\ \ge -M\left(\frac{∥z_n-u_n∥}{\alpha }+\frac{∥J{u}_n-J{z}_n∥}{a}\right),\hfill \end{array}$$

where M = sup_n≥1{||v - z _n ||}. From (3.12) and (3.13), we obtain 〈v - u, w〉 ≥ 0. By the maximality of B, we have u ∈ B^-10 and hence u ∈ V I(C, A).

Next, we show that u ∈ Ω. From (3.16) and J is uniformly norm-to-norm continuous on bounded set, we obtain

$$\underset{n\to \infty }{\text{lim}}∥J{u}_n-J{x}_n∥=0.$$

(3.34)

From the assumption lim inf_n→∞r _n > a, we get

$$\underset{n\to \infty }{\text{lim}}\frac{∥J{u}_n-J{x}_n∥}{r_n}=0.$$

Noticing that $u_n=K_{r_n}{x}_n$, we have

$$H\left(u_n,y\right)+\frac{1}{r_n}⟨y-u_n,J{u}_n-J{x}_n⟩\ge 0,\forall y\in C.$$

Hence,

$$H\left(u_{n_i},y\right)+\frac{1}{r_{n_i}}⟨y-u_{n_i},J{u}_{n_i}-J{x}_{n_i}⟩\ge 0,\forall y\in C.$$

From the (A2), we note that

$$∥y-u_{n_i}∥\frac{∥J{u}_{n_i}-J{x}_{n_i}∥}{r_{n_i}}\ge \frac{1}{r_{n_i}}⟨y-u_{n_i},J{u}_{n_i}-J{x}_{n_i}⟩\ge -H\left(u_{n_i},y\right)\ge H\left(y,u_{n_i}\right),\forall y\in C.$$

Taking the limit as n → ∞ in above inequality and from (A4) and $u_{n_i}\rightharpoonup u$, we have H(y, u) ≤ 0, ∀y ∈ C. For 0 < t < 1 and y ∈ C, define y _t = ty + (1 - t)u. Noticing that y, u ∈ C, we obtains y _t ∈ C, which yields that H(y _t , u) ≤ 0. It follows from (A1) that

$$0=H\left(y_t,y_t\right)\le tH\left(y_t,y\right)+\left(1-t\right)H\left(y_t,\widehat{x}\right)\le tH\left(y_t,y\right).$$

That is, H(y _t , y) ≥ 0.

Let t ↓ 0, from (A3), we obtain H(u, y) ≥ 0, ∀y ∈ C. This implies that u ∈ Ω. Hence u ∈ F: = Ω ∩ V I(C, B) ∩ T^-1(0).

Finally, we show that u = Π _F x. Indeed from $x_n={\Pi }_{C_n}x$ and Lemma 2.5, we have

$$⟨Jx-J{x}_n,x_n-z⟩\ge 0,\forall z\in C_n.$$

Since F ⊂ C _n , we also have

$$⟨Jx-J{x}_n,x_n-p⟩\ge 0,\forall p\in F.$$

(3.35)

Taking limit n → ∞, we obtain

$$⟨Jx-Ju,u-p⟩\ge 0,\forall p\in F.$$

By again Lemma 2.5, we can conclude that u = Π _F x₀. This completes the proof. □

Corollary 3.2. Let E be a 2-uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E. Let T: E → E* be a maximal monotone operator satisfying D(T) ⊂ C. Let J _r = (J + rT)^-1 J for r > 0, let A be an α-inverse-strongly monotone operator of C into E* and S be a relatively nonexpansive mappings from C into itself, with $F:=VI\left(C,A\right)\cap T^{-1}\left(0\right)\cap F\left(S\right)\ne \cancel{0}$. Assume that A an operator of C into E* that satisfies the conditions (C1)-(C3). Let {x _n } be a sequence generated by x₁ = x ∈ C and,

$$\left\{\begin{array}{c}{z}_n={\Pi }_C{J}^{-1}\left(J{x}_n-{\lambda }_{n}A{x}_n\right),\hfill \\ y_n=J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{J}_{r_n}{z}_n\right),\hfill \\ x_{n+1}={\Pi }_C{J}^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right),\hfill \end{array}\right.$$

(3.36)

for all n ∈ ℕ, where Π _C is the generalized projection from E onto C, J is the duality mapping on E. The coefficient sequence {a _n } ⊂ [0, 1], {β _n } ⊂ (0, 1], {r _n } ⊂ (0, ∞) satisfying lim_n→∞α _n = 0, ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$, lim sup_n→∞β _n < 1, lim inf_n→∞r _n > 0 and {λ _n } ⊂ [a, b] for some a, b with $0<a<b<\frac{c^2\alpha }{2}$, $\frac{1}{c}$ is the 2-uniformly convexity constant of E. Then the sequence {x _n } converges strongly to Π _F x₀.

4. Weak convergence theorem

We next prove a weak convergence theorem under difference condition on data. First we prove the generalized projection sequence {Π _F x₀} of {x _n } is strongly convergent.

Theorem 4.1. Let E be a 2-uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E. Let Θ be a bifunction from C × C to ℝ satisfying (A1)-(A4) let φ: C → ℝ be a proper lower semicontinuous and convex function, let T: E → E* be a maximal monotone operator satisfying D(T) ⊂ C. Let J _r = (J + rT)^-1 J for r > 0 and let A be an α-inverse-strongly monotone operator of C into E*, let B: C → E* be a continuous and monotone mappings and S be a relatively nonexpansive mapping. from C into itself, with $F:=\Omega \cap VI\left(C,A\right)\cap T^{-1}\left(0\right)\cap F\left(S\right)\ne \cancel{0}$. Assume that A an operator of C into E* that satisfies the conditions (C1)-(C3). Let {x _n } be a sequence generated by x₁ = x ∈ C and,

$$\left\{\begin{array}{c}{u}_n=K_{r_n}{x}_n,\hfill \\ z_n={\Pi }_C{J}^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right),\hfill \\ y_n=J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{J}_{r_n}{z}_n\right),\hfill \\ x_{n+1}={\Pi }_C{J}^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right),\hfill \end{array}\right.$$

(4.1)

for all n ∈ ℕ, where Π _C is the generalized projection from E onto C, J is the duality mapping on E. The coefficient sequence {α _n } ⊂ [0, 1], {β _n } ⊂ (0, 1], {r _n } ⊂ (0, ∞) satisfying ${\sum }_{n=1}^{\infty }{\alpha }_n<\infty$, lim sup_n→∞β _n < 1, lim inf_n→∞r _n > 0 and {λ _n } ⊂ [a, b] for some a, b with $0<a\le {\lambda }_n\le b<\frac{c^2\alpha }{2}$ , $\frac{1}{c}$ is the 2-uniformly convexity constant of E. Then the sequence {Π _F x _n } converges strongly to an element v of F , which is a unique element of F satisfying

$$\underset{n\to \infty }{\text{lim}}\varphi \left(v,x_n\right)=\underset{y\in F}{\text{min}}\underset{n\to \infty }{\text{lim}}\varphi \left(y,x_n\right).$$

Proof . Let H(u _n , y) = Θ(u _n , y) + 〈Bu _n , y - u _n 〉 + φ(y) - φ(u _n ), y ∈ C and $K_{r_n}=\left\{u_n\in C:H\left(u_n,y\right)+\frac{1}{r_n}⟨y-u_n,J{u}_n-J{x}_n⟩\ge 0.\forall y\in C\right\}$. We first show that {x _n } is bounded. Let p ∈ F: = Ω ∩ V I(C, A) ∩ T^-1(0) ∩ F (S) and $u_n=K_{r_n}{x}_n$. Put v _n = J^-1(Ju _n - λ _n Au _n ) and $w_n=J_{r_n}{z}_n$ for all n ≥ 0. Since $J_{r_n}$, $K_{r_n}$ and S are relatively nonexpansive mappings. By (3.8), we have that, for all n ∈ ℕ

$$\varphi \left(p,x_{n+1}\right)\le {\alpha }_n\varphi \left(p,x_1\right)+\left(1-{\alpha }_n\right)\varphi \left(p,x_n\right).$$

(4.2)

From ${\sum }_{n=1}^{\infty }{\alpha }_n<\infty$ and Lemma 2.10, we deduce that lim_n→∞ϕ(p, x _n ) exists. This implies that {ϕ(p, x _n )} is bounded. So {x _n } is bounded.

Define a function g: F → [0, ∞) as follows:

$$g\left(p\right)=\underset{n\to \infty }{\text{lim}}\varphi \left(p,x_n\right),\forall p\in F.$$

Then, by the same argument as in proof of [[22], Theorem 3.1], we obtain g is a continuous convex function and if ||z _n || → ∞ then g(z _n ) → ∞. Hence, by [[28], Theorem 1.3.11], there exists a point v ∈ F such that

$$g\left(v\right)=\underset{y\in F}{\text{min}}g\left(y\right)\left(:=l\right).$$

(4.3)

Put t _n = Π _F x _n for all n ≥ 0. We next prove that t _n → v as n → ∞. Suppose on the contrary that there exists ε₀ > 0 such that, for each n ∈ ℕ, there is n' ≥ n satisfying ||w_n'- v|| ≥ ϵ₀. Since v ∈ F, we have

$$\varphi \left(t_n,x_n\right)=\varphi \left({\Pi }_F{x}_n,x_n\right)\le \varphi \left(v,{\Pi }_F{x}_n\right)+\varphi \left({\Pi }_F{x}_n,x_n\right)\le \varphi \left(v,x_n\right)$$

(4.4)

for all n ≥ 0. This implies that

$$\underset{n\to \infty }{\text{lim}\text{sup}}\varphi \left(t_n,x_n\right)\le \underset{n\to \infty }{\text{lim}}\varphi \left(v,x_n\right)=l.$$

(4.5)

Since (||v|| - ||Π _F x _n ||)² ≤ ϕ(v, w _n ) ≤ ϕ(v, x _n ) for all n ≥ 0 and {x _n } is bounded, we get {w _n } is also bounded. By Lemma 2.3, there exists a stricly increasing, continuous and convex function K: [0, ∞) → [0, ∞) such that K(0) = 0 and

$${∥\frac{w_n+v}{2}∥}^2\le \frac{1}{2}{∥t_n∥}^2+\frac{1}{2}{∥v∥}^2-\frac{1}{4}K\left(∥t_n-v∥\right),$$

(4.6)

for all n ≥ 0. Now, choose σ satisfying $0<\sigma <\frac{1}{4}K\left({ϵ}_0\right)$. Hence, there exists n₀ ∈ ℕ such that

$$\varphi \left(t_n,x_n\right)\le l+\sigma ,\varphi \left(v,x_n\right)\le l+\sigma ,$$

(4.7)

for all n ≥ 0. Thus there exists k ≥ n₀ satisfying the following:

$$\varphi \left(t_k,x_k\right)\le l+\sigma ,\varphi \left(v,x_k\right)\le l+\sigma ,∥t_k-v∥\ge {ϵ}_0.$$

(4.8)

From (4.2), (4.6) and (4.8), we obtain

$$\begin{array}{cc}\hfill \varphi \left(\frac{t_k+v}{2},x_{n+k}\right)& \le \varphi \left(\frac{t_k+v}{2},x_k\right)\hfill \\ ={∥\frac{t_k+v}{2}∥}^2-2⟨\frac{t_k+v}{2},J{x}_k⟩+{∥x_k∥}^2\hfill \\ \le \frac{1}{2}{∥t_k∥}^2+\frac{1}{2}{∥v∥}^2-\frac{1}{4}K\left(∥t_k-v∥\right)-⟨t_k+v,J{x}_k⟩+{∥x_k∥}^2\hfill \\ =\frac{1}{2}\varphi \left(t_k,x_k\right)+\frac{1}{2}\varphi \left(v,x_k\right)-\frac{1}{4}K\left(∥t_k-v∥\right)\hfill \\ \le l+\sigma -\frac{1}{4}K\left({ϵ}_0\right),\hfill \end{array}$$

(4.9)

for all n ≥ 0. Hence

$$l\le \underset{n\to \infty }{\text{lim}}\varphi \left(\frac{t_k+v}{2},x_n\right)=\underset{n\to \infty }{\text{lim}}\varphi \left(\frac{t_k+v}{2},x_{n+k}\right)\le l+\sigma -\frac{1}{4}K\left({ϵ}_0\right)<l+\sigma -\sigma =l.$$

(4.10)

This is a contradiction. So, {w _n } converges strongly to v ∈ F: = Ω ∩ V I(C, A) ∩T^-1(0) ∩ F(S). Consequently, v ∈ F is the unique element of F such that

$$\underset{n\to \infty }{\text{lim}}\varphi \left(v,x_n\right)=\underset{y\in F}{\text{min}}\underset{n\to \infty }{\text{lim}}\varphi \left(y,x_n\right).$$

(4.11)

This completes the proof. □

Theorem 4.2. Let E be a 2-uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E. Let T: E → E* be a maximal monotone operator satisfying D(T) ⊂ C. Let J _r = (J + rT)^-1 J for r > 0, let A be an α-inverse-strongly monotone operator of C into E* and S be a relatively nonexpansive mappings from C into itself, with $F:=VI\left(C,A\right)\cap T^{-1}\left(0\right)\cap F\left(S\right)\ne \cancel{0}$. Assume that A an operator of C into E* that satisfies the conditions (C1)-(C3). Let {x _n } be a sequence generated by x₁ = x ∈ C and,

$$\left\{\begin{array}{c}{z}_n={\Pi }_C{J}^{-1}\left(J{x}_n-{\lambda }_{n}A{x}_n\right),\hfill \\ y_n=J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{J}_{r_n}{z}_n\right),\hfill \\ x_{n+1}={\Pi }_C{J}^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right),\hfill \end{array}\right.$$

(4.12)

for all n ∈ ℕ, where Π _C is the generalized projection from E onto C, J is the duality mapping on E. The coefficient sequence {a _n } ⊂ [0, 1], {β _n } ⊂ (0, 1], {r _n } ⊂ (0, ∞) satisfying ${\sum }_{n=1}^{\infty }{\alpha }_n<\infty$, lim sup_n→∞β _n < 1, lim inf_n→∞r _n > 0 and {λ _n } ⊂ [a, b] for some a, b with $0<a\le {\lambda }_n\le b<\frac{c^2\alpha }{2}$, $\frac{1}{c}$ is the 2-uniformly convexity constant of E. Then the sequence {Π _F x _n } converges strongly to an element v of F, which is a unique element of F satisfying

$$\underset{n\to \infty }{\text{lim}}\varphi \left(v,x_n\right)=\underset{y\in F}{\text{min}}\underset{n\to \infty }{\text{lim}}\varphi \left(y,x_n\right).$$

Now, we prove a weak convergence theorem for the algorithm (4.13) below under different condition on data.

Theorem 4.3. Let E be a 2-uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E. Let Θ be a bifunction from C × C to ℝ satisfying (A1)-(A4) let φ: C → ℝ be a proper lower semicontinuous and convex function, let T: E → E* be a maximal monotone operator satisfying D(T) ⊂ C. Let J _r = (J + rT)^-1 J for r > 0 and let A be an α-inverse-strongly monotone operator of C into E*, let B: C → E* be a continuous and monotone mappings and S be a relatively nonexpansive mappings from C into itself, with $F:=\Omega \cap VI\left(C,A\right)\cap T^{-1}\left(0\right)\cap F\left(S\right)\ne \cancel{0}$. Assume that A an operator of C into E* that satisfies the conditions (C1)-(C3). Let {x _n } be a sequence generated by x₁ = x ∈ C and,

$$\left\{\begin{array}{c}{u}_n=K_{r_n}{x}_n,\hfill \\ z_n={\Pi }_C{J}^{-1}\left(J{u}_n-{\lambda }_{n}A{u}_n\right),\hfill \\ y_n=J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{J}_{r_n}{z}_n\right),\hfill \\ x_{n+1}={\Pi }_C{J}^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right),\hfill \end{array}\right.$$

(4.13)

for all n ∈ ℕ, where Π _C is the generalized projection from E onto C, J is the duality mapping on E. The coefficient sequence {α _n } ⊂ [0, 1], {βn} ⊂ (0, 1], {r _n } ⊂ (0, ∞) satisfying ${\sum }_{n=1}^{\infty }{\alpha }_n<\infty$, lim sup_n→∞β _n < 1, lim inf_n→∞r _n > 0 and {λ _n } ⊂ [a, b] for some a, b with $0<a\le {\lambda }_n\le b<\frac{c^2\alpha }{2}$, $\frac{1}{c}$ is the 2-uniformly convexity constant of E. Then the sequence {x _n } converges weakly to an element v of F , where v = lim_n→∞Π _F x _n .

Proof . As in Proof of Theorem 3.1, we have {x _n } is bounded, there exists a subsequence $\left\{x_{n_i}\right\}$ of {x _n } such that $x_{n_i}\rightharpoonup u\in C$ and hence u ∈ F: = Ω ∩ V I(C, A)∩T^-1(0)∩F(S). By Theorem 4.1 the {Π _F x _n } converges strongly to a point v ∈ F which is a unique element of F such that

$$\underset{n\to \infty }{\text{lim}}\varphi \left(v,x_n\right)=\underset{y\in F}{\text{min}}\underset{n\to \infty }{\text{lim}}\varphi \left(y,x_n\right).$$

(4.14)

By the uniform smoothness of E, we also have ${\displaystyle {\text{lim}}_{n\to \infty }}∥J{\prod }_F{x}_{n_i}-Jv∥=0$.

Finally, we prove u = v. From Lemma 2.5 and u ∈ F, we have

$$⟨{\Pi }_F{x}_{n_i}-u,J{x}_{n_i}-J{\Pi }_F{x}_{n_i}⟩\ge 0$$

Since J is weakly sequentially continuous, $u_{n_i}\rightharpoonup u$ and u _n - x _n → 0, then

$$⟨v-u,Ju-Jv⟩\ge 0.$$

On the other hand, since J is monotone, we have

$$⟨v-u,Ju-Jv⟩\le 0.$$

Hence,

$$⟨v-u,Ju-Jv⟩=0.$$

Since E is strict convexity, it follows that u = v. Therefore the sequence {x _n } converges weakly to v = lim_n→∞Π _F x _n . This completes the proof. □

Theorem 4.4. Let E be a 2-uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E. Let T: E → E* be a maximal monotone operator satisfying D(T) ⊂ C. Let J _r = (J + rT)^-1 J for r > 0, let A be an α-inverse-strongly monotone operator of C into E* and S be a relatively nonexpansive mappings from C into itself, with $F:=VI\left(C,A\right)\cap T^{-1}\left(0\right)\cap F\left(S\right)\ne \cancel{0}$. Assume that A an operator of C into E* that satisfies the conditions (C1)-(C3). Let {x _n } be a sequence generated by x₁ = x ∈ C and,

$$\left\{\begin{array}{c}{z}_n={\Pi }_C{J}^{-1}\left(J{x}_n-{\lambda }_{n}A{x}_n\right),\hfill \\ y_n=J^{-1}\left({\beta }_{n}J{x}_n+\left(1-{\beta }_n\right)JS{J}_{r_n}{z}_n\right),\hfill \\ x_{n+1}={\Pi }_C{J}^{-1}\left({\alpha }_{n}J{x}_1+\left(1-{\alpha }_n\right)J{y}_n\right),\hfill \end{array}\right.$$

(4.15)

for all n ∈ ℕ, where Π _C is the generalized projection from E onto C, J is the duality mapping on E. The coefficient sequence {α _n } ⊂ [0, 1], {β _n } ⊂ (0, 1], {r _n } ⊂ (0, ∞) satisfying ${\sum }_{n=1}^{\infty }{\alpha }_n<\infty$, lim sup_n→∞β _n < 1, lim inf_n→∞r _n > 0 and {λ _n } ⊂ [a, b] for some a, b with $0<a\le {\lambda }_n\le b<\frac{c^2\alpha }{2}$ , $\frac{1}{c}$ is the 2-uniformly convexity constant of E. Then the sequence {x _n } converges weakly to an element v of F, where v = lim_n→∞Π _F x _n .