Abstract
In this article, we characterize the pairs (u, v) of positive measurable functions such that T maps the weighted amalgam  in (Lp (u), ℓ q ) for all
in (Lp (u), ℓ q ) for all  , where T belongs to a class of positive operators which includes Hardy operators, maximal operators, and fractional integrals.
, where T belongs to a class of positive operators which includes Hardy operators, maximal operators, and fractional integrals.
2000 Mathematics Subject Classification 26D10, 26D15 (42B35)
Similar content being viewed by others
1. Introduction
Let u be a positive function of one real variable and let p, q > 1. The amalgam (Lp (u), ℓ q ) is the space of one variable real functions which are locally in Lp (u) and globally in ℓ q . More precisely,

where

These spaces were introduced by Wiener in [1]. The article [2] describes the role played by amalgams in Harmonic Analysis.
Carton-Lebrun, Heinig, and Hoffmann studied in [3] the boundedness of the Hardy operator  in weighted amalgam spaces. They characterized the pairs of weights (u, v) such that the inequality
in weighted amalgam spaces. They characterized the pairs of weights (u, v) such that the inequality

holds for all f, with a constant C independent of f, whenever 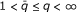 . The characterization of the pairs (u, v) for (1.1) to hold in the case
. The characterization of the pairs (u, v) for (1.1) to hold in the case 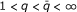 has been recently completed by Ortega and Ramírez ([4]), who have also characterized the weak type inequality
has been recently completed by Ortega and Ramírez ([4]), who have also characterized the weak type inequality

where 
There are several articles dealing with the boundedness in weighted amalgams of other operators different from Hardy's one. Specifically, Carton-Lebrun, Heinig, and Hoffmann studied in [3] weighted inequalities in amalgams for the Hardy-Littlewood maximal operator as well as for some integral operators with kernel K(x, y) increasing in the second variable and decreasing in the first one. On the other hand, Rakotondratsimba ([5]) characterized some weighted inequalities in amalgams (corresponding to the cases 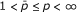 and
and 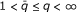 ) for the fractional maximal operators and the fractional integrals. Finally, the authors characterized in [6] the weighted inequalities for some generalized Hardy operators, including the fractional integrals of order greater than one, in all cases
) for the fractional maximal operators and the fractional integrals. Finally, the authors characterized in [6] the weighted inequalities for some generalized Hardy operators, including the fractional integrals of order greater than one, in all cases  , extending also results due to Heinig and Kufner [7].
, extending also results due to Heinig and Kufner [7].
Analyzing the results in the articles cited above, one can see some common features that lead to explore the possibility of giving a general theorem characterizing the boundedness in weighted amalgams of a wide family of positive operators, and providing, in such a way, a unified approach to the subject. This is the purpose of this article.
2. The results
We consider an operator T acting on real measurable functions f of one real variable and define a sequence {T n }n∈ℤof local operators by

We assume that there exists a discrete operator Td, i.e., which transforms sequences of real numbers in sequences of real numbers, verifying the following conditions:
-
(i)
There exists C > 0 such that for all non-negative functions f, all n ∈ ℤ and all x ∈ (n, n + 1), the inequality
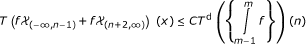 (2.1)
(2.1)
holds.
-
(ii)
There exists C > 0 such that for all sequences {a k } of non-negative real numbers and n ∈ ℤ, the inequality
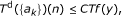 (2.2)
(2.2)
holds for all y ∈ (n, n + 1) and all non-negative f such that  for all m.
for all m.
We also assume that T verifies Tf = T |f|, T(λf) = |λ| Tf, T(f + g)(x) ≤ Tf (x) + Tg (x) and Tf(x) ≤ Tg(x) if 0 ≤ f (x) ≤ g(x).
We will say that an operator T verifying all the above conditions is admissible.
There is a number of important admissible operators in Analysis. For instance: Hardy operators, Hardy-Littlewood maximal operators, Riemann-Liouville, and Weyl fractional integral operators, maximal fractional operators, etc.
Our main result is the following one:
Theorem 1. Let . Let u and v be positive locally integrable functions on ℝ and let T be an admissible operator. Then there exists a constant C > 0 such that the inequality
. Let u and v be positive locally integrable functions on ℝ and let T be an admissible operator. Then there exists a constant C > 0 such that the inequality

holds for all measurable functions f if and only if the following conditions hold:
-
(i)
T d is bounded from
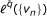 to ℓq({u
n
}), where
to ℓq({u
n
}), where  and
and 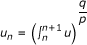 .
. -
(ii)
(a)
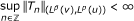 in the case
in the case 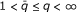 .
.
(b)  , with
, with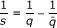 , in the case
, in the case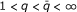 .
.
The proof of Theorem 1 is contained in Sect. 3.
Working as in Theorem 1, we can also prove the following weak type result:
Theorem 2. Let . Let u and v be positive locally integrable functions on ℝ and let T be an admissible operator. Then there exists a constant C > 0 such that the inequality
. Let u and v be positive locally integrable functions on ℝ and let T be an admissible operator. Then there exists a constant C > 0 such that the inequality

holds for all measurable functions f if and only if the following conditions hold:
-
(i)
T d is bounded from
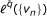 to ℓ q ({u
n
}),), with v
n
and un defined as in Theorem 1.
to ℓ q ({u
n
}),), with v
n
and un defined as in Theorem 1. -
(ii)
(a)
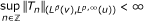 in the case
in the case 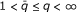 .
.
(b)  , with
, with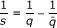 , in the case
, in the case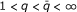 .
.
If conditions on the weights u, v, and {u n }, {v n } characterizing the boundedness of the operators T n and Td, respectively, are available in the literature, we immediately obtain, by applying Theorems 1 and 2, conditions guaranteeing the boundedness of T between the weighted amalgams. In this sense, our result includes, as particular cases, most of the results cited above from the papers [3–7], as well as other corresponding to operators whose behavior on weighted amalgams has not been studied yet.
Thus, if M - is the one-sided Hardy-Littlewood maximal operator defined by

we have:
-
(i)
The discrete operator (M - )d, defined by
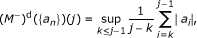
verifies conditions (2.1) and (2.2).
-
(ii)
The local operators
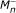 are defined by
are defined by 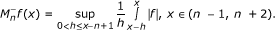
-
(iii)
If
 and
and 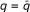 , there are well-known conditions on the weights u, v, and {u
n
}, {v
n
} that characterize the boundedness of
, there are well-known conditions on the weights u, v, and {u
n
}, {v
n
} that characterize the boundedness of 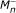 and (M - )d (see, for instance [8–10]).
and (M - )d (see, for instance [8–10]).
Therefore, we obtain the following result:
Theorem 3. The following statements are equivalent:
-
(i)
M - is bounded from (Lp (w), ℓ q ) to (Lp (w), ℓ q ).
-
(ii)
M - is bounded from (L p(w), ℓq) to (L p,∞(w), ℓq).
-
(iii)
The next conditions hold simultaneously:
-
(a)
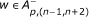 for all n, uniformly, and
for all n, uniformly, and -
(b)
the pair ({u n }, {v n }) verifies the discrete Sawyer's condition
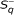 , i.e., there exists C > 0 such that
, i.e., there exists C > 0 such that 
for all r, k ∈ ℤ with r ≤ k.
We can state a similar result for the one-sided maximal operator M+. In this case, the operator (M+)d defined by

verifies conditions (2.1) and (2.2). The theorem is the next one:
Theorem 4. The following statements are equivalent:
-
(i)
M + is bounded from (Lp (w), ℓ q ) to (Lp (w), ℓ q ).
-
(ii)
M + is bounded from (L p(w), ℓq) to (L p,∞(w), ℓq).
-
(iii)
The next conditions hold simultaneously:
-
(a)
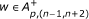 for all n, uniformly, and
for all n, uniformly, and -
(b)
the pair ({u n }, {v n- 3}) verifies the discrete Sawyer's condition
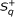 , i.e., there exists C > 0 such that
, i.e., there exists C > 0 such that 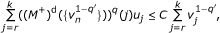
for all r, k ∈ ℤ with r ≤ k.
If M is the Hardy-Littlewood maximal operator, defined by

then M is admissible, with  , and there are well-known results, due to Muckenhoupt ([11]) and Sawyer ([12]), which characterize the boundedness of M in weighted Lebesgue spaces. Applying Theorems 1 and 2, we get the following result:
, and there are well-known results, due to Muckenhoupt ([11]) and Sawyer ([12]), which characterize the boundedness of M in weighted Lebesgue spaces. Applying Theorems 1 and 2, we get the following result:
Theorem 5. The following statements are equivalent:
-
(i)
M is bounded from (Lp (w), ℓ q ) to (Lp (w), ℓ q ).
-
(ii)
M is bounded from (L p(w), ℓq) to (L p,∞(w), ℓq).
-
(iii)
The next conditions hold simultaneously:
-
(a)
w ∈ A p,(n-1,n+2) for all n, uniformly, and
-
(b)
the pair ({u n }, {v n }) verifies the discrete two-sided Sawyer's condition S q , i.e., there exists C > 0 such that
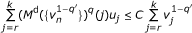
for all r, k ∈ ℤ with r ≤ k.
This result improves the one obtained by Carton-Lebrun, Heinig and Hofmann in [3], in the sense that the conditions we give are necessary and sufficient for the boundedness of the maximal operator in the amalgam (Lp (w), ℓ q ), while in [3] only sufficient conditons were given. We also prove the equivalence between the strong type inequality and the weak type inequality. The equivalence (i) ⇔ (iii) in Theorem 5 is included in Rakotondratsimba's paper [5], where the proof of the admissibility of M can also be found.
Finally, we will apply our results to the fractional maximal operator M α , 0 < α < 1, defined by

The proof of the admissibility of M
α
, with the obvious  , is implied in Rakotondratsimba's paper ([5]).
, is implied in Rakotondratsimba's paper ([5]).
Verbitsky ([13]) in the case 1 < q < p < ∞ and Sawyer ([12]) in the case 1 < p ≤ q < ∞ characterized the boundedness of M
α
from Lp to Lq (w). These results allow us to give necessary and sufficient conditions on the weight u for M
α
to be bounded from  to
to  .
.
Before stating the theorem, we introduce the notation:
-
(i)
If
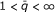 , we define H : ℤ → ℝ by
, we define H : ℤ → ℝ by 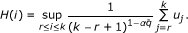
-
(ii)
If
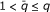 , we define
, we define 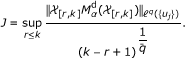
-
(iii)
If
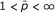 and n ∈ ℤ, we define for x ∈ (n - 1, n + 2)
and n ∈ ℤ, we define for x ∈ (n - 1, n + 2) 
-
(iv)
If
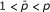 and n ∈ ℤ, we define
and n ∈ ℤ, we define 
The result reads as follows.
Theorem 6. M
α
is bounded from to (Lp (u), ℓ q ) if and only if
to (Lp (u), ℓ q ) if and only if
-
(i)
in the case
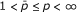 and
and 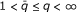 , supn∈ℤ J n < ∞ and J < ∞;
, supn∈ℤ J n < ∞ and J < ∞; -
(ii)
in the case
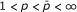 and
and 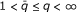 ,
, 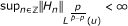 and J < ∞;
and J < ∞; -
(iii)
in the case
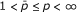 and
and 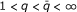 , {J
n
}
n
∈ ℓs, where
, {J
n
}
n
∈ ℓs, where 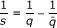 , and
, and 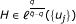 ;
; -
(iv)
in the case
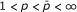 and
and 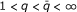 ,
, 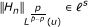 and
and 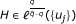 .
.
3. Proof of Theorem 1
Let us suppose that the inequality (2.3) holds. Let n ∈ ℤ and let f be a non-negative function supported in (n - 1, n + 2). Then, on one hand,

and, on the other hand,

Therefore, by (2.3), T
n
is bounded and  , where C is a positive constant independent of n. Then (ii)a holds independently of the relationship between q and
, where C is a positive constant independent of n. Then (ii)a holds independently of the relationship between q and  . Let us prove that if
. Let us prove that if 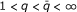 , then (ii)b also holds.
, then (ii)b also holds.
It is well known that  . Therefore, for each n there exists a non-negative measurable function f
n
, with support in (n - 1, n + 2) and with
. Therefore, for each n there exists a non-negative measurable function f
n
, with support in (n - 1, n + 2) and with  , such that
, such that  .
.
Since  , to prove that
, to prove that  it suffices to see that
it suffices to see that  .
.
Let {a
n
} be a sequence of non-negative real numbers and  . For each n ∈ ℤ, f(x) ≥ a
n
f
n
(x) and then Tf (x) ≥ a
n
T
n
f
n
(x) for all x ∈ (n - 1, n + 2). Thus,
. For each n ∈ ℤ, f(x) ≥ a
n
f
n
(x) and then Tf (x) ≥ a
n
T
n
f
n
(x) for all x ∈ (n - 1, n + 2). Thus,

Then, from (2.3) we deduce

This means that the identity operator is bounded from  to
to  . Then
. Then  , by applying the following lemma (see [4]).
, by applying the following lemma (see [4]).
Lemma 1. Let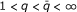 and
and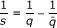 . Suppose that {u
n
} and {v
n
} are sequences of positive real numbers. The following statements are equivalent:
. Suppose that {u
n
} and {v
n
} are sequences of positive real numbers. The following statements are equivalent:
-
(i)
There exists C > 0 such that the inequality
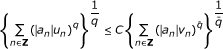
holds for all sequences {a n } of real numbers.
-
(ii)
The sequence
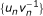 belongs to the space l s.
belongs to the space l s.
On the other hand, let us prove that (i) holds. If {a m } is a a sequence of non-negative real numbers and

then  and by the properties of the operator T we have
and by the properties of the operator T we have

Applying (2.3) we obtain

which means that the discrete operator Td is bounded from 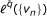 to ℓ q ({u
n
}), as we wished to prove.
to ℓ q ({u
n
}), as we wished to prove.
Conversely, let us suppose that (i) and (ii) hold. Then, we have

where  .
.
Applying that Td is bounded from 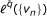 to ℓ q ({u
n
}) and Hölder inequality, we obtain
to ℓ q ({u
n
}) and Hölder inequality, we obtain

Now we estimate I2. If 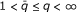 , since (ii)a holds, we know that the operators T
n
are uniformly bounded from Lp(u, (n - 1, n + 2)) to
, since (ii)a holds, we know that the operators T
n
are uniformly bounded from Lp(u, (n - 1, n + 2)) to  and then
and then

Let us suppose, finally, that 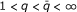 . Then (ii)b holds and, therefore,
. Then (ii)b holds and, therefore,

This finishes the proof of the theorem.
References
Wiener N: On the representation of functions by trigonometric integrals. Math Z 1926, 24: 575–616. 10.1007/BF01216799
Fournier JJF, Stewart J: Amalgams of Lp and ℓ q . Bull Am Math Soc 1985,13(1):1–21. 10.1090/S0273-0979-1985-15350-9
Carton-Lebrun C, Heinig HP, Hofmann SC: Integral operators on weighted amalgams. Stud Math 1994,109(2):133–157.
Ortega Salvador P, Ramírez Torreblanca C: Hardy operators on weighted amalgams. Proc Roy Soc Edinburgh 2010, 140A: 175–188.
Rakotondratsimba Y: Fractional maximal and integral operators on weighted amalgam spaces. J Korean Math Soc 1999,36(5):855–890.
Aguilar Cañestro MI, Ortega Salvador P: Boundedness of generalized Hardy operators on weighted amalgam spaces. Math Inequal Appl 2010,13(2):305–318.
Heinig HP, Kufner A: Weighted Friedrichs inequalities in amalgams. Czechoslovak Math J 1993,43(2):285–308.
Andersen K: Weighted inequalities for maximal functions associated with general measures. Trans Am Math Soc 1991, 326: 907–920. 10.2307/2001788
Martín-Reyes FJ, Ortega Salvador P, de la Torre A: Weighted inequalities for one-sided maximal functions. Trans Am Math Soc 1990,319(2):517–534. 10.2307/2001252
Sawyer ET: Weighted inequalities for the one-sided Hardy-Littlewood maximal functions. Trans Am Math Soc 1986, 297: 53–61. 10.1090/S0002-9947-1986-0849466-0
Muckenhoupt B: Weighted norm inequalities for the Hardy maximal function. Trans Am Math Soc 1972, 165: 207–226.
Sawyer ET: A characterization of a two-weight norm inequality for maximal operators. Stud Math 1982, 75: 1–11.
Verbitsky IE: Weighted norm inequalities for maximal operators and Pisier's Theorem on factorization through Lp, ∞. Integr Equ Oper Theory 1992, 15: 124–153. 10.1007/BF01193770
Acknowledgements
This research has been supported in part by MEC, grant MTM 2008-06621-C02-02, and Junta de Andalucía, Grants FQM354 and P06-FQM-01509.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
Both authors participated similarly in the conception and proofs of the results. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aguilar Cañestro, M.I., Ortega Salvador, P. Boundedness of positive operators on weighted amalgams. J Inequal Appl 2011, 13 (2011). https://doi.org/10.1186/1029-242X-2011-13
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-13




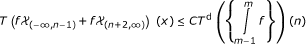
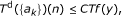
 and
and 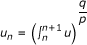 .
.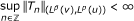 in the case
in the case 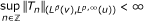 in the case
in the case 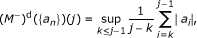
 are defined by
are defined by 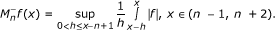
 and
and 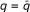 , there are well-known conditions on the weights u, v, and {u
n
}, {v
n
} that characterize the boundedness of
, there are well-known conditions on the weights u, v, and {u
n
}, {v
n
} that characterize the boundedness of 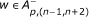 for all n, uniformly, and
for all n, uniformly, and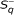 , i.e., there exists C > 0 such that
, i.e., there exists C > 0 such that 
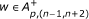 for all n, uniformly, and
for all n, uniformly, and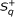 , i.e., there exists C > 0 such that
, i.e., there exists C > 0 such that 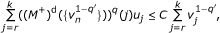
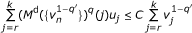
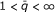 , we define H : ℤ → ℝ by
, we define H : ℤ → ℝ by 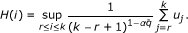
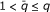 , we define
, we define 
 and n ∈ ℤ, we define for x ∈ (n - 1, n + 2)
and n ∈ ℤ, we define for x ∈ (n - 1, n + 2) 
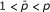 and n ∈ ℤ, we define
and n ∈ ℤ, we define 
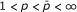 and
and 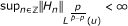 and J < ∞;
and J < ∞;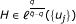 ;
;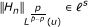 and
and 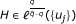 .
.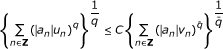
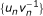 belongs to the space l s.
belongs to the space l s.