Abstract
Matthews (1994) introduced a new distance  on a nonempty set
on a nonempty set  , which is called partial metric. If
, which is called partial metric. If  is a partial metric space, then
is a partial metric space, then  may not be zero for
may not be zero for  . In the present paper, we give some fixed point results on these interesting spaces.
. In the present paper, we give some fixed point results on these interesting spaces.
Similar content being viewed by others
1. Introduction
There are a lot of fixed and common fixed point results in different types of spaces. For example, metric spaces, fuzzy metric spaces, and uniform spaces. One of the most interesting is partial metric space, which is defined by Matthews [1]. In partial metric spaces, the distance of a point in the self may not be zero. After the definition of partial metric space, Matthews proved the partial metric version of Banach fixed point theorem. Then, Valero [2], Oltra and Valero [3], and Altun et al. [4] gave some generalizations of the result of Matthews. Again, Romaguera [5] proved the Caristi type fixed point theorem on this space.
First, we recall some definitions of partial metric spaces and some properties of theirs. See [1–3, 5–7] for details.
A partial metric on a nonempty set  is a function
is a function  such that for all
such that for all 
(p1) ,
,
(p2) ,
,
(p3) ,
,
(p4) .
.
A partial metric space is a pair  such that
such that  is a nonempty set and
is a nonempty set and  is a partial metric on
is a partial metric on  . It is clear that if
. It is clear that if  , then from (p1) and (p2)
, then from (p1) and (p2)  . But if
. But if  ,
,  may not be 0. A basic example of a partial metric space is the pair
may not be 0. A basic example of a partial metric space is the pair  , where
, where  for all
for all  . Other examples of partial metric spaces, which are interesting from a computational point of view, may be found in [1, 8].
. Other examples of partial metric spaces, which are interesting from a computational point of view, may be found in [1, 8].
Each partial metric  on
on  generates a
generates a  topology
topology  on
on  , which has as a base the family open
, which has as a base the family open  -balls
-balls  , where
, where  for all
for all  and
and  .
.
If  is a partial metric on
is a partial metric on  , then the function
, then the function  given by
given by

is a metric on  .
.
Let  be a partial metric space, then we have the following.
be a partial metric space, then we have the following.
(i)A sequence  in a partial metric space
in a partial metric space  converges to a point
converges to a point  if and only if
if and only if  .
.
(ii)A sequence  in a partial metric space
in a partial metric space  is called a Cauchy sequence if there exists (and is finite)
is called a Cauchy sequence if there exists (and is finite)  .
.
-
(iii)
A partial metric space
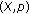 is said to be complete if every Cauchy sequence
is said to be complete if every Cauchy sequence 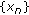 in
in  converges, with respect to
converges, with respect to 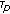 , to a point
, to a point 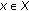 such that
such that 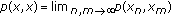 .
. -
(iv)
A mapping
 is said to be continuous at
is said to be continuous at 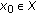 , if for every
, if for every 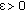 , there exists
, there exists  such that
such that 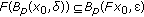 .
.
Let  be a partial metric space.
be a partial metric space.
(a) is a Cauchy sequence in
is a Cauchy sequence in  if and only if it is a Cauchy sequence in the metric space
if and only if it is a Cauchy sequence in the metric space  .
.
(b)A partial metric space  is complete if and only if the metric space
is complete if and only if the metric space  is complete. Furthermore,
is complete. Furthermore,  if and only if
if and only if

On the other hand, existence of fixed points in partially ordered sets has been considered recently in [9], and some generalizations of the result of [9] are given in [10–15] in a partial ordered metric spaces. Also, in [9], some applications to matrix equations are presented; in [14, 15], some applications to ordinary differential equations are given. Also, we can find some results on partial ordered fuzzy metric spaces and partial ordered uniform spaces in [16–18], respectively.
The aim of this paper is to combine the above ideas, that is, to give some fixed point theorems on ordered partial metric spaces.
2. Main Result
Theorem 2.1.
Let  be partially ordered set, and suppose that there is a partial metric
be partially ordered set, and suppose that there is a partial metric  on
on  such that
such that  is a complete partial metric space. Suppose
is a complete partial metric space. Suppose  is a continuous and nondecreasing mapping such that
is a continuous and nondecreasing mapping such that

for all  with
with  , where
, where  is a continuous, nondecreasing function such that
is a continuous, nondecreasing function such that  is convergent for each
is convergent for each  . If there exists an
. If there exists an  with
with  , then there exists
, then there exists  such that
such that  . Moreover,
. Moreover,  .
.
Proof.
From the conditions on  , it is clear that
, it is clear that  for
for  and
and  . If
. If  , then the proof is finished, so suppose
, then the proof is finished, so suppose  . Now, let
. Now, let  for
for  . If
. If  for some
for some  , then it is clear that
, then it is clear that  is a fixed point of
is a fixed point of  . Thus, assume
. Thus, assume  for all
for all  . Notice that since
. Notice that since  and
and  is nondecreasing, we have
is nondecreasing, we have

Now, since  , we can use the inequality (2.1) for these points, then we have
, we can use the inequality (2.1) for these points, then we have

since

and  is nondecreasing. Now, if
is nondecreasing. Now, if

for some  , then from (2.3) we have
, then from (2.3) we have

which is a contradiction since  . Thus
. Thus

for all  . Therefore, we have
. Therefore, we have

and so

On the other hand, since

then from (2.9) we have

Therefore,

This shows that  . Now, we have
. Now, we have

Since  is convergent for each
is convergent for each  , then
, then  is a Cauchy sequence in the metric space
is a Cauchy sequence in the metric space  . Since
. Since  is complete, then, from Lemma 1.1, the sequence
is complete, then, from Lemma 1.1, the sequence  converges in the metric space
converges in the metric space  , say
, say  . Again, from Lemma 1.1, we have
. Again, from Lemma 1.1, we have

Moreover, since  is a Cauchy sequence in the metric space
is a Cauchy sequence in the metric space  , we have
, we have  , and, from (2.11), we have
, and, from (2.11), we have  , thus, from definition
, thus, from definition  , we have
, we have  . Therefore, from (2.14), we have
. Therefore, from (2.14), we have

Now, we claim that  . Suppose
. Suppose  . Since
. Since  is continuous, then, given
is continuous, then, given  , there exists
, there exists  such that
such that  . Since
. Since  , then there exists
, then there exists  such that
such that  for all
for all  . Therefore, we have
. Therefore, we have  for all
for all  . Thus,
. Thus,  , and so
, and so  for all
for all  . This shows that
. This shows that  . Now, we use the inequality (2.1) for
. Now, we use the inequality (2.1) for  , then we have
, then we have

Therefore, we obtain

and letting  , we have
, we have

which is a contradiction since  . Thus,
. Thus,  , and so
, and so  .
.
In the following theorem, we remove the continuity of  . Also, The contractive condition (2.1) does not have to be satisfied for
. Also, The contractive condition (2.1) does not have to be satisfied for  , but we add a condition on
, but we add a condition on  .
.
Theorem 2.2.
Let  be a partially ordered set, and suppose that there is a partial metric
be a partially ordered set, and suppose that there is a partial metric  on
on  such that
such that  is a complete partial metric space. Suppose
is a complete partial metric space. Suppose  is a nondecreasing mapping such that
is a nondecreasing mapping such that

for all  with
with  (i.e.,
(i.e.,  and
and  ), where
), where  is a continuous, nondecreasing function such that
is a continuous, nondecreasing function such that  is convergent for each
is convergent for each  . Also, the condition
. Also, the condition

holds. If there exists an  with
with  , then there exists
, then there exists  such that
such that  . Moreover,
. Moreover,  .
.
Proof.
As in the proof of Theorem 2.1, we can construct a sequence  in
in  by
by  for
for  . Also, we can assume that the consecutive terms of
. Also, we can assume that the consecutive terms of  are different. Otherwise we are finished. Therefore, we have
are different. Otherwise we are finished. Therefore, we have

Again, as in the proof of Theorem 2.1, we can show that  is a Cauchy sequence in the metric space
is a Cauchy sequence in the metric space  , and, therefore, there exists
, and, therefore, there exists  such that
such that

Now, we claim that  . Suppose
. Suppose  . Since the condition (2.20) is satisfied, then we can use (2.19) for
. Since the condition (2.20) is satisfied, then we can use (2.19) for  . Therefore, we obtain
. Therefore, we obtain

using the continuity of  and letting
and letting  , we have
, we have  . Therefore, we obtain
. Therefore, we obtain

which is a contradiction. Thus,  , and so
, and so  .
.
Example 2.3.
Let  and
and  , then it is clear that
, then it is clear that  is a complete partial metric space. We can define a partial order on
is a complete partial metric space. We can define a partial order on  as follows:
as follows:

Let  ,
,

and  ,
,  . Therefore,
. Therefore,  is continuous and nondecreasing. Again we can show by induction that
is continuous and nondecreasing. Again we can show by induction that  , and so we have
, and so we have  that is convergent. Also,
that is convergent. Also,  is nondecreasing with respect to
is nondecreasing with respect to  , and for
, and for  , we have
, we have

that is, the condition (2.19) of Theorem 2.2 is satisfied. Also, it is clear that the condition (2.20) is satisfied, and for  , we have
, we have  . Therefore, all conditions of Theorem 2.2 are satisfied, and so
. Therefore, all conditions of Theorem 2.2 are satisfied, and so  has a fixed point in
has a fixed point in  . Note that if
. Note that if  and
and  , then
, then

This shows that the contractive condition of Theorem 1 of [4] is not satisfied.
Theorem 2.4.
If one uses the following condition instead of (2.1) in Theorem 2.1, one has the same result.

for all  with
with  .
.
In what follows, we give a sufficient condition for the uniqueness of the fixed point in Theorem 2.4, this condition is

In [15], it was proved that condition (2.30) is equivalent to

Theorem 2.5.
Adding condition (2.31) to the hypotheses of Theorem 2.4, one obtains uniqueness of the fixed point of  .
.
Proof.
Suppose that there exists  are different fixed points of
are different fixed points of  , then
, then  . Now, we consider the following two cases.
. Now, we consider the following two cases.
-
(i)
If
 and
and 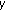 are comparable, then
are comparable, then 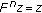 and
and 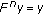 are comparable for
are comparable for 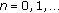 . Therefore, we can use the condition (2.1), then we have
. Therefore, we can use the condition (2.1), then we have 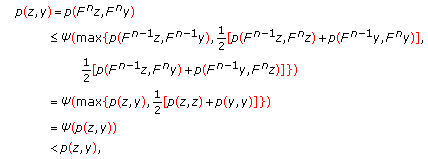 (2.32)
(2.32)
which is a contradiction.
-
(ii)
If
 and
and 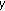 are not comparable, then there exists
are not comparable, then there exists  comparable to
comparable to  and
and  . Since
. Since  is nondecreasing, then
is nondecreasing, then  is comparable to
is comparable to 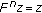 and
and 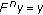 for
for  . Moreover,
. Moreover,  (2.33)
(2.33)
Now, if  for some
for some  , then we have
, then we have

which is a contradiction. Thus,  for all
for all  , and so
, and so

This shows that  is a nonnegative and nondecreasing sequence and so has a limit, say
is a nonnegative and nondecreasing sequence and so has a limit, say  . From the last inequality, we can obtain
. From the last inequality, we can obtain

hence  . Similarly, it can be proven that,
. Similarly, it can be proven that,  . Finally,
. Finally,

and taking limit  , we have
, we have  . This contradicts
. This contradicts  .
.
Consequently,  has no two fixed points.
has no two fixed points.
References
Matthews SG: Partial metric topology. In Proceedings of the 8th Summer Conference on General Topology and Applications, 1994. Volume 728. Annals of the New York Academy of Sciences; 183–197.
Valero O: On Banach fixed point theorems for partial metric spaces. Applied General Topology 2005,6(2):229–240.
Oltra S, Valero O: Banach's fixed point theorem for partial metric spaces. Rendiconti dell'Istituto di Matematica dell'Università di Trieste 2004,36(1–2):17–26.
Altun I, Sola F, Simsek H: Generalized contractions on partial metric spaces. Topology and Its Applications 2010,157(18):2778–2785. 10.1016/j.topol.2010.08.017
Romaguera S: A Kirk type characterization of completeness for partial metric spaces. Fixed Point Theory and Applications 2010, 2010:-6.
Altun I, Simsek H: Some fixed point theorems on dualistic partial metric spaces. Journal of Advanced Mathematical Studies 2008,1(1–2):1–8.
Heckmann R: Approximation of metric spaces by partial metric spaces. Applied Categorical Structures 1999,7(1–2):71–83.
Escardó MH: PCF extended with real numbers. Theoretical Computer Science 1996,162(1):79–115. 10.1016/0304-3975(95)00250-2
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proceedings of the American Mathematical Society 2004,132(5):1435–1443. 10.1090/S0002-9939-03-07220-4
Agarwal RP, El-Gebeily MA, O'Regan D: Generalized contractions in partially ordered metric spaces. Applicable Analysis 2008,87(1):109–116. 10.1080/00036810701556151
Altun I, Simsek H: Some fixed point theorems on ordered metric spaces and application. Fixed Point Theory and Applications 2010, 2010:-17.
Beg I, Butt AR: Fixed point for set-valued mappings satisfying an implicit relation in partially ordered metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(9):3699–3704. 10.1016/j.na.2009.02.027
Ciric L, Cakić N, Rajović M, Ume JS: Monotone generalized nonlinear contractions in partially ordered metric spaces. Fixed Point Theory and Applications 2008, 2008: 11.
Harjani J, Sadarangani K: Generalized contractions in partially ordered metric spaces and applications to ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3–4):1188–1197. 10.1016/j.na.2009.08.003
Nieto JJ, Rodríguez-López R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005,22(3):223–239. 10.1007/s11083-005-9018-5
Altun I: Some fixed point theorems for single and multi valued mappings on ordered non-Archimedean fuzzy metric spaces. Iranian Journal of Fuzzy Systems 2010,7(1):91–96.
Altun I, Miheţ D: Ordered non-Archimedean fuzzy metric spaces and some fixed point results. Fixed Point Theory and Applications 2010, 2010:-11.
Altun I, Imdad M: Some fixed point theorems on ordered uniform spaces. Filomat 2009, 23: 15–22. 10.2298/FIL0903015A
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Altun, I., Erduran, A. Fixed Point Theorems for Monotone Mappings on Partial Metric Spaces. Fixed Point Theory Appl 2011, 508730 (2011). https://doi.org/10.1155/2011/508730
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/508730



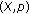 is said to be complete if every Cauchy sequence
is said to be complete if every Cauchy sequence 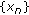 in
in  converges, with respect to
converges, with respect to 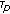 , to a point
, to a point 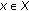 such that
such that 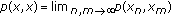 .
. is said to be continuous at
is said to be continuous at 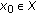 , if for every
, if for every 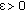 , there exists
, there exists  such that
such that 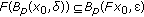 .
. and
and 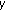 are comparable, then
are comparable, then 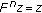 and
and 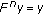 are comparable for
are comparable for 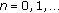 . Therefore, we can use the condition (2.1), then we have
. Therefore, we can use the condition (2.1), then we have 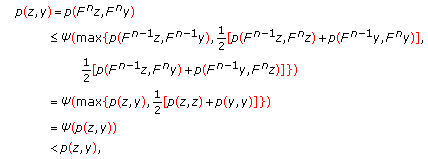
 and
and 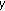 are not comparable, then there exists
are not comparable, then there exists  comparable to
comparable to  and
and  . Since
. Since  is nondecreasing, then
is nondecreasing, then  is comparable to
is comparable to 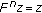 and
and 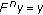 for
for  . Moreover,
. Moreover, 