Abstract
A class of small-deviation theorems for the relative entropy densities of arbitrary random field on the generalized Bethe tree are discussed by comparing the arbitrary measure  with the Markov measure
with the Markov measure  on the generalized Bethe tree. As corollaries, some Shannon-Mcmillan theorems for the arbitrary random field on the generalized Bethe tree, Markov chain field on the generalized Bethe tree are obtained.
on the generalized Bethe tree. As corollaries, some Shannon-Mcmillan theorems for the arbitrary random field on the generalized Bethe tree, Markov chain field on the generalized Bethe tree are obtained.
Similar content being viewed by others
1. Introduction and Lemma
Let  be a tree which is infinite, connected and contains no circuits. Given any two vertices
be a tree which is infinite, connected and contains no circuits. Given any two vertices  , there exists a unique path
, there exists a unique path  from
from  to
to  with
with  distinct. The distance between
distinct. The distance between  and
and  is defined to
is defined to  , the number of edges in the path connecting
, the number of edges in the path connecting  and
and  . To index the vertices on
. To index the vertices on  , we first assign a vertex as the "root" and label it as
, we first assign a vertex as the "root" and label it as  . A vertex is said to be on the
. A vertex is said to be on the  th level if the path linking it to the root has
th level if the path linking it to the root has  edges. The root
edges. The root  is also said to be on the 0th level.
is also said to be on the 0th level.
Definition 1.1.
Let  be a tree with root
be a tree with root  , and let
, and let  be a sequence of positive integers.
be a sequence of positive integers.  is said to be a generalized Bethe tree or a generalized Cayley tree if each vertex on the
is said to be a generalized Bethe tree or a generalized Cayley tree if each vertex on the  th level has
th level has  branches to the
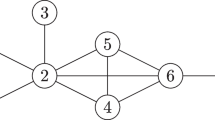
branches to the  th level. For example, when
th level. For example, when  and
and  (
( ),
),  is rooted Bethe tree
is rooted Bethe tree  on which each vertex has
on which each vertex has  neighboring vertices (see Figure 1,
neighboring vertices (see Figure 1,  ), and when
), and when  (
( ),
),  is rooted Cayley tree
is rooted Cayley tree  on which each vertex has
on which each vertex has  branches to the next level.
branches to the next level.
In the following, we always assume that  is a generalized Bethe tree and denote by
is a generalized Bethe tree and denote by  the subgraph of
the subgraph of  containing the vertices from level 0 (the root) to level
containing the vertices from level 0 (the root) to level  . We use
. We use  (
( ) to denote the
) to denote the  th vertex at the
th vertex at the  th level and denote by
th level and denote by  the number of vertices in the subgraph
the number of vertices in the subgraph  . It is easy to see that, for
. It is easy to see that, for  ,
,

Let  ,
,  ,
,  , where
, where  is a function defined on
is a function defined on  and taking values in
and taking values in  , and let
, and let  be the smallest Borel field containing all cylinder sets in
be the smallest Borel field containing all cylinder sets in  . Let
. Let  be the coordinate stochastic process defined on the measurable space
be the coordinate stochastic process defined on the measurable space  ; that is, for any
; that is, for any  , define
, define


Now we give a definition of Markov chain fields on the tree  by using the cylinder distribution directly, which is a natural extension of the classical definition of Markov chains (see [1]).
by using the cylinder distribution directly, which is a natural extension of the classical definition of Markov chains (see [1]).
Definition 1.2.
Let  . One has a strictly positive stochastic matrix on
. One has a strictly positive stochastic matrix on  ,
,  a strictly positive distribution on
a strictly positive distribution on  , and
, and  a measure on
a measure on  . If
. If

Then  will be called a Markov chain field on the tree
will be called a Markov chain field on the tree  determined by the stochastic matrix
determined by the stochastic matrix  and the distribution
and the distribution  .
.
Let  be an arbitrary probability measure defined as (1.3), denote
be an arbitrary probability measure defined as (1.3), denote

 is called the entropy density on subgraph
is called the entropy density on subgraph  with respect to
with respect to  . If
. If  , then by (1.4), (1.5) we have
, then by (1.4), (1.5) we have

The convergence of  in a sense (
in a sense ( convergence, convergence in probability, or almost sure convergence) is called the Shannon-McMillan theorem or the entropy theorem or the asymptotic equipartition property (AEP) in information theory. The Shannon-McMillan theorem on the Markov chain has been studied extensively (see [2, 3]). In the recent years, with the development of the information theory scholars get to study the Shannon-McMillan theorems for the random field on the tree graph (see [4]). The tree models have recently drawn increasing interest from specialists in physics, probability and information theory. Berger and Ye (see [5]) have studied the existence of entropy rate for G-invariant random fields. Recently, Ye and Berger (see [6]) have also studied the ergodic property and Shannon-McMillan theorem for PPG-invariant random fields on trees. But their results only relate to the convergence in probability. Yang et al. [7–9] have recently studied a.s. convergence of Shannon-McMillan theorems, the limit properties and the asymptotic equipartition property for Markov chains indexed by a homogeneous tree and the Cayley tree, respectively. Shi and Yang (see [10]) have investigated some limit properties of random transition probability for second-order Markov chains indexed by a tree.
convergence, convergence in probability, or almost sure convergence) is called the Shannon-McMillan theorem or the entropy theorem or the asymptotic equipartition property (AEP) in information theory. The Shannon-McMillan theorem on the Markov chain has been studied extensively (see [2, 3]). In the recent years, with the development of the information theory scholars get to study the Shannon-McMillan theorems for the random field on the tree graph (see [4]). The tree models have recently drawn increasing interest from specialists in physics, probability and information theory. Berger and Ye (see [5]) have studied the existence of entropy rate for G-invariant random fields. Recently, Ye and Berger (see [6]) have also studied the ergodic property and Shannon-McMillan theorem for PPG-invariant random fields on trees. But their results only relate to the convergence in probability. Yang et al. [7–9] have recently studied a.s. convergence of Shannon-McMillan theorems, the limit properties and the asymptotic equipartition property for Markov chains indexed by a homogeneous tree and the Cayley tree, respectively. Shi and Yang (see [10]) have investigated some limit properties of random transition probability for second-order Markov chains indexed by a tree.
In this paper, we study a class of Shannon-McMillan random approximation theorems for arbitrary random fields on the generalized Bethe tree by comparison between the arbitrary measure and Markov measure on the generalized Bethe tree. As corollaries, a class of Shannon-McMillan theorems for arbitrary random fields and the Markov chains field on the generalized Bethe tree are obtained. Finally, some limit properties for the expectation of the random conditional entropy are discussed.
Lemma 1.3.
Let  and
and  be two probability measures on
be two probability measures on  ,
,  , and let
, and let  be a positive-valued stochastic sequence such that
be a positive-valued stochastic sequence such that

then

In particular, let  , then
, then

Proof (see [11]).
Let

 is called the sample relative entropy rate of
is called the sample relative entropy rate of  relative to
relative to  .
.  is also called the asymptotic logarithmic likelihood ratio. By (1.9)
is also called the asymptotic logarithmic likelihood ratio. By (1.9)

Hence  can be look on as a type of measures of the deviation between the arbitrary random fields and the Markov chain fields on the generalized Bethe tree.
can be look on as a type of measures of the deviation between the arbitrary random fields and the Markov chain fields on the generalized Bethe tree.
2. Main Results
Theorem 2.1.
Let  be an arbitrary random field on the generalized Bethe tree.
be an arbitrary random field on the generalized Bethe tree.  and
and  are, respectively, defined as (1.5) and (1.10). Denote
are, respectively, defined as (1.5) and (1.10). Denote  ,
,  the random conditional entropy of
the random conditional entropy of  relative to
relative to  on the measure
on the measure  , that is,
, that is,

Let


when  ,
,


In particular,

where  is the natural logarithmic,
is the natural logarithmic,  is expectation with respect to the measure
is expectation with respect to the measure  .
.
Proof.
Let  be the probability space we consider,
be the probability space we consider,  an arbitrary constant. Define
an arbitrary constant. Define

denote

We can obtain by (2.7), (2.8) that in the case  ,
,


Therefore,  ,
,  are a class of consistent distributions on
are a class of consistent distributions on  . Let
. Let

then  is a nonnegative supermartingale which converges almost surely (see [12]). By Doob's martingale convergence theorem we have
is a nonnegative supermartingale which converges almost surely (see [12]). By Doob's martingale convergence theorem we have

Hence by (1.3), (1.9), (2.9), and (2.11) we get

By (1.4), (2.8), and (2.11), we have

By (1.10), (2.2), (2.13), and (2.14) we have

By (2.15) we have

By the inequality

 (
( ) and (2.16), (2.17), (2.3), we have in the case of
) and (2.16), (2.17), (2.3), we have in the case of  ,
,

When  , we get by (2.18)
, we get by (2.18)

Let  , in the case
, in the case  , then it is obvious
, then it is obvious  attains, at
attains, at  , its smallest value
, its smallest value  on the interval
on the interval  . We have
. We have

When  , we select
, we select  such that
such that  (
( ). Hence for all
). Hence for all  , it follows from (2.19) that
, it follows from (2.19) that

It is easy to see that (2.20) also holds if  from (2.21).
from (2.21).
Analogously, when  , it follows from (2.18) if
, it follows from (2.18) if  ,
,

Setting  in (2.14), by (2.14) we have
in (2.14), by (2.14) we have

Noticing

By (1.4), (1.5), (2.20), and (2.23), we obtain

Hence (2.4) follows from (2.25). By (1.4), (1.5), (1.10), (2.2), and (2.22), we have

Therefore (2.5) follows from (2.26). Set  in (2.4) and (2.5), (2.6) holds naturally.
in (2.4) and (2.5), (2.6) holds naturally.
Corollary 2.2.
Let  be the Markov chains field determined by the measure
be the Markov chains field determined by the measure  on the generalized Bethe tree
on the generalized Bethe tree  ,
,  are, respectively, defined as (1.6) and (2.3), and
are, respectively, defined as (1.6) and (2.3), and  is defined by (2.1). Then
is defined by (2.1). Then

Proof.
We take  , then
, then  . It implies that (2.2) always holds when
. It implies that (2.2) always holds when  . Therefore
. Therefore  holds. Equation (2.27) follows from (2.3) and (2.6).
holds. Equation (2.27) follows from (2.3) and (2.6).
3. Some Shannon-McMillan Approximation Theorems on the Finite State Space
Corollary 3.1.
Let  be an arbitrary random field which takes values in the alphabet
be an arbitrary random field which takes values in the alphabet  on the generalized Bethe tree.
on the generalized Bethe tree.  ,
,  and
and  are defined as (1.5), (1.10), and (2.2). Denote
are defined as (1.5), (1.10), and (2.2). Denote  ,
,  .
.  is defined as above. Then
is defined as above. Then


Proof.
Set  we consider the function
we consider the function

Then

Let  thus
thus  . Accordingly it can be obtained that
. Accordingly it can be obtained that

By (2.3) and (3.5) we have

Therefore, (2.3) holds naturally. By (2.18) and (3.6) we have

In the case of  , by (3.7) we have
, by (3.7) we have

Let  , in the case
, in the case  , then it is obvious
, then it is obvious  attains, at
attains, at  , its smallest value
, its smallest value  on the interval
on the interval  . That is
. That is

By the similar means of reasoning (2.21), it can be concluded that (3.9) also holds when  . According to the methods of proving (2.4), (3.1) follows from (1.5), (2.23), and (3.9). Similarly, when
. According to the methods of proving (2.4), (3.1) follows from (1.5), (2.23), and (3.9). Similarly, when  ,
,  , by (3.7) we have
, by (3.7) we have

Imitating the proof of (2.5), (3.2) follows from (1.5), (1.10), (2.2), and (3.10).
Corollary 3.2 (see [9]).
Let  be the Markov chains field determined by the measure
be the Markov chains field determined by the measure  on the generalized Bethe tree
on the generalized Bethe tree  is defined as (1.6), and
is defined as (1.6), and  is defined as (2.1). Then
is defined as (2.1). Then

Proof.
By (3.1) and (3.2) in Corollary 3.1, we obtain that when  ,
,

Set  , then
, then  . It implies (2.2) always holds when
. It implies (2.2) always holds when  . Therefore
. Therefore  holds. Equation(3.11) follows from (3.12).
holds. Equation(3.11) follows from (3.12).
Corollary 3.3.
Under the assumption of Corollary 3.1, if  , then
, then

Proof.
It can be obtained that  . holds if
. holds if  (see Gray 1990 [13]), therefore
(see Gray 1990 [13]), therefore  . Equation (3.13) follows from (3.12).
. Equation (3.13) follows from (3.12).
Let  be a Markov chains field on the generalized Bethe tree with the initial distribution and the joint distribution with respect to the measure
be a Markov chains field on the generalized Bethe tree with the initial distribution and the joint distribution with respect to the measure  as follows:
as follows:


where  is a strictly positive stochastic matrix on
is a strictly positive stochastic matrix on  ,
,  is a strictly positive distribution. Therefore, the entropy density of
is a strictly positive distribution. Therefore, the entropy density of  with respect to the measure
with respect to the measure  is
is

Let the initial distribution and joint distribution of  with respect to the measure
with respect to the measure  be defined as (1.4) and (1.5), respectively.
be defined as (1.4) and (1.5), respectively.
We have the following conclusion.
Corollary 3.4.
Let  be a Markov chains field on the generalized Bethe tree
be a Markov chains field on the generalized Bethe tree  whose initial distribution and joint distribution with respect to the measure
whose initial distribution and joint distribution with respect to the measure  and
and  are defined by (3.14), (3.15) and (1.4), (1.5), respectively.
are defined by (3.14), (3.15) and (1.4), (1.5), respectively.  is defined as (3.16). If
is defined as (3.16). If

then


Proof.
Let  in Corollary 3.1, and by (1.5), (3.15) we get (3.16). By the inequalities
in Corollary 3.1, and by (1.5), (3.15) we get (3.16). By the inequalities  ,
,  , (3.17), and (1.10), we obtain
, (3.17), and (1.10), we obtain

By (3.17) and (3.20) we have

It follows from (2.2) and (3.21) that  ; therefore (3.18), (3.19) follow from (3.1), (3.2).
; therefore (3.18), (3.19) follow from (3.1), (3.2).
4. Some Limit Properties for Expectation of Random Conditional Entropy on the Finite State Space
Lemma 4.1 (see [8]).
Let  be a Markov chains field defined on a Bethe tree
be a Markov chains field defined on a Bethe tree  ,
,  be the number of
be the number of  in the set of random variables
in the set of random variables  . then for all
. then for all  ,
,

where  is the stationary distribution determined by
is the stationary distribution determined by  .
.
Theorem 4.2.
Let  be a Markov chains field defined on a Bethe tree
be a Markov chains field defined on a Bethe tree  , and let
, and let  be defined as above. Then
be defined as above. Then

Proof.
Noticing now  , for all
, for all  ,
,  , that therefore we have
, that therefore we have

Noticing that  , by (4.3) we have
, by (4.3) we have

Equation(4.2) follows from (4.4).
Theorem 4.3.
Let  be a Markov chains field defined on a Bethe tree
be a Markov chains field defined on a Bethe tree  ,
,  defined as above. Then
defined as above. Then

Proof.
By the definition of  and properties of conditional expectation, we have
and properties of conditional expectation, we have

Accordingly we have by (4.6)

Therefore (4.5) also holds.
References
Chung KL: A Course in Probability Theory. 2nd edition. Academic Press, New York, NY, USA; 1974:xii+365.
Wen L, Weiguo Y: An extension of Shannon-McMillan theorem and some limit properties for nonhomogeneous Markov chains. Stochastic Processes and their Applications 1996,61(1):129–145. 10.1016/0304-4149(95)00068-2
Liu W, Yang W: Some extensions of Shannon-McMillan theorem. Journal of Combinatorics, Information & System Sciences 1996,21(3–4):211–223.
Ye Z, Berger T: Information Measures for Discrete Random Fields. Science Press, Beijing, China; 1998:iv+160.
Berger T, Ye ZX: Entropic aspects of random fields on trees. IEEE Transactions on Information Theory 1990,36(5):1006–1018. 10.1109/18.57200
Ye Z, Berger T: Ergodicity, regularity and asymptotic equipartition property of random fields on trees. Journal of Combinatorics, Information & System Sciences 1996,21(2):157–184.
Yang W: Some limit properties for Markov chains indexed by a homogeneous tree. Statistics & Probability Letters 2003,65(3):241–250. 10.1016/j.spl.2003.04.001
Yang W, Liu W: Strong law of large numbers and Shannon-McMillan theorem for Markov chain fields on trees. IEEE Transactions on Information Theory 2002,48(1):313–318. 10.1109/18.971762
Yang W, Ye Z: The asymptotic equipartition property for nonhomogeneous Markov chains indexed by a homogeneous tree. IEEE Transactions on Information Theory 2007,53(9):3275–3280.
Shi Z, Yang W: Some limit properties of random transition probability for second-order nonhomogeneous markov chains indexed by a tree. Journal of Inequalities and Applications 2009., 2009:
Liu W, Yang W: Some strong limit theorems for Markov chain fields on trees. Probability in the Engineering and Informational Sciences 2004,18(3):411–422.
Doob JL: Stochastic Processes. John Wiley & Sons, New York, NY, USA; 1953:viii+654.
Gray RM: Entropy and Information Theory. Springer, New York, NY, USA; 1990:xxiv+332.
Acknowledgments
The work is supported by the Project of Higher Schools' Natural Science Basic Research of Jiangsu Province of China (09KJD110002). The author would like to thank the referee for his valuable suggestions. Correspondence author: K. Wang, main research interest is strong limit theory in probability theory. D. Zong main research interest is intelligent algorithm.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, K., Zong, D. Some Shannon-McMillan Approximation Theorems for Markov Chain Field on the Generalized Bethe Tree. J Inequal Appl 2011, 470910 (2011). https://doi.org/10.1155/2011/470910
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/470910





 .
.