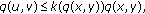Abstract
In the setting of quasimetric spaces, we prove some new results on the existence of fixed points for contractive type maps with respect to  -function. Our results either improve or generalize many known results in the literature.
-function. Our results either improve or generalize many known results in the literature.
Similar content being viewed by others
1. Introduction and Preliminaries
Let  be a metric space with metric
be a metric space with metric  . We use
. We use  to denote the collection of all nonempty subsets of
to denote the collection of all nonempty subsets of  for the collection of all nonempty closed subsets of
for the collection of all nonempty closed subsets of  for the collection of all nonempty closed bounded subsets of
for the collection of all nonempty closed bounded subsets of  and
and  for the Hausdorff metric on
for the Hausdorff metric on  that is,
that is,

where  is the distance from the point
is the distance from the point  to the subset
to the subset 
For a multivalued map  , we say
, we say

 is contraction [1] if there exists a constant
is contraction [1] if there exists a constant  , such that for all
, such that for all  ,
,

 T is weakly contractive [2] if there exist constants
T is weakly contractive [2] if there exist constants  , such that for any
, such that for any  , there is
, there is  satisfying
satisfying

where  .
.
A point  is called a fixed point of a multivalued map
is called a fixed point of a multivalued map  if
if  . We denote
. We denote 
A sequence  in
in  is called an
is called an  of
of  at
at  if
if  for all integer
for all integer  . A real valued function
. A real valued function  on
on  is called lower semicontinuous if for any sequence
is called lower semicontinuous if for any sequence  with
with  implies that
implies that 
Using the Hausdorff metric, Nadler Jr. [1] has established a multivalued version of the well-known Banach contraction principle in the setting of metric spaces as follows.
Theorem 1.1.
Let  be a complete metric space, then each contraction map
be a complete metric space, then each contraction map  has a fixed point.
has a fixed point.
Without using the Hausdorff metric, Feng and Liu [2] generalized Nadler's contraction principle as follows.
Theorem 1.2.
Let  be a complete metric space and let
be a complete metric space and let  be a weakly contractive map, then
be a weakly contractive map, then  has a fixed point in
has a fixed point in  provided the real valued function
provided the real valued function  on
on  is a lower semicontinuous.
is a lower semicontinuous.
In [3], Kada et al. introduced the concept of  -distance in the setting of metric spaces as follows.
-distance in the setting of metric spaces as follows.
A function  is called a
is called a  -distance on
-distance on  if it satisfies the following:
if it satisfies the following:
(w1) for all
for all 
(w2) is lower semicontinuous in its second variable;
is lower semicontinuous in its second variable;
(w3)for any  there exists
there exists  , such that
, such that  and
and  imply
imply 
Note that in general for  ,
,  and not either of the implications
and not either of the implications  necessarily holds. Clearly, the metric
necessarily holds. Clearly, the metric  is a
is a  -distance on
-distance on  . Many other examples and properties of
. Many other examples and properties of  -distances are given in [3].
-distances are given in [3].
In [4], Suzuki and Takahashi improved Nadler contraction principle (Theorem 1.1) as follows.
Theorem 1.3.
Let  be a complete metric space and let
be a complete metric space and let  . If there exist a
. If there exist a  -distance
-distance  on
on  and a constant
and a constant  , such that for each
, such that for each  and
and  , there is
, there is  satisfying
satisfying

then  has a fixed point.
has a fixed point.
Recently, Latif and Albar [5] generalized Theorem 1.2 with respect to  -distance (see, Theorem
-distance (see, Theorem  in [5]), and Latif [6] proved a fixed point result with respect to
in [5]), and Latif [6] proved a fixed point result with respect to  -distance ( see, Theorem
-distance ( see, Theorem  in [6]) which contains Theorem 1.3 as a special case.
in [6]) which contains Theorem 1.3 as a special case.
A nonempty set  together with a quasimetric
together with a quasimetric  (i.e., not necessarily symmetric) is called a quasimetric space. In the setting of a quasimetric spaces, Al-Homidan et al. [7] introduced the concept of a
(i.e., not necessarily symmetric) is called a quasimetric space. In the setting of a quasimetric spaces, Al-Homidan et al. [7] introduced the concept of a  -function on quasimetric spaces which generalizes the notion of a
-function on quasimetric spaces which generalizes the notion of a  -distance.
-distance.
A function  is called a
is called a  -function on
-function on  if it satisfies the following conditions:
if it satisfies the following conditions:
(Q1) for all
for all 
(Q2)If  is a sequence in
is a sequence in  such that
such that  and for
and for  ,
,  for some
for some  , then
, then 
(Q3)for any  there exists
there exists  , such that
, such that  and
and  imply
imply 
Note that every  -distance is a
-distance is a  -function, but the converse is not true in general [7]. Now, we state some useful properties of
-function, but the converse is not true in general [7]. Now, we state some useful properties of  -function as given in [7].
-function as given in [7].
Lemma 1.4.
Let  be a complete quasimetric space and let
be a complete quasimetric space and let  be a
be a  -function on
-function on  . Let
. Let  and
and  be sequences in
be sequences in  . Let
. Let  and
and  be sequences in
be sequences in  converging to
converging to  , then the following hold for any
, then the following hold for any  :
:
(i)if  and
and  for all
for all  then
then  in particular, if
in particular, if  and
and  , then
, then 
(ii)if  and
and  for all
for all  then
then  converges to
converges to  ;
;
(iii)if  for any
for any  with
with  then
then  is a Cauchy sequence;
is a Cauchy sequence;
(iv)if  for any
for any  then
then  is a Cauchy sequence.
is a Cauchy sequence.
Using the concept  -function, Al-Homidan et al. [7] recently studied an equilibrium version of the Ekeland-type variational principle. They also generalized Nadler's fixed point theorem (Theorem 1.1) in the setting of quasimetric spaces as follows.
-function, Al-Homidan et al. [7] recently studied an equilibrium version of the Ekeland-type variational principle. They also generalized Nadler's fixed point theorem (Theorem 1.1) in the setting of quasimetric spaces as follows.
Theorem 1.5.
Let  be a complete quasimetric space and let
be a complete quasimetric space and let  . If there exist
. If there exist  -function
-function  on
on  and a constant
and a constant  , such that for each
, such that for each  and
and  , there is
, there is  satisfying
satisfying

then  has a fixed point.
has a fixed point.
In the sequel, we consider  as a quasimetric space with quasimetric
as a quasimetric space with quasimetric  .
.
Considering a multivalued map  , we say
, we say
-
(c)
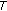 is weakly
is weakly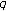 -contractive if there exist
-contractive if there exist 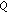 - function
- function  on
on and constants
and constants  ,
, 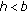 , such that for any
, such that for any 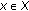 , there is
, there is 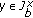 satisfying
satisfying 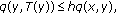 (1.6)
(1.6)
where  and
and 
-
(d)
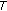 is generalized
is generalized -contractive if there exists a
-contractive if there exists a 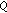 - function
- function 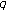 on
on 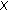 , such that for each
, such that for each 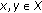 and
and 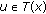 , there is
, there is  satisfying
satisfying 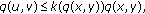 (1.7)
(1.7)
where  is a function of
is a function of  to
to  , such that
, such that  for all
for all 
Clearly, t he class of weakly - contractive maps contains the class of weakly contractive maps, and the class of generalized
- contractive maps contains the class of weakly contractive maps, and the class of generalized  -contractive maps contains the classes of generalized
-contractive maps contains the classes of generalized  -contraction maps [6],
-contraction maps [6],  -contractive maps [4], and
-contractive maps [4], and  -contractive maps [7].
-contractive maps [7].
In this paper, we prove some new fixed point results in the setting of quasimetric spaces for weakly  -contractive and generalized
-contractive and generalized  -contractive multivalued maps. Consequently, our results either improve or generalize many known results including the above stated fixed point results.
-contractive multivalued maps. Consequently, our results either improve or generalize many known results including the above stated fixed point results.
2. The Results
First, we prove a fixed point theorem for weakly  -contractive maps in the setting of quasimetric spaces.
-contractive maps in the setting of quasimetric spaces.
Theorem 2.1.
Let  be a complete quasimetric space and let
be a complete quasimetric space and let  be a weakly
be a weakly  - contractive map. If a real valued function
- contractive map. If a real valued function  on
on  is lower semicontinuous, then there exists
is lower semicontinuous, then there exists  , such that
, such that  Further, if
Further, if  then
then  is
is  a
a  fixed
fixed  point of
point of  .
.
Proof.
Let  Since
Since  is weakly contractive, there is
is weakly contractive, there is  , such that
, such that

where  Continuing this process, we can get an orbit
Continuing this process, we can get an orbit  of
of  at
at  satisfying
satisfying  and
and

Since  and
and  thus we get
thus we get

If we put  , then also we have
, then also we have

Thus, we obtain

and since  , hence the sequence
, hence the sequence  which is decreasing, converges to 0. Now, we show that
which is decreasing, converges to 0. Now, we show that  is a Cauchy sequence. Note that
is a Cauchy sequence. Note that

Now, for any integer  with
with  , we have
, we have

and thus by Lemma 1.4,  is a Cauchy sequence. Due to the completeness of
is a Cauchy sequence. Due to the completeness of  , there exists some
, there exists some  , such that
, such that  Now, since
Now, since  is lower semicontinuous, we have
is lower semicontinuous, we have

and thus,  It follows that there exists a sequence
It follows that there exists a sequence  in
in  , such that
, such that  Now, if
Now, if  then by Lemma 1.4,
then by Lemma 1.4,  . Since
. Since  is closed,
is closed, we
we get
get 
Now, we prove the following useful lemma.
Lemma 2.2.
Let  be a complete quasimetric space and let
be a complete quasimetric space and let  be a generalized
be a generalized  -contractive map, then there exists an orbit
-contractive map, then there exists an orbit  of
of  at
at  , such that the sequence of nonnegative numbers
, such that the sequence of nonnegative numbers  is decreasing to zero and
is decreasing to zero and  is a Cauchy
is a Cauchy  sequence.
sequence.
Proof.
Let  be an arbitrary but fixed element of
be an arbitrary but fixed element of  and let
and let  . Since
. Since  is generalized as a
is generalized as a  -contractive, there is
-contractive, there is  , such that
, such that

Continuing this process, we get a sequence  in
in  , such that
, such that  and
and

Thus, for all  , we have
, we have

Write  . Suppose that
. Suppose that  , then we have
, then we have

Now, taking limits as  on both sides, we get
on both sides, we get

which is not possible, and hence the sequence of nonnegative numbers  which is decreasing, converges to 0. Finally, we show that
which is decreasing, converges to 0. Finally, we show that  is a Cauchy sequence. Let
is a Cauchy sequence. Let  . There exists real number
. There exists real number  such that
such that  . Then for sufficiently large
. Then for sufficiently large  ,
,  , and thus for sufficiently large
, and thus for sufficiently large  , we have
, we have  Consequently, we obtain
Consequently, we obtain  , that is,
, that is,

Now, for any integers  ,
,

and thus by Lemma 1.4,  is a Cauchy sequence.
is a Cauchy sequence.
Applying Lemma 2.2, we prove a fixed point result for generalized  -contractive maps.
-contractive maps.
Theorem 2.3.
Let  be a complete quasimetric space then each generalized q -contractive map
be a complete quasimetric space then each generalized q -contractive map  has a fixed point.
has a fixed point.
Proof.
It follows from Lemma 2.2 that there exists a Cauchy sequence  in
in  such that the decreasing sequence
such that the decreasing sequence  converges to 0. Due to the completeness of
converges to 0. Due to the completeness of  , there exists some
, there exists some  such that
such that  Let
Let  be arbitrary fixed positive integer then for all positive integers
be arbitrary fixed positive integer then for all positive integers  with
with  , we have
, we have

Let  , then
, then  . Now, note that
. Now, note that

Since  was arbitrary fixed, we have
was arbitrary fixed, we have

Note that  converges to
converges to  . Now, since
. Now, since  and
and  is a generalized
is a generalized  -contractive map, then there is
-contractive map, then there is  , such that
, such that

And for large  , we obtain
, we obtain

thus, we get

Thus, it follows from Lemma 1.4 that  . Since
. Since  is closed, we get
is closed, we get 
Corollary 2.4.
Let  be a complete quasimetric space and
be a complete quasimetric space and  a
a  -function on
-function on  . Let
. Let  be a multivalued map, such that for any
be a multivalued map, such that for any  and
and  , there is
, there is  with
with

where  is a monotonic increasing function from
is a monotonic increasing function from  to
to  , then
, then  has a fixed point.
has a fixed point.
Finally, we conclude with the following remarks concerning our results related to the known fixed point results.
Remark 2.5.
(1)Theorem 2.1 generalizes Theorem 1.2 according to Feng and Liu [2] and Latif and Albar [5, Theorem  ].
].
(2)Theorem 2.3 generalizes Theorem 1.3 according to Suzuki and Takahashi [4] and Theorem 1.5 according to Al-Homidan et al. [7] and contains Latif's Theorem  in [6].
in [6].
(3)Theorem 2.3 also generalizes Theorem  in [8] in several ways.
in [8] in several ways.
(4)Corollary 2.4 improves and generalizes Theorem  in [9].
in [9].
References
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Feng Y, Liu S: Fixed point theorems for multi-valued contractive mappings and multi-valued Caristi type mappings. Journal of Mathematical Analysis and Applications 2006,317(1):103–112. 10.1016/j.jmaa.2005.12.004
Kada O, Suzuki T, Takahashi W: Nonconvex minimization theorems and fixed point theorems in complete metric spaces. Mathematica Japonica 1996,44(2):381–391.
Suzuki T, Takahashi W: Fixed point theorems and characterizations of metric completeness. Topological Methods in Nonlinear Analysis 1997,8(2):371–382.
Latif A, Albar WA: Fixed point results in complete metric spaces. Demonstratio Mathematica 2008,41(1):145–150.
Latif A: A fixed point result in complete metric spaces. JP Journal of Fixed Point Theory and Applications 2007,2(2):169–175.
Al-Homidan S, Ansari QH, Yao J-C: Some generalizations of Ekeland-type variational principle with applications to equilibrium problems and fixed point theory. Nonlinear Analysis: Theory, Methods & Applications 2008,69(1):126–139. 10.1016/j.na.2007.05.004
Siddiqi AH, Ansari QH: An iterative method for generalized variational inequalities. Mathematica Japonica 1989,34(3):475–481.
Kaneko H: Generalized contractive multivalued mappings and their fixed points. Mathematica Japonica 1988,33(1):57–64.
Acknowledgments
The authors thank the referees for their kind comments. The authors also thank King Abdulaziz University and the Deanship of Scientific Research for the research Grant no. 3-35/429.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Latif, A., Al-Mezel, S.A. Fixed Point Results in Quasimetric Spaces. Fixed Point Theory Appl 2011, 178306 (2011). https://doi.org/10.1155/2011/178306
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/178306



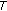 is weakly
is weakly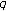 -contractive if there exist
-contractive if there exist 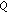 - function
- function  on
on and constants
and constants  ,
, 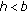 , such that for any
, such that for any 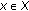 , there is
, there is 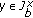 satisfying
satisfying 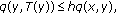
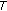 is generalized
is generalized -contractive if there exists a
-contractive if there exists a 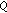 - function
- function 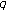 on
on 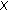 , such that for each
, such that for each 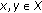 and
and 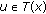 , there is
, there is  satisfying
satisfying