Abstract
We investigate some new nonlinear integral inequalities in two independent variables. The inequalities given here can be used as tools in the qualitative theory of certain nonlinear partial differential equations.
Similar content being viewed by others
1. Introduction
It is well known that the integral inequalities involving functions of one and more than one independent variables which provide explicit bounds on unknown functions play a fundamental role in the development of the theory of differential equations. In the past few years, a number of integral inequalities had been established by many scholars, which are motivated by certain applications. For details, we refer to literatures [1–10] and the references therein. In this paper we investigate some new nonlinear integral inequalities in two independent variables, which can be used as tools in the qualitative theory of certain partial differential equations.
2. Main Results
In what follows,  denotes the set of real numbers and
denotes the set of real numbers and  is the given subset of
is the given subset of  . The first-order partial derivatives of a
. The first-order partial derivatives of a  defined for
defined for  with respect to
with respect to  and
and  are denoted by
are denoted by  , and
, and  respectively. Throughout this paper, all the functions which appear in the inequalities are assumed to be real-valued and all the integrals involved exist on the respective domains of their definitions,
respectively. Throughout this paper, all the functions which appear in the inequalities are assumed to be real-valued and all the integrals involved exist on the respective domains of their definitions,  denotes the class of all continuous functions defined on set
denotes the class of all continuous functions defined on set  with range in the set
with range in the set  ,
,  and
and  are constants, and
are constants, and 
 .
.
We firstly introduce two lemmas, which are useful in our main results.
Lemma 2.1 (Bernoulli's inequality [11]).
Let  and
and  . Then
. Then 
Lemma 2.2 (see [7]).
Let  be nonnegative and continuous functions defined for
be nonnegative and continuous functions defined for 
-
(i)
Assume that
 is nondecreasing for
is nondecreasing for  . If
. If (2.1)
(2.1)for
 , then
, then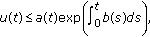 (2.2)
(2.2)for
 .
. -
(ii)
Assume that
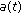 is nonincreasing for
is nonincreasing for  . If
. If (2.3)
(2.3)for
 , then
, then (2.4)
(2.4)for
 .
.Next, we establish our main results.
Theorem 2.3.
Let  and
and  .
.
-
(i)
If
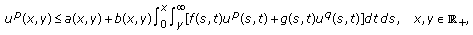 (E1)
(E1)then
 (2.5)
(2.5)where
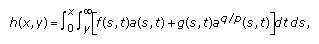 (2.6)
(2.6) (2.7)
(2.7) -
(ii)
If
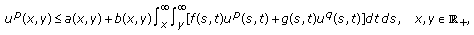 (Ex20321)
(Ex20321)then
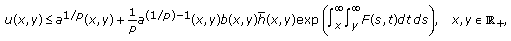 (2.5x2032)
(2.5x2032)where
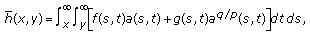 (2.6x2032)
(2.6x2032)and
 is defined by (2.7).
is defined by (2.7).
Proof.
We only give the proof of (i). The proof of (ii) can be completed by following the proof of (i).
-
(i)
Define a function
 by
by 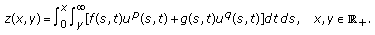 (2.8)
(2.8)
Then can be restated as

Using Lemma 2.1, from (2.9), we easily obtain


Combining (2.8), (2.9), and (2.11), we have

where  and
and  are defined by (2.6) and (2.7), respectively. Obviously,
are defined by (2.6) and (2.7), respectively. Obviously,  is nonnegative, continuous, nondecreasing in
is nonnegative, continuous, nondecreasing in  , and nonincreasing in
, and nonincreasing in  for
for  .
.
Firstly, we assume that  for
for  . From (2.12), we easily observe that
. From (2.12), we easily observe that

Letting

we easily see that  is nonincreasing in
is nonincreasing in  , and
, and

Therefore,

Treating  ,
,  , fixed in (2.16), dividing both sides of (2.16) by
, fixed in (2.16), dividing both sides of (2.16) by  , setting
, setting  , and integrating the resulting inequality from 0 to
, and integrating the resulting inequality from 0 to  , we have
, we have

It follows from (2.15) and (2.17) that

Therefore, the desired inequality (2.5) follows from (2.10) and (2.18).
If  is nonnegative, we carry out the above procedure with
is nonnegative, we carry out the above procedure with  instead of
instead of  , where
, where  is an arbitrary small constant, and subsequently pass to the limit as
is an arbitrary small constant, and subsequently pass to the limit as  to obtain (2.5). This completes the proof.
to obtain (2.5). This completes the proof.
Theorem 2.4.
Assume that  , and
, and  . Let
. Let  , and
, and

for  , where
, where  .
.
-
(i)
If
 (E2)
(E2)then
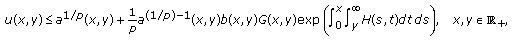 (2.20)
(2.20)where
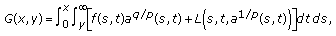 (2.21)
(2.21)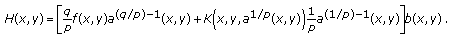 (2.22)
(2.22) -
(ii)
If
 (Ex20322)
(Ex20322)then
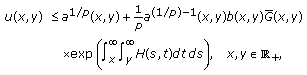 (2.20x2032)
(2.20x2032)where
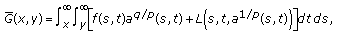 (2.21x2032)
(2.21x2032)and
 is defined by (2.22).
is defined by (2.22).
Proof.
We only prove the part (i). The proof of (ii) can be completed by following the proof of (i).
-
(i)
Define a function
 by
by  (2.23)
(2.23)
Then, as in the proof of Theorem 2.3, we obtain (2.9)–(2.11). Therefore, we have


It follows from (2.23)–(2.25) that

where  and
and  are defined by (2.21) and (2.22), respectively.
are defined by (2.21) and (2.22), respectively.
It is obvious that  is nonnegative, continuous, nondecreasing in
is nonnegative, continuous, nondecreasing in  , and nonincreasing in
, and nonincreasing in  for
for  . By following the proof of Theorem 2.3, from (2.26), we have
. By following the proof of Theorem 2.3, from (2.26), we have

Combining (2.10) and (2.27), we obtain the desired inequality (2.20). The proof is complete.
Theorem 2.5.
Let  , and
, and  be the same as in Theorem 2.4, and
be the same as in Theorem 2.4, and  .
.
-
(i)
Assume that
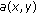 is nondecreasing in
is nondecreasing in 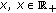 , and the condition (2.19) holds. If
, and the condition (2.19) holds. If (E3)
(E3)then
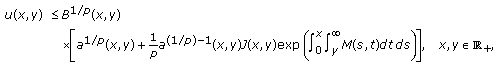 (2.28)
(2.28)where
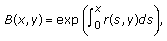 (2.29)
(2.29)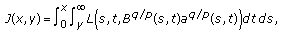 (2.30)
(2.30) (2.31)
(2.31) -
(ii)
Assume that
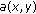 is nonincreasing in
is nonincreasing in  , and the condition (2.19) holds. If
, and the condition (2.19) holds. If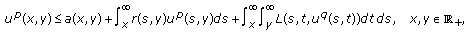 (Ex20323)
(Ex20323)then
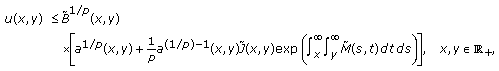 (2.28x2032)
(2.28x2032)where
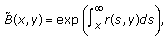 (2.29x2032)
(2.29x2032)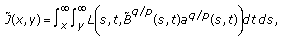 (2.30x2032)
(2.30x2032)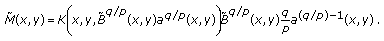 (2.31x2032)
(2.31x2032)
Proof. (i) Define a function by
by

where

Then can be restated as

Noting the assumption that  is nondecreasing in
is nondecreasing in  , we easily see that
, we easily see that  is a nonnegative and nondecreasing function in
is a nonnegative and nondecreasing function in 
 Therefore, treating
Therefore, treating  , fixed in (2.34) and using part (i) of Lemma 2.2 to (2.34), we get
, fixed in (2.34) and using part (i) of Lemma 2.2 to (2.34), we get

that is,

where  is defined by (2.29). Using Lemma 2.1, from (2.36) we have
is defined by (2.29). Using Lemma 2.1, from (2.36) we have


Combining (2.33) and (2.38), and noting the hypotheses (2.19), we obtain

where  and
and  are defined by (2.30) and (2.31), respectively.
are defined by (2.30) and (2.31), respectively.
It is obvious that  is nonnegative, continuous, nondecreasing in
is nonnegative, continuous, nondecreasing in  and nonincreasing in
and nonincreasing in  for
for  . By following the proof of Theorem 2.3, from (2.39), we obtain
. By following the proof of Theorem 2.3, from (2.39), we obtain

Obviously, the desired inequality (2.28) follows from (2.37) and (2.40).
-
(ii)
Noting the assumption that
 is nonincreasing in
is nonincreasing in  and using the part (ii) of Lemma 2.2, we can complete the proof by following the proof of (i) with suitable changes. Therefore, the details are omitted here.
and using the part (ii) of Lemma 2.2, we can complete the proof by following the proof of (i) with suitable changes. Therefore, the details are omitted here.
By using the ideas of the proofs of Theorems 2.5 and 2.3, we easily prove the following theorem.
Theorem 2.6.
Let  , and
, and  .
.
-
(i)
Assume that
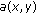 is nondecreasing in
is nondecreasing in 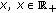 . If
. If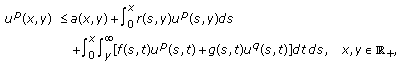 (E4)
(E4)then
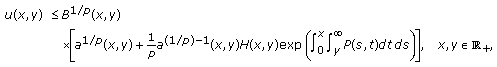 (2.41)
(2.41)where
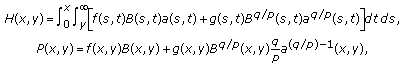 (2.42)
(2.42)and
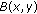 is defined by (2.29).
is defined by (2.29). -
(ii)
Assume that
 is nonincreasing in
is nonincreasing in 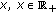 . If
. If (Ex20324)
(Ex20324)then
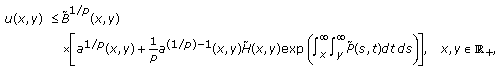 (2.40x2032)
(2.40x2032)where
 (2.41x2032)
(2.41x2032)and
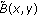 is defined by (25').
is defined by (25').
Remark 2.7.
Noting that  and
and  are constants, and
are constants, and 
 , we can obtain many special integral inequalities by using our main results. For example, let
, we can obtain many special integral inequalities by using our main results. For example, let  , and
, and  , respectively; from Theorem 2.3, we obtain the following corollaries.
, respectively; from Theorem 2.3, we obtain the following corollaries.
Corollary 2.8.
Let  and
and  .
.
-
(i)
If
 (E5)
(E5)then
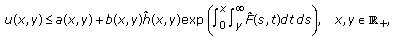 (2.43)
(2.43)where
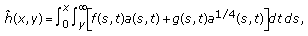 (2.44)
(2.44)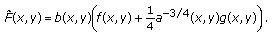 (2.45)
(2.45) -
(ii)
If
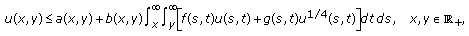 (Ex20325)
(Ex20325)then
 (2.42x2032)
(2.42x2032)where
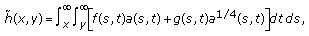 (2.43x2032)
(2.43x2032)and
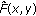 is defined by (2.45).
is defined by (2.45).
Corollary 2.9.
Let  and
and  .
.
-
(i)
If
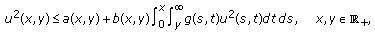 (E6)
(E6)then
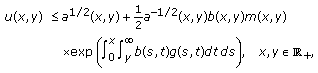 (2.46)
(2.46)where
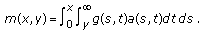 (2.47)
(2.47) -
(ii)
If
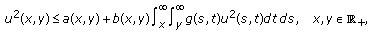 (Ex20326)
(Ex20326)then
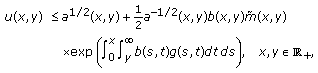 (2.45x2032)
(2.45x2032)where
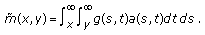 (2.46x2032)
(2.46x2032)
Remark 2.10.
If we add  to the assumptions of [7, Theorems 2.2–2.4], then we easily see that [7, Theorems 2.2–2.4] are special cases of Theorems 2.3, 2.5, and 2.6, respectively. Therefore, our paper gives some extensions of the results of [7] in a sense.
to the assumptions of [7, Theorems 2.2–2.4], then we easily see that [7, Theorems 2.2–2.4] are special cases of Theorems 2.3, 2.5, and 2.6, respectively. Therefore, our paper gives some extensions of the results of [7] in a sense.
3. An Application
In this section, using Theorem 2.3, we obtain the bound on the solution of a nonlinear differential equation.
Example 3.1.
Consider the partial differential equation:

where 

 , and
, and  is a real constant, and
is a real constant, and  is a constant.
is a constant.
Suppose that

where  and
and  for
for  , and
, and  is a constant. Let
is a constant. Let  be a solution of (3.1) for
be a solution of (3.1) for  ; then
; then

where

In fact, if  is a solution of (3.1), then it can be written as (see [1, page 80])
is a solution of (3.1), then it can be written as (see [1, page 80])

for  .
.
It follows from (3.2) and (3.5) that

Now, a suitable application of part (ii) of Theorem 2.3 to (3.6) yields the required estimate in (3.3).
References
Baĭnov D, Simeonov P: Integral Inequalities and Applications, Mathematics and Its Applications (East European Series). Volume 57. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xii+245.
Hacia L: On some integral inequalities and their applications. Journal of Mathematical Analysis and Applications 1997,206(2):611-622. 10.1006/jmaa.1997.5258
Li WN, Sheng W: On some nonlinear integral inequalities with an advanced argument. Communications in Mathematical Analysis 2006,1(1):12-20.
Ma Q-H, Yang E-H: Some new Gronwall-Bellman-Bihari type integral inequalities with delay. Periodica Mathematica Hungarica 2002,44(2):225-238. 10.1023/A:1019600715281
Máté A, Nevai P:Sublinear perturbations of the differential equation
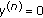 and of the analogous difference equation. Journal of Differential Equations 1984,53(2):234-257. 10.1016/0022-0396(84)90041-X
and of the analogous difference equation. Journal of Differential Equations 1984,53(2):234-257. 10.1016/0022-0396(84)90041-XMeng FW, Li WN: On some new integral inequalities and their applications. Applied Mathematics and Computation 2004,148(2):381-392. 10.1016/S0096-3003(02)00855-X
Pachpatte BG: On some fundamental integral inequalities and their discrete analogues. Journal of Inequalities in Pure and Applied Mathematics 2001., 2, Article 15: http://jipam.vu.edu.au/
Pachpatte BG: Inequalities for Differential and Integral Equations, Mathematics in Science and Engineering. Volume 197. Academic Press, San Diego, Calif, USA; 1998:x+611.
Pachpatte BG: Explicit bounds on certain integral inequalities. Journal of Mathematical Analysis and Applications 2002,267(1):48-61. 10.1006/jmaa.2001.7743
Pachpatte BG: Integral and Finite Difference Inequalities and Applications, North-Holland Mathematics Studies. Volume 205. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:x+309.
Mitrinović DS: Analytic Inequalities. Springer, New York, NY, USA; 1970:xii+400.
Acknowledgment
This work is supported by the National Natural Science Foundation of China (10971018), the Natural Science Foundation of Shandong Province (ZR2009AM005), China Postdoctoral Science Foundation Funded Project (20080440633), Shanghai Postdoctoral Scientific Program (09R21415200), the Project of Science and Technology of the Education Department of Shandong Province (J08LI52), and the Doctoral Foundation of Binzhou University (2006Y01).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, W. Some Nonlinear Integral Inequalities in Two Independent Variables. Adv Differ Equ 2010, 984141 (2010). https://doi.org/10.1155/2010/984141
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/984141



 is nondecreasing for
is nondecreasing for  . If
. If
 , then
, then
 .
.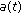 is nonincreasing for
is nonincreasing for  . If
. If
 , then
, then
 .
.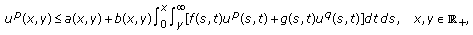

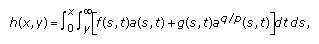

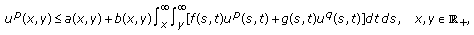
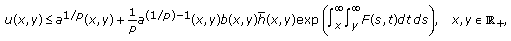
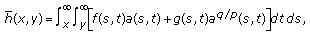
 is defined by (2.7).
is defined by (2.7). by
by 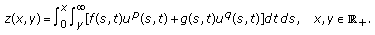

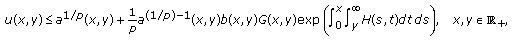
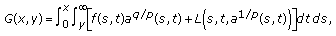
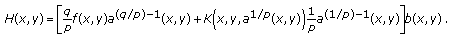

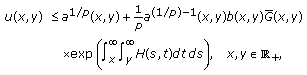
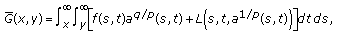
 is defined by (2.22).
is defined by (2.22). by
by 
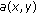 is nondecreasing in
is nondecreasing in 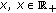 , and the condition (2.19) holds. If
, and the condition (2.19) holds. If
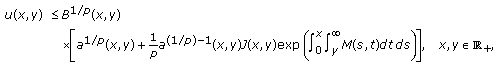
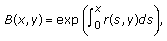
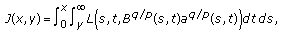

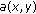 is nonincreasing in
is nonincreasing in  , and the condition (2.19) holds. If
, and the condition (2.19) holds. If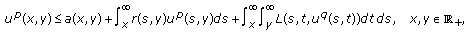
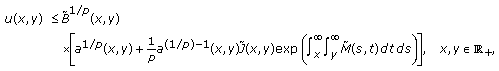
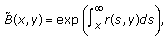
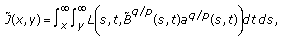
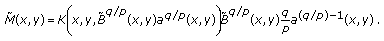
 is nonincreasing in
is nonincreasing in  and using the part (ii) of Lemma 2.2, we can complete the proof by following the proof of (i) with suitable changes. Therefore, the details are omitted here.
and using the part (ii) of Lemma 2.2, we can complete the proof by following the proof of (i) with suitable changes. Therefore, the details are omitted here.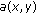 is nondecreasing in
is nondecreasing in 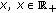 . If
. If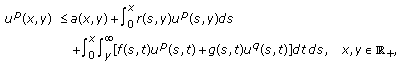
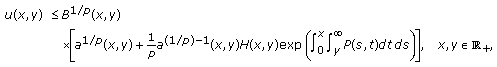
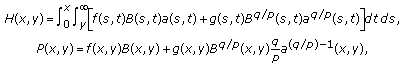
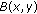 is defined by (2.29).
is defined by (2.29). is nonincreasing in
is nonincreasing in 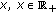 . If
. If
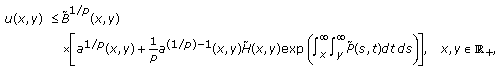

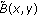 is defined by (25').
is defined by (25').
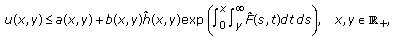
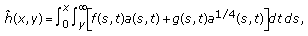
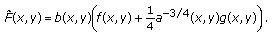
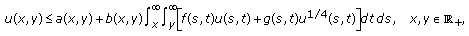

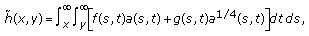
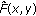 is defined by (2.45).
is defined by (2.45).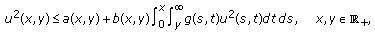
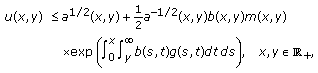
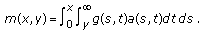
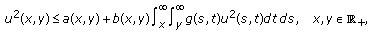
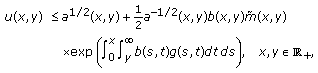
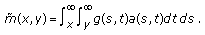
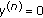 and of the analogous difference equation. Journal of Differential Equations 1984,53(2):234-257. 10.1016/0022-0396(84)90041-X
and of the analogous difference equation. Journal of Differential Equations 1984,53(2):234-257. 10.1016/0022-0396(84)90041-X