Abstract
We study the existence and uniqueness of solutions and nonlocal controllability for the impulsive semilinear nonlocal fuzzy integrodifferential equations in  -dimensional fuzzy vector space
-dimensional fuzzy vector space  by using short-term perturbations techniques and Banach fixed point theorem. This is an extension of the result of Kwun et al. (Kwun et al., 2009) to impulsive system.
by using short-term perturbations techniques and Banach fixed point theorem. This is an extension of the result of Kwun et al. (Kwun et al., 2009) to impulsive system.
Similar content being viewed by others
1. Introduction
The theory of differential equations with discontinuous trajectories during the last twenty years has been to a great extent stimulated by their numerous applications to problem arising in mechanics, electrical engineering, the theory of automatic control, medicine and biology. For the monographs of the theory of impulsive differential equations, see the papers of Bainov and Simenov [1], Lakshmikantham et al. [2] and Samoileuko and Perestyuk [3], where numerous properties of their solutions are studied and detailed bibliographies are given. Rogovchenko [4] followed the ideas of the theory of impulsive differential equations which treats the changes of the state of the evolution process due to a short-term perturbations whose duration can be negligible in comparison with the duration of the process as an instant impulses. In 2001, Lakshmikantham and McRae [5] studied basic results for fuzzy impulsive differential equations. Park et al. [6] studied the existence and uniqueness of fuzzy solutions and controllability for the impulsive semilinear fuzzy integrodifferential equations in one-dimensional fuzzy vector space  . Rodríguez-López [7] studied periodic boundary value problems for impulsive fuzzy differential equations. Fuzzy integrodifferential equations are a field of interest, due to their applicability to the analysis of phenomena with memory where imprecision is inherent. Balasubramaniam and Muralisankar [8] proved the existence and uniqueness of fuzzy solutions for the semilinear fuzzy integrodifferential equation with nonlocal initial condition. They considered the semilinear one-dimensional heat equation on a connected domain
. Rodríguez-López [7] studied periodic boundary value problems for impulsive fuzzy differential equations. Fuzzy integrodifferential equations are a field of interest, due to their applicability to the analysis of phenomena with memory where imprecision is inherent. Balasubramaniam and Muralisankar [8] proved the existence and uniqueness of fuzzy solutions for the semilinear fuzzy integrodifferential equation with nonlocal initial condition. They considered the semilinear one-dimensional heat equation on a connected domain  for material with memory. In one-dimensional fuzzy vector space
for material with memory. In one-dimensional fuzzy vector space  , Park et al. [9] proved the existence and uniqueness of fuzzy solutions and presented the sufficient condition of nonlocal controllability for the following semilinear fuzzy integrodifferential equation with nonlocal initial condition.
, Park et al. [9] proved the existence and uniqueness of fuzzy solutions and presented the sufficient condition of nonlocal controllability for the following semilinear fuzzy integrodifferential equation with nonlocal initial condition.
In [10], Kwun et al. proved the existence and uniqueness of fuzzy solutions for the semilinear fuzzy integrodifferential equations by using successive iteration. In [11], Kwun et al. investigated the continuously initial observability for the semilinear fuzzy integrodifferential equations. Bede and Gal [12] studied almost periodic fuzzy-number-valued functions. Gal and N'Guerekata [13] studied almost automorphic fuzzy-number-valued functions. More recently, Kwun et al. [14] studied the existence and uniqueness of solutions and nonlocal controllability for the semilinear fuzzy integrodifferential equations in  -dimensional fuzzy vector space.
-dimensional fuzzy vector space.
In this paper, we study the existence and uniqueness of solutions and nonlocal controllability for the following impulsive semilinear nonlocal fuzzy integrodifferential equations in  -dimensional fuzzy vector space by using short-term perturbations techniques and Banach fixed point theorem:
-dimensional fuzzy vector space by using short-term perturbations techniques and Banach fixed point theorem:

where  is fuzzy coefficient,
is fuzzy coefficient,  is the set of all upper semicontinuously convex fuzzy numbers on
is the set of all upper semicontinuously convex fuzzy numbers on  with
with  ,
,  and
and  are nonlinear regular fuzzy functions,
are nonlinear regular fuzzy functions,  is a nonlinear continuous function,
is a nonlinear continuous function,  is an
is an  continuous matrix such that
continuous matrix such that  is continuous for
is continuous for  and
and  with
with  ,
,  ,
,  is a control function,
is a control function,  is an initial value and
is an initial value and  are bounded functions,
are bounded functions,  , where
, where  and
and  represent the left and right limits of
represent the left and right limits of  at
at  , respectively.
, respectively.
2. Preliminaries
A fuzzy set  of
of  is a function
is a function  . For each fuzzy set
. For each fuzzy set  , we denote by
, we denote by  for any
for any  its
its  -level set.
-level set.
Let  be fuzzy sets of
be fuzzy sets of  . It is well known that
. It is well known that  for each
for each  implies
implies  .
.
Let  denote the collection of all fuzzy sets of
denote the collection of all fuzzy sets of  that satisfies the following conditions:
that satisfies the following conditions:
-
(1)
 is normal, that is, there exists an
is normal, that is, there exists an  such that
such that  ;
; -
(2)
 is fuzzy convex, that is,
is fuzzy convex, that is, 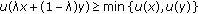 for any
for any 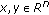 ,
, 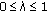 ;
; -
(3)
 is upper semicontinuous, that is,
is upper semicontinuous, that is, 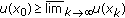 for any
for any 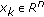
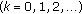 ,
,  ;
; -
(4)
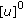 is compact.
is compact.
We call  an
an  -dimension fuzzy number.
-dimension fuzzy number.
Wang et al. [15] defined  -dimensional fuzzy vector space and investigated its properties.
-dimensional fuzzy vector space and investigated its properties.
For any  ,
,  , we call the ordered one-dimension fuzzy number class
, we call the ordered one-dimension fuzzy number class  (i.e., the Cartesian product of one-dimension fuzzy number
(i.e., the Cartesian product of one-dimension fuzzy number  ) an
) an  -dimension fuzzy vector, denote it as
-dimension fuzzy vector, denote it as  , and call the collection of all
, and call the collection of all  -dimension fuzzy vectors (i.e., the Cartesian product
-dimension fuzzy vectors (i.e., the Cartesian product  )
)  -dimensional fuzzy vector space, and denote it as
-dimensional fuzzy vector space, and denote it as  .
.
Definition 2.1 (see [15]).
If  , and
, and  is a hyperrectangle, that is,
is a hyperrectangle, that is,  can be represented by
can be represented by  , that is,
, that is,  for every
for every  , where
, where  with
with  when
when  ,
,  , then we call
, then we call  a fuzzy
a fuzzy  -cell number. We denote the collection of all fuzzy
-cell number. We denote the collection of all fuzzy  -cell numbers by
-cell numbers by  .
.
Theorem 2.2 (see [15]).
For any  with
with 
 , there exists a unique
, there exists a unique  such that
such that  (
( and
and  ). Conversely, for any
). Conversely, for any  with
with  (
(
 and
and  ), there exists a unique
), there exists a unique  such that
such that 
 .
.
Note (see [15]).
Theorem 2.2 indicates that fuzzy  -cell numbers and
-cell numbers and  -dimension fuzzy vectors can represent each other, so
-dimension fuzzy vectors can represent each other, so  and
and  may be regarded as identity. If
may be regarded as identity. If  is the unique
is the unique  -dimension fuzzy vector determined by
-dimension fuzzy vector determined by  , then we denote
, then we denote  .
.
Let  , where
, where  is a fuzzy subset of
is a fuzzy subset of  . Then
. Then  .
.
Definition 2.3 (see [15]).
The complete metric  on
on  is defined by
is defined by

for any  , which satisfies
, which satisfies  .
.
Definition 2.4.
Let  ,
,

Definition 2.5 (see [15]).
The derivative  of a fuzzy process
of a fuzzy process  is defined by
is defined by

provided that equation defines a fuzzy  .
.
Definition 2.6 (see [15]).
The fuzzy integral  ,
,  is defined by
is defined by

provided that the Lebesgue integrals on the right-hand side exist.
3. Existence and Uniqueness
In this section we consider the existence and uniqueness of the fuzzy solution for (1.1) ( ).
).
We define


Then

Instead of (1.1), we consider the following fuzzy integrodifferential equations in  .
.



with fuzzy coefficient  , initial value
, initial value  , and
, and  being a control function. Given nonlinear regular fuzzy functions
being a control function. Given nonlinear regular fuzzy functions  and
and  satisfy global Lipschitz conditions, that is, there exist finite constants
satisfy global Lipschitz conditions, that is, there exist finite constants  such that
such that


for all  ,the nonlinear function
,the nonlinear function  is continuous and satisfies the Lipschitz condition
is continuous and satisfies the Lipschitz condition

for all  ,
,  is a finite positive constant.
is a finite positive constant.
Definition 3.1.
The fuzzy process  with
with  -level set
-level set  is a fuzzy solution of (3.4) and (3.5) without nonhomogeneous term if and only if
is a fuzzy solution of (3.4) and (3.5) without nonhomogeneous term if and only if

For the sequel, we need the following assumption:
(H1) is a fuzzy number satisfying, for
is a fuzzy number satisfying, for  ,
,  , the equation
, the equation

where

and 
 is continuous with
is continuous with  ,
,  , for all
, for all  .
.
In order to define the solution of (3.4)–(3.6), we will consider the space  =
=  and there exist
and there exist  and
and  with
with 
Let  .
.
Lemma 3.2.
If  is an integral solution of (3.4)–(3.6)
is an integral solution of (3.4)–(3.6)  , then
, then  is given by
is given by

Proof.
Let  be a solution of (3.4)–(3.6). Define
be a solution of (3.4)–(3.6). Define  . Then we have that
. Then we have that

Consider  . Then integrating the previous equation, we have
. Then integrating the previous equation, we have

For  ,
,

or

Now for  we have that
we have that

Then

if and only if

Hence

which proves the lemma.
Assume the following:
(H2)there exists  such that
such that

where  ;
;
(H3)

Theorem 3.3.
Let  . If hypotheses (H1)–(H3) are hold, then, for every
. If hypotheses (H1)–(H3) are hold, then, for every  , (3.13) has a unique fuzzy solution
, (3.13) has a unique fuzzy solution  .
.
Proof.
For each  and
and  , define
, define  by
by

Thus,  is continuous, so
is continuous, so  is a mapping from
is a mapping from  into itself. By Definitions 2.3 and 2.4, some properties of
into itself. By Definitions 2.3 and 2.4, some properties of  and inequalities (3.7), (3.8), and (3.9), we have the following inequalities. For
and inequalities (3.7), (3.8), and (3.9), we have the following inequalities. For  ,
,

Therefore

Hence

By hypothesis (H3),  is a contraction mapping. Using the Banach fixed point theorem, (3.13) has a unique fixed point
is a contraction mapping. Using the Banach fixed point theorem, (3.13) has a unique fixed point  .
.
4. Nonlocal Controllability
In this section, we show the nonlocal controllability for the control system (1.1).
The control system (1.1) is related to the following fuzzy integral system:

Definition 4.1.
Equations (1.1)–(3) are nonlocal controllable. Then there exists  such that the fuzzy solution
such that the fuzzy solution  for (4.1) as
for (4.1) as 
 , where
, where  , is target set.
, is target set.
Define the fuzzy mapping  by
by

where  is closed support of
is closed support of  . Then there exists
. Then there exists

such that

Then there exists 
 such that
such that

We assume that  are bijective mappings.
are bijective mappings.
We can introduce  -level set of
-level set of  of (4.1):
of (4.1):

Then substituting this expression into (4.1) yields  -level of
-level of  .
.
For each  ,
,

Therefore

We now set

where the fuzzy mapping  satisfies the previous statements.
satisfies the previous statements.
Notice that  , which means that the control
, which means that the control  steers (4.9) from the origin to
steers (4.9) from the origin to  in time
in time  provided we can obtain a fixed point of the operator
provided we can obtain a fixed point of the operator  .
.
(H4)Assume that the linear system of (4.9)  is controllable.
is controllable.
Theorem 4.2.
Suppose that hypotheses (H1)–(H4) are satisfied. Then (4.9) is nonlocal controllable.
Proof.
We can easily check that  is continuous function from
is continuous function from  to itself. By Definitions 2.3 and 2.4, some properties of
to itself. By Definitions 2.3 and 2.4, some properties of  , and inequalities (3.7), (3.8), and (3.9), we have following inequalities. For any
, and inequalities (3.7), (3.8), and (3.9), we have following inequalities. For any  ,
,

Therefore

Hence

By hypothesis (H3),  is a contraction mapping. Using the Banach fixed point theorem, (4.9) has a unique fixed point
is a contraction mapping. Using the Banach fixed point theorem, (4.9) has a unique fixed point  .
.
5. Example
Consider the two semilinear one-dimensional heat equations on a connected domain  for material with memory on
for material with memory on  boundary condition
boundary condition

and with initial conditions

where  ,
,

Let  be the internal energy and
be the internal energy and

be the external heat withmemory.

is impulsive effect at 
 .
.
Let

then the balance equations become

The  -level sets of fuzzy numbers are the following
-level sets of fuzzy numbers are the following
 ,
,  for all
for all  . Then
. Then  -level set of
-level set of  is
is

Further, we have

where  ,
,  , and
, and  satisfy inequalities (3.7), (3.8), and (3.9), respectively. Choose
satisfy inequalities (3.7), (3.8), and (3.9), respectively. Choose  such that
such that  . Then all conditions stated in Theorem 3.3 are satisfied, so the problem (5.7) has a unique fuzzy solution.
. Then all conditions stated in Theorem 3.3 are satisfied, so the problem (5.7) has a unique fuzzy solution.
Let target set be  . The
. The  -level set of fuzzy numbersis
-level set of fuzzy numbersis
 .
.
From the definition of fuzzy solution,

where  .
.
Thus the  -levels of
-levels of 

Then  -level of
-level of  is
is

Similarly,

Hence

Then all the conditions stated in Theorem 4.2 are satisfied, so the system (5.7) is nonlocal controllable on  .
.
References
Bainov DD, Simenov PS: Impulsive Differential Equations: Periodic Solutions and Applications. Longman, Harlow, UK; 1993.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Singapore; 1989:xii+273.
Samoileuko AM, Perestyuk NA: Impulsive Differential Equations, Series on Advances in Mathematics for Applied Sciences. Volume 28. World Scientific, Singapore; 1995:xii+230.
Rogovchenko YV: Impulsive evolution systems: main results and new trends. Dynamics of Continuous, Discrete and Impulsive Systems 1997,3(1):57-88.
Lakshmikantham V, McRae FA: Basic results for fuzzy impulsive differential equations. Mathematical Inequalities & Applications 2001,4(2):239-246.
Park JH, Park JS, Ahn YC, Kwun YC: Controllability for the impulsive semilinear fuzzy integrodifferential equations. Advances in Soft Computing 2007, 40: 704-713. 10.1007/978-3-540-71441-5_76
Rodríguez-López R: Periodic boundary value problems for impulsive fuzzy differential equations. Fuzzy Sets and Systems 2008,159(11):1384-1409. 10.1016/j.fss.2007.09.005
Balasubramaniam P, Muralisankar S: Existence and uniqueness of fuzzy solution for semilinear fuzzy integrodifferential equations with nonlocal conditions. Computers & Mathematics with Applications 2004,47(6-7):1115-1122. 10.1016/S0898-1221(04)90091-0
Park JH, Park JS, Kwun YC: Controllability for the semilinear fuzzy integrodifferential equations with nonlocal conditions. Proceedings of the 3rd International Conference on Fuzzy Systems and Knowledge Discovery (FSKD '06), 2006, Lecture Notes in Artificial Intelligence 4223: 221-230.
Kwun YC, Kim MJ, Lee BY, Park JH: Existence of solutions for the semilinear fuzzy integrodifferential equations using by succesive iteration. Journal of Korean Institute of Intelligent Systems 2008, 18: 543-548. 10.5391/JKIIS.2008.18.4.543
Kwun YC, Kim MJ, Park JS, Park JH: Continuously initial observability for the semilinear fuzzy integrodifferential equations. Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD '08), 2008 1: 225-229.
Bede B, Gal SG: Almost periodic fuzzy-number-valued functions. Fuzzy Sets and Systems 2004,147(3):385-403. 10.1016/j.fss.2003.08.004
Gal SG, N'Guerekata GM: Almost automorphic fuzzy-number-valued functions. Journal of Fuzzy Mathematics 2005,13(1):185-208.
Kwun YC, Kim JS, Park MJ, Park JH:Nonlocal controllability for the semilinear fuzzy integrodifferential equations in
 -dimensional fuzzy vector space. Advances in Difference Equations 2009, 2009:-16.
-dimensional fuzzy vector space. Advances in Difference Equations 2009, 2009:-16.Wang G, Li Y, Wen C:On fuzzy
 -cell numbers and
-cell numbers and  -dimension fuzzy vectors. Fuzzy Sets and Systems 2007,158(1):71-84. 10.1016/j.fss.2006.09.006
-dimension fuzzy vectors. Fuzzy Sets and Systems 2007,158(1):71-84. 10.1016/j.fss.2006.09.006
Acknowledgment
This study was supported by research funds from Dong-A University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kwun, Y., Kim, J., Park, M. et al. Controllability for the Impulsive Semilinear Nonlocal Fuzzy Integrodifferential Equations in  -Dimensional Fuzzy Vector Space.
Adv Differ Equ 2010, 983483 (2010). https://doi.org/10.1155/2010/983483
-Dimensional Fuzzy Vector Space.
Adv Differ Equ 2010, 983483 (2010). https://doi.org/10.1155/2010/983483
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/983483



 is normal, that is, there exists an
is normal, that is, there exists an  such that
such that  ;
; is fuzzy convex, that is,
is fuzzy convex, that is, 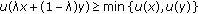 for any
for any 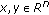 ,
, 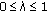 ;
; is upper semicontinuous, that is,
is upper semicontinuous, that is, 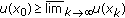 for any
for any 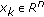
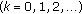 ,
,  ;
;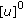 is compact.
is compact. -dimensional fuzzy vector space. Advances in Difference Equations 2009, 2009:-16.
-dimensional fuzzy vector space. Advances in Difference Equations 2009, 2009:-16. -cell numbers and
-cell numbers and  -dimension fuzzy vectors. Fuzzy Sets and Systems 2007,158(1):71-84. 10.1016/j.fss.2006.09.006
-dimension fuzzy vectors. Fuzzy Sets and Systems 2007,158(1):71-84. 10.1016/j.fss.2006.09.006