Abstract
We investigate the singular differential equation  on the half-line [
on the half-line [ ), where
), where  satisfies the local Lipschitz condition on
satisfies the local Lipschitz condition on  and has at least two simple zeros. The function
and has at least two simple zeros. The function  is continuous on [
is continuous on [ ) and has a positive continuous derivative on (
) and has a positive continuous derivative on ( ) and
) and  . We bring additional conditions for
. We bring additional conditions for  and
and  under which the equation has oscillatory solutions with decreasing amplitudes.
under which the equation has oscillatory solutions with decreasing amplitudes.
Similar content being viewed by others
1. Introduction
We study the equation

on the half-line  , where
, where


Equation (1.1) is singular at  because
because  . If
. If  in (1.1) fulfils moreover assumptions
in (1.1) fulfils moreover assumptions



then (1.1) generalizes equations which appear in hydrodynamics or in the nonlinear field theory [1–5].
Definition 1.1.
A function  which has continuous second derivative on
which has continuous second derivative on  and satisfies (1.1) for all
and satisfies (1.1) for all  is called a solution of (1.1).
is called a solution of (1.1).
Consider  and the initial conditions
and the initial conditions

The initial value problem (1.1), (1.7) has been investigated, for example, in [6–12]. In particular in [10] it was proved that for each negative  there exists a unique solution of problem (1.1), (1.7) under the assumptions (1.2)–(1.6). Consider such solution
there exists a unique solution of problem (1.1), (1.7) under the assumptions (1.2)–(1.6). Consider such solution  and denote
and denote

Definition 1.2.
If  (
( or
or  ), then
), then  is called a damped solution (a homoclinic solution or an escape solution) of problem (1.1), (1.7).
is called a damped solution (a homoclinic solution or an escape solution) of problem (1.1), (1.7).
In [10, 12] these three types of solutions of problem (1.1), (1.7) have been studied, and the existence of each type has been proved for sublinear or linear asymptotic behaviour of  near
near  . In [11],
. In [11],  has been supposed to have a zero
has been supposed to have a zero  . Here we generalize and extend the results of [10–12] concerning damped solutions. We prove their existence under weaker assumptions than in the above papers. Moreover, we bring conditions under which each damped solution is oscillatory; that is, it has an unbounded set of isolated zeros.
. Here we generalize and extend the results of [10–12] concerning damped solutions. We prove their existence under weaker assumptions than in the above papers. Moreover, we bring conditions under which each damped solution is oscillatory; that is, it has an unbounded set of isolated zeros.
We replace assumptions (1.4)–(1.6) by the following ones.
There exist  ,
,  ,
,  such that
such that


( is possible).
is possible).
2. Damped Solutions
Theorem 2.1 (Existence and uniqueness).
Assume that (1.2), (1.3), (1.9), and (1.10) hold and let  . Then problem (1.1), (1.7) has a unique solution
. Then problem (1.1), (1.7) has a unique solution  , and moreover the solution
, and moreover the solution  satisfies
satisfies

Proof.
Step 1.
Put

We will study the auxiliary differential equation:

By virtue of (1.2) we find the Lipschitz constant  for
for  on
on  , and due to (1.2), (1.10), and (2.2), we find
, and due to (1.2), (1.10), and (2.2), we find  such that
such that

Put  for
for  . Having in mind (1.3), we see that
. Having in mind (1.3), we see that  is increasing and so
is increasing and so

Consequently we can choose  such that
such that

Consider the Banach space  (with the maximum norm) and define an operator
(with the maximum norm) and define an operator  by
by

Using (2.4) and (2.6), we have

that is  maps the ball
maps the ball  to itself. Due to (2.2) and the choice of
to itself. Due to (2.2) and the choice of  , we have for
, we have for  ,
, 

Hence  is a contraction on
is a contraction on  , and the Banach fixed point theorem yields a unique fixed point
, and the Banach fixed point theorem yields a unique fixed point  of
of  .
.
Step 2.
The fixed point  of Step 1 fulfils
of Step 1 fulfils

Hence  satisfies (2.3) on
satisfies (2.3) on  . Finally, (2.4) and (2.5) yield
. Finally, (2.4) and (2.5) yield

Consequently  fulfils (1.7). Choose an arbitrary
fulfils (1.7). Choose an arbitrary  . Then, by (2.5) and (2.10),
. Then, by (2.5) and (2.10),

Having in mind that  ,
,  can be (uniquely) extended as a function satisfying (2.3) onto
can be (uniquely) extended as a function satisfying (2.3) onto  . Since
. Since  is arbitrary,
is arbitrary,  can be extended onto
can be extended onto  as a solution of (2.3). We have proved that problem (2.3), (1.7) has a unique solution.
as a solution of (2.3). We have proved that problem (2.3), (1.7) has a unique solution.
Step 3.
According to Step 2 we have

Multiplying (2.13) by  and integrating between
and integrating between  and
and  , we get
, we get

Put

So,(2.14) has the form

Let  for some
for some  . Then (2.16) yields
. Then (2.16) yields  which is not possible because
which is not possible because  is decreasing on
is decreasing on  by (1.9) and (2.2). Therefore
by (1.9) and (2.2). Therefore  for
for  . Consequently, due to (2.2),
. Consequently, due to (2.2),  is a solution of (1.1).
is a solution of (1.1).
Step 4.
Assume that there exists another solution  of problem (1.1), (1.7). Then we can prove similarly as in Step 3 that
of problem (1.1), (1.7). Then we can prove similarly as in Step 3 that  for
for  . This implies that
. This implies that  is also a solution of problem (2.3), (1.7) and by Step 2,
is also a solution of problem (2.3), (1.7) and by Step 2,  . We have proved that problem (1.1), (1.7) has a unique solution.
. We have proved that problem (1.1), (1.7) has a unique solution.
Lemma 2.2.
Let  and let
and let  be a solution of (1.1). Assume that there exists
be a solution of (1.1). Assume that there exists  such that
such that

Then  for all
for all  .
.
Proof.
We see that the constant function  is a solution of (1.1). Let
is a solution of (1.1). Let  be a solution of (1.1) satisfying (2.17) and let
be a solution of (1.1) satisfying (2.17) and let  for some
for some  . Then the regular initial problem (1.1), (2.17) has two different solutions
. Then the regular initial problem (1.1), (2.17) has two different solutions  and
and  , which contradicts (1.2).
, which contradicts (1.2).
Remark 2.3.
Let us put

Due to (1.2) and (1.9) we see that  is continuous on
is continuous on  , decreasing and positive on
, decreasing and positive on  , increasing and positive on
, increasing and positive on  . Therefore we can define
. Therefore we can define  by
by

( .
.
Theorem 2.4 (Existence of damped solutions).
Assume that (1.2), (1.3), (1.9), and (1.10) hold. Let  be given by (2.19), and assume that
be given by (2.19), and assume that  is a solution of problem (1.1), (1.7) with
is a solution of problem (1.1), (1.7) with  . Then
. Then  is a damped solution.
is a damped solution.
Proof.
Since  , we can find
, we can find  such that
such that

Assume on the contrary that  is not damped, that is,
is not damped, that is,

Then, according to Lemma 2.2, there exists  such that
such that

By (1.1), (1.3), and (1.9) we have  on
on  . So,
. So,  is increasing and positive on
is increasing and positive on  and hence
and hence  on
on  . Assumption (2.21) implies that there exists
. Assumption (2.21) implies that there exists  such that
such that

Since  fulfils (1.1), we have
fulfils (1.1), we have

Multiplying (2.24) by  and integrating between
and integrating between  and
and  we get
we get

This contradicts (2.20).
3. Oscillatory Solutions
In this section we assume that, in addition to our basic assumptions (1.2), (1.3), (1.9), and (1.10), the following conditions are fulfilled:


Then the next lemmas can be proved.
Lemma 3.1.
Let  be a solution of problem (1.1), (1.7) with
be a solution of problem (1.1), (1.7) with  . Then there exists
. Then there exists  such that
such that

Proof.
Step 1.
Assume that such  does not exist. Then
does not exist. Then

Hence (1.1), (1.7), and (1.9) yield  and
and  on
on  . Therefore
. Therefore  is increasing on
is increasing on  and
and

Multiplying (2.24) by  and integrating between
and integrating between  and
and  , we get due to (2.18)
, we get due to (2.18)

Letting  , we get
, we get

Since the function  is positive and increasing, it follows that there exists
is positive and increasing, it follows that there exists  . If
. If  , then
, then  contrary to (3.5). Consequently,
contrary to (3.5). Consequently,

Letting  in (2.24), we get by (1.3), (1.9), and (3.5)
in (2.24), we get by (1.3), (1.9), and (3.5)

Due to (3.8), we conclude that  and hence
and hence  . We have proved that if
. We have proved that if  fulfilling (3.3) does not exist, then
fulfilling (3.3) does not exist, then

Step 2.
We define a function

By (1.3) and (3.2), we have  ,
,



Due to (1.3), (3.1), (3.10) and (3.14) there exist  and
and  such that
such that

Due to (3.4), (3.11), (3.13), and (3.15), we get

Thus,  is increasing on
is increasing on  and has the limit
and has the limit

If  , then
, then  , which contradicts (3.4) and (3.11). If
, which contradicts (3.4) and (3.11). If  , then
, then  on
on  and
and

In view of (3.16) we can see that

We get  which contradicts
which contradicts  . The obtained contradictions imply that (3.4) cannot occur and hence
. The obtained contradictions imply that (3.4) cannot occur and hence  satisfying (3.3) must exist.
satisfying (3.3) must exist.
Corollary 3.2.
Let  be a solution of problem (1.1), (1.7) with
be a solution of problem (1.1), (1.7) with  . Further assume that there exist
. Further assume that there exist  and
and  such that
such that

Then there exists  such that
such that

Proof.
We can argue as in the proof of Lemma 3.1 working with  and
and  instead of
instead of  and
and  .
.
Lemma 3.3.
Let  be a solution of problem (1.1), (1.7) with
be a solution of problem (1.1), (1.7) with  . Further assume that there exist
. Further assume that there exist  and
and  such that
such that

Then there exists  such that
such that

Proof.
We argue similarly as in the proof of Lemma 3.1.
Step 1.
Assume that such  does not exist. Then
does not exist. Then

By (1.1), (1.7), and (1.9) we deduce  on
on  and
and

Multiplying (2.24) by  , integrating between
, integrating between  and
and  , and using (2.18), we obtain
, and using (2.18), we obtain

and we derive as in the proof of Lemma 3.1 that (3.10) holds.
Step 2.
We define  by (3.11) and get (3.13) for
by (3.11) and get (3.13) for  . As in the proof of Lemma 3.1 we find
. As in the proof of Lemma 3.1 we find  and
and  satisfying (3.15). Due to (3.24), (3.11), (3.13), and (3.15) we get
satisfying (3.15). Due to (3.24), (3.11), (3.13), and (3.15) we get

So,  is decreasing on
is decreasing on  and
and  . If
. If  , then
, then  which contradicts (3.24) and (3.11). If
which contradicts (3.24) and (3.11). If  , then
, then  on
on  and
and

In view of (3.27) we can see that

We get  contrary to
contrary to  . The obtained contradictions imply that (3.24) cannot occur and that
. The obtained contradictions imply that (3.24) cannot occur and that  satisfying (3.23) must exist.
satisfying (3.23) must exist.
Theorem 3.4.
Assume that (1.2), (1.3), (1.9), (1.10), (3.1), and (3.2) hold. Let  be a solution of problem (1.1), (1.7) with
be a solution of problem (1.1), (1.7) with  . If
. If  is a damped solution, then
is a damped solution, then  is oscillatory and its amplitudes are decreasing.
is oscillatory and its amplitudes are decreasing.
Proof.
Let  be a damped solution. By (2.1) and Definition 1.2, we can find
be a damped solution. By (2.1) and Definition 1.2, we can find  such that
such that

Step 1.
Lemma 3.1 yields  satisfying (3.3). Hence there exists a maximal interval
satisfying (3.3). Hence there exists a maximal interval  such that
such that  on
on  . Let
. Let  . Then, by (3.30), we get
. Then, by (3.30), we get  ,
,  on
on  and
and

By (1.1), (1.3), and (1.9), we have  on
on  . So
. So  and
and  are decreasing on
are decreasing on  and, due to (3.31),
and, due to (3.31),

Letting  in (2.24) and using (1.3), (1.9), and (3.31), we get
in (2.24) and using (1.3), (1.9), and (3.31), we get

which contradicts (3.32). Therefore  and there exists
and there exists  such that (3.22) holds. Lemma 3.3 yields
such that (3.22) holds. Lemma 3.3 yields  satisfying (3.23). Therefore
satisfying (3.23). Therefore  has just one positive local maximum
has just one positive local maximum  between its first zero
between its first zero  and second zero
and second zero  .
.
Step 2.
By (3.23) there exists a maximal interval  , where
, where  . Let
. Let  . Then, by (3.30), we have
. Then, by (3.30), we have  ,
,  on
on  , and
, and

By (1.1), (1.3), and (1.9), we get  on
on  and so
and so  is increasing on
is increasing on  . Since
. Since  , we deduce that
, we deduce that  is increasing on
is increasing on  and, by (3.34), we get (3.32). Letting
and, by (3.34), we get (3.32). Letting  in (1.1) and using (1.3), (1.9), and (3.34), we get
in (1.1) and using (1.3), (1.9), and (3.34), we get

which contradicts (3.32). Therefore  and there exists
and there exists  such that (3.20) holds. Corollary 3.2 yields
such that (3.20) holds. Corollary 3.2 yields  satisfying (3.21). Therefore
satisfying (3.21). Therefore  has just one negative minimum
has just one negative minimum  between its second zero
between its second zero  and third zero
and third zero  .
.
Step 3.
We can continue as in Step 1 and Step 2 and get the sequences  and
and  of local maxima and local minima of
of local maxima and local minima of  attained at
attained at  and
and  , respectively. Now, put
, respectively. Now, put  ,
,  and write (1.1) as a system
and write (1.1) as a system

Consider  of (2.18) and define a Lyapunov function
of (2.18) and define a Lyapunov function  by
by

where  . By Remark 2.3, we see that
. By Remark 2.3, we see that  and
and  on
on  . By (3.6) and (3.37), we have
. By (3.6) and (3.37), we have 

Therefore

By (3.30),  for
for  . We see that
. We see that  is positive and decreasing (for the damped solution
is positive and decreasing (for the damped solution  ) and hence
) and hence

So, sequences  and
and  are decreasing:
are decreasing:

for  and
and

Further, due to Remark 2.3, the sequence  is decreasing and the sequence
is decreasing and the sequence  is increasing. Consequently,
is increasing. Consequently,

Remark 3.5.
There are two cases for the number  from the proof of Theorem 3.4:
from the proof of Theorem 3.4:  and
and  . Denote
. Denote

If  , then
, then  and hence
and hence  , that is,
, that is,  .
.
Let  . Consider an arbitrary sequence
. Consider an arbitrary sequence  such that
such that  . By (3.40) we have
. By (3.40) we have  . By (3.30) and (3.6), the sequence
. By (3.30) and (3.6), the sequence  is bounded and so there exists a subsequence
is bounded and so there exists a subsequence

such that  , where
, where  is a point of the level curve:
is a point of the level curve:

Note that

Theorem 3.6 (Existence of oscillatory solutions).
Assume that (1.2), (1.3), (1.9), (1.10), (3.1), and (3.2) hold. Let  be given by (2.19) and let
be given by (2.19) and let  be a solution of problem (1.1), (1.7) with
be a solution of problem (1.1), (1.7) with  . Then
. Then  is an oscillatory solution with decreasing amplitudes.
is an oscillatory solution with decreasing amplitudes.
Proof.
The assertion follows from Theorems 2.4 and 3.4.
Remark 3.7.
The assumption (1.10) in Theorem 3.6 can be omitted, because it has no influence on the existence of oscillatory solutions. It follows from the fact that (1.10) imposes conditions on the function values of the function  for arguments greater than
for arguments greater than  ; however, the function values of oscillatory solutions are lower than this constant
; however, the function values of oscillatory solutions are lower than this constant  . This condition (used only in Theorem 2.1) guaranteed the existence of solution of each problem (1.1), (1.7) for each
. This condition (used only in Theorem 2.1) guaranteed the existence of solution of each problem (1.1), (1.7) for each  on the whole half-line, which simplified the investigation of the problem.
on the whole half-line, which simplified the investigation of the problem.
References
Dell'Isola F, Gouin H, Rotoli G: Nucleation of spherical shell-like interfaces by second gradient theory: numerical simulations. European Journal of Mechanics 1996,15(4):545-568.
Derrick GH: Comments on nonlinear wave equations as models for elementary particles. Journal of Mathematical Physics 1964, 5: 1252-1254. 10.1063/1.1704233
Gouin H, Rotoli G: An analytical approximation of density profile and surface tension of microscopic bubbles for Van Der Waals fluids. Mechanics Research Communications 1997,24(3):255-260. 10.1016/S0093-6413(97)00022-0
Kitzhofer G, Koch O, Lima P, Weinmüller E: Efficient numerical solution of the density profile equation in hydrodynamics. Journal of Scientific Computing 2007,32(3):411-424. 10.1007/s10915-007-9141-0
Lima PM, Konyukhova NB, Sukov AI, Chemetov NV: Analytical-numerical investigation of bubble-type solutions of nonlinear singular problems. Journal of Computational and Applied Mathematics 2006,189(1-2):260-273. 10.1016/j.cam.2005.05.004
Berestycki H, Lions P-L, Peletier LA:An ODE approach to the existence of positive solutions for semilinear problems in
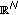 . Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012Bonheure D, Gomes JM, Sanchez L: Positive solutions of a second-order singular ordinary differential equation. Nonlinear Analysis: Theory, Methods & Applications 2005,61(8):1383-1399. 10.1016/j.na.2005.02.029
Conti M, Merizzi L, Terracini S:Radial solutions of superlinear equations on
 . I. A global variational approach. Archive for Rational Mechanics and Analysis 2000,153(4):291-316. 10.1007/s002050050015
. I. A global variational approach. Archive for Rational Mechanics and Analysis 2000,153(4):291-316. 10.1007/s002050050015Koch O, Kofler P, Weinmüller EB: Initial value problems for systems of ordinary first and second order differential equations with a singularity of the first kind. Analysis 2001,21(4):373-389.
Rachůnková I, Tomeček J: Bubble-type solutions of nonlinear singular problems. Mathematical and Computer Modelling 2010,51(5-6):658-669. 10.1016/j.mcm.2009.10.042
Rachůnková I, Tomeček J: Strictly increasing solutions of a nonlinear singular differential equation arising in hydrodynamics. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):2114-2118. 10.1016/j.na.2009.10.011
Rachůnková I, Tomeček J: Homoclinic solutions of singular nonautonomous second-order differential equations. Boundary Value Problems 2009, 2009:-21.
Acknowledgment
This work was supported by the Council of Czech Government MSM 6198959214.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rachůnková, I., Tomeček, J. & Stryja, J. Oscillatory Solutions of Singular Equations Arising in Hydrodynamics. Adv Differ Equ 2010, 872160 (2010). https://doi.org/10.1155/2010/872160
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/872160



 . Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012 . I. A global variational approach. Archive for Rational Mechanics and Analysis 2000,153(4):291-316. 10.1007/s002050050015
. I. A global variational approach. Archive for Rational Mechanics and Analysis 2000,153(4):291-316. 10.1007/s002050050015