Abstract
We derive eight basic identities of symmetry in three variables related to Euler polynomials and alternating power sums. These and most of their corollaries are new, since there have been results only about identities of symmetry in two variables. These abundances of symmetries shed new light even on the existing identities so as to yield some further interesting ones. The derivations of identities are based on the  -adic integral expression of the generating function for the Euler polynomials and the quotient of integrals that can be expressed as the exponential generating function for the alternating power sums.
-adic integral expression of the generating function for the Euler polynomials and the quotient of integrals that can be expressed as the exponential generating function for the alternating power sums.
Similar content being viewed by others
1. Introduction and Preliminaries
Let  be a fixed odd prime. Throughout this paper,
be a fixed odd prime. Throughout this paper,  will, respectively, denote the ring of
will, respectively, denote the ring of  -adic integers, the field of
-adic integers, the field of  -adic rational numbers, and the completion of the algebraic closure of
-adic rational numbers, and the completion of the algebraic closure of  . For a continuous function
. For a continuous function  , the
, the  -adic fermionic integral of
-adic fermionic integral of  is defined by
is defined by

Then it is easy to see that

Let  be the normalized absolute value of
be the normalized absolute value of  , such that
, such that  , and let
, and let

Then, for each fixed  , the function
, the function  is analytic on
is analytic on  , and by applying (1.2) to this
, and by applying (1.2) to this  , we get the
, we get the  -adic integral expression of the generating function for Euler numbers
-adic integral expression of the generating function for Euler numbers  :
:

So we have the following  -adic integral expression of the generating function for the Euler polynomials
-adic integral expression of the generating function for the Euler polynomials  :
:

Let  , denote the alternating
, denote the alternating  th power sum of the first
th power sum of the first  nonnegative integers, namely,
nonnegative integers, namely,

In particular,

From (1.4) and (1.6), one easily derives the following identities: for any odd positive integer  ,
,

In what follows, we will always assume that the  -adic fermionic integrals of the various exponential functions on
-adic fermionic integrals of the various exponential functions on  are defined for
are defined for  (cf., (1.3)), and therefore it will not be mentioned.
(cf., (1.3)), and therefore it will not be mentioned.
Many authors have done much work on identities of symmetry involving Bernoulli polynomials or Euler polynomials or  -Bernoulli polynomials or
-Bernoulli polynomials or  -Euler polynomials. We let the reader refer to the papers in [1–20]. In connection with Bernoulli polynomials and power sums, these results were generalized in [21] to obtain identities of symmetry involving three variables in contrast to the previous works involving just two variables.
-Euler polynomials. We let the reader refer to the papers in [1–20]. In connection with Bernoulli polynomials and power sums, these results were generalized in [21] to obtain identities of symmetry involving three variables in contrast to the previous works involving just two variables.
In this paper, we will produce 8 basic identities of symmetry in three variables  ,
,  ,
,  related to Euler polynomials and alternating power sums (cf., (4.8), (4.9), (4.12), (4.16), (4.20), (4.23), (4.25), and (4.26)). These and most of their corollaries seem to be new, since there have been results only about identities of symmetry in two variables in the literature. These abundances of symmetries shed new light even on the existing identities. For instance, it has been known that (1.9) and (1.10) are equal and (1.11) and (1.12) are so (cf., [3, Theorems
related to Euler polynomials and alternating power sums (cf., (4.8), (4.9), (4.12), (4.16), (4.20), (4.23), (4.25), and (4.26)). These and most of their corollaries seem to be new, since there have been results only about identities of symmetry in two variables in the literature. These abundances of symmetries shed new light even on the existing identities. For instance, it has been known that (1.9) and (1.10) are equal and (1.11) and (1.12) are so (cf., [3, Theorems  ]). In fact, (1.9)–(1.12) are all equal, as they can be derived from one and the same
]). In fact, (1.9)–(1.12) are all equal, as they can be derived from one and the same  -adic integral. Perhaps, this was neglected to mention in [3]. Also, we have a bunch of new identities in (1.13)–(1.16). All of these were obtained as corollaries (cf., Corollary 4.9, 4.12, 4.15) to some of the basic identities by specializing the variable
-adic integral. Perhaps, this was neglected to mention in [3]. Also, we have a bunch of new identities in (1.13)–(1.16). All of these were obtained as corollaries (cf., Corollary 4.9, 4.12, 4.15) to some of the basic identities by specializing the variable  as 1. Those would not be unearthed if more symmetries had not been available.
as 1. Those would not be unearthed if more symmetries had not been available.
Let  ,
,  be any odd positive integers. Then we have
be any odd positive integers. Then we have








The derivations of identities will be based on the  -adic integral expression of the generating function for the Euler polynomials in (1.5) and the quotient of integrals in (1.8) that can be expressed as the exponential generating function for the alternating power sums. We indebted this idea to the paper in [3].
-adic integral expression of the generating function for the Euler polynomials in (1.5) and the quotient of integrals in (1.8) that can be expressed as the exponential generating function for the alternating power sums. We indebted this idea to the paper in [3].
2. Several Types of Quotients of Fermionic Integrals
Here we will introduce several types of quotients of  -adic fermionic integrals on
-adic fermionic integrals on  or
or  from which some interesting identities follow owing to the built-in symmetries in
from which some interesting identities follow owing to the built-in symmetries in  ,
,  ,
,  . In the following,
. In the following,  ,
,  ,
,  are all positive integers and all of the explicit expressions of integrals in (2.2), (2.4), (2.6), and (2.8) are obtained from the identity in (1.4).
are all positive integers and all of the explicit expressions of integrals in (2.2), (2.4), (2.6), and (2.8) are obtained from the identity in (1.4).
(a)Type (for
(for ). One has
). One has


(b)Type (for
(for ). One has
). One has


(c-0)Type . One has
. One has


(c-1)Type . One has
. One has


All of the above  -adic integrals of various types are invariant under all permutations of
-adic integrals of various types are invariant under all permutations of  as one can see either from
as one can see either from  -adic integral representations in (2.1), (2.3), (2.5), and (2.7) or from their explicit evaluations in (2.2), (2.4), (2.6), and (2.8).
-adic integral representations in (2.1), (2.3), (2.5), and (2.7) or from their explicit evaluations in (2.2), (2.4), (2.6), and (2.8).
3. Identities for Euler Polynomials
In the following  are all odd positive integers except for (a-0) and (c-0), where they are any positive integers.
are all odd positive integers except for (a-0) and (c-0), where they are any positive integers.
(a-0)First, let us consider Type  , for each
, for each  The following results can be easily obtained from (1.5) and (1.8):
The following results can be easily obtained from (1.5) and (1.8):

where the inner sum is over all nonnegative integers  , with
, with  , and
, and

(a-1)Here we write  in two different ways:
in two different ways:
(1)One has


(2)Invoking (1.8), (3.3) can also be written as

(a-2)Here we write  in three different ways:
in three different ways:
(1)One has


(2)Invoking (1.8), (3.6) can also be written as


(3)Invoking (1.8) once again, (3.8) can be written as

(a-3) One has

-
(b)
For Type
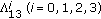 , we may consider the analogous things to the ones in (a-0), (a-1), (a-2), and (a-3). However, these do not lead us to new identities. Indeed, if we substitute
, we may consider the analogous things to the ones in (a-0), (a-1), (a-2), and (a-3). However, these do not lead us to new identities. Indeed, if we substitute 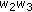 ,
, 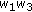 ,
, 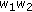 , respectively, for
, respectively, for  in (2.1), this amounts to replacing
in (2.1), this amounts to replacing 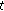 by
by  in (2.3). So, upon replacing
in (2.3). So, upon replacing 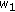 ,
, 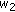 ,
, 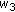 , respectively, by
, respectively, by 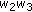 ,
, 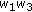 ,
, 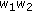 , and then dividing by
, and then dividing by 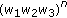 , in each of the expressions of Theorem 4.1 through Corollary 4.15, we will get the corresponding symmetric identities for Type
, in each of the expressions of Theorem 4.1 through Corollary 4.15, we will get the corresponding symmetric identities for Type 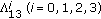 .
.
(c-0)One has

(c-1)One has

4. Main Theorems
As we noted earlier in the last paragraph of Section 2, the various types of quotients of  -adic fermionic integrals are invariant under any permutation of
-adic fermionic integrals are invariant under any permutation of  ,
,  ,
,  . So the corresponding expressions in Section 3 are also invariant under any permutation of
. So the corresponding expressions in Section 3 are also invariant under any permutation of  ,
,  ,
,  . Thus our results about identities of symmetry will be immediate consequences of this observation.
. Thus our results about identities of symmetry will be immediate consequences of this observation.
However, not all permutations of an expression in Section 3 yield distinct ones. In fact, as these expressions are obtained by permuting  ,
,  ,
,  in a single one labelled by them, they can be viewed as a group in a natural manner and hence it is isomorphic to a quotient of
in a single one labelled by them, they can be viewed as a group in a natural manner and hence it is isomorphic to a quotient of  . In particular, the numbers of possible distinct expressions are
. In particular, the numbers of possible distinct expressions are  ,
,  ,
,  or
or  . (a-0), (a-1(1)), (a-1(2)), and (a-2(2)) give the full six identities of symmetry, (a-2(1)) and (a-2(3)) yield three identities of symmetry, and (c-0) and (c-1) give two identities of symmetry, while the expression in (a-3) yields no identities of symmetry.
. (a-0), (a-1(1)), (a-1(2)), and (a-2(2)) give the full six identities of symmetry, (a-2(1)) and (a-2(3)) yield three identities of symmetry, and (c-0) and (c-1) give two identities of symmetry, while the expression in (a-3) yields no identities of symmetry.
Here we will just consider the cases of Theorems 4.8 and 4.17 leaving the others as easy exercises for the reader. As for the case of Theorem 4.8, in addition to (4.15)–(4.17), we get the following three ones:



But, by interchanging  and
and  , we see that (4.1), (4.2), and (4.3) are, respectively, equal to (4.15), (4.16), and (4.17).
, we see that (4.1), (4.2), and (4.3) are, respectively, equal to (4.15), (4.16), and (4.17).
As to Theorem  , in addition to (4.26) and (4.27), we have
, in addition to (4.26) and (4.27), we have




However, (4.4) and (4.5) are equal to (4.26), as we can see by applying the permutations  ,
,  , and
, and  for (4.4) and
for (4.4) and  ,
,  , and
, and  for (4.5). Similarly, we see that (4.6) and (4.7) are equal to (4.27), by applying permutations
for (4.5). Similarly, we see that (4.6) and (4.7) are equal to (4.27), by applying permutations  ,
,  , and
, and  for (4.6) and
for (4.6) and  ,
,  , and
, and  for (4.7).
for (4.7).
Theorem 4.1.
Let  ,
,  ,
,  be any positive integers. Then the following expression is invariant under any permutation of
be any positive integers. Then the following expression is invariant under any permutation of  ,
,  ,
,  , so that it gives us six symmetries:
, so that it gives us six symmetries:

Theorem 4.2.
Let  ,
,  ,
,  be any odd positive integers. Then the following expression is invariant under any permutation of
be any odd positive integers. Then the following expression is invariant under any permutation of  ,
,  ,
,  , so that it gives us six symmetries:
, so that it gives us six symmetries:

Putting  in (4.9), we get the following corollary.
in (4.9), we get the following corollary.
Corollary 4.3.
Let  ,
,  be any odd positive integers. Then one has
be any odd positive integers. Then one has

Letting further  in (4.10), we have the following corollary.
in (4.10), we have the following corollary.
Corollary 4.4.
Let  be any odd positive integer. Then one has
be any odd positive integer. Then one has

Theorem 4.5.
Let  be any odd positive integers. Then the following expression is invariant under any permutation of
be any odd positive integers. Then the following expression is invariant under any permutation of  ,
,  ,
,  , so that it gives us six symmetries:
, so that it gives us six symmetries:

Letting  in (4.12), we obtain alternative expressions for the identities in (4.10).
in (4.12), we obtain alternative expressions for the identities in (4.10).
Corollary 4.6.
Let  ,
,  be any odd positive integers. Then one has
be any odd positive integers. Then one has

Putting further  in (4.13), we have the alternative expressions for the identities for (4.11).
in (4.13), we have the alternative expressions for the identities for (4.11).
Corollary 4.7.
Let  be any odd positive integer. Then one has
be any odd positive integer. Then one has

Theorem 4.8.
Let  ,
,  ,
,  be any odd positive integers. Then one has the following three symmetries in
be any odd positive integers. Then one has the following three symmetries in  ,
,  ,
,  :
:



Putting  in (4.15)–(4.17), we get the following corollary.
in (4.15)–(4.17), we get the following corollary.
Corollary 4.9.
Let  ,
,  be any odd positive integers. Then one has
be any odd positive integers. Then one has

Letting further  in (4.18), we get the following corollary. This is also obtained in [20, Corollary
in (4.18), we get the following corollary. This is also obtained in [20, Corollary  ] and mentioned in [3].
] and mentioned in [3].
Corollary 4.10.
Let  be any odd positive integer. Then one has
be any odd positive integer. Then one has

Theorem 4.11.
Let  ,
,  ,
,  be any odd positive integers. Then the following expression is invariant under any permutation of
be any odd positive integers. Then the following expression is invariant under any permutation of  ,
,  ,
,  , so that it gives us six symmetries:
, so that it gives us six symmetries:

Putting  in (4.20), we obtain the following corollary. In Section 1, the identities in (4.18), (4.21), and (4.24) are combined to give those in (1.9)–(1.16).
in (4.20), we obtain the following corollary. In Section 1, the identities in (4.18), (4.21), and (4.24) are combined to give those in (1.9)–(1.16).
Corollary 4.12.
Let  ,
,  be any odd positive integers. Then one has
be any odd positive integers. Then one has

Letting further  in (4.21), we get the following corollary. This is the multiplication formula for Euler polynomials together with the relatively new identity mentioned in (4.19).
in (4.21), we get the following corollary. This is the multiplication formula for Euler polynomials together with the relatively new identity mentioned in (4.19).
Corollary 4.13.
Let  be any odd positive integer. Then one has
be any odd positive integer. Then one has

Theorem 4.14.
Let  ,
,  ,
,  be any odd positive integers. Then one has the following three symmetries in
be any odd positive integers. Then one has the following three symmetries in  ,
,  ,
,  :
:

Letting  in (4.23), we have the following corollary.
in (4.23), we have the following corollary.
Corollary 4.15.
Let  ,
,  be any odd positive integers. Then one has
be any odd positive integers. Then one has

Theorem 4.16.
Let  ,
,  ,
,  be any positive integers. Then one has the following two symmetries in
be any positive integers. Then one has the following two symmetries in  ,
,  ,
,  :
:

Theorem 4.17.
Let  ,
,  ,
,  be any odd positive integers. Then one has the following two symmetries in
be any odd positive integers. Then one has the following two symmetries in  ,
,  ,
,  :
:


Putting  in (4.26) and (4.27), we get the following corollary.
in (4.26) and (4.27), we get the following corollary.
Corollary 4.18.
Let  ,
,  be any odd positive integers. Then one has
be any odd positive integers. Then one has

References
Deeba EY, Rodriguez DM: Stirling's series and Bernoulli numbers. The American Mathematical Monthly 1991, 98(5):423–426. 10.2307/2323860
Howard FT: Applications of a recurrence for the Bernoulli numbers. Journal of Number Theory 1995, 52(1):157–172. 10.1006/jnth.1995.1062
Kim T: Symmetry -adic invariant integral on for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008, 14(12):1267–1277. 10.1080/10236190801943220
Kim T: Symmetry identities for the twisted generalized Euler polynomials. Advanced Studies in Contemporary Mathematics 2009, 19(2):151–155.
Kim T, Park KH, Hwang K-W: On the identities of symmetry for the -Euler polynomials of higher order. Advances in Difference Equations 2009, 2009:-9.
Kim T: Symmetry of power sum polynomials and multivariate fermionic -adic invariant integral on . Russian Journal of Mathematical Physics 2009, 16(1):93–96. 10.1134/S1061920809010063
Kim T: On the symmetries of the -Bernoulli polynomials. Abstract and Applied Analysis 2008, 2008:-7.
Kim T: -Volkenborn integration. Russian Journal of Mathematical Physics 2002, 9(3):288–299.
Kim T: Note on the Euler -zeta functions. Journal of Number Theory 2009, 129(7):1798–1804. 10.1016/j.jnt.2008.10.007
Kim T: On -adic interpolating function for -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008, 339(1):598–608. 10.1016/j.jmaa.2007.07.027
Kim T: On the -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007, 326(2):1458–1465. 10.1016/j.jmaa.2006.03.037
Kim T: On the analogs of Euler numbers and polynomials associated with -adic -integral on at . Journal of Mathematical Analysis and Applications 2007, 331(2):779–792. 10.1016/j.jmaa.2006.09.027
Kim T, Kim Y-H: On the symmetric properties for the generalized twisted Bernoulli polynomials. Journal of Inequalities and Applications 2009, 2009:-8.
Kim T, Jang L-C, Kim Y-H, Hwang K-W: On the identities of symmetry for the generalized Bernoulli polynomials attached to of higher order. Journal of Inequalities and Applications 2009, 2009:-7.
Ozden H, Cangul IN, Simsek Y: Multivariate interpolation functions of higher-order -Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.
Ozden H, Cangul IN, Simsek Y: Remarks on sum of products of -twisted Euler polynomials and numbers. Journal of Inequalities and Applications 2008, 2008:-8.
Ozden H, Simsek Y: A new extension of -Euler numbers and polynomials related to their interpolation functions. Applied Mathematics Letters 2008, 21(9):934–939. 10.1016/j.aml.2007.10.005
Simsek Y: Complete sum of products of -extension of Euler polynomials and numbers. Journal of Difference Equations and Applications 2009.
Tuenter HJH: A symmetry of power sum polynomials and Bernoulli numbers. The American Mathematical Monthly 2001, 108(3):258–261. 10.2307/2695389
Yang S-L: An identity of symmetry for the Bernoulli polynomials. Discrete Mathematics 2008, 308(4):550–554. 10.1016/j.disc.2007.03.030
Kim DS, Park KH: Identities of symmetry for Bernoulli polynomials arising from quotients of Volkenborn integrals invariant under S3, submitted
Acknowledgment
This work was supported by National Foundation of Korea Grant funded by the Korean Government (2009-0072514).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, D., Park, K. Identities of Symmetry for Euler Polynomials Arising from Quotients of Fermionic Integrals Invariant under  .
J Inequal Appl 2010, 851521 (2010). https://doi.org/10.1155/2010/851521
.
J Inequal Appl 2010, 851521 (2010). https://doi.org/10.1155/2010/851521
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/851521




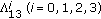 , we may consider the analogous things to the ones in (a-0), (a-1), (a-2), and (a-3). However, these do not lead us to new identities. Indeed, if we substitute
, we may consider the analogous things to the ones in (a-0), (a-1), (a-2), and (a-3). However, these do not lead us to new identities. Indeed, if we substitute 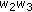 ,
, 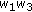 ,
, 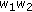 , respectively, for
, respectively, for  in (2.1), this amounts to replacing
in (2.1), this amounts to replacing 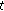 by
by  in (2.3). So, upon replacing
in (2.3). So, upon replacing 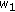 ,
, 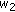 ,
, 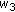 , respectively, by
, respectively, by 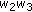 ,
, 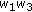 ,
, 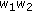 , and then dividing by
, and then dividing by 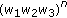 , in each of the expressions of Theorem 4.1 through Corollary 4.15, we will get the corresponding symmetric identities for Type
, in each of the expressions of Theorem 4.1 through Corollary 4.15, we will get the corresponding symmetric identities for Type 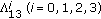 .
.