Abstract
We establish some maximal inequalities for demimartingales which generalize the result of Wang (2004). The maximal inequality for demimartingales is used as a key inequality to establish other results including Doob's type maximal inequality, strong law of large numbers, strong growth rate, and integrability of supremum for demimartingales, which generalize and improve partial results of Christofides (2000) and Prakasa Rao (2007).
Similar content being viewed by others
1. Introduction
Definition 1.1.
Let  be an
be an  sequence of random variables. Assume that for
sequence of random variables. Assume that for 

for all coordinatewise nondecreasing functions  such that the expectation is defined. Then
such that the expectation is defined. Then  is called a demimartingale. If in addition the function
is called a demimartingale. If in addition the function  is assumed to be nonnegative, then the sequence
is assumed to be nonnegative, then the sequence  is called a demisubmartingale.
is called a demisubmartingale.
Definition 1.2.
A finite collection of random variables  is said to be associated if
is said to be associated if

for any two coordinatewise nondecreasing functions  on
on  such that the covariance is defined. An infinite sequence
such that the covariance is defined. An infinite sequence  is associated if every finite subcollection is associated.
is associated if every finite subcollection is associated.
Definition 1.3.
A finite collection of random variables  is said to be strongly positive dependent if
is said to be strongly positive dependent if

for all Borel measurable and increasing (or decreasing) set pairs  (A set
(A set  is said increasing (or decreasing) if
is said increasing (or decreasing) if  implies
implies  for any
for any  ), where
), where

An infinite sequence  is strongly positive dependent if every finite subcollection is strongly positive dependent.
is strongly positive dependent if every finite subcollection is strongly positive dependent.
Remark 1.4.
Chow [1] proved a maximal inequality for submartingales. Newman and Wright [2] extended Doob's maximal inequality and upcrossing inequality to the case of demimartingales, and pointed out that the partial sum of a sequence of mean zero associated random variables is a demimartingale. Christofides [3] showed that the Chow's maximal inequality for (sub)martingales can be extended to the case of demi(sub)martingales. Wang [4] obtained Doob's type inequality for more general demimartingales. Hu et al. [5] gave a strong law of large numbers and growth rate for demimartingales. Prakasa Rao [6] established some maximal inequalities for demisubmartingales and N-demisuper-martingales.
It is easily seen that the partial sum of a sequence of mean zero strongly positive dependent random variables is also a demimartingale by the inequality (3) in Zheng [7], that is, for all  ,
,

for all coordinatewise nondecreasing functions  such that the expectation is defined. Therefore, the main results of this paper hold for the partial sums of sequences of mean zero associated random variables and strongly positive dependent random variables.
such that the expectation is defined. Therefore, the main results of this paper hold for the partial sums of sequences of mean zero associated random variables and strongly positive dependent random variables.
Let  and
and  be sequences of random variables defined on a fixed probability space
be sequences of random variables defined on a fixed probability space  and
and  the indicator function of the event
the indicator function of the event  . Denote
. Denote  ,
,  ,
,  ,
,  ,
,  . The main results of this paper depend on the following lemmas.
. The main results of this paper depend on the following lemmas.
Lemma 1.5 (see Wang [4, Theorem  ]).
]).
Let  be a demimartingale and
be a demimartingale and  a nonnegative convex function on
a nonnegative convex function on  with
with  and
and  . Let
. Let  be a nonincreasing sequence of positive numbers. Then for any
be a nonincreasing sequence of positive numbers. Then for any  ,
,

Lemma 1.6 (see Fazekas and Klesov [8, Theorem  ] and Hu et al. [5, Lemma
] and Hu et al. [5, Lemma  ]).
]).
Let  be a random variable sequence and
be a random variable sequence and  for
for  . Let
. Let  be a nondecreasing unbounded sequence of positive numbers and
be a nondecreasing unbounded sequence of positive numbers and  nonnegative numbers. Let
nonnegative numbers. Let  and
and  be fixed positive numbers. Assume that for each
be fixed positive numbers. Assume that for each  ,
,

then

and with the growth rate

where

In addition,

If further assumes one that  for infinitely many
for infinitely many  , then
, then

Lemma 1.7 (see Christofides [3, Lemma  , Corollary
, Corollary  ]).
]).
-
(i)
If
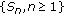 is a demisubmartingale (or a demimartingale) and
is a demisubmartingale (or a demimartingale) and 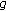 is a nondecreasing convex function such that
is a nondecreasing convex function such that 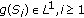 , then
, then  is a demisubmartingale.
is a demisubmartingale. -
(ii)
If
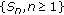 is a demimartingale, then
is a demimartingale, then 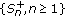 is a demisubmartingale and
is a demisubmartingale and 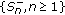 is a demisubmartingale.
is a demisubmartingale.
Lemma 1.8 (see Hu et al. [9, Theorem  ]).
]).
Let  be a demimartingale and
be a demimartingale and  be a nonincreasing sequence of positive numbers. Let
be a nonincreasing sequence of positive numbers. Let  and
and  for each
for each  , then for any
, then for any  and
and  ,
,

Lemma 1.9 (see Christofides [3, Corollary  , Theorem
, Theorem  ]).
]).
-
(i)
Let
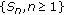 be a demisubmartingale. Then for any
be a demisubmartingale. Then for any 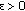 ,
,

-
(ii)
Let
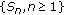 be a demisubmartingale and
be a demisubmartingale and 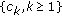 a nonincreasing sequence of positive numbers. Then for any
a nonincreasing sequence of positive numbers. Then for any 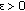 ,
,

Using Lemma 1.5, Wang [4] obtained the following inequalities for demimartingales.
Theorem 1.10 (see Wang [4, Corollary  ]).
]).
Let  be a demimartingale and
be a demimartingale and  a nonincreasing sequence of positive numbers. Then
a nonincreasing sequence of positive numbers. Then


We point out that there is a mistake in the proof of (1.17), that is,

should be replaced by

In fact, by Lemma 1.5 and Fubini Theorem, we can see that

The rest of the proof is similar to Corollary  in Wang [4].
in Wang [4].
The same problem exists in Shiryaev [10, page 495, in the proof of Theorem  ] and Krishna and Soumendra [11, page 414, in the proof of Theorem
] and Krishna and Soumendra [11, page 414, in the proof of Theorem  ]. For example, the following inequality
]. For example, the following inequality

in Shiryaev [10, page 495] should be revised as

2. Main Results and Their Proofs
Theorem 2.1.
Let  be a demimartingale and
be a demimartingale and  a nonnegative convex function on
a nonnegative convex function on  with
with  . Let
. Let  be a nonincreasing sequence of positive numbers.
be a nonincreasing sequence of positive numbers.  . Suppose that
. Suppose that  for each
for each  , then for every
, then for every  ,
,


Proof.
By Lemma 1.5 and Hölder's inequality, we have

where  is a real number and satisfies
is a real number and satisfies  Since
Since  for each
for each  , we can obtain
, we can obtain

therefore,

Similar to the proof of (2.3) and using Lemma 1.5 again, we can see that

For constants  and
and  , it follows that
, it follows that

Combining (2.6) and (2.7), we have

Thus, (2.2) follows from (2.8) immediately. The proof is complete.
Remark 2.2.
If we take  in Theorem 2.1, then Theorem 2.1 implies Corollary 2.1 in Wang [4].
in Theorem 2.1, then Theorem 2.1 implies Corollary 2.1 in Wang [4].
Corollary 2.3.
Let the conditions of Theorem 2.1 be satisfied with  for each
for each  . Then for every
. Then for every  ,
,


Corollary 2.4 (Doob's type maximal inequality for demimartingales).
Let  and
and  be a demimartingale. Suppose that
be a demimartingale. Suppose that  for each
for each  , then for every
, then for every  ,
,

Theorem 2.5.
Let  be a demimartingale and
be a demimartingale and  a nonnegative convex function on
a nonnegative convex function on  with
with  . Let
. Let  be a nondecreasing unbounded sequence of positive numbers.
be a nondecreasing unbounded sequence of positive numbers.  . Suppose that
. Suppose that  for each
for each  and
and

then  , and (1.9)-(1.10) hold (
, and (1.9)-(1.10) hold ( is replaced by
is replaced by  ), where
), where

In addition,

If further one assumes that  for infinitely many
for infinitely many  , then
, then

Proof.
By the condition of the theorem, we can see that  for all
for all  . Thus,
. Thus,

follows from (2.9) for each  . By (2.12), we have
. By (2.12), we have

Therefore,  follows from Lemma 1.6, (2.16), and (2.17); (1.9), (1.10), (2.14), (2.15) hold. This completes the proof of the theorem.
follows from Lemma 1.6, (2.16), and (2.17); (1.9), (1.10), (2.14), (2.15) hold. This completes the proof of the theorem.
In Theorem 2.5, if we assume that  is a nonnegative and nondecreasing convex function on
is a nonnegative and nondecreasing convex function on  with
with  , then the condition "
, then the condition " for each
for each  " is satisfied.
" is satisfied.
Remark 2.6.
Theorem 2.5 generalizes and improves the results of Theorem  in Christofides [3] and Theorem
in Christofides [3] and Theorem  in Prakasa Rao [6].
in Prakasa Rao [6].
Theorem 2.7.
Let  and
and  a demimartingale with
a demimartingale with  for each
for each  . Let
. Let  be a nondecreasing sequence of positive numbers. If
be a nondecreasing sequence of positive numbers. If

then for any  ,
,

Proof.
Taking  ,
,  and
and  in Lemma 1.8, we have
in Lemma 1.8, we have

Thus, by (2.20) and (2.18), we can get

Theorem 2.8.
Let  be a demisubmartingale and
be a demisubmartingale and  a nondecreasing and nonnegative convex function on
a nondecreasing and nonnegative convex function on  with
with  and
and  . Let
. Let  be a nonincreasing sequence of positive numbers. Then for all
be a nonincreasing sequence of positive numbers. Then for all  and each
and each  ,
,

Proof.
By Fubini theorem, it is easy to check that

It follows from Lemma 1.7(i) and Lemma 1.9(ii) that

Therefore, (2.22) follows from the above statements immediately.
Corollary 2.9.
Let the conditions of Theorem 2.8 be satisfied with  for each
for each  . Then for all
. Then for all  and each
and each  ,
,

By Corollary 2.9, we can get the following theorem.
Theorem 2.10.
Let  be a demisubmartingale and
be a demisubmartingale and  a nondecreasing and nonnegative convex function on
a nondecreasing and nonnegative convex function on  with
with  and
and  . Let
. Let  be a nondecreasing unbounded sequence of positive numbers. If there exists some
be a nondecreasing unbounded sequence of positive numbers. If there exists some  such that
such that

then  a.s., and (1.9)-(1.10) hold (
a.s., and (1.9)-(1.10) hold ( is replaced by
is replaced by  ), where
), where

In addition,

If further one assumes that  for infinitely many
for infinitely many  , then
, then

Similar to the proof of Theorem 2.8 and using Lemma 1.9(i), we can get the following.
Theorem 2.11.
Let  be a nonnegative demisubmartingale. Then for all
be a nonnegative demisubmartingale. Then for all  ,
,  .
.
References
Chow YS: A martingale inequality and the law of large numbers. Proceedings of the American Mathematical Society 1960, 11: 107–111. 10.1090/S0002-9939-1960-0112190-3
Newman CM, Wright AL: Associated random variables and martingale inequalities. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1982, 59(3):361–371. 10.1007/BF00532227
Christofides TC: Maximal inequalities for demimartingales and a strong law of large numbers. Statistics & Probability Letters 2000, 50(4):357–363. 10.1016/S0167-7152(00)00116-4
Wang JF: Maximal inequalities for associated random variables and demimartingales. Statistics & Probability Letters 2004, 66(3):347–354. 10.1016/j.spl.2003.10.021
Hu SH, Chen GJ, Wang XJ: On extending the Brunk-Prokhorov strong law of large numbers for martingale differences. Statistics & Probability Letters 2008, 78(18):3187–3194. 10.1016/j.spl.2008.06.017
Prakasa Rao BLS: On some maximal inequalities for demisubmartingales and -demisuper martingales. Journal of Inequalities in Pure and Applied Mathematics 2007, 8(4, article 112):1–17.
Zheng YH: Inequalities of moment and convergence theorem of order statistics of partial sums for a class of strongly positive dependent stochastic sequence. Acta Mathematicae Applicatae Sinica 2001, 24(2):168–176.
Fazekas I, Klesov O: A general approach rate to the strong law of large numbers. Statistics & Probability Letters 2001, 45(3):436–449.
Hu SH, Wang XJ, Yang WZ, Zhao T: The Hàjek-Rènyi-type inequality for associated random variables. Statistics & Probability Letters 2009, 79(7):884–888. 10.1016/j.spl.2008.11.014
Shiryaev AN: Probability, Graduate Texts in Mathematics. Volume 95. 2nd edition. Springer, New York, NY, USA; 1996:xvi+623.
Athreya KB, Lahiri SN: Measure Theory and Probability Theory, Springer Texts in Statistics. Springer, New York, NY, USA; 2006:xviii+618.
Acknowledgments
The authors are most grateful to the Editor Andrei Volodin and an anonymous referee for the careful reading of the manuscript and valuable suggestions which helped in significantly improving an earlier version of this paper. This work was supported by the National Natural Science Foundation of China (Grant no. 10871001, 60803059), Talents Youth Fund of Anhui Province Universities (Grant no. 2010SQRL016ZD), Youth Science Research Fund of Anhui University (Grant no. 2009QN011A), Provincial Natural Science Research Project of Anhui Colleges and the Innovation Group Foundation of Anhui University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xuejun, W., Shuhe, H., Ting, Z. et al. Doob's Type Inequality and Strong Law of Large Numbers for Demimartingales. J Inequal Appl 2010, 838301 (2010). https://doi.org/10.1155/2010/838301
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/838301



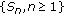 is a demisubmartingale (or a demimartingale) and
is a demisubmartingale (or a demimartingale) and 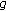 is a nondecreasing convex function such that
is a nondecreasing convex function such that 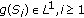 , then
, then  is a demisubmartingale.
is a demisubmartingale.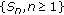 is a demimartingale, then
is a demimartingale, then 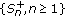 is a demisubmartingale and
is a demisubmartingale and 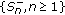 is a demisubmartingale.
is a demisubmartingale.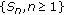 be a demisubmartingale. Then for any
be a demisubmartingale. Then for any 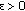 ,
,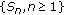 be a demisubmartingale and
be a demisubmartingale and 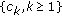 a nonincreasing sequence of positive numbers. Then for any
a nonincreasing sequence of positive numbers. Then for any 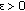 ,
,