Abstract
The nonlocal boundary value problem, with  -Laplacian of the form
-Laplacian of the form 
 , has been considered. Two existence criteria of at least one and three positive solutions are presented. The first one is based on the Four functionals fixed point theorem in the work of R. Avery et al. (2008), and the second one is based on the Five functionals fixed point theorem. Meanwhile an example is worked out to illustrate the main result.
, has been considered. Two existence criteria of at least one and three positive solutions are presented. The first one is based on the Four functionals fixed point theorem in the work of R. Avery et al. (2008), and the second one is based on the Five functionals fixed point theorem. Meanwhile an example is worked out to illustrate the main result.
Similar content being viewed by others
1. Introduction
Due to the unification of the theory of differential and difference equations, there have been many investigations working on the existence of positive solutions to boundary value problems for dynamic equations on time scales. Also there is much attention paid to the study of multipoint boundary value problem with  -Laplacian; see [1–10].
-Laplacian; see [1–10].
For convenience, throughout this paper we denote  as the
as the  -Laplacian operator, that is,
-Laplacian operator, that is,  ,
,  .
.  , where
, where  .
.
In [11], the author discussed the positive solutions of a  -point boundary value problem for a second-order dynamic equation on a time scale
-point boundary value problem for a second-order dynamic equation on a time scale

where  ,
, 
 , and
, and  with
with  . And he got the existence of at least two positive solutions of the above problem by means of a fixed point theorem in a cone.
. And he got the existence of at least two positive solutions of the above problem by means of a fixed point theorem in a cone.
Zhao and Ge [9] considered the following multi-point boundary value problem with one-dimensional  -Laplacian:
-Laplacian:

where  ,
,  ,
,  ,
,  ,
,  ,
,  . By using a fixed point theorem in a cone, they obtained the existence of at least one, two, or three positive solutions under some sufficient conditions.
. By using a fixed point theorem in a cone, they obtained the existence of at least one, two, or three positive solutions under some sufficient conditions.
Motivated by the above results, in this paper, we investigate the nonlocal boundary value problem with  -Laplacian
-Laplacian

where  and
and  .
.
For convenience, we list the following hypotheses:
-
(H1)
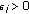 ,
,  ,
, 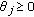 ,
,  ,
,  ;
; -
(H2)
 and
and 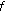 is not identically zero on any compact subinterval of
is not identically zero on any compact subinterval of 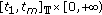 ;
; -
(H3)
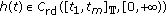 and
and  is not identically zero on any compact subinterval of
is not identically zero on any compact subinterval of  , also it satisfies
, also it satisfies (1.4)
(1.4)
By using the Four functionals fixed point theorem and Five functionals fixed point theorem, we obtain the existence criteria of at least one positive solution and three positive solutions for the BVP (1.3). As an application, an example is worked out finally. The remainder of this paper is organized as follows. Section 2 is devoted to some preliminary discussions. We give and prove our main results in Section 3.
2. Preliminaries
The basic definitions and notations on time scales can be found in [12, 13]. In the following, we will provide some background materials on the theory of cones in Banach spaces. For more details, please refer to [14, 15].
Definition 2.1.
Let  be a Banach space. A nonempty, closed set
be a Banach space. A nonempty, closed set  is said to be a cone provided that the following hypotheses are satisfied:
is said to be a cone provided that the following hypotheses are satisfied:
-
(1)
if
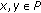 ,
,  , then
, then 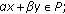
-
(2)
if
 ,
,  , then
, then 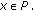
Every cone  induces a partial ordering "
induces a partial ordering " " on
" on  defined by
defined by  if and only if
if and only if 
Definition 2.2.
A map  is said to be a nonnegative continuous concave functional on a cone
is said to be a nonnegative continuous concave functional on a cone  of a real Banach space
of a real Banach space  if
if  is continuous and
is continuous and  for all
for all 
 and
and  . Similarly, we say that the map
. Similarly, we say that the map  is a nonnegative continuous convex functional on a cone
is a nonnegative continuous convex functional on a cone  of a real Banach space
of a real Banach space  if
if  is continuous and
is continuous and  for all
for all 
 and
and  .
.
Let  and
and  be nonnegative continuous concave functionals on
be nonnegative continuous concave functionals on  , and let
, and let  and
and  be nonnegative continuous convex functionals on
be nonnegative continuous convex functionals on  ; then for positive numbers
; then for positive numbers  and
and  , define the sets
, define the sets

The following lemma can be found in [16].
Lemma 2.3 (four functionals fixed point theorem).
If P is a cone in a real Banach space E,  and
and  are nonnegative continuous concave functionals on
are nonnegative continuous concave functionals on  ,
,  and
and  are nonnegative continuous convex functionals on
are nonnegative continuous convex functionals on  , and there exist nonnegative positive numbers
, and there exist nonnegative positive numbers  and
and  , such that
, such that

is a completely continuous operator, and  is a bounded set. If
is a bounded set. If
-
(i)

-
(ii)
 , for all
, for all 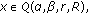 with
with 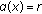 and
and 
-
(iii)
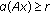 , for all
, for all  with
with 
-
(iv)
 , for all
, for all 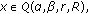 with
with  and
and  ,
, -
(v)
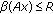 , for all
, for all  with
with 
then  has a fixed point
has a fixed point  in
in  .
.
We are now in a position to present the Five functionals fixed point theorem (see [17]). Let  be nonnegative continuous convex functionals on
be nonnegative continuous convex functionals on  and
and  nonnegative continuous concave functionals on
nonnegative continuous concave functionals on  . For nonnegative numbers
. For nonnegative numbers  and
and  define the following convex sets:
define the following convex sets:

Lemma 2.4 (five functionals fixed point theorem).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . Suppose that there exist nonnegative numbers
. Suppose that there exist nonnegative numbers  and
and  , nonnegative continuous concave functionals
, nonnegative continuous concave functionals  and
and  on
on  , and nonnegative continuous convex functionals
, and nonnegative continuous convex functionals  and
and  on
on  , with
, with

Suppose that  is completely continuous and there exist nonnegative numbers
is completely continuous and there exist nonnegative numbers  with
with  such that
such that
-
(i)
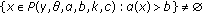 and
and 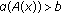 for
for 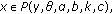
-
(ii)
 and
and  for
for 
-
(iii)
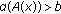 for
for  with
with 
-
(iv)
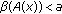 for
for 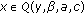 with
with 
then A has at least three fixed points  such that
such that

Consider the Banach space  equipped with the norm
equipped with the norm  . Suppose
. Suppose  ,
,  with
with  . For the sake of convenience, we take the notations
. For the sake of convenience, we take the notations

Define a cone

and an operator  by
by

Lemma 2.5.
 .
.
Proof.
For  ,
,  ,
,

From the definition of  , it is clear that
, it is clear that

is continuous,  and
and  is the maximum value of
is the maximum value of  on
on  .
.
Let  , then
, then  is continuous,
is continuous,  is delta differentiable on
is delta differentiable on  , and
, and  is continuously differentiable. Moreover
is continuously differentiable. Moreover  is monotonically increasing for
is monotonically increasing for  and
and  . Then by the chain rule [12, Theorem
. Then by the chain rule [12, Theorem  , page 31], we obtain
, page 31], we obtain

where  is in the interval
is in the interval  . So,
. So,  . This completes the proof.
. This completes the proof.
3. Main Results and an Example
Theorem 3.1.
Assume that (H1), (H2), and (H3) hold, if there exist constants  ,
,  ,
,  ,
,  with
with  ,
,  ,
,  and suppose that
and suppose that  satisfies the following conditions:
satisfies the following conditions:
(A1) for all
for all 
(A2) for all
for all 
then the BVP (1.3) has a fixed point  such that
such that

Define maps

and let  ,
,  and
and  be defined by (2.1).
be defined by (2.1).
In order to complete the proof of Theorem 3.1, we first need to prove the following lemma.
Lemma 3.2.
 is bounded and
is bounded and  is completely continuous.
is completely continuous.
Proof.
For all  ,
,  , which means that
, which means that  is a bounded set.
is a bounded set.
According to Lemma 2.5, it is clear that  .
.
In view of the continuity of  , there exists a constant
, there exists a constant  such that
such that  , for all
, for all  ,
,  . Consider
. Consider

which means that  is uniformly bounded.
is uniformly bounded.
In addition, for all  , we have
, we have

Applying the Arzelà-Ascoli theorem on time scales [18], one can show that  is relatively compact.
is relatively compact.
Now we prove that  is continuous. Let
is continuous. Let  be a sequence in
be a sequence in  which converges to
which converges to  uniformly on
uniformly on  . Because
. Because  is relatively compact, the sequence
is relatively compact, the sequence  admits a subsequence
admits a subsequence  converging to
converging to  uniformly on
uniformly on  . In addition,
. In addition,

Observe that

Hence, by the Lebesgue's dominated convergence theorem on time scales [19], insert  into the above equality and then let
into the above equality and then let  , we obtain
, we obtain

From the definition of  , we know that
, we know that  on
on  . This shows that each subsequence of
. This shows that each subsequence of  uniformly converges to
uniformly converges to  . Therefore the sequence
. Therefore the sequence  uniformly converges to
uniformly converges to  . This means that
. This means that  is continuous at
is continuous at  . So,
. So,  is continuous on
is continuous on  since
since  is arbitrary. Thus,
is arbitrary. Thus,  is completely continuous. This completes the proof.
is completely continuous. This completes the proof.
Proof of Theorem 3.1.
Let

Clearly,  . By direct calculation,
. By direct calculation,

So,  which means that (i) in Lemma 2.3 is satisfied.
which means that (i) in Lemma 2.3 is satisfied.
For all  with
with  and
and  , we have
, we have  , and for all
, and for all  with
with  and
and  , we obtain that
, we obtain that  . Hence, (ii) and (iv) in Lemma 2.3 are fulfilled.
. Hence, (ii) and (iv) in Lemma 2.3 are fulfilled.
For any  with
with 

and for all  with
with  ,
,

Thus (iii) and (v) in Lemma 2.3 hold true. So, by Lemma 2.3, the BVP (1.3) has a fixed point  in
in  . This completes the proof.
. This completes the proof.
Theorem 3.3.
Assume that (H1), (H2), and (H3) hold. If there exist constants  , with
, with  ,
,  ,
,  ,
,  ,
,  , further suppose that
, further suppose that  satisfies the following conditions:
satisfies the following conditions:
(B1) for all
for all 
(B2) for all
for all 
then the BVP (1.3) has at least three positive solutions  ,
,  and
and  such that
such that

Proof.
Define these maps

and let 
 ,
,  ,
,  and
and  be defined by (2.3). It is clear that
be defined by (2.3). It is clear that

Using similar methods as those in Lemma 3.2, we obtain that  is completely continuous. Thus, we only need to show that
is completely continuous. Thus, we only need to show that  . Let
. Let  , then
, then

which implies that  .
.
Let  and
and

we can verify that  . By calculation,
. By calculation,

So,  ,
,  ,
,  ,
,  which means that
which means that  and
and  are not empty.
are not empty.
For  ,
,

and for  ,
,

Thus (i) and (ii) in Lemma 2.4 hold.
On the other hand, for  with
with  , we have
, we have  . And for
. And for  with
with  , we can obtain
, we can obtain  Thus, (iii) and (iv) in Lemma 2.4 hold.
Thus, (iii) and (iv) in Lemma 2.4 hold.
So, by Lemma 2.4, we obtain that the BVP (1.3) has at least three positive solutions  such that
such that

This completes the proof.
Remark 3.4.
Let  ,
,  ,
,  , we can find that the conditions of Theorem 3.1 are contained in Theorem 3.3.
, we can find that the conditions of Theorem 3.1 are contained in Theorem 3.3.
Example 3.5.
Let  ,
,  , consider the following eight-point BVP:
, consider the following eight-point BVP:

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , for all
, for all  , and
, and

where  is continuous,
is continuous,  , and
, and  .
.
Set  ,
,  , by calculation,
, by calculation,

and let  ,
,  ,
,  ,
,  ,
,  . Clearly, we can verify that the conditions in Theorem 3.3 are fulfilled. Thus, by Theorem 3.3, the BVP (3.21) has at least three positive solutions
. Clearly, we can verify that the conditions in Theorem 3.3 are fulfilled. Thus, by Theorem 3.3, the BVP (3.21) has at least three positive solutions  ,
,  and
and  such that
such that

Remark 3.6.
If we let  ,
,  ,
,  ,
,  , we can also verify that the conditions in Theorem 3.1 are satisfied.
, we can also verify that the conditions in Theorem 3.1 are satisfied.
References
Anderson D, Avery R, Henderson J:Existence of solutions for a one dimensional
 -Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416
-Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416Feng M, Feng H, Zhang X, Ge W:Triple positive solutions for a class of
 -point dynamic equations on time scales with
-point dynamic equations on time scales with  -Laplacian. Mathematical and Computer Modelling 2008,48(7-8):1213-1226. 10.1016/j.mcm.2007.12.016
-Laplacian. Mathematical and Computer Modelling 2008,48(7-8):1213-1226. 10.1016/j.mcm.2007.12.016Sang Y, Su H:Several existence theorems of nonlinear
 -point boundary value problem for
-point boundary value problem for  -Laplacian dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,340(2):1012-1026. 10.1016/j.jmaa.2007.09.029
-Laplacian dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,340(2):1012-1026. 10.1016/j.jmaa.2007.09.029Song C, Weng P:Multiple positive solutions for
 -Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043
-Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043Cao F, Han Z, Sun S:Existence of periodic solutions for
 -Laplacian equations on time scales. Advances in Difference Equations 2010,2010(1):-13.
-Laplacian equations on time scales. Advances in Difference Equations 2010,2010(1):-13.Sun H-R, Li W-T:Multiple positive solutions for
 -Laplacian
-Laplacian  -point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009
-point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009Sun H-R, Li W-T:Existence theory for positive solutions to one-dimensional
 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004Yang J, Wei Z:Existence of positive solutions for fourth-order
 -point boundary value problems with a one-dimensional
-point boundary value problems with a one-dimensional  -Laplacian operator. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7-8):2985-2996. 10.1016/j.na.2009.01.191
-Laplacian operator. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7-8):2985-2996. 10.1016/j.na.2009.01.191Zhao J, Ge W:Existence results of
 -point boundary value problem of Sturm-Liouville type with sign changing nonlinearity. Mathematical and Computer Modelling 2009,49(5-6):946-954. 10.1016/j.mcm.2008.08.022
-point boundary value problem of Sturm-Liouville type with sign changing nonlinearity. Mathematical and Computer Modelling 2009,49(5-6):946-954. 10.1016/j.mcm.2008.08.022Zhu Y, Zhu J:The multiple positive solutions for
 -Laplacian multipoint BVP with sign changing nonlinearity on time scales. Journal of Mathematical Analysis and Applications 2008,344(2):616-626. 10.1016/j.jmaa.2008.02.032
-Laplacian multipoint BVP with sign changing nonlinearity on time scales. Journal of Mathematical Analysis and Applications 2008,344(2):616-626. 10.1016/j.jmaa.2008.02.032He Z:Existence of two solutions of
 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Lakshmikantham V, Sivasundaram S, Kaymakcalan B: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Agarwal RP, O'Regan D: A generalization of the Petryshyn-Leggett-Williams fixed point theorem with applications to integral inclusions. Applied Mathematics and Computation 2001,123(2):263-274. 10.1016/S0096-3003(00)00077-1
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Avery R, Henderson J, O'Regan D: Four functionals fixed point theorem. Mathematical and Computer Modelling 2008,48(7-8):1081-1089. 10.1016/j.mcm.2007.12.013
Avery RI: A generalization of the Leggett-Williams fixed point theorem. Mathematical Sciences Research Hot-Line 1999,3(7):9-14.
Agarwal RP, Bohner M, Řehák P: Half-linear dynamic equations. In Nonlinear Analysis and Applications: to V. Lakshmikantham on His 80th Birthday. Vol. 1. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:1-57.
Aulbach B, Neidhart L: Integration on measure chains. In Proceedings of the 6th International Conference on Difference Equations, Boca Raton, Fla, USA. CRC; 2004:239-252.
Acknowledgments
This work is supported by the Natural Science Foundation of Ludong University (24200301, 24070301, 24070302), Program for Innovative Research Team in Ludong University, and a Project of Shandong Province Higher Educational Science and Technology Program.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, TT., Wang, LL. & Fan, YH. Existence of Positive Solutions to a Nonlocal Boundary Value Problem with  -Laplacian onTime Scales.
Adv Differ Equ 2010, 809497 (2010). https://doi.org/10.1155/2010/809497
-Laplacian onTime Scales.
Adv Differ Equ 2010, 809497 (2010). https://doi.org/10.1155/2010/809497
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/809497



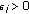 ,
,  ,
, 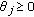 ,
,  ,
,  ;
; and
and 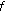 is not identically zero on any compact subinterval of
is not identically zero on any compact subinterval of 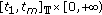 ;
;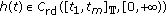 and
and  is not identically zero on any compact subinterval of
is not identically zero on any compact subinterval of  , also it satisfies
, also it satisfies
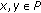 ,
,  , then
, then 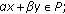
 ,
,  , then
, then 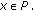

 , for all
, for all 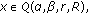 with
with 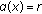 and
and 
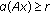 , for all
, for all  with
with 
 , for all
, for all 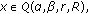 with
with  and
and  ,
,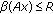 , for all
, for all  with
with 
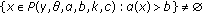 and
and 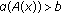 for
for 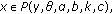
 and
and  for
for 
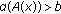 for
for  with
with 
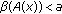 for
for 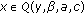 with
with 
 -Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416
-Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416 -point dynamic equations on time scales with
-point dynamic equations on time scales with  -Laplacian. Mathematical and Computer Modelling 2008,48(7-8):1213-1226. 10.1016/j.mcm.2007.12.016
-Laplacian. Mathematical and Computer Modelling 2008,48(7-8):1213-1226. 10.1016/j.mcm.2007.12.016 -point boundary value problem for
-point boundary value problem for  -Laplacian dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,340(2):1012-1026. 10.1016/j.jmaa.2007.09.029
-Laplacian dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,340(2):1012-1026. 10.1016/j.jmaa.2007.09.029 -Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043
-Laplacian functional dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):208-215. 10.1016/j.na.2006.10.043 -Laplacian equations on time scales. Advances in Difference Equations 2010,2010(1):-13.
-Laplacian equations on time scales. Advances in Difference Equations 2010,2010(1):-13. -Laplacian
-Laplacian  -point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009
-point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004 -point boundary value problems with a one-dimensional
-point boundary value problems with a one-dimensional  -Laplacian operator. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7-8):2985-2996. 10.1016/j.na.2009.01.191
-Laplacian operator. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7-8):2985-2996. 10.1016/j.na.2009.01.191 -point boundary value problem of Sturm-Liouville type with sign changing nonlinearity. Mathematical and Computer Modelling 2009,49(5-6):946-954. 10.1016/j.mcm.2008.08.022
-point boundary value problem of Sturm-Liouville type with sign changing nonlinearity. Mathematical and Computer Modelling 2009,49(5-6):946-954. 10.1016/j.mcm.2008.08.022 -Laplacian multipoint BVP with sign changing nonlinearity on time scales. Journal of Mathematical Analysis and Applications 2008,344(2):616-626. 10.1016/j.jmaa.2008.02.032
-Laplacian multipoint BVP with sign changing nonlinearity on time scales. Journal of Mathematical Analysis and Applications 2008,344(2):616-626. 10.1016/j.jmaa.2008.02.032 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051