Abstract
We consider the propagator of an evolution equation, which is a semigroup of linear operators. Questions related to its operator norm function and its behavior at the critical point for norm continuity or compactness or differentiability are studied.
Similar content being viewed by others
1. Introduction
As it is well known, each well-posed Cauchy problem for first-order evolution equation in Banach spaces

gives rise to a well-defined propagator, which is a semigroup of linear operators, and the theory of semigroups of linear operators on Banach spaces has developed quite rapidly since the discovery of the generation theorem by Hille and Yosida in 1948. By now, it is a rich theory with substantial applications to many fields (cf., e.g., [1–6]).
In this paper, we pay attention to some basic problems on the semigroups of linear operators and reveal some essential properties of theirs.
Let  be a Banach space.
be a Banach space.
A one-parameter family
 of bounded linear operators on
of bounded linear operators on
 is called a strongly continuous semigroup (or simply
is called a strongly continuous semigroup (or simply
 -semigroup) if it satisfies the following conditions:
-semigroup) if it satisfies the following conditions:
-
(i)
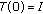 , with (
, with (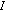 being the identity operator on X) ,
being the identity operator on X) , -
(ii)
 for
for 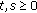 ,
, -
(iii)
the map
 is continuous on
is continuous on 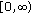 for every
for every 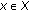 .
.
The infinitesimal generator of
of  is defined as
is defined as

with domain

For a comprehensive theory of  -semigroups we refer to [2].
-semigroups we refer to [2].
2. Properties of the Function 
Let  be a
be a  -semigroup on
-semigroup on  and define
and define  for
for  . Clearly, from Definition 1.1 we see that
. Clearly, from Definition 1.1 we see that
-
(I)
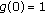 ,
, 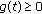 for
for 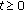 ;
; -
(II)
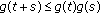 for
for  .
.
Furthermore, we can infer from the strong continuity of  that
that

-
(III)
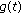 is lower-semicontinuous, that is,
is lower-semicontinuous, that is, (2.1)
(2.1)In fact,
 (2.2)
(2.2)holds for all
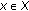 with
with 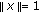 . Thus, taking the supremum for all
. Thus, taking the supremum for all 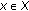 with
with 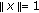 on the left-hand side leads to (2.1).
on the left-hand side leads to (2.1).
We ask the following question
For every function satisfying
satisfying ,
, , and
, and , does there exist a
, does there exist a semigroup
semigroup on some Banach space
on some Banach space such that
such that for all
for all ?
?
We show that this is not true even if  is a finite-dimensional space.
is a finite-dimensional space.
Theorem 2.1.
Let  be an
be an  -dimensional Banach space with
-dimensional Banach space with  . Let
. Let

Then  satisfies (I), (II), and (III), and there exists no
satisfies (I), (II), and (III), and there exists no  semigroup
semigroup  on
on  such that
such that  for all
for all  .
.
Proof.
First, we show that  satisfies (I), (II), and (III). (I) is clearly satisfied.
satisfies (I), (II), and (III). (I) is clearly satisfied.
To show (III) and (II), we write

Then

hence  satisfies (III).
satisfies (III).
For (II), suppose  , and consider the following four cases.
, and consider the following four cases.
Case 1 ( and
and  ).
).
In this case

that is,

Case 2 ( and
and  ).
).
Let

Then

and  is a convex function on
is a convex function on  . So by Jensen's inequality, we have
. So by Jensen's inequality, we have

that is,

Therefore

that is,  .
.
Case 3 ( , but
, but  and
and  ).
).
It follows from Case 2 that

Case 4 ( ).
).
Again we have

Next, we prove that there does not exist any  semigroup
semigroup  on
on  such that
such that  . Suppose
. Suppose  for some
for some  semigroup
semigroup  on
on  and let
and let  be its infinitesimal generator.
be its infinitesimal generator.
First we note from (2.3) that

for every  , while
, while

By the well-known Lyapunov theorem [2, Chapter I, Theorem  ], all eigenvalues of
], all eigenvalues of  (the infinitesimal generator of
(the infinitesimal generator of  ) have negative parts for every
) have negative parts for every  . Letting
. Letting  be the eigenvalues of
be the eigenvalues of  , we then have
, we then have

and this implies that

It is known that there is an isomorphism  of
of  onto
onto  such that
such that

where  is the Jordan block corresponding to
is the Jordan block corresponding to  . Therefore
. Therefore

Set

where  is the order of
is the order of  . Then
. Then  is a
is a  th nilpotent matrix with
th nilpotent matrix with  for each
for each  . According to (2.20) and (2.18), we have
. According to (2.20) and (2.18), we have

Observing

we see that

Thus,

which is a contradiction to (2.16).
Open Problem 1.
Is it possible that there exists an  with
with  and a
and a  semigroup
semigroup  on
on  such that
such that  for all
for all  ?
?
3. The Critical Point of Norm-Continuous (Compact, Differentiable) Semigroups
The following definitions are basic [1–6].
Definition 3.1.
A
 -semigroup
-semigroup
 is called norm-continuous for
is called norm-continuous for
 if
if
 is continuous in the uniform operator topology for
is continuous in the uniform operator topology for
 .
.
Definition 3.2.
A
 -semigroup
-semigroup
 is called compact for
is called compact for
 if
if
 is a compact operator for
is a compact operator for
 .
.
Definition 3.3.
A
 -semigroup
-semigroup
 is called differentiable for
is called differentiable for
 if for every
if for every
 ,
,
 is differentiable for
is differentiable for
 .
.
It is known that if a  -semigroup
-semigroup  is norm continuous (compact, differentiable) at
is norm continuous (compact, differentiable) at  , then it remains so for all
, then it remains so for all  . For instance, the following holds.
. For instance, the following holds.
Proposition 3.4.
If the map  is right differentiable at
is right differentiable at  , then it is also differentiable for
, then it is also differentiable for  .
.
Therefore, if we write

and suppose  (
( ,
,  ), then
), then  (
( ,
,  ) takes the form of
) takes the form of  for a nonnegative real number
for a nonnegative real number  . In other words, if
. In other words, if  (
( ,
,  ), then
), then  is norm continuous (compact, differentiable) on the interval
is norm continuous (compact, differentiable) on the interval  but not at any point in
but not at any point in  . We call
. We call  the critical point of the norm continuity (compactness, differentiability) of operator semigroup
the critical point of the norm continuity (compactness, differentiability) of operator semigroup  .
.
A natural question is the following
Suppose that is the critical point of the norm continuity
is the critical point of the norm continuity compactness, differentiability
compactness, differentiability of the operator semigroup
of the operator semigroup . Is
. Is also norm continuous (compact, differentiable) at
also norm continuous (compact, differentiable) at ? Of course, concerning norm continuity or differentiability at
? Of course, concerning norm continuity or differentiability at  we only mean right continuity or right differentiability.
we only mean right continuity or right differentiability.
We show that the answer is "yes" in some cases and "no" for other cases.
Example 3.5.
Let
 and
and

Then clearly  for
for  . Moreover,
. Moreover,  is not norm continuous (not compact, not differentiable) for any
is not norm continuous (not compact, not differentiable) for any  since
since

for sufficiently small  , where
, where

Therefore, in this case we have  . Since
. Since  , we see that
, we see that  is compact and
is compact and  is differentiable at
is differentiable at  from the right.
from the right.
Example 3.6.
Let

with supremum norm. For any  set
set

Then,  is compact (hence norm-continuous) for
is compact (hence norm-continuous) for  since
since  is the operator-norm limit of a sequence
is the operator-norm limit of a sequence  of finite-rank operators:
of finite-rank operators:

where

So the critical point for compactness and norm continuity is  . However, the infinitesimal generator of
. However, the infinitesimal generator of  is given by
is given by

with

In view of that  is unbounded, we know that
is unbounded, we know that  is not norm continuous at
is not norm continuous at  .
.
For differentiability, we note that  is differentiable at
is differentiable at  if and only if
if and only if  for each
for each  . From
. From

it follows that when  ,
,  for every
for every  . On the other hand, when
. On the other hand, when  and
and  is any nonzero constant sequence,
is any nonzero constant sequence,  . Therefore the critical point for differentiability is
. Therefore the critical point for differentiability is  . But
. But  is not differentiable at
is not differentiable at  .
.
References
Davies EB: One-Parameter Semigroups, London Mathematical Society Monographs. Volume 15. Academic Press, London, UK; 1980:viii+230.
Engel K-J, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000:xxii+586.
Fattorini HO: The Cauchy Problem, Encyclopedia of Mathematics and Its Applications. Volume 18. Addison-Wesley, Reading, Mass, USA; 1983:xxii+636.
Goldstein JA: Semigroups of Linear Operators and Applications, Oxford Mathematical Monographs. The Clarendon Press/Oxford University Press, New York, NY, USA; 1985:x+245.
Hille E, Phillips RS: Functional Analysis and Semi-Groups, American Mathematical Society Colloquium Publications, vol. 31. American Mathematical Society, Providence, RI, USA; 1957:xii+808.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, Berlin, Germany; 1983:viii+279.
Acknowledgments
The authors acknowledge the support from the NSF of China (10771202), the Research Fund for Shanghai Key Laboratory of Modern Applied Mathematics (08DZ2271900), and the Specialized Research Fund for the Doctoral Program of Higher Education of China (2007035805).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, Y., Xiao, TJ. & Liang, J. Notes on the Propagators of Evolution Equations. Adv Differ Equ 2010, 795484 (2010). https://doi.org/10.1155/2010/795484
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/795484




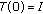 , with (
, with (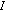 being the identity operator on X) ,
being the identity operator on X) , for
for 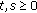 ,
, is continuous on
is continuous on 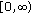 for every
for every 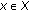 .
.
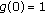 ,
, 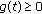 for
for 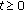 ;
;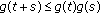 for
for  .
.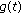 is lower-semicontinuous, that is,
is lower-semicontinuous, that is,

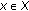 with
with 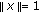 . Thus, taking the supremum for all
. Thus, taking the supremum for all 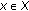 with
with 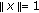 on the left-hand side leads to (2.1).
on the left-hand side leads to (2.1).