Abstract
In 2009, Kim et al. gave some identities of symmetry for the twisted Euler polynomials of higher-order, recently. In this paper, we extend our result to the higher-order twisted  -Euler numbers and polynomials. The purpose of this paper is to establish various identities concerning higher-order twisted
-Euler numbers and polynomials. The purpose of this paper is to establish various identities concerning higher-order twisted  -Euler numbers and polynomials by the properties of
-Euler numbers and polynomials by the properties of  -adic invariant integral on
-adic invariant integral on  . Especially, if
. Especially, if  , we derive the result of Kim et al. (2009).
, we derive the result of Kim et al. (2009).
Similar content being viewed by others
1. Introduction
Let  be a fixed odd prime number. Throughout this paper, the symbols
be a fixed odd prime number. Throughout this paper, the symbols  and
and  will denote the ring of rational integers, the ring of
will denote the ring of rational integers, the ring of  adic integers, the field of
adic integers, the field of  adic rational numbers, the complex number field, and the completion of the algebraic closure of
adic rational numbers, the complex number field, and the completion of the algebraic closure of  , respectively. Let
, respectively. Let  be the set of natural numbers and
be the set of natural numbers and  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with 
When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex
is variously considered as an indeterminate, a complex  , or a
, or a  -adic number
-adic number  . If
. If  one normally assumes that
one normally assumes that  . If
. If  , then we assume that
, then we assume that  so that
so that  for each
for each  We use the following notation:
We use the following notation:

For a fixed positive integer  with
with  , set
, set

where  satisfies the condition
satisfies the condition  For any
For any 

(see [1–13]) is known to be a distribution on  .
.
We say that  is a uniformly differentiable function at
is a uniformly differentiable function at  and denote this property by
and denote this property by  if the difference quotients
if the difference quotients

have a limit  as
as 
For  the fermionic
the fermionic  -adic invariant
-adic invariant  -integral on
-integral on  is defined as
is defined as

(see [14]). Let us define the fermionic  -adic invariant integral on
-adic invariant integral on  as follows:
as follows:

(see [1–12, 14–20]). From the definition of  integral, we have
integral, we have

For  , let
, let  be the
be the  adic locally constant space defined by
adic locally constant space defined by

where  for some
for some  is the cyclic group of order
is the cyclic group of order 
It is well known that the twisted  Euler polynomials of order
Euler polynomials of order  are defined as
are defined as

and  are called the twisted
are called the twisted  Euler numbers of order
Euler numbers of order  When
When  the polynomials and numbers are called the twisted
the polynomials and numbers are called the twisted  Euler polynomials and numbers, respectively. When
Euler polynomials and numbers, respectively. When  and
and  , the polynomials and numbers are called the twisted Euler polynomials and numbers, respectively. When
, the polynomials and numbers are called the twisted Euler polynomials and numbers, respectively. When  ,
,  and
and  , the polynomials and numbers are called the ordinary Euler polynomials and numbers, respectively.
, the polynomials and numbers are called the ordinary Euler polynomials and numbers, respectively.
In [15], Kim et al. gave some identities of symmetry for the twisted Euler polynomials of higher order, recently. In this paper, we extend our result to the higher-order twisted  Euler numbers and polynomials.
Euler numbers and polynomials.
The purpose of this paper is to establish various identities concerning higher-order twisted  -Euler numbers and polynomials by the properties of
-Euler numbers and polynomials by the properties of  adic invariant integral on
adic invariant integral on  . Especially, if
. Especially, if  , we derive the result of [15].
, we derive the result of [15].
2. Some Identities of the Higher-Order Twisted  Euler Numbers and Polynomials
Euler Numbers and Polynomials
Let  with
with  and
and  .
.
For  and
and  , we set
, we set

where

In (2.1), we note that  is symmetric in
is symmetric in  and
and  .
.
From (2.1), we derive that

From the definition of  integral, we also see that
integral, we also see that

It is easy to see that

where  .
.
From (2.3), (2.4), and (2.5), we can derive

From the symmetry of  in
in  and
and  , we also see that
, we also see that

Comparing the coefficients on the both sides of (2.6) and (2.7), we obtain an identity for the twisted  Euler polynomials of higher order as follows.
Euler polynomials of higher order as follows.
Theorem 2.1.
Let  with
with  and
and  .
.
For  and
and  we have
we have

Remark 2.2.
Taking  and
and  in Theorem 2.1, we can derive the following identity:
in Theorem 2.1, we can derive the following identity:

Moreover, if we take  and
and  in Theorem 2.1, then we have the following identity for the twisted
in Theorem 2.1, then we have the following identity for the twisted  Euler numbers of higher order.
Euler numbers of higher order.
Corollary 2.3.
Let  with
with  and
and  . For
. For  and
and  we have
we have

We also note that taking  in Corollary
in Corollary  shows the following identity:
shows the following identity:

Now we will derive another interesting identities for the twisted  -Euler numbers and polynomials of higher order. From (2.3), we can derive that
-Euler numbers and polynomials of higher order. From (2.3), we can derive that

From the symmetry of  in
in  and
and  , we see that
, we see that

Comparing the coefficients on the both sides of (2.12) and (2.13), we obtain the following theorem which shows the relationship between the power sums and the twisted  Euler polynomials.
Euler polynomials.
Theorem 2.4.
Let  with
with  and
and  For
For  and
and  we have
we have

Remark 2.5.
Let  and
and  in Theorem
in Theorem  Then it follows that
Then it follows that

Moreover, if we take  and
and  in Theorem 2.4, then we have the following identity for the twisted
in Theorem 2.4, then we have the following identity for the twisted  Euler numbers of higher order.
Euler numbers of higher order.
Corollary 2.6.
Let  with
with 
 For
For  and
and  we have
we have

If we take  in Corollary 2.3, we derive the following identity for the twisted
in Corollary 2.3, we derive the following identity for the twisted  Euler polynomials: for
Euler polynomials: for  with
with 
 and
and 

Remark 2.7.
If  we can observe the result of [15].
we can observe the result of [15].
References
Kim T:
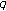 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.Kim T, Choi JY, Sug JY:Extended
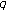 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic 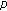 -adic
-adic  -integral on
-integral on 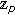 . Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045
. Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045Kim T:Symmetry of power sum polynomials and multivariate fermionic
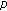 -adic invariant integral on
-adic invariant integral on 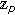 . Russian Journal of Mathematical Physics 2009,16(1):93-96. 10.1134/S1061920809010063
. Russian Journal of Mathematical Physics 2009,16(1):93-96. 10.1134/S1061920809010063Kim T:On
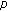 -adic interpolating function for
-adic interpolating function for  -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027Agarwal RP, Ryoo CS:Numerical computations of the roots of the generalized twisted
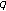 -Bernoulli polynomials. Neural, Parallel & Scientific Computations 2007,15(2):193-206.
-Bernoulli polynomials. Neural, Parallel & Scientific Computations 2007,15(2):193-206.Cenkci M, Can M, Kurt V:
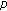 -adic interpolation functions and Kummer-type congruences for
-adic interpolation functions and Kummer-type congruences for  -twisted and
-twisted and 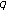 -generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.
-generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.Howard FT: Applications of a recurrence for the Bernoulli numbers. Journal of Number Theory 1995,52(1):157-172. 10.1006/jnth.1995.1062
Kupershmidt BA:Reflection symmetries of
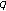 -Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412-422. 10.2991/jnmp.2005.12.s1.34
-Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412-422. 10.2991/jnmp.2005.12.s1.34Ozden H, Simsek Y:Interpolation function of the
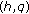 -extension of twisted Euler numbers. Computers & Mathematics with Applications 2008,56(4):898-908. 10.1016/j.camwa.2008.01.020
-extension of twisted Euler numbers. Computers & Mathematics with Applications 2008,56(4):898-908. 10.1016/j.camwa.2008.01.020Jang L-C:A study on the distribution of twisted
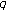 -Genocchi polynomials. Advanced Studies in Contemporary Mathematics 2009,18(2):181-189.
-Genocchi polynomials. Advanced Studies in Contemporary Mathematics 2009,18(2):181-189.Schork M:Ward's "calculus of sequences",
 -calculus and the limit
-calculus and the limit  . Advanced Studies in Contemporary Mathematics 2006,13(2):131-141.
. Advanced Studies in Contemporary Mathematics 2006,13(2):131-141.Tuenter HJH: A symmetry of power sum polynomials and Bernoulli numbers. The American Mathematical Monthly 2001,108(3):258-261. 10.2307/2695389
Kim T:Note on the Euler
 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007Kim T:Symmetry
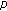 -adic invariant integral on
-adic invariant integral on 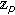 for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220
for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220Kim T, Park KH, Hwang K-W:On the identities of symmetry for the
 -Euler polynomials of higher order. Advances in Difference Equations 2009, 2009:-9.
-Euler polynomials of higher order. Advances in Difference Equations 2009, 2009:-9.Kim T: Note on the Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(2):131-136.
Kim T:Note on
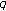 -Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.
-Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.Kim T:The modified
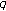 -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170.
-Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170.Kim T:On a
 -analogue of the
-analogue of the 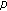 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373Kim T:
 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Moon, EJ., Rim, SH., Jin, JH. et al. On the Symmetric Properties of Higher-Order Twisted 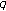 -Euler Numbers and Polynomials.
Adv Differ Equ 2010, 765259 (2010). https://doi.org/10.1155/2010/765259
-Euler Numbers and Polynomials.
Adv Differ Equ 2010, 765259 (2010). https://doi.org/10.1155/2010/765259
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/765259



 Euler Numbers and Polynomials
Euler Numbers and Polynomials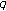 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.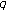 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic 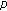 -adic
-adic  -integral on
-integral on 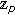 . Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045
. Russian Journal of Mathematical Physics 2007,14(2):160-163. 10.1134/S1061920807020045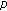 -adic invariant integral on
-adic invariant integral on 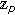 . Russian Journal of Mathematical Physics 2009,16(1):93-96. 10.1134/S1061920809010063
. Russian Journal of Mathematical Physics 2009,16(1):93-96. 10.1134/S1061920809010063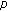 -adic interpolating function for
-adic interpolating function for  -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027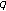 -Bernoulli polynomials. Neural, Parallel & Scientific Computations 2007,15(2):193-206.
-Bernoulli polynomials. Neural, Parallel & Scientific Computations 2007,15(2):193-206.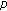 -adic interpolation functions and Kummer-type congruences for
-adic interpolation functions and Kummer-type congruences for  -twisted and
-twisted and 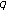 -generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.
-generalized twisted Euler numbers. Advanced Studies in Contemporary Mathematics 2004,9(2):203-216.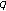 -Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412-422. 10.2991/jnmp.2005.12.s1.34
-Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412-422. 10.2991/jnmp.2005.12.s1.34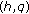 -extension of twisted Euler numbers. Computers & Mathematics with Applications 2008,56(4):898-908. 10.1016/j.camwa.2008.01.020
-extension of twisted Euler numbers. Computers & Mathematics with Applications 2008,56(4):898-908. 10.1016/j.camwa.2008.01.020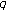 -Genocchi polynomials. Advanced Studies in Contemporary Mathematics 2009,18(2):181-189.
-Genocchi polynomials. Advanced Studies in Contemporary Mathematics 2009,18(2):181-189. -calculus and the limit
-calculus and the limit  . Advanced Studies in Contemporary Mathematics 2006,13(2):131-141.
. Advanced Studies in Contemporary Mathematics 2006,13(2):131-141. -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007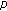 -adic invariant integral on
-adic invariant integral on 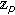 for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220
for Bernoulli and Euler polynomials. Journal of Difference Equations and Applications 2008,14(12):1267-1277. 10.1080/10236190801943220 -Euler polynomials of higher order. Advances in Difference Equations 2009, 2009:-9.
-Euler polynomials of higher order. Advances in Difference Equations 2009, 2009:-9.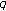 -Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.
-Genocchi numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,17(1):9-15.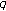 -Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170.
-Euler numbers and polynomials. Advanced Studies in Contemporary Mathematics 2008,16(2):161-170. -analogue of the
-analogue of the 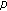 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.