Abstract
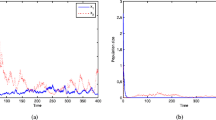
A discrete predator-prey system with time delay and feedback controls is studied. Sufficient conditions which guarantee the predator and the prey to be permanent are obtained. Moreover, under some suitable conditions, we show that the predator species y will be driven to extinction. The results indicate that one can choose suitable controls to make the species coexistence in a long term.
Similar content being viewed by others
1. Introduction
The dynamic relationship between predator and its prey has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance. The traditional predator-prey models have been studied extensively (e.g., see [1–10] and references cited therein), but they are questioned by several biologists. Thus, the Lotka-Volterra type predator-prey model with the Beddington-DeAngelis functional response has been proposed and has been well studied. The model can be expressed as follows:

The functional response in system (1.1) was introduced by Beddington [11] and DeAngelis et al. [12]. It is similar to the well-known Holling type II functional response but has an extra term  in the denominator which models mutual interference between predators. It can be derived mechanistically from considerations of time utilization [11] or spatial limits on predation. But few scholars pay attention to this model. Hwang [6] showed that the system has no periodic solutions when the positive equilibrium is locally asymptotical stability by using the divergency criterion. Recently, Fan and Kuang [9] further considered the nonautonomous case of system (1.1), that is, they considered the following system:
in the denominator which models mutual interference between predators. It can be derived mechanistically from considerations of time utilization [11] or spatial limits on predation. But few scholars pay attention to this model. Hwang [6] showed that the system has no periodic solutions when the positive equilibrium is locally asymptotical stability by using the divergency criterion. Recently, Fan and Kuang [9] further considered the nonautonomous case of system (1.1), that is, they considered the following system:

For the general nonautonomous case, they addressed properties such as permanence, extinction, and globally asymptotic stability of the system. For the periodic (almost periodic) case, they established sufficient criteria for the existence, uniqueness, and stability of a positive periodic solution and a boundary periodic solution. At the end of their paper, numerical simulation results that complement their analytical findings were present.
However, we note that ecosystem in the real world is continuously disturbed by unpredictable forces which can result in changes in the biological parameters such as survival rates. Of practical interest in ecosystem is the question of whether an ecosystem can withstand those unpredictable forces which persist for a finite period of time or not. In the language of control variables, we call the disturbance functions as control variables. In 1993, Gopalsamy and Weng [13] introduced a control variable into the delay logistic model and discussed the asymptotic behavior of solution in logistic models with feedback controls, in which the control variables satisfy certain differential equation. In recent years, the population dynamical systems with feedback controls have been studied in many papers, for example, see [13–22] and references cited therein.
It has been found that discrete time models governed by difference equations are more appropriate than the continuous ones when the populations have nonoverlapping generations. Discrete time models can also provide efficient computational models of continuous models for numerical simulations. It is reasonable to study discrete models governed by difference equations. Motivated by the above works, we focus our attention on the permanence and extinction of species for the following nonautonomous predator-prey model with time delay and feedback controls:

where  ,
,  are the density of the prey species and the predator species at time
are the density of the prey species and the predator species at time  , respectively.
, respectively.  ,
, are the feedback control variables.
are the feedback control variables.  represent the intrinsic growth rate and density-dependent coefficient of the prey at time
represent the intrinsic growth rate and density-dependent coefficient of the prey at time  , respectively.
, respectively.  denote the death rate and density-dependent coefficient of the predator at time
denote the death rate and density-dependent coefficient of the predator at time  , respectively.
, respectively.  denotes the capturing rate of the predator;
denotes the capturing rate of the predator;  represents the rate of conversion of nutrients into the reproduction of the predator. Further,
represents the rate of conversion of nutrients into the reproduction of the predator. Further,  is a positive integer.
is a positive integer.
For the simplicity and convenience of exposition, we introduce the following notations. Let  ,
,  and
and  denote the set of integer
denote the set of integer  satisfying
satisfying  We denote
We denote  to be the space of all nonnegative and bounded discrete time functions. In addition, for any bounded sequence
to be the space of all nonnegative and bounded discrete time functions. In addition, for any bounded sequence  we denote
we denote  ,
, 
Given the biological sense, we only consider solutions of system (1.3) with the following initial condition:

It is not difficult to see that the solutions of system (1.3) with the above initial condition are well defined for all  and satisfy
and satisfy

The main purpose of this paper is to establish a new general criterion for the permanence and extinction of system (1.3), which is dependent on feedback controls. This paper is organized as follows. In Section 2, we will give some assumptions and useful lemmas. In Section 3, some new sufficient conditions which guarantee the permanence of all positive solutions of system (1.3) are obtained. Moreover, under some suitable conditions, we show that the predator species  will be driven to extinction.
will be driven to extinction.
2. Preliminaries
In this section, we present some useful assumptions and state several lemmas which will be useful in the proving of the main results.
Throughout this paper, we will have both of the following assumptions:
( )
)  ,
,  ,
,  ,
,  and
and  are nonnegative bounded sequences of real numbers defined on
are nonnegative bounded sequences of real numbers defined on  such that
such that


 ,
,  ,
,  and
and  are nonnegative bounded sequences of real numbers defined on
are nonnegative bounded sequences of real numbers defined on  such that
such that

Now, we state several lemmas which will be used to prove the main results in this paper.
First, we consider the following nonautonomous equation:

where functions  ,
,  are bounded and continuous defined on
are bounded and continuous defined on  with
with  ,
,  . We have the following result which is given in [23].
. We have the following result which is given in [23].
Lemma 2.1.
Let  be the positive solution of (2.3) with
be the positive solution of (2.3) with  , then
, then
-
(a)
there exists a positive constant
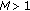 such that
such that

for any positive solution  of (2.3);
of (2.3);
-
(b)
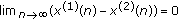 for any two positive solutions
for any two positive solutions  and
and 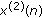 of (2.3).
of (2.3).
Second, one considers the following nonautonomous linear equation:

where functions  and
and  are bounded and continuous defined on
are bounded and continuous defined on  with
with  and
and  The following Lemma 2.2 is a direct corollary of Theorem
The following Lemma 2.2 is a direct corollary of Theorem  of L. Wang and M. Q. Wang [24, page 125].
of L. Wang and M. Q. Wang [24, page 125].
Lemma 2.2.
Let  be the nonnegative solution of (2.5) with
be the nonnegative solution of (2.5) with  , then
, then
-
(a)
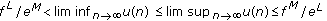 for any positive solution
for any positive solution  of (2.5);
of (2.5); -
(b)
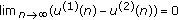 for any two positive solutions
for any two positive solutions  and
and  of (2.5).
of (2.5).
Further, considering the following:

where functions  and
and  are bounded and continuous defined on
are bounded and continuous defined on  with
with  ,
,  and
and  The following Lemma 2.3 is a direct corollary of Lemma
The following Lemma 2.3 is a direct corollary of Lemma  of Xu and Teng [25].
of Xu and Teng [25].
Lemma 2.3.
Let  be the positive solution of (2.6) with
be the positive solution of (2.6) with  , then for any constants
, then for any constants  and
and  , there exist positive constants
, there exist positive constants  and
and  such that for any
such that for any  and
and  when
when  one has
one has

where  is a positive solution of (2.5) with
is a positive solution of (2.5) with 
Finally, one considers the following nonautonomous linear equation:

where functions  are bounded and continuous defined on
are bounded and continuous defined on  with
with  and
and  In [25], the following Lemma 2.4 has been proved.
In [25], the following Lemma 2.4 has been proved.
Lemma 2.4.
Let  be the nonnegative solution of (2.8) with
be the nonnegative solution of (2.8) with  , then, for any constants
, then, for any constants  and
and  , there exist positive constants
, there exist positive constants  and
and  such that for any
such that for any  and
and  when
when  , one has
, one has

3. Main Results
Theorem 3.1.
Suppose that assumptions  and
and  hold, then there exists a constant
hold, then there exists a constant  such that
such that

for any positive solution  of system (1.3).
of system (1.3).
Proof.
Given any solution  of system (1.3), we have
of system (1.3), we have

for all  where
where  is the initial time.
is the initial time.
Consider the following auxiliary equation:

from assumptions 
 and Lemma 2.2, there exists a constant
and Lemma 2.2, there exists a constant  such that
such that

where  is the solution of (3.3) with initial condition
is the solution of (3.3) with initial condition  By the comparison theorem, we have
By the comparison theorem, we have

From this, we further have

Then, we obtain that for any constant  there exists a constant
there exists a constant  such that
such that

According to the first equation of system (1.3), we have

for all  Considering the following auxiliary equation:
Considering the following auxiliary equation:

thus, as a direct corollary of Lemma 2.1, we get that there exists a positive constant  such that
such that

where  is the solution of (3.9) with initial condition
is the solution of (3.9) with initial condition  By the comparison theorem, we have
By the comparison theorem, we have

From this, we further have

Then, we obtain that for any constant  there exists a constant
there exists a constant  such that
such that

Hence, from the second equation of system (1.3), we obtain

for all  Following a similar argument as above, we get that there exists a positive constant
Following a similar argument as above, we get that there exists a positive constant  such that
such that

By a similar argument of the above proof, we further obtain

From (3.6) and (3.12)–(3.16), we can choose the constant  , such that
, such that

This completes the proof of Theorem 3.1.
In order to obtain the permanence of system (1.3), we assume that
 (
( )
)  where
where  is some positive solution of the following equation:
is some positive solution of the following equation:

Theorem 3.2.
Suppose that assumptions  hold, then there exists a constant
hold, then there exists a constant  such that
such that

for any positive solution  of system (1.3).
of system (1.3).
Proof.
According to assumptions  and
and  we can choose positive constants
we can choose positive constants  and
and  such that
such that

Consider the following equation with parameter  :
:

Let  be any positive solution of system (3.18) with initial value
be any positive solution of system (3.18) with initial value  By assumptions
By assumptions  and Lemma 2.2, we obtain that
and Lemma 2.2, we obtain that  is globally asymptotically stable and converges to
is globally asymptotically stable and converges to  uniformly for
uniformly for  Further, from Lemma 2.3, we obtain that, for any given
Further, from Lemma 2.3, we obtain that, for any given  and a positive constant
and a positive constant  (
( is given in Theorem 3.1), there exist constants
is given in Theorem 3.1), there exist constants  and
and  such that for any
such that for any  and
and  when
when  , we have
, we have

where  is the solution of (3.21) with initial condition
is the solution of (3.21) with initial condition 
Let  from (3.20), we obtain that there exist
from (3.20), we obtain that there exist  and
and  such that
such that

for all 
We first prove that

for any positive solution  of system (1.3). In fact, if (3.24) is not true, then there exists a
of system (1.3). In fact, if (3.24) is not true, then there exists a  such that
such that

where  is the solution of system (1.3) with initial condition
is the solution of system (1.3) with initial condition  ,
,  So, there exists an
So, there exists an  such that
such that

Hence, (3.26) together with the third equation of system (1.3) lead to

for  Let
Let  be the solution of (3.21) with initial condition
be the solution of (3.21) with initial condition  by the comparison theorem, we have
by the comparison theorem, we have

In (3.22), we choose  and
and  since
since  then for given
then for given  we have
we have

for all  Hence, from (3.28), we further have
Hence, from (3.28), we further have

From the second equation of system (1.3), we have

for all  Obviously, we have
Obviously, we have  as
as  Therefore, we get that there exists an
Therefore, we get that there exists an  such that
such that

for any  Hence, by (3.26), (3.30), and (3.32), it follows that
Hence, by (3.26), (3.30), and (3.32), it follows that

for any  where
where  Thus, from (3.23) and (3.33), we have
Thus, from (3.23) and (3.33), we have  which leads to a contradiction. Therefore, (3.24) holds.
which leads to a contradiction. Therefore, (3.24) holds.
Now, we prove the conclusion of Theorem 3.2. In fact, if it is not true, then there exists a sequence  of initial functions such that
of initial functions such that

On the other hand, by (3.24), we have

Hence, there are two positive integer sequences  and
and  satisfying
satisfying

and  such that
such that


By Theorem 3.1, for any given positive integer  , there exists a
, there exists a  such that
such that  ,
,  ,
,  , and
, and  for all
for all  Because of
Because of  as
as  there exists a positive integer
there exists a positive integer  such that
such that  and
and  as
as  Let
Let  for any
for any  , we have
, we have

where  Hence,
Hence,

The above inequality implies that

So, we can choose a large enough  such that
such that

From the third equation of system (1.3) and (3.38), we have

for any  ,
,  , and
, and  Assume that
Assume that  is the solution of (3.21) with the initial condition
is the solution of (3.21) with the initial condition  , then from comparison theorem and the above inequality, we have
, then from comparison theorem and the above inequality, we have

In (3.22), we choose  and
and  , since
, since  and
and  , then for all
, then for all  , we have
, we have

Equation (3.44) together with (3.45) lead to

for all  ,
,  and
and  .
.
From the second equation of system(1.3), we have

for  ,
,  , and
, and  Therefore, we get that
Therefore, we get that

for any  Further, from the first equation of systems (1.3), (3.46), and (3.48), we obtain
Further, from the first equation of systems (1.3), (3.46), and (3.48), we obtain

for any  ,
,  , and
, and  Hence,
Hence,

In view of (3.37) and (3.38), we finally have

which is a contradiction. Therefore, the conclusion of Theorem 3.2 holds. This completes the proof of Theorem 3.2.
In order to obtain the permanence of the component  of system (1.3), we next consider the following single-specie system with feedback control:
of system (1.3), we next consider the following single-specie system with feedback control:

For system (3.52), we further introduce the following assumption:
 suppose
suppose  ,
,  where
where  ,
,  are given in the proof of Lemma 3.3.
are given in the proof of Lemma 3.3.
For system(3.52), we have the following result.
Lemma 3.3.
Suppose that assumptions  hold, then
hold, then
-
(a)
there exists a constant
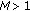 such that
such that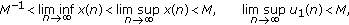 (3.53)
(3.53)for any positive solution
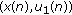 of system (3.52).
of system (3.52). -
(b)
if assumption
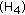 holds, then each fixed positive solution
holds, then each fixed positive solution 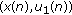 of system (3.52) is globally uniformly attractive on
of system (3.52) is globally uniformly attractive on 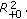
Proof.
Based on assumptions  , conclusion (a) can be proved by a similar argument as in Theorems 3.1 and 3.2.
, conclusion (a) can be proved by a similar argument as in Theorems 3.1 and 3.2.
Here, we prove conclusion (b). Letting  be some solution of system (3.52), by conclusion (a), there exist constants
be some solution of system (3.52), by conclusion (a), there exist constants  ,
,  , and
, and  , such that
, such that

for any solution  of system (3.52) and
of system (3.52) and  We make transformation
We make transformation  and
and  Hence, system (3.52) is equivalent to
Hence, system (3.52) is equivalent to

According to  , there exists a
, there exists a  small enough, such that
small enough, such that  ,
,  Noticing that
Noticing that  implies that
implies that  lie between
lie between  and
and  Therefore,
Therefore,  ,
,  It follows from (3.55) that
It follows from (3.55) that

Let  then
then  . It follows easily from (3.56) that
. It follows easily from (3.56) that

Therefore,  as
as  and we can easily obtain that
and we can easily obtain that  and
and  The proof is completed.
The proof is completed.
Considering the following equations:

then we have the following result.
Lemma 3.4.
Suppose that assumptions  hold, then there exists a positive constant
hold, then there exists a positive constant  such that for any positive solution
such that for any positive solution  of system (3.58), one has
of system (3.58), one has

where  is the solution of system (3.52) with
is the solution of system (3.52) with  and
and 
The proof of Lemma 3.4 is similar to Lemma 3.3, one omits it here.
Let  be a fixed solution of system (3.52) defined on
be a fixed solution of system (3.52) defined on  one assumes that
one assumes that


Theorem 3.5.
Suppose that assumptions  hold, then there exists a constant
hold, then there exists a constant  such that
such that

for any positive solution  of system (1.3).
of system (1.3).
Proof.
According to assumption  we can choose positive constants
we can choose positive constants  ,
,  , and
, and  , such that for all
, such that for all  we have
we have

Considering the following equation with parameter  :
:

by Lemma 2.4, for given  and
and  (
( is given in Theorem 3.1.), there exist constants
is given in Theorem 3.1.), there exist constants  and
and  , such that for any
, such that for any  and
and  when
when  we have
we have

We choose  if there exists a constant
if there exists a constant  such that
such that  for all
for all  otherwise
otherwise  Obviously, there exists an
Obviously, there exists an  , such that
, such that

Now, We prove that

for any positive solution  of system (1.3). In fact, if (3.65) is not true, then for
of system (1.3). In fact, if (3.65) is not true, then for  , there exist a
, there exist a  and
and  such that for all
such that for all 

where  and
and  Hence, for all
Hence, for all  one has
one has

Therefore, from system (1.3), Lemmas 3.3 and 3.4, it follows that

for any solution  of system (1.3). Therefore, for any small positive constant
of system (1.3). Therefore, for any small positive constant  there exists an
there exists an  such that for all
such that for all  we have
we have

From the fourth equation of system (1.3), one has

In (3.63), we choose  and
and  Since
Since  then for all
then for all  , we have
, we have

Equations (3.69), (3.71) together with the second equation of system (1.3) lead to

for all  where
where  Obviously, we have
Obviously, we have  as
as  which is contradictory to the boundedness of solution of system (1.3). Therefore, (3.65) holds.
which is contradictory to the boundedness of solution of system (1.3). Therefore, (3.65) holds.
Now, we prove the conclusion of Theorem 3.5. In fact, if it is not true, then there exists a sequence  of initial functions, such that
of initial functions, such that

where  is the solution of system (1.3) with initial condition
is the solution of system (1.3) with initial condition  for all
for all  On the other hand, it follows from (3.65) that
On the other hand, it follows from (3.65) that

Hence, there are two positive integer sequences  and
and  satisfying
satisfying

and  such that
such that


By Theorem 3.1, for given positive integer  , there exists a
, there exists a  such that
such that  ,
,  ,
,  , and
, and  for all
for all  Because that
Because that  as
as  there is a positive integer
there is a positive integer  such that
such that  and
and  as
as  Let
Let  for any
for any  , we have
, we have

where  Hence,
Hence,

The above inequality implies that

Choosing a large enough  such that
such that

then for  we have
we have

for all  Therefore, it follows from system (1.3) that
Therefore, it follows from system (1.3) that

for all  Further, by Lemmas 3.3 and 3.4, we obtain that for any small positive constant
Further, by Lemmas 3.3 and 3.4, we obtain that for any small positive constant  we have
we have

for any  ,
,  , and
, and  For any
For any  ,
,  , and
, and  by the first equation of systems (1.3) and (3.77), it follows that
by the first equation of systems (1.3) and (3.77), it follows that

Assume that  is the solution of (3.62) with the initial condition
is the solution of (3.62) with the initial condition  , then from comparison theorem and the above inequality, we have
, then from comparison theorem and the above inequality, we have

In (3.63), we choose  and
and  Since
Since  and
and  then we have
then we have

Equation (3.86) together with (3.87) lead to

for all  ,
,  , and
, and  .
.
So, for any  ,
,  , and
, and  from the second equation of systems (1.3), (3.61), (3.77), (3.84), and (3.88), it follows that
from the second equation of systems (1.3), (3.61), (3.77), (3.84), and (3.88), it follows that

Hence,

In view of (3.76) and (3.77), we finally have

which is a contradiction. Therefore, the conclusion of Theorem 3.5 holds.
Remark 3.6.
In Theorems 3.2 and 3.5, we note that  are decided by system(1.3), which is dependent on the feedback control
are decided by system(1.3), which is dependent on the feedback control  . So, the control variable
. So, the control variable  has impact on the permanence of system (1.3). That is, there is the permanence of the species as long as feedback controls should be kept beyond the range. If not, we have the following result.
has impact on the permanence of system (1.3). That is, there is the permanence of the species as long as feedback controls should be kept beyond the range. If not, we have the following result.
Theorem 3.7.
Suppose that assumption

holds, then

for any positive solution  of system (1.3).
of system (1.3).
Proof.
By the condition, for any positive constant  (
( where
where  is given in Theorem 3.5), there exist constants
is given in Theorem 3.5), there exist constants  and
and  such that
such that

for  First, we show that there exists an
First, we show that there exists an  such that
such that  Otherwise, there exists an
Otherwise, there exists an  , such that
, such that

Hence, for all  one has
one has

Therefore, from Lemma 3.3 and comparison theorem, it follows that for the above  there exists an
there exists an  , such that
, such that

Hence, for  we have
we have

So,  which is a contradiction. Therefor, there exists an
which is a contradiction. Therefor, there exists an  such that
such that 
Second, we show that

where

is bounded. Otherwise, there exists an  such that
such that  Hence, there must exist an
Hence, there must exist an  such that
such that  ,
,  , and
, and  for
for  Let
Let  be a nonnegative integer, such that
be a nonnegative integer, such that

It follows from (3.101) that

which leads to a contradiction. This shows that (3.99) holds. By the arbitrariness of  it immediately follows that
it immediately follows that  as
as  This completes the proof of Theorem 3.7.
This completes the proof of Theorem 3.7.
References
Cantrell RS, Cosner C: On the dynamics of predator-prey models with the Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications 2001,257(1):206-222. 10.1006/jmaa.2000.7343
Cosner NP, deAngelis DL, Ault JS, Olson DB: Effects of spatial grouping on the functional response of predators. Theoretical Population Biology 1999, 56: 65-75. 10.1006/tpbi.1999.1414
Cui J, Takeuchi Y: Permanence, extinction and periodic solution of predator-prey system with Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications 2006,317(2):464-474. 10.1016/j.jmaa.2005.10.011
Dimitrov DT, Kojouharov HV: Complete mathematical analysis of predator-prey models with linear prey growth and Beddington-DeAngelis functional response. Applied Mathematics and Computation 2005,162(2):523-538. 10.1016/j.amc.2003.12.106
Huo H-F, Li W-T, Nieto JJ: Periodic solutions of delayed predator-prey model with the Beddington-DeAngelis functional response. Chaos, Solitons and Fractals 2007,33(2):505-512. 10.1016/j.chaos.2005.12.045
Hwang T-W: Global analysis of the predator-prey system with Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications 2003,281(1):395-401. 10.1016/S0022-247X(02)00395-5
Kar TK, Pahari UK: Modelling and analysis of a prey-predator system with stage-structure and harvesting. Nonlinear Analysis. Real World Applications 2007,8(2):601-609. 10.1016/j.nonrwa.2006.01.004
Li Z, Wang W, Wang H: The dynamics of a Beddington-type system with impulsive control strategy. Chaos, Solitons and Fractals 2006,29(5):1229-1239. 10.1016/j.chaos.2005.08.195
Fan M, Kuang Y: Dynamics of a nonautonomous predator-prey system with the Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications 2004,295(1):15-39. 10.1016/j.jmaa.2004.02.038
Yang X: Uniform persistence and periodic solutions for a discrete predator-prey system with delays. Journal of Mathematical Analysis and Applications 2006,316(1):161-177. 10.1016/j.jmaa.2005.04.036
Beddington JR: Mutual interference between parasites or predators and its effect on searching efficiency. Journal of Animal Ecology 1975, 44: 331-340. 10.2307/3866
deAngelis DL, Goldstein RA, O'Neill RV: A model for trophic interaction. Ecology 1975, 56: 881-892. 10.2307/1936298
Gopalsamy K, Weng PX: Feedback regulation of logistic growth. International Journal of Mathematics and Mathematical Sciences 1993,16(1):177-192. 10.1155/S0161171293000213
Chen F: Positive periodic solutions of neutral Lotka-Volterra system with feedback control. Applied Mathematics and Computation 2005,162(3):1279-1302. 10.1016/j.amc.2004.03.009
Huo H-F, Li W-T: Positive periodic solutions of a class of delay differential system with feedback control. Applied Mathematics and Computation 2004,148(1):35-46. 10.1016/S0096-3003(02)00824-X
Weng P: Existence and global stability of positive periodic solution of periodic integrodifferential systems with feedback controls. Computers & Mathematics with Applicationsl 2000,40(6-7):747-759. 10.1016/S0898-1221(00)00193-0
Wang K, Teng Z, Jiang H:On the permanence for
 -species non-autonomous Lotka-Volterra competitive system with infinite delays and feedback controls. International Journal of Biomathematics 2008,1(1):29-43. 10.1142/S1793524508000060
-species non-autonomous Lotka-Volterra competitive system with infinite delays and feedback controls. International Journal of Biomathematics 2008,1(1):29-43. 10.1142/S1793524508000060Chen F, Yang J, Chen L, Xie X: On a mutualism model with feedback controls. Applied Mathematics and Computation 2009,214(2):581-587. 10.1016/j.amc.2009.04.019
Fan Y-H, Wang L-L: Permanence for a discrete model with feedback control and delay. Discrete Dynamics in Nature and Society 2008, 2008:-8.
Li Y, Zhu L: Existence of positive periodic solutions for difference equations with feedback control. Applied Mathematics Letters 2005,18(1):61-67. 10.1016/j.aml.2004.09.002
Chen L, Li Z: Permanence of a delayed discrete mutualism model with feedback controls. Mathematical and Computer Modelling 2009,50(7-8):1083-1089. 10.1016/j.mcm.2009.02.015
Chen F: The permanence and global attractivity of Lotka-Volterra competition system with feedback controls. Nonlinear Analysis 2006,7(1):133-143. 10.1016/j.nonrwa.2005.01.006
Zhou Z, Zou X: Stable periodic solutions in a discrete periodic logistic equation. Applied Mathematics Letters 2003,16(2):165-171. 10.1016/S0893-9659(03)80027-7
Wang L, Wang MQ: Ordinary Difference Equation. Xinjiang University Press, Urumqi, China; 1991.
Xu J, Teng Z: Permanence for a nonautonomous discrete single-species system with delays and feedback control. Applied Mathematics Letters 2010,23(9):949-954. 10.1016/j.aml.2009.12.008
Acknowledgments
This work was supported by the National Sciences Foundation of China (no. 11071283) and the Sciences Foundation of Shanxi (no. 2009011005-3).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Q., Liu, H. & Zhang, F. The Permanence and Extinction of a Discrete Predator-Prey System with Time Delay and Feedback Controls. Adv Differ Equ 2010, 738306 (2010). https://doi.org/10.1155/2010/738306
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/738306



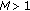 such that
such that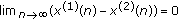 for any two positive solutions
for any two positive solutions  and
and 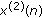 of (2.3).
of (2.3).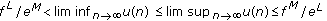 for any positive solution
for any positive solution  of (2.5);
of (2.5);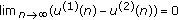 for any two positive solutions
for any two positive solutions  and
and  of (2.5).
of (2.5).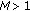 such that
such that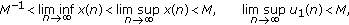
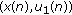 of system (3.52).
of system (3.52).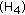 holds, then each fixed positive solution
holds, then each fixed positive solution 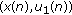 of system (3.52) is globally uniformly attractive on
of system (3.52) is globally uniformly attractive on 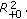
 -species non-autonomous Lotka-Volterra competitive system with infinite delays and feedback controls. International Journal of Biomathematics 2008,1(1):29-43. 10.1142/S1793524508000060
-species non-autonomous Lotka-Volterra competitive system with infinite delays and feedback controls. International Journal of Biomathematics 2008,1(1):29-43. 10.1142/S1793524508000060