Abstract
In subspace-based method for direction-of-arrival (DOA) estimation of signal wavefronts, the additive noise term is often assumed to be spatially white or known to within a multiplicative scalar. When the noise is nonwhite but has a known covariance matrix, we can still handle the problem through prewhitening. However, the problem turns to be complex when the noise field is completely unknown. In this paper, we study the localization of the sources, when the noise covariance matrix is one unknown band matrix. An iterative denoising algorithm based on the noise subspace spanned by the eigenvectors associated with the smallest eigenvalues is developed. The performance of the proposed algorithm is evaluated by computer simulations. We also test the proposed algorithm with some experimental data recorded during an underwater acoustic experiment.
Similar content being viewed by others
1. Introduction
Array processing is used in diverse areas such as radar, sonar, communications, and seismic exploration. Usually the parameters of interest are the directions of arrival of the radiating sources. The high-resolution subspace-based methods for direction-of-arrival (DOA) estimation have been a topic of great interest. The subspace-based methods well-developed so far require a fundamental assumption, which is that the background noise is uncorrelated from sensor to sensor, or known to within a multiplicative scalar. In practice this assumption is rarely fulfilled and the noise received by the array may be a combination of multiple noise sources such as flow noise, traffic noise, or ambient noise, which is often correlated along the array [1, 2]. However, the spatial noise is estimated by measuring the spectrum of the received data when no signal is present. The data for parameter estimation is then prewhitened using the measured noise. The problem with this method is that the actual noise covariance matrix varies as a function of time in many applications. At low signal-to-noise ratio (SNR) the deviations from the assumed noise characteristics are critical and the degradation may be severe for the localization result. A maximum likelihood algorithm is presented in [3], where the spatial noise covariance is modeled as a function of certain unknown parameters. Also in [4, 5] a maximum likelihood estimator is analyzed. The problem of incomplete prewhitening or colored noise is circumvented by modeling the noise with a simple descriptive model. As opposed to AR and ARMA models used in [6] this gives the advantages of incorporating prior knowledge into the model [5, 7]. There are other approaches to the problem of spatially correlated noise: one is based on the assumption that the correlation structure of the noise field is invariant under a rotation or a translation of the array, while another is based on a certain linear transformation of the sensor output vectors [8–13].
In this paper, we present an algorithm to estimate the noise with band covariance matrix. This algorithm is based on the noise subspace spanned by the eigenvectors associated with the smallest eigenvalues of the covariance matrix of the recorded data. The goal of the present study is to investigate how the perturbations due to the noise covariance matrix affect the accuracy of the narrow-band signal DOA estimates [14–18].
The remainder of the paper is as follows. Section 2 presents the high resolution algorithm. Section 3 proposes the model of the additive noise. Section 4 introduces the covariance matrix of the band noise. Section 5 presents the proposed algorithm. Sections 6 and 7 present some comparative results concerning the proposed algorithm exemplified using simulated data and real-world signals in a noisy environment. Section 8 gives the conclusions.
In this paper, we denote by,  a scalar,
a scalar,  a vector, and X a matrix.
a vector, and X a matrix.
2. Problem Formulation
Consider an array of  sensors which receive the signals in one wave field generated by
sensors which receive the signals in one wave field generated by  sources in the presence of an additive noise. The received signal vector is sampled and the DFT algorithm is used to transform the data into the frequency domain. We represent these samples by
sources in the presence of an additive noise. The received signal vector is sampled and the DFT algorithm is used to transform the data into the frequency domain. We represent these samples by

where  ,
,  , and
, and  are, respectively, the Fourier transforms of the array outputs, the source signals, and the noise vectors. The matrix
are, respectively, the Fourier transforms of the array outputs, the source signals, and the noise vectors. The matrix  , with dimensions
, with dimensions  , is the transfer matrix of the source-sensor array systems with respect to some chosen reference point. The sensor noise is assumed to be independent of the source signals and partially spatially correlated. The sources are assumed to be uncorrelated. The covariance matrix of the data can be defined by the
, is the transfer matrix of the source-sensor array systems with respect to some chosen reference point. The sensor noise is assumed to be independent of the source signals and partially spatially correlated. The sources are assumed to be uncorrelated. The covariance matrix of the data can be defined by the  -dimensional matrix
-dimensional matrix


where  denotes the expectation operator, superscript
denotes the expectation operator, superscript  represents conjugate transpose,
represents conjugate transpose,  is the
is the  noise covariance matrix, and
noise covariance matrix, and  is the
is the  signal covariance matrix. The above assumption concerning the noncorrelation of the sources means that
signal covariance matrix. The above assumption concerning the noncorrelation of the sources means that  is full rank.
is full rank.
The high-resolution algorithms of array processing assume that the matrix  is diagonal with constant element. The subspace-based techniques are based on these properties. For example the Multiple Signal Classification (MUSIC) [10] null-spectrum
is diagonal with constant element. The subspace-based techniques are based on these properties. For example the Multiple Signal Classification (MUSIC) [10] null-spectrum  is defined by
is defined by

and it is expected that  has maximum points around
has maximum points around  , where
, where  are the directions of arrival of the sources. Therefore, we can estimate the DOA by taking the local maximum points of
are the directions of arrival of the sources. Therefore, we can estimate the DOA by taking the local maximum points of  .
.
In this paper, we consider that the matrix  is not diagonal because the noise realizations are spatially correlated and then the performances of these methods are considerably degraded [16–19].
is not diagonal because the noise realizations are spatially correlated and then the performances of these methods are considerably degraded [16–19].
3. Modeling the Noise Field
A fundamental limitation of the standard parametric array processing algorithms is that the covariance matrix of background noise cannot, in general, be estimated along with the signal parameters. So this leads to a unidentifiable parametrization, the measured data should always be regarded to consist on only the noise with a covariance matrix equal to that of the observed samples. This is a reason for imposing a model on the background noise. Several parametric noise models have been proposed in some literatures recently. Here, as well as in [8, 20], a descriptive model will be used, that is, the spatial noise covariance matrix is assumed to be a linear combination of some unknown parameters, which are weighted by known basis matrices. There are two different noise phenomenons to be described. We can model the noise as follows.
-
(i)
An internal noise generated by the sensors so-called thermal noise. This noise is assumed to be independent [8, 11] from sensor to sensor, but not necessarily spatially white. Then the spatial covariance matrix of this noise denoted
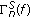 is diagonal.
is diagonal. -
(ii)
An external noise received on the sensors, whose spatial covariance matrix is assumed to have the following structure [8, 11, 12, 19],
 , where
, where  are unknown parameters and
are unknown parameters and  are complex weighting matrices,
are complex weighting matrices, 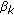 are chosen such that
are chosen such that 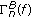 is positive definite and of band structure.
is positive definite and of band structure.
Consequently, the additive noise is the sum of these two noise terms and the spatial covariance matrix is

4. Modeling the Covariance Matrix of the Band Noise
In many applications when a uniform linear array antenna system is used, it is reasonable to assume that noise correlation is decreasing along the array (see Figure 1). This is a widely used model for colored noise. We can then obtain a specific model for noise correlation under the following assumptions:
-
(i)
the correlation length is
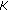 which means that the spatial correlation attains up to the
which means that the spatial correlation attains up to the 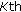 sensor;
sensor; -
(ii)
the noise realizations received by sensors which are separated with a distance no less than
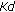 , where
, where  is the distance between sensors, are considered uncorrelated.
is the distance between sensors, are considered uncorrelated.
The noise correlation model which is obtained is represented on Figure 1.
In this paper the noise covariance matrix is modeled as a Hermitian, positive-definite band matrix  , with half-bandwidth
, with half-bandwidth  . The
. The  element of
element of  is
is  with
with

where  ;
;  ,
,  are complex variables,
are complex variables,  ,
,  is the noise variance at the
is the noise variance at the  sensor, and
sensor, and  denotes complex conjugate.
denotes complex conjugate.
In the following section, an algorithm to estimate the band noise covariance matrix is developed for narrow-band signals.
5. Estimation of the Noise Covariance Matrix
5.1. Proposed Algorithm
Several methods have been proposed for estimating the directions of arrival of multiple sources in unknown noise fields. Initially the noise covariance matrix is measured, when signals of interest are not present. Other techniques [5, 7, 21] based on the maximum likelihood algorithm are developed, which incorporate a noise model to reduce the bias for estimating both the noise covariance matrix and the directions of arrival of the sources. In this paper, our approach is realized in two steps. Using an iterative algorithm, the noise covariance matrix is estimated, then this estimate is subtracted from the covariance matrix of the received signals.
As the noise is supposed to be uncorrelated with the source signals, using (3), one can see that  element of
element of

where  is the
is the  element of the matrix
element of the matrix  . These equations show that the element
. These equations show that the element  for
for 
 and
and  is not impaired by the additive noise. We know also that [12]
is not impaired by the additive noise. We know also that [12]

where  is a
is a  diagonal matrix containing the
diagonal matrix containing the  largest eigenvalues and where the
largest eigenvalues and where the  matrix
matrix  contains the
contains the  corresponding eigenvectors of the covariance matrix
corresponding eigenvectors of the covariance matrix  . So, we have
. So, we have


Using (9), we obtain a constraint for estimating correctly the largest eigenvalues and the corresponding eigenvectors. Indeed by minimizing the error  we can estimate the eigen-elements by an iterative algorithm. Then by using (10) we calculate the noise covariance matrix. The proposed method for estimating the noise covariance matrix can be summarized as follows.
we can estimate the eigen-elements by an iterative algorithm. Then by using (10) we calculate the noise covariance matrix. The proposed method for estimating the noise covariance matrix can be summarized as follows.
Step 1.
Estimate the covariance matrix  of the received signals using
of the received signals using  snapshots:
snapshots:  . Calculate the eigendecomposition of this matrix:
. Calculate the eigendecomposition of this matrix:  with
with  and
and  , where
, where  , and
, and  are, respectively, the
are, respectively, the  eigenvalue and the corresponding eigenvector.
eigenvalue and the corresponding eigenvector.
Initialize the noise covariance matrix by,  .
.
Step 2.
Calculate  , and
, and  .
.  is the matrix of the
is the matrix of the  eigenvectors associated with the first
eigenvectors associated with the first  largest eigenvalues of
largest eigenvalues of  calculated at the first iteration.
calculated at the first iteration.  is the diagonal matrix containing the
is the diagonal matrix containing the  dominant eigenvalues.
dominant eigenvalues.
Let  .
.
Step 3.
Calculate the  element of the current noise covariance matrix
element of the current noise covariance matrix

Step 4.
Eigendecomposition of the matrix  . The new matrices
. The new matrices  and
and  are calculated using the previous steps. Repeat the algorithm until a significant improvement of the estimated noise covariance matrix is obtained.
are calculated using the previous steps. Repeat the algorithm until a significant improvement of the estimated noise covariance matrix is obtained.
Stop Test
The iteration is stopped when  or the Frobenius norm
or the Frobenius norm  calculated only with the elements such that
calculated only with the elements such that  for
for  and
and  is a fixed threshold. Symbol
is a fixed threshold. Symbol  stands for Frobenius norm and the superscript "
stands for Frobenius norm and the superscript " " indicates the
" indicates the  iteration.
iteration.
5.2. Estimation of the Spatial Correlation Length
In the previously proposed iterative algorithm, the spatial correlation length of the noise is supposed to be known. In practice, this is aforehand uncertain, therefore the search for a criterion of an estimate of  is necessary. In [21], one algorithm which jointly estimates the number of sources and the spatial correlation length of the noise is presented. We propose to vary the value of
is necessary. In [21], one algorithm which jointly estimates the number of sources and the spatial correlation length of the noise is presented. We propose to vary the value of  until the stability of the result is reached, that is, until the noise covariance matrix does not vary when
until the stability of the result is reached, that is, until the noise covariance matrix does not vary when  varies. The algorithm incorporating the choice of the correlation length
varies. The algorithm incorporating the choice of the correlation length  is presented in Figure 2. In the stop test, we check whether
is presented in Figure 2. In the stop test, we check whether  or not.
or not.
6. Simulation Results
In the following simulations, a uniform linear array of  omnidirectional sensors with equal interelement spacing
omnidirectional sensors with equal interelement spacing  is used, where
is used, where  is the mid-band frequency and
is the mid-band frequency and  is the velocity of propagation. The number of independent realizations used to estimate the covariance matrix of the received signals is
is the velocity of propagation. The number of independent realizations used to estimate the covariance matrix of the received signals is  . The signal sources are temporally stationary zero-mean white Gaussian processes with the same frequency
. The signal sources are temporally stationary zero-mean white Gaussian processes with the same frequency  . Three equipower uncorrelated sources impinge on the array, with the
. Three equipower uncorrelated sources impinge on the array, with the  . The noise power is taken as the average of the diagonal elements of the noise covariance matrix
. The noise power is taken as the average of the diagonal elements of the noise covariance matrix  .
.
To demonstrate the performance of the proposed algorithm, the following three situations are considered:
-
(i)
Band-Toeplitz noise covariance matrix, with each element given by a modeling function;
-
(ii)
Band-Toeplitz noise covariance matrix with the elements arbitrary chosen;
-
(iii)
Band noise covariance matrix used in [16].
In each case, two spatial correlation lengths are studied:  and
and  .
.
6.1. Noise Covariance Matrix Estimation and Results Obtained
To localize the directions of arrival of sources and to evaluate the performance of the proposed algorithm, the high-resolution methods such as MUSIC [9, 10] are used after the preprocessing, with priori knowledge of the exact number of sources ( ).
).
Example 1 (Band-Toeplitz noise covariance matrix).
In this example, the spatial correlation between the noises is exponentially decreasing along the antenna array and the elements of the noise covariance matrix are expressed as

where  is the noise variance equal for every sensor and
is the noise variance equal for every sensor and  is the spatial correlation coefficient. The values which are retained are,
is the spatial correlation coefficient. The values which are retained are,  and
and  .
.
In each of the two studied cases ( and
and  ), the noise covariance matrix is estimated with a fixed threshold value
), the noise covariance matrix is estimated with a fixed threshold value  after a few iterations and we notice that the number of iterations for
after a few iterations and we notice that the number of iterations for  is greater than that of
is greater than that of  .
.
Example 2 (Band-Toeplitz noise covariance matrix with the elements arbitrary chosen).
In this example, the covariance matrix elements are chosen such that their values are decreasing along the array of antenna. The noise covariance matrix has the same structure as in Example 1

-
(i)
The parameters used are in the case
 ,
,  ,
, 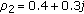 , and
, and  . Using the proposed algorithm, the three complex parameters of the noise covariance matrix can be perfectly estimated.
. Using the proposed algorithm, the three complex parameters of the noise covariance matrix can be perfectly estimated. -
(ii)
For
 :
:  ,
,  ,
,  ,
, 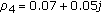 , and
, and  . The proposed algorithm gives good estimates of the simulated parameters.
. The proposed algorithm gives good estimates of the simulated parameters.
Example 3 (Band noise covariance matrix using model in [16, Example  ]).
]).
The configuration of this experiment contains a ten-element uniform rectilinear array with three sources at  ,
,  , and
, and  (angles are measured with respect to the normal of the array). One hundred snapshots of array data were taken.
(angles are measured with respect to the normal of the array). One hundred snapshots of array data were taken.
Example 3 o (typical correlated noise with sensor spacing  ).
).

where  is the noise variance equal for every sensor and
is the noise variance equal for every sensor and  is the spatial correlation coefficient. Figure 3 shows the root-mean-squared error versus sensor noise correlation factor
is the spatial correlation coefficient. Figure 3 shows the root-mean-squared error versus sensor noise correlation factor  over the range from 0 to 0.9. The SNR is held constant at
over the range from 0 to 0.9. The SNR is held constant at  , the number of sensor
, the number of sensor  and the noise spatial correlation length
and the noise spatial correlation length  .
.
Figure 4 presents the root-mean-squared error and the Cramer-Rao bound (CRB) [22] versus signal-to-noise ratio over the range from  to
to  dB.
dB.
Figure 5 shows the RMSE performances of the tested algorithms and the CRB with respect to the number of snapshots.
Figures 4 and 5 show that it is possible to mitigate the estimation error if SNR and/or the number of snapshots increase.
Example 3 t.
In order to study the influence of the estimation of the spatial correlation length on the localisation of the sources, we have considered the same data as in the previous example. The value of  is varied over the range 1 to
is varied over the range 1 to  and for each value the number of the sources (number of largest eigenvalues) is estimated after applying the proposed algorithm. Figure 6 shows that the estimation of the number of the sources is sensitive to the choice of
and for each value the number of the sources (number of largest eigenvalues) is estimated after applying the proposed algorithm. Figure 6 shows that the estimation of the number of the sources is sensitive to the choice of  . The number of the sources is correctly even the value of
. The number of the sources is correctly even the value of  is overestimated
is overestimated  . Figure 7 shows the variations of the bias of the estimated angles for different values of
. Figure 7 shows the variations of the bias of the estimated angles for different values of  . When
. When  is equal to 5 we obtain good results—
is equal to 5 we obtain good results— and very small value of a bias—this conclusion is observed for several scenarios.
and very small value of a bias—this conclusion is observed for several scenarios.
Figure 8 shows the norm of the vector difference between the 10 elements of the principal diagonal of the simulated matrix and those of the estimated matrix for  and
and  .
.
Comparing these results, we can remark that when  increases the estimation error increases. However, the estimation is still small.
increases the estimation error increases. However, the estimation is still small.
Figures 9(a), 9(b), 10(a), 10(b), 11(a), and 11(b) show the localization results of the sources before and after the preprocessing. Before the preprocessing, we use directly the MUSIC method to localize the sources. Once the noise covariance matrix is estimated with the proposed algorithm, this matrix is subtracted from the initial covariance matrix of the received signals, and then we use the MUSIC method to localize the sources. The three simulated sources are  ,
,  , and
, and  for Figure 9;
for Figure 9; ,
,  , and
, and  for Figure 10;
for Figure 10; ,
,  , and
, and  for Figure 11. For Figure 10, the SNR value (10 dB) is greater than those of Figures 9 and 11 (
for Figure 11. For Figure 10, the SNR value (10 dB) is greater than those of Figures 9 and 11 ( dB).
dB).
The comparison of the results of Figures 10 and 11 comes to the conclusion that the MUSIC method cannot separate the close sources without the preprocessing when the SNR is low, so in Figure 10 we can only detect two sources before preprocessing. And for each case we can note that there is an improvement in the results obtained with the preprocessing. Comparing the results of  with that of
with that of  for each figure, we can also reconfirm that when
for each figure, we can also reconfirm that when  increases, the estimation error increases on the estimated noise covariance matrix, so we obtain better results with the preprocessing for
increases, the estimation error increases on the estimated noise covariance matrix, so we obtain better results with the preprocessing for  than for
than for  .
.
RMSE versus sensor noise correlation: proposed method (solid) and MUSIC method in [ 16 ] (dashed).
In order to evaluate the performances of this algorithm, we study, below, the influence of the involved parameter  .
.
6.2. Performance of the Proposed Method versus Noise Spatial Correlation Length
Figure 12 shows the variations of the estimation error of the noise covariance matrix when the spatial correlation length of the noise  is increasing from
is increasing from  to
to  for two numbers of the sources
for two numbers of the sources  and
and  with
with  and
and  . This error is defined by,
. This error is defined by,  .
.
These results show that independently of the  -value the estimation error is null until
-value the estimation error is null until  and increases with
and increases with  value. This increasing estimation error is larger for greater values of
value. This increasing estimation error is larger for greater values of  .
.
To study the influence of  on the localization, we draw, see Figure 13, according to the spatial correlation length
on the localization, we draw, see Figure 13, according to the spatial correlation length  of the noise, the variations of the bias of estimate of the azimuths in the case of three sources localized at
of the noise, the variations of the bias of estimate of the azimuths in the case of three sources localized at  ,
,  and
and  .
.
We define that the bias of the  estimated directions of the arrival of the sources is calculated by
estimated directions of the arrival of the sources is calculated by

where

with the number of trials  .
.
The experimental results presented in Figure 13 show that the correlation length also influences the estimate of the DOA values.
The spatial correlation length  authorized by the algorithm is a function of the number of sensors and the number of sources. Indeed, the number of parameters of the signal to be estimated is
authorized by the algorithm is a function of the number of sensors and the number of sources. Indeed, the number of parameters of the signal to be estimated is  , and the number of parameters of the noise is
, and the number of parameters of the noise is  . In order to estimate them it is necessary that
. In order to estimate them it is necessary that  and that
and that  . In the limit case:
. In the limit case:  , we have
, we have  , which corresponds to a bidiagonal noise covariance matrix. If the model of the noise covariance matrix is band-Toeplitz [5, 21], the convergence of the proposed algorithm is fast, and the correlation length of the noise can reach
, which corresponds to a bidiagonal noise covariance matrix. If the model of the noise covariance matrix is band-Toeplitz [5, 21], the convergence of the proposed algorithm is fast, and the correlation length of the noise can reach  .
.
7. Experimental Data
The studied signals are recorded during an underwater acoustic experiment. The experiment is carried out in an acoustic tank under conditions which are similar to those in a marine environment. The bottom of the tank is filled with sand. The experimental device is presented in Figure 14(a). A source emits a narrow-band signal ( ). In addition to the signal source a spatially correlated Gaussian noise is emitted. The signal-to-noise ratio is
). In addition to the signal source a spatially correlated Gaussian noise is emitted. The signal-to-noise ratio is  . Our objective is to estimate the directions of arrival of the signals during the experiment. The signals are received on one uniform linear array. The observed signals come from various reflections on the objects being in the tank. Generally the aims of acousticians is the detection, localization and identification of these objects. In this experiment we have recorded the reflected signals by a single receiver. This receiver is moved along a straight line between position
. Our objective is to estimate the directions of arrival of the signals during the experiment. The signals are received on one uniform linear array. The observed signals come from various reflections on the objects being in the tank. Generally the aims of acousticians is the detection, localization and identification of these objects. In this experiment we have recorded the reflected signals by a single receiver. This receiver is moved along a straight line between position  and position
and position  with a step of
with a step of  in order to create a uniform linear array (see Figure 14(b)).
in order to create a uniform linear array (see Figure 14(b)).
Two objects are placed at the bottom of the tank and the emitting source describes a circular motion with a step of  by covering the angular band going from
by covering the angular band going from  to
to  . The signals received when the angle of emission is
. The signals received when the angle of emission is  are shown in Figure 15. This figure shows that there exists two paths, which may correspond to the reflected signals on the two objects. The results of the localization are given in Figure 16. We note that in spite of the presence of the correlated noise our algorithm estimate efficiently the DOA of the reflected signals during the experiment.
are shown in Figure 15. This figure shows that there exists two paths, which may correspond to the reflected signals on the two objects. The results of the localization are given in Figure 16. We note that in spite of the presence of the correlated noise our algorithm estimate efficiently the DOA of the reflected signals during the experiment.
Figure 16(a) shows the obtained results of the localization using MUSIC method on the covariance matrices. The DOA of the reflected signals on the two objects are not estimated. This is due to the fact that the noise is correlated.
Figure 16(b) shows the obtained results using our algorithm. The two objects are localized.
8. Conclusion
In this paper the problem of estimating the direction of arrival (DOA) of the sources in the presence of spatially correlated noise is studied. The spatial covariance matrix of the noise is modeled as a band matrix and is supposed to have a certain structure. In the numerical example, the noise covariance matrix is supposed to be the same for all sources, which covers many practical cases where the sources are enclosed.
This algorithm can be applied to the localization of the sources when the spatial-spectrum of the noise or the spatial correlation function between sensors is known. The obtained results show that the proposed algorithm improves the direction estimates compared to those given by the MUSIC algorithm without preprocessing. Several applications on synthetic data and experiment have been presented to show the limits of these estimators according to the signal-to-noise ratio, the spatial correlation length of the noise, the number of sources, and the number of sensors of the array. The motivation of this work is to reduce the effect of the additive spatially correlated noise for estimating the DOA of the sources.
References
Reilly JP, Wong KM: Estimation of the directions of arrival of signals in unknown correlated noise—II: asymptotic behavior and performance of the MAP approach. IEEE Transactions on Signal Processing 1992, 40(8):2018-2028. 10.1109/78.150003
Wu Q, Wong KM: UN-MUSIC and UNCLE: an application of generated correlation analysis to the estimation of direction-of-arrival of signals in unknown correlated noise. IEEE Transactions on Signal Processing 1994, 42(9):2331-2343. 10.1109/78.317855
Wax M: Detection and localization of multiple sources in noise with unknown covariance. IEEE Transactions on Signal Processing 1992, 40(1):245-249. 10.1109/78.157206
Ye H, DeGroat RD: Maximum likelihood DOA estimation and asymptotic Cramér-Rao bounds for additive unknown colored noise. IEEE Transactions on Signal Processing 1995, 43(4):938-949. 10.1109/78.376846
Chiao EC, Lorenzelli F, Hudson RE, Yao K: Stochastic maximum-likelihood DOA estimation in the presence of unknown nonuniform noise. IEEE Transactions on Signal Processing 2008, 56(7):3038-3044.
Le Cadre JP: Parametric methods for spatial signal processing in the presence of unknown colored noise fields. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(7):965-983. 10.1109/29.32275
Vorobyov SA, Gershman AB, Wong KM: Maximum likelihood direction-of-arrival estimation in unknown noise fields using sparse sensor arrays. IEEE Transactions on Signal Processing 2005, 53(1):34-43.
Zhang Y, Ye Z: Efficient method of DOA estimation for uncorrelated and coherent signals. IEEE Antennas and Wireless Propagation Letters 2008, 7: 799-802.
Tayem N, Kwon HM: Azimuth and elevation angle estimation with no failure and no eigen decomposition. Signal Processing 2006, 86(1):8-16. 10.1016/j.sigpro.2005.05.001
Cadzow JA: A high resolution direction-of-arrival algorithm for narrow-band coherent and incoherent sources. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(7):965-979. 10.1109/29.1618
Werner K, Jansson M: DOA estimation and detection in colored noise using additional noise-only data. IEEE Transactions on Signal Processing 2007, 55(11):5309-5322.
Friedlander B, Weiss AJ: Direction finding using noise covariance modeling. IEEE Transactions on Signal Processing 1995, 43(7):1557-1567. 10.1109/78.398717
Abeida H, Delmas J-P: Efficiency of subspace-based DOA estimators. Signal Processing 2007, 87(9):2075-2084. 10.1016/j.sigpro.2006.12.020
Stoica P, Viberg M, Ottersten B: Instrumental variable approach to array processing in spatially correlated noise fields. IEEE Transactions on Signal Processing 1994, 42(1):121-133. 10.1109/78.258127
Stoica P, Viberg M, Ottersten B, Kailath T: Optimal localization of partially known signals in unknown noise fields. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '94), 1994, Adelaide, Australia
Li F, Vaccaro RJ: Performance degradation of DOA estimators due to unknown noise fields. IEEE Transactions on Signal Processing 1992, 4(3):686-690.
Li M, Lu Y: Dimension reduction for array processing with robust interference cancellation. IEEE Transactions on Aerospace and Electronic Systems 2006, 42(1):103-112. 10.1109/TAES.2006.1603408
Viberg M: Sensitivity of parametric direction finding to colored noise fields and undermodeling. Signal Processing 1993, 34(2):207-222. 10.1016/0165-1684(93)90163-5
Gershman AB, Stoica P, Pesavento M, Larsson EG: Stochastic Cramér-Rao bound for direction estimation in unknown noise fields. IEE Proceedings: Radar, Sonar and Navigation 2002, 149(1):2-8. 10.1049/ip-rsn:20020124
Li M, Lu Y: Maximum likelihood DOA estimation in unknown colored noise fields. IEEE Transactions on Aerospace and Electronic Systems 2008, 44(3):1079-1090.
Nagesha V, Kay S: Maximum likelihood estimation for array processing in colored noise. IEEE Transactions on Signal Processing 1996, 44(2):169-180. 10.1109/78.485914
Hawkes M, Nehorai A: Acoustic vector-sensor correlations in ambient noise. IEEE Journal of Oceanic Engineering 2001, 26(3):337-347. 10.1109/48.946508
Acknowledgment
The authors would like to express their thanks to the anonymous reviewers for their careful reading and their helpful remarks, which have contributed in improving the clarity of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bourennane (EURASIPMember), S., Fossati, C. & Marot, J. Localization of Narrow-Band Sources in Unknown Spatially Correlated Noise. EURASIP J. Adv. Signal Process. 2010, 732591 (2010). https://doi.org/10.1155/2010/732591
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/732591





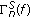 is diagonal.
is diagonal. , where
, where  are unknown parameters and
are unknown parameters and  are complex weighting matrices,
are complex weighting matrices, 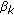 are chosen such that
are chosen such that 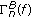 is positive definite and of band structure.
is positive definite and of band structure.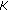 which means that the spatial correlation attains up to the
which means that the spatial correlation attains up to the 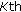 sensor;
sensor;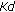 , where
, where  is the distance between sensors, are considered uncorrelated.
is the distance between sensors, are considered uncorrelated.
 sensors,
sensors,  is the noise spatial correlation coefficient.
is the noise spatial correlation coefficient.
 in the algorithm, where
in the algorithm, where  indicates the principal diagonal of the banded noise covariance matrix
indicates the principal diagonal of the banded noise covariance matrix  with spatial correlation length
with spatial correlation length  .
. ,
,  ,
, 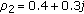 , and
, and  . Using the proposed algorithm, the three complex parameters of the noise covariance matrix can be perfectly estimated.
. Using the proposed algorithm, the three complex parameters of the noise covariance matrix can be perfectly estimated. :
:  ,
,  ,
,  ,
, 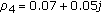 , and
, and  . The proposed algorithm gives good estimates of the simulated parameters.
. The proposed algorithm gives good estimates of the simulated parameters.

 : Cramer-Rao bound (stars) from [
: Cramer-Rao bound (stars) from [

 .
.
 .
.
 (solid) and for
(solid) and for
 (dashed).
(dashed).

 ,
,  , and
, and  without and with noise preprocessing for
without and with noise preprocessing for  and
and  .
.

 and
and  without and with noise preprocessing for
without and with noise preprocessing for  and
and  .
.

 and
and  without and with noise preprocessing for
without and with noise preprocessing for  and
and  .
.
 and
and  .
.


