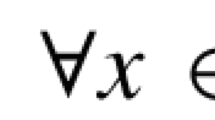Abstract
We establish a new Laypunov-type inequality for two nonlinear systems of partial differential equations and the discrete analogue is also established. As application, boundness of the two-dimensional Emden-Fowler-type equation is proved.
Similar content being viewed by others
1. Introduction
In a celebrated paper of 1893, Liapunov [1] proved the following well-known inequality: if 
is a nontrivial solution of
on an interval containing the points 
and b
such that 
then
Since the appearance of Liapunov's fundamental paper [1], considerable attention has been given to various extensions and improvements of the Lyapunov-type inequality from different viewpoints [2–7]. In particular, the Lyapunov-type inequalities for the following nonlinear system of differential equations were given in [8]
In this paper, we obtain new Lyapunov-type inequalities for the two-dimensional nonlinear system and discrete nonlinear system, respectively.
2. The Lyapunov-Type Integral Inequality for the Two-Dimensional Nonlinear System
We shall assume the existence of nontrivial solution 
of the system (2.1), and furthermore, (2.1) satisfies the following assumptions (i), (ii), and (iii):
(i)
, 
are real constants;
(ii)
, 
are continuous functions such that 
for 
;
(iii)
is a continuous function.
Theorem 2.1.
Let the hypotheses 
hold. If the nonlinear system (2.1) has a real solution 
such that 
for 
and 
and 
is not identically zero on 
, where 
with 
,
then
where 
, 
, and 
is the nonnegative part of 
Proof.
Since
and 
is not identically zero on 
, we can choose 
such that 
. Let 
. Integrating the first equation of system (2.1) over 
from 
to 
and over 
from 
to 
, respectively, we obtain
On the other hand, we have
Hence,
and similarly, we have
Employing the triangle inequality gives
Summing (2.7) and (2.8), we obtain
By using Hölder inequality on the second integral of the right side of (2.9) with indices 
and 
, we have
where 
.
Therefore, we obtain from (2.9)
On the other hand, we have
Multiplying the first equation of (2.1) by 
and the second one by 
, adding the result, and noting 
, we have
Integrating the left side of (2.13) over 
from 
to 
and over 
from 
to 
, respectively, we get
Now integrating both sides of (2.13) over 
from 
to 
and over 
from 
to 
, respectively, and noting 
we get
Substituting equality (2.15) by (2.11), we have
Noticing that 
and 
, we obtain
The proof is complete.
Remark 2.2.
Let 
change to 
in (2.2), and with suitable changes, (2.2) changes to the following result:
This is just a new Lyapunov-type inequality which was given by Tiryaki et al. [8].
3. The Lyapunov-Type Discrete Inequality for the Two-Dimensional Nonlinear System
where 
denotes the forward difference operator for 
that is, 
and 
denotes the forward difference operator for 
that is, 
We shall assume the existence of nontrivial solution 
of the system (3.1), and furthermore, (3.1) satisfies the following assumptions (
), (
), and (
):
(i)
are real constants;
(ii)
, 
are real-valued functions such that 
for all 
;
(iii)
is a real-valued function for all 
Theorem 3.1.
Let the hypotheses 
hold. Assume 
and 
If the nonlinear system (3.1) has a real solution 
such that 
for all 
and 
and 
is not identically zero on 
then
where 
, and 
Proof.
Let 
be nontrivial real solution of system (3.1) such that 
and 
is not identically zero on 
. Then multiplying the first equation of (3.1) by 
and the second one by 
adding the result, and noting 
and
we have
Summing the left side of (3.4) over 
from 
to 
and over 
from 
to 
, respectively, we have
Summing both sides of (3.4) over 
from 
to 
and over 
from 
to 
, respectively, and noting 
we obtain
Noticing that 
and 
we have
Choose 
such that 
Hence 
Summing the first equation of (3.1) over 
from 
to 
and over 
from 
to 
, respectively, we obtain
Considering the left side of (3.8) and noting 
for all 
we have
Hence,
and similarly, we have
Employing the triangle inequality gives
Summing (3.12) and (3.13), we obtain
On the other hand, using Hölder inequality on the second sum of the right side of (3.14) with indices 
and 
we have
where 
Therefore, from (3.7) and 
we obtain
Substituting (3.16) to (3.14), we have
Noticing that 
we get
This completes the proof.
Remark 3.2.
Let 
change to 
in (3.2) and with suitable changes, (3.2) changes to the following result:
This is just a new Lyapunov-type inequality which was given by Ünal et al. [2].
4. An application
Two-dimensional Emden-Fowler-type equation
where 
is a constant, 
and 
are real functions, and 
for all 
.
Consider the following special case of system (2.1), which is an equivalent system for the two-dimensional Emden-Fowler-type equation (4.1)
where 
and 
.
Obviously Theorem 2.1 for the two-dimensional nonlinear system (2.1) with 
is satisfied for system (4.2). Therefore, we have
A nontrivial solution 
of system (4.2) defined on 
is said to be proper if and only if
for any 
.A proper solution 
of system (4.2) is called weakly oscillatory if and only if at least one component has a sequence of zeros tending to 
.
Theorem 4.1.
If 
, where 
, 
and 
, 
is bounded on 
and 
is bounded on 
,
then every weakly oscillatory proper solution of (4.2) is bounded on 
.
Proof.
Let 
be any nontrivial weakly oscillatory proper solution of nonlinear system (4.2) on 
such that 
has a sequence of zeros tending to 
. Suppose to the contrary that 
; then given any positive number 
, we can find positive numbers 
and 
such that 
for all 
. Since 
is an oscillatory solution, there exist 
with 
such that 
and 
on 
. Choose 
in 
such that 
; in view of (4.5), we can choose 
and 
large enough such that for every 
, 
,
Taking 
th power of both sides of (4.3) and combining (4.6), we obtain
where 
and 
.
This contradiction shows that 
is bounded on 
. Therefore, there exists a positive constant 
such that 
for all 
.
On the other hand, integrating the second equation of system (4.2) over 
from 
to 
and over 
from 
to 
, respectively, we obtain
Notice that 
is bounded on 
, 
is bounded on 
, and in view of triangle inequality, we have
where 
is a constant.
Equation (4.9) implies that 
is bounded on 
since 
. It follows from
that 
is bounden on 
.
This completes the proof.
References
Liapunov AM: Probléme géneral de la stabilité du mouvement. Annales de la Faculté des Sciences de Toulouse 1907, 2: 27–247. French translation of a Russian paper dated 1893
Ünal M, Çakmak D, Tiryaki A: A discrete analogue of Lyapunov-type inequalities for nonlinear systems. Computers & Mathematics with Applications 2008, 55(11):2631–2642. 10.1016/j.camwa.2007.10.014
Ito H: A degree of flexibility in Lyapunov inequalities for establishing input-to-state stability of interconnected systems. Automatica 2008, 44(9):2340–2346. 10.1016/j.automatica.2008.01.001
Cañada A, Montero JA, Villegas S: Lyapunov inequalities for partial differential equations. Journal of Functional Analysis 2006, 237(1):176–193. 10.1016/j.jfa.2005.12.011
Jiang L, Zhou Z: Lyapunov inequality for linear Hamiltonian systems on time scales. Journal of Mathematical Analysis and Applications 2005, 310(2):579–593.
Guseinov GSh, Kaymakçalan B: Lyapunov inequalities for discrete linear Hamiltonian systems. Computers & Mathematics with Applications 2003, 45(6–9):1399–1416.
Pachpatte BG: Lyapunov type integral inequalities for certain differential equations. Georgian Mathematical Journal 1997, 4(2):139–148. 10.1023/A:1022930116838
Tiryaki A, Ünal M, Çakmak D: Lyapunov-type inequalities for nonlinear systems. Journal of Mathematical Analysis and Applications 2007, 332(1):497–511. 10.1016/j.jmaa.2006.10.010
Acknowledgments
This research is supported by National Natural Sciences Foundation of China (10971205). It is also partially supported by the Research Grants Council of the Hong Kong SAR, China (Project no. HKU7016/07P) and an HKU Seed Grant for Basic Research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, LY., Zhao, CJ. & Cheung, WS. On Lyapunov-Type Inequalities for Two-Dimensional Nonlinear Partial Systems. J Inequal Appl 2010, 504982 (2010). https://doi.org/10.1155/2010/504982
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/504982