Abstract
The paper addresses the algorithmic and architectural design of digital input power audio amplifiers. A modelling platform, based on a meet-in-the-middle approach between top-down and bottom-up design strategies, allows a fast but still accurate exploration of the mixed-signal design space. Different amplifier architectures are configured and compared to find optimal trade-offs among different cost-functions: low distortion, high efficiency, low circuit complexity and low sensitivity to parameter changes. A novel amplifier architecture is derived; its prototype implements digital processing IP macrocells (oversampler, interpolating filter, PWM cross-point deriver, noise shaper, multilevel PWM modulator, dead time compensator) on a single low-complexity FPGA while off-chip components are used only for the power output stage (LC filter and power MOS bridge); no heatsink is required. The resulting digital input amplifier features a power efficiency higher than 90% and a total harmonic distortion down to 0.13% at power levels of tens of Watts. Discussions towards the full-silicon integration of the mixed-signal amplifier in embedded devices, using BCD technology and targeting power levels of few Watts, are also reported.
Similar content being viewed by others
1. Introduction
Small size, low-cost and high-efficiency audio amplifiers, integrated as much as possible with digital audio signal processing tasks in the same embedded device, are required in several consumer applications: home and car entertainment, computer/portable multimedia players and, for low power levels, hearing aids devices. Conventional linear amplifiers feature low-distortion performance but have several disadvantages versus market needs [1, 2]: they are too heavy and energy inefficient and the achievable power density is limited by the physical size and cost of cooling hardware and power devices. An extra Digital-to-Analog Converter (DAC) is needed, before the analog amplifier, for digital sources: CD, Super Audio CD and DVD supports, MP3 files, and Digital Audio Broadcasting.
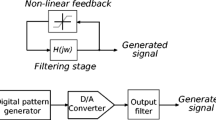
To achieve similar low-distortion performance of linear amplifiers but with a higher power efficiency, and hence smaller size and cost, the recent research has been focused on switching amplifiers. Several class D PWM (Pulse Width Modulation) topologies or hybrid class A–D or B–D ones have been proposed in literature [3–6]. However such topologies are still analog input amplifiers. An alternative solution is the direct amplification of the digital source based on the switching architecture at the bottom of Figure 1: in the digital domain the input PCM (Pulse Code Modulation) signal is directly converted in a PWM one; the latter is amplified by an inverter power bridge, switching at hundreds of kHz, and provided to the speaker after lowpass LC filtering.
1.1. The State of the Art of Digital Power Audio Amplifiers
A direct conversion of the input PCM stream to PWM is not useful: PWM is a nonlinear technique and the intermodulation between the PWM carrier frequency and the baseband audio signal leads to poor-quality amplifiers [7]. To this aim, in academia and industry [8–24], several techniques have been proposed to improve the basic scheme in Figure 1: new digital audio processing algorithms [12–15, 17–20, 22–24] or novel feedback schemes [9–11, 21] or multilevel PWM power bridges [16] have been published to correct the distortions introduced by the PWM modulation or by the nonideal behaviour of the power stage. However the new proposed techniques require extra hardware resources; the performance gain is paid in terms of increased circuital complexity and cost. The overall amplifier often requires multiple chips for the digital part (including digital signal processor and/or ASIC and/or FPGA), plus ADC and high-order analog filters for the feedback plus multiple power transistors and gate drivers for multi level PWM. As a result high-performance systems require high circuit complexity, implemented using multiple chips and often multiple-boards, and are not suitable for consumer applications or embedded devices. Solutions with lower complexity are usually obtained at the expense of audio quality reduction.
1.2. Aim and Outline of This Work
This work explores the design space of digital audio amplifiers to find an optimal mixing of different analog and digital techniques. The resulting architecture aims at achieving optimal performance in terms of low-distortion and high power efficiency while still allowing a low-cost implementation: all the digital processing part integrated in a single device, for example, a low-complexity FPGA, plus off-chip components only for the power stage, made up of a MOS H-bridge and an LC filter but without any heat sink.
Most state-of-the-art techniques propose specific optimizations for just a part of the scheme in Figure 1; when integrating together different known techniques the relevant hardware overheads add up while the extra gain in performance can be negligible. However, the exhaustive design space exploration of digital power audio amplifiers is not straightforward since it needs fast but still accurate models involving the codesign of heterogeneous components: computation intensive processing algorithms at functional level with hardware components at physical level; low power digital and mixed-signal circuits with analog power devices; silicon integrated circuits with discrete devices. Hereafter Section 2 presents a platform-based modelling flow and the cost metrics used to drive the design space analysis. The models used to find optimal trade-offs between complexity, power efficiency, distortion and sensitivity are presented in Section 3 together with architectural comparison results. Section 4 shows the prototyping of the selected architecture targeting power levels of tens of Watts. Section 5 compares the obtained results versus the state of the art and discusses the extension of the work to fully integrated amplifiers for power levels of few Watts. Conclusions are drawn in Section 6.
2. Platform-Based Design Flow and Metrics
2.1. Design Metrics Definition
The definition of the multiple cost metrics to be optimized is essential to drive the design space exploration and the correct comparison of different architectures. The design metrics are the audio signal distortion, the power efficiency, the circuit complexity and the architecture sensitivity to parameter changes. The input signals are PCM samples with a bit size n from 16 to 24 and a sample frequency  between 44 kS/s and 96 kS/s (the lower values for frequency and bit-size are typical of audio CD while the higher values are used in audio DVD). The target output power, Pout, amounts to tens of Watts with power efficiency levels up to 90%. Reported data in this paper refer to the example case of max Pout of 70 Wrms (or 35 Wrms) delivered to a 4
between 44 kS/s and 96 kS/s (the lower values for frequency and bit-size are typical of audio CD while the higher values are used in audio DVD). The target output power, Pout, amounts to tens of Watts with power efficiency levels up to 90%. Reported data in this paper refer to the example case of max Pout of 70 Wrms (or 35 Wrms) delivered to a 4  (or 8
(or 8  ) speaker. The total harmonic distortion (THD) considered for High-Fidelity (Hi-Fi) is a level lower than 0.2%, the optimal target is 0.1%. As discussed in [1] there are high-end products for professional applications, using linear amplifiers, with THD figures below 0.001%; however the subjective sensitivity of the hearing human system to THD levels below 0.3% is often negligible. Most Hi-Fi amplifiers, for example, Sony STR-DE445 [13], for consumer home or car markets have a THD of 0.2%. The considered frequency response in this paper is 20 Hz–20 kHz, although THD optimizations focus on the range 500 Hz to 2 kHz where the hearing human system is mainly sensible and very often music signals are below 16-17 kHz [1]. The target circuit complexity for the digital processing circuitry amounts to tens of equivalent ASIC gates, a value that can be fitted in a single low-cost FPGA leaving space to integrate other audio processing tasks thus realizing a complete audio acquisition/playing system in a single embedded device.
) speaker. The total harmonic distortion (THD) considered for High-Fidelity (Hi-Fi) is a level lower than 0.2%, the optimal target is 0.1%. As discussed in [1] there are high-end products for professional applications, using linear amplifiers, with THD figures below 0.001%; however the subjective sensitivity of the hearing human system to THD levels below 0.3% is often negligible. Most Hi-Fi amplifiers, for example, Sony STR-DE445 [13], for consumer home or car markets have a THD of 0.2%. The considered frequency response in this paper is 20 Hz–20 kHz, although THD optimizations focus on the range 500 Hz to 2 kHz where the hearing human system is mainly sensible and very often music signals are below 16-17 kHz [1]. The target circuit complexity for the digital processing circuitry amounts to tens of equivalent ASIC gates, a value that can be fitted in a single low-cost FPGA leaving space to integrate other audio processing tasks thus realizing a complete audio acquisition/playing system in a single embedded device.
2.2. Platform-Based Design Flow
To allow a fast but still accurate design space exploration we followed a meet-in-the-middle approach between bottom-up and top-down strategies [25]. A configurable modelling platform has been built starting from libraries of analog and digital building block components. A library of accurate spice models has been derived bottom-up for the hardware components whose nonideal characteristics and nonlinearity affect the behaviour of the power audio amplifier: power MOS, power supply, analog filters, OpAmp and comparators optionally used in the feedback loop. As example, we have created Spice models for the power MOS in [26], used also in the prototyping phase; such models consider all key electrical parameters [27] and their dependence on input driving signal ( ) and output delivered power: MOS transfer curves, drain source breakdown voltage
) and output delivered power: MOS transfer curves, drain source breakdown voltage  ,
,  on resistance, gate charge
on resistance, gate charge  , body diode reverse recovery charge
, body diode reverse recovery charge  , internal gate resistance
, internal gate resistance  , MOS rise and fall times
, MOS rise and fall times  and
and  and switching frequency
and switching frequency  , transistor packaging and thermal characteristics. The Spice models have been integrated with parametric and fixed-point Simulink models for the signal processing algorithms proposed to enhance the basic scheme in Figure 1, see details in Section 3. The resulting Spice/Simulink environment is then used top-down to build multiple architectures (proper configuring and combining the building block models) and to allow their fast but still accurate comparison. The considered design metrics are those in Section 2.1. This analysis allows a first selection of the most promising architectures; for them the comparison is further refined in a second step using HDL models for the digital audio algorithms.
, transistor packaging and thermal characteristics. The Spice models have been integrated with parametric and fixed-point Simulink models for the signal processing algorithms proposed to enhance the basic scheme in Figure 1, see details in Section 3. The resulting Spice/Simulink environment is then used top-down to build multiple architectures (proper configuring and combining the building block models) and to allow their fast but still accurate comparison. The considered design metrics are those in Section 2.1. This analysis allows a first selection of the most promising architectures; for them the comparison is further refined in a second step using HDL models for the digital audio algorithms.
Synthesized on different technologies (standard-cells CMOS libraries or SRAM-based FPGAs) the HDL models permit the evaluation of the gate complexity and power consumption of the digital circuitry. The selected architectures are finally prototyped, and the real performances measured, using FPGA technology plus a discrete power output stage.
3. Mixed-Signal Architectural Exploration
This section presents the modelling platform which includes the following building blocks, see Figure 2: an over sampler, a cross point estimator for natural PWM, a sigma-delta noise shaper, a multilevel PWM generator, a dead time insertion unit, a power bridge, an LC filtering stage, a feedback loop with PWM signal compensation. To each building block parametric functional and cost models have been associated. For some blocks multiple algorithms are implemented. By combining the different building blocks and configuring their parameters, different possible architectures have been obtained, simulated and compared. The following subsections detail the architectures and functionalities implemented in each block of Figure 2, the relevant parameters, and the results obtained from the comparison of different configurations. The most suited choices for block combination and parameter configuration are also highlighted.
3.1. Oversampler
To reduce the output THD an oversampler is added before the PCM to PWM conversion in the digital domain, see Figure 2. Oversampling by a parametric factor M is realized first inserting M-1 zeros after each original sample (zero padding); the data stream is then processed with an interpolating filter to remove high frequency spurious repetitions of the baseband signal. The higher the oversampling factor M is, the higher ( ) the PWM carrier frequency is and hence the transition bandwidth for the LC output filter used to remove intermodulation distortion. Thus, a high over-sampling factor M simplifies the design of the LC analog filter at the expense of an increased complexity for the digital interpolating filter.
) the PWM carrier frequency is and hence the transition bandwidth for the LC output filter used to remove intermodulation distortion. Thus, a high over-sampling factor M simplifies the design of the LC analog filter at the expense of an increased complexity for the digital interpolating filter.
During simulations to find the most suited sizing for the factor M and for the oversampling filter structure, the masks in Table 1 have been used to specify the filter magnitude response. Mask 1 is known in literature [28, 29] while mask 2 is a new proposal of this work. Compared to mask 1, mask 2 features more stringent requirements in terms of pass-band ripple and stop-band attenuation (needed to meet a target THD  0.2%) but allows for a larger transition band; indeed music signals rarely exceed the 17 kHz imposed by a pass-band of 0.4
0.2%) but allows for a larger transition band; indeed music signals rarely exceed the 17 kHz imposed by a pass-band of 0.4  and hence the pass-band 0.45
and hence the pass-band 0.45  in mask 1 is often excessive.
in mask 1 is often excessive.
Once specified the magnitude response of the filter it is important to define its architectural implementation (FIR or IIR, windowing type, direct or cascade multistage structure, parallel or iterative implementation of the multiply and accumulate-MAC- unit, data bit width), since its hardware cost can represent the main bottleneck of the whole audio system [28–32].
For the audio interpolating filter an FIR approach has to be preferred to an IIR for its linear phase response. However to implement the masks in Table 1 with an oversampling factor  a direct implementation of an FIR type needs a number of taps, that is, a filter order Z, of some hundreds as reported in Table 2. Equiripple and Kaiser FIR types are considered in Table 2; analysis carried out using Gaussian, Hamming and Hanning FIR windows lead to similar results of the Kaiser FIR type. Such high filter orders entail a high computational complexity which amounts to roughly
a direct implementation of an FIR type needs a number of taps, that is, a filter order Z, of some hundreds as reported in Table 2. Equiripple and Kaiser FIR types are considered in Table 2; analysis carried out using Gaussian, Hamming and Hanning FIR windows lead to similar results of the Kaiser FIR type. Such high filter orders entail a high computational complexity which amounts to roughly  MAC operations per sample. On the contrary using an IIR structure the same magnitude response can be obtained with a much lower filter order: see Table 2 which considers Butterworth, Chebychev and elliptic IIR filters.
MAC operations per sample. On the contrary using an IIR structure the same magnitude response can be obtained with a much lower filter order: see Table 2 which considers Butterworth, Chebychev and elliptic IIR filters.
The filter computational burden further increases when considering oversampling factors M much higher than 8. As example Table 3 reports the PWM carrier frequency  , the filter order and the MAC operations needed for Equiripple and Kaiser FIR filters when varying the oversampling factor from 8 to 128 with CD-quality
, the filter order and the MAC operations needed for Equiripple and Kaiser FIR filters when varying the oversampling factor from 8 to 128 with CD-quality  kS/s.
kS/s.
From Table 3 it is clear that (i) the computational cost of a direct FIR implementation amounts to tens of millions MAC/s for  and becomes prohibitive, in the range of tens of Giga MAC/s, when M grows up to 128; (ii) considering off-chip power output bridges (see Section 3.6) with typical PWM frequencies within 1 MHz, oversampling factors M higher than 8 or 16 should be avoided.
and becomes prohibitive, in the range of tens of Giga MAC/s, when M grows up to 128; (ii) considering off-chip power output bridges (see Section 3.6) with typical PWM frequencies within 1 MHz, oversampling factors M higher than 8 or 16 should be avoided.
To reduce the computational cost of FIR filters while keeping the advantages of their better phase response versus IIR structures, the following solutions can be adopted [29].
-
(1)
Polyphase filter implementation: in the oversampling unit
 -1 samples out of M are zeros (due to zero padding) and hence a polyphase structure reduces the required MAC operations for the interpolating filter by a factor M.
-1 samples out of M are zeros (due to zero padding) and hence a polyphase structure reduces the required MAC operations for the interpolating filter by a factor M. -
(2)
Multistage cascade realization: the oversampling unit can be realized through a cascade of S multiple stages where the i th stage realizes an oversampling by a factor Mi (with
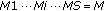 ) with a filter of reduced order
) with a filter of reduced order 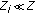 .
.
Table 4 shows the overall MAC computational cost, considering polyphase filter implementations, of different possible partitioning of the whole oversampling unit in multiple cascaded stages. The analysis in Table 4 considers an oversampling factor  or 16 and
or 16 and  kS/s. In case of DVD-audio with
kS/s. In case of DVD-audio with  kS/s, MAC computations and PWM frequency in Tables 3 and 4 are doubled.
kS/s, MAC computations and PWM frequency in Tables 3 and 4 are doubled.
Comparing the results of Tables 3 and 4 it is clear that, exploiting the multistage decomposition and the poly-phase techniques, the filter complexity is reduced to few millions of MAC/s.
The computational burden in Table 4 is roughly the same for the two mask types; in the rest of the work mask 2 is used since it ensures a lower pass-band ripple. Using the Equiripple filter type a computational saving of roughly 30% is achieved versus the Kaiser type.
By adopting an oversampling factor  , 4-stage polyphase FIR filter of Equiripple type with filter mask 2, the required complexity can be sustained for both CD-quality and DVD-quality inputs realizing in hardware a single MAC unit with 1 MAC/cycle capability and with a clock frequency below 10 MHz. The use of higher oversampling factors is still limited by the switching frequency of the power output bridge (see Section 3.6).
, 4-stage polyphase FIR filter of Equiripple type with filter mask 2, the required complexity can be sustained for both CD-quality and DVD-quality inputs realizing in hardware a single MAC unit with 1 MAC/cycle capability and with a clock frequency below 10 MHz. The use of higher oversampling factors is still limited by the switching frequency of the power output bridge (see Section 3.6).
Finally, the bit-true arithmetic of the MAC hardware unit has been determined: using a 12-bit fixed-point data width the circuit complexity is greatly reduced versus a floating—point arithmetic implementation while the reduction of audio reproduction quality is negligible.
3.2. Noise Shaper
Converting the n-bit oversampled PCM signal to PWM leads to a minimum impulse time  , for example, roughly 0.25 nanoseconds considering
, for example, roughly 0.25 nanoseconds considering  and the 44.1 kS/s 16-bit PCM signal of audio CDs. Such values are too low for commercial power transistors [26, 27] with rise and fall times, T
r
and T
f
, of tens of nanoseconds. To reduce such requirement while keeping unaltered source audio quality, a noise shaper is used. Its architecture is shown in Figure 3: it reduces the used bits from n to p, while the added quantization noise can be spread outside the audio band using a
and the 44.1 kS/s 16-bit PCM signal of audio CDs. Such values are too low for commercial power transistors [26, 27] with rise and fall times, T
r
and T
f
, of tens of nanoseconds. To reduce such requirement while keeping unaltered source audio quality, a noise shaper is used. Its architecture is shown in Figure 3: it reduces the used bits from n to p, while the added quantization noise can be spread outside the audio band using a  order FIR shaping filter. In our model the noise shaper is parametric in terms of output bit width p and filter order K. An high value for K leads to improved SNR performances but also to an increased circuit complexity and to the risk of loop instability. Our analysis proves that stable loops and good trade-offs between audio performance and circuit complexity can be achieved using p between 4 and 8 bits and noise shapers with an FIR filter up to
order FIR shaping filter. In our model the noise shaper is parametric in terms of output bit width p and filter order K. An high value for K leads to improved SNR performances but also to an increased circuit complexity and to the risk of loop instability. Our analysis proves that stable loops and good trade-offs between audio performance and circuit complexity can be achieved using p between 4 and 8 bits and noise shapers with an FIR filter up to  order. Figure 4 reports the magnitude response of the selected noise shaping filter for the prototyping phase described in Section 4. The noise shaper transfer function NTF is
order. Figure 4 reports the magnitude response of the selected noise shaping filter for the prototyping phase described in Section 4. The noise shaper transfer function NTF is  , being
, being  the shaping filter response.
the shaping filter response.
The most suited values for M and p depend on the time response of the used power MOS; the minimum impulse time  should be comparable to the sum of T
r
and T
f
. As example for CD-audio signals, using
should be comparable to the sum of T
r
and T
f
. As example for CD-audio signals, using  ,
,  leads to a
leads to a  of 11 nanoseconds compatible with the timing of the selected power MOS devices [26].
of 11 nanoseconds compatible with the timing of the selected power MOS devices [26].
3.3. Cross Point Estimator for NPWM
The scheme with oversampling plus noise shaping implements the Uniform sampled PWM (UPWM). To further reduce the THD a Natural PWM (NPWM) modulation can be realized. For NPWM, see Figures 2 and 5, a cross-point deriver is added after the oversampling unit to estimate the intersection point between the sawtooth carrier and the original modulating signal as in analog PWM. In our mixed-signal model we have implemented four cross point estimators with different performance-complexity trade-offs. Two high-performance algorithms to estimate the NPWM cross point have been derived from [22], based on the iterative application of a Newton-Rapson method, and from [13], based on a 4-point Lagrange interpolator. Our simulations prove that these cross point estimators can reduce the THD down to 0.02% but at the expense of high computational cost. Hundreds of millions of MAC operations per second are required for CD inputs and hence an extra DSP processor has to be dedicated to the cross-point estimation task.
Simplified 2-point estimators for NPWM, using linear interpolation (LI) or delta compensation ( ), allow a single chip implementation of the whole signal processing part. Here the crossing-point is estimated using the first-order formulas reported in Figure 5 requiring just 1 multiply/sample for
), allow a single chip implementation of the whole signal processing part. Here the crossing-point is estimated using the first-order formulas reported in Figure 5 requiring just 1 multiply/sample for  and 1 division/sample for LI. Differently from [14, 15], where LI is preferred to
and 1 division/sample for LI. Differently from [14, 15], where LI is preferred to  in case of micropower speech amplifiers not using oversampling, our simulations prove that the THD reduction using NPWM-LI or -
in case of micropower speech amplifiers not using oversampling, our simulations prove that the THD reduction using NPWM-LI or - is the same: a factor of 2 lower than UPWM. Thus, the use of
is the same: a factor of 2 lower than UPWM. Thus, the use of  C is preferred since it is less complex than LI requiring the computation of a multiplication/sample instead of a division/sample.
C is preferred since it is less complex than LI requiring the computation of a multiplication/sample instead of a division/sample.
3.4. Multilevel PWM
A classic PWM has  levels but also
levels but also  levels PWM and
levels PWM and  PWM techniques, up to 9 in [16], can be implemented. In 2-state PWM the signal is switching between maximum and minimum supply voltage values, the two states
PWM techniques, up to 9 in [16], can be implemented. In 2-state PWM the signal is switching between maximum and minimum supply voltage values, the two states  and
and  . Even for low-level signals binary modulation continuously provides energy to the LC filter and to the load. If the modulating input is null the PWM wave is still switching with a 50% duty cycle. The signal provided to the load is null but switching losses are paid thus reducing power efficiency. The 3-state PWM signal switches between
. Even for low-level signals binary modulation continuously provides energy to the LC filter and to the load. If the modulating input is null the PWM wave is still switching with a 50% duty cycle. The signal provided to the load is null but switching losses are paid thus reducing power efficiency. The 3-state PWM signal switches between  and 0 when the input signal is positive, otherwise between
and 0 when the input signal is positive, otherwise between  and 0. In case of null input there is no switching activity and hence switching losses are reduced. The 3-state PWM modulator reduces by a factor 2 the voltage swing supported by the power MOS transistors allowing also the reduction of electromagnetic interference (EMI) and a better behaviour of the power devices. By further increasing the number of levels L the EMI and the switching losses can be further reduced. However while 2 and 3 levels PWM can be implemented with a single power MOS bridge, a PWM with levels
and 0. In case of null input there is no switching activity and hence switching losses are reduced. The 3-state PWM modulator reduces by a factor 2 the voltage swing supported by the power MOS transistors allowing also the reduction of electromagnetic interference (EMI) and a better behaviour of the power devices. By further increasing the number of levels L the EMI and the switching losses can be further reduced. However while 2 and 3 levels PWM can be implemented with a single power MOS bridge, a PWM with levels  require multiple power bridges, with matched behaviour. This increases remarkably the amplifier complexity and cost. Our analysis proves that for
require multiple power bridges, with matched behaviour. This increases remarkably the amplifier complexity and cost. Our analysis proves that for  the complexity increase is not justified by a performance gain which is limited if compared to ternary PWM.
the complexity increase is not justified by a performance gain which is limited if compared to ternary PWM.
While the power output stage can be the same for 2 and 3 levels PWM, the digital circuitry is different. To generate a 2-state PWM digital wave each p-bit noise shaped and oversampled sample is compared to a digital sawtooth waveform. The 3-state PWM modulator is realized using two 2-state PWM modulators, one for positive input samples and the other for negative samples: after controlling the sign of each sample only one of the two 2-state modulators is enabled. Although 3-state PWM modulation doubles the cost of the 2-state one the complexity of the whole system is comparable. Indeed, as shown in Section 4, the overall digital circuitry complexity is dominated by the noise shaping and oversampling filters which are common to 3- and 2-state PWM. Summarizing 3 levels PWM is the best trade-off between performance and circuit complexity.
3.5. Dead Time Insertion
Before driving the power stage, proper guard intervals have to be inserted at the beginning and at the end of each PWM word to take into account the switching delay time of the selected power MOS devices. The minimal time resolution of the PWM wave is  , determined by the oversampling and noise shaping choices, which can be smaller than the switching transition time of typical power MOS. As example the sizing in Section 3.2 leads to a
, determined by the oversampling and noise shaping choices, which can be smaller than the switching transition time of typical power MOS. As example the sizing in Section 3.2 leads to a  of 11 nanoseconds smaller than the 20 nanoseconds switching delay of the selected MOS devices [26]. If the time guard intervals are not inserted, PWM words with duty cycles of few % or near 100%, that is, with high or low time intervals of tens of nanoseconds, cannot be correctly managed by the power stage and distortions will arise. Moreover, since the switching times of P- and N- MOS are not the same, for each transition of the PWM signal there is the risk of a short circuit between the voltage supplies (a MOS is already on while the other is not completely off). To avoid these power wasting phenomena extra dead time intervals have to be inserted when the PWM wave is switching. On the other hand the higher the inserted time guard and dead time intervals, the higher the reduction of the amplifier dynamic range. An optimal sizing of the time intervals to be inserted can be found simulating in the Simulink/Spice environment the whole amplifier including accurate models of the power MOS time response. Figure 6 shows the THD reduction factor, that is, the ratio between the THD obtained when inserting different guard intervals tg versus the THD obtained without any time guard. In Figure 6 the THD is reduced up to a factor 4 using a tg of 30 nanoseconds (curve "typical"). The example architecture considered in Figure 6 is that with oversampling and noise shaping sized as in Section 3.2 plus ternary PWM, power stage of Section 3.6, no feedback loop. The optimal value for tg in Figure 6 is derived from architecture simulations; a mathematical formula in closed form is not available. When considering PVT (process, voltage and temperature) variations of the implementing hardware devices (e.g., the FPGA and the power components of the prototype in Section 4) the THD reduction curve varies; see as example in Figure 6 the curves reported with dashed lines corresponding to the "min" and "max" corner cases. Using the tg value calculated in nominal conditions (30 nanoseconds in our case, see "typ" curve in Figure 6) a suboptimal, but still noticeable, THD improving factor is obtained versus the case with no time guard insertion. In Figure 6 with tg = 30 nanoseconds the THD reduction versus the case without any time guard is from 0.25 to 0.55 depending on the PVT conditions. Moreover, as discussed in Section 3.5, the use of a proper feedback scheme can reduce the architecture sensitivity to parameters variation.
of 11 nanoseconds smaller than the 20 nanoseconds switching delay of the selected MOS devices [26]. If the time guard intervals are not inserted, PWM words with duty cycles of few % or near 100%, that is, with high or low time intervals of tens of nanoseconds, cannot be correctly managed by the power stage and distortions will arise. Moreover, since the switching times of P- and N- MOS are not the same, for each transition of the PWM signal there is the risk of a short circuit between the voltage supplies (a MOS is already on while the other is not completely off). To avoid these power wasting phenomena extra dead time intervals have to be inserted when the PWM wave is switching. On the other hand the higher the inserted time guard and dead time intervals, the higher the reduction of the amplifier dynamic range. An optimal sizing of the time intervals to be inserted can be found simulating in the Simulink/Spice environment the whole amplifier including accurate models of the power MOS time response. Figure 6 shows the THD reduction factor, that is, the ratio between the THD obtained when inserting different guard intervals tg versus the THD obtained without any time guard. In Figure 6 the THD is reduced up to a factor 4 using a tg of 30 nanoseconds (curve "typical"). The example architecture considered in Figure 6 is that with oversampling and noise shaping sized as in Section 3.2 plus ternary PWM, power stage of Section 3.6, no feedback loop. The optimal value for tg in Figure 6 is derived from architecture simulations; a mathematical formula in closed form is not available. When considering PVT (process, voltage and temperature) variations of the implementing hardware devices (e.g., the FPGA and the power components of the prototype in Section 4) the THD reduction curve varies; see as example in Figure 6 the curves reported with dashed lines corresponding to the "min" and "max" corner cases. Using the tg value calculated in nominal conditions (30 nanoseconds in our case, see "typ" curve in Figure 6) a suboptimal, but still noticeable, THD improving factor is obtained versus the case with no time guard insertion. In Figure 6 with tg = 30 nanoseconds the THD reduction versus the case without any time guard is from 0.25 to 0.55 depending on the PVT conditions. Moreover, as discussed in Section 3.5, the use of a proper feedback scheme can reduce the architecture sensitivity to parameters variation.
3.6. Output Power Stage
Figure 7 reports the circuit schematic of the full bridge power stage, using commercial power MOS from [26]. A complementary N-/P-MOS solution is adopted. A level-shifting circuitry is used for high-side gate driving. Discrete power MOS are available with associated gate driver buffers (represented by B1, B2, B3, B4 in Figure 7), allowing the connection of the output power stage to the PWM output of a low-power digital circuit, such as an FPGA. For the target power levels of this work the supply voltage Vdd in Figure 7 is sized at 25 V. The LC filter in Figure 7 is a differential 4th-order Butterworth with 20 kHz cutoff. In our model we compared several LC filtering stages, with different filter order and considering Butterworth, Chebychev and Elliptic types. Figure 8 reports the THD achieved using Butterworth, Chebychev (0.5 dB pass-band ripple) and Elliptic (0.1 dB pass-band ripple) analog filters with a cutoff frequency of 20 kHz and considering different filter orders. From Figure 8 it can be noted that the performances of the filters are similar (elliptic filters are not defined for orders lower than 3). Butterworth type is preferred to avoid ripple in the pass-band. After the 4th order the THD reduction obtained increasing the filter complexity is minor.
3.7. Feedback Topologies
As far as feedback topology is concerned different schemes have been modelled. One solution is an open loop amplifier avoiding the problem of how to reinsert the power output signal in the low-power digital processing chain. This solution is widely adopted in literature, for example, in [13, 19]. Our simulations prove that an open loop scheme adopting oversampling, noise shaping,  C cross point estimation, 3-level PWM and dead time compensation (this scheme is nicknamed A1 in Figures 9 and 10) can be properly configured taking into account the real characteristics of the power stage. This open-loop amplifier leads to optimal THD and power efficiency results, see Figures 9 and 10, comparable to those obtained with closed-loop feedback amplifiers but avoiding extra hardware components. However if a circuit parameter changes (e.g., the PVT variations discussed in Section 3.4 and Figure 6) versus the reference value used for configuration or the supply voltage is affected by ripple there is not a compensating mechanism. Indeed, for open loop amplifiers it is mandatory the use of regulated supply voltages [19]. To reduce the amplifier sensitivity a feedback loop can be added to the architecture configuration A1. As example, in the architecture nicknamed A2 in Figures 9 and 10, the signal generated by the digital PWM modulator is compared to a scaled version of the output amplified PWM wave. Their difference Verr is sent to a lowpass analog controller, with transfer function C(s), extracting the DC component of the error. In our model we considered and simulated for C(s) an active filter (OpAmp plus RC network) with parametric cutoff frequency and filter order. The generated DC error level is then used in the PWM correction unit of Figure 2 to properly insert time delays in the PWM modulator thus driving the power MOS stage with a corrected PWM signal. Note that such approach is similar to some feedback algorithms proposed in literature: for example, in [9] C(s) is realized as a simple
C cross point estimation, 3-level PWM and dead time compensation (this scheme is nicknamed A1 in Figures 9 and 10) can be properly configured taking into account the real characteristics of the power stage. This open-loop amplifier leads to optimal THD and power efficiency results, see Figures 9 and 10, comparable to those obtained with closed-loop feedback amplifiers but avoiding extra hardware components. However if a circuit parameter changes (e.g., the PVT variations discussed in Section 3.4 and Figure 6) versus the reference value used for configuration or the supply voltage is affected by ripple there is not a compensating mechanism. Indeed, for open loop amplifiers it is mandatory the use of regulated supply voltages [19]. To reduce the amplifier sensitivity a feedback loop can be added to the architecture configuration A1. As example, in the architecture nicknamed A2 in Figures 9 and 10, the signal generated by the digital PWM modulator is compared to a scaled version of the output amplified PWM wave. Their difference Verr is sent to a lowpass analog controller, with transfer function C(s), extracting the DC component of the error. In our model we considered and simulated for C(s) an active filter (OpAmp plus RC network) with parametric cutoff frequency and filter order. The generated DC error level is then used in the PWM correction unit of Figure 2 to properly insert time delays in the PWM modulator thus driving the power MOS stage with a corrected PWM signal. Note that such approach is similar to some feedback algorithms proposed in literature: for example, in [9] C(s) is realized as a simple  order integrator while in [11] a more performing algorithm called PEDEC (Pulse Edge Delay Error Control) is used for PWM correction, starting from the generated DC error level. The results in Figures 9 and 10 for the amplifier nicknamed A2 refer to a feedback configuration with a
order integrator while in [11] a more performing algorithm called PEDEC (Pulse Edge Delay Error Control) is used for PWM correction, starting from the generated DC error level. The results in Figures 9 and 10 for the amplifier nicknamed A2 refer to a feedback configuration with a  order lowpass C(s) filter and using PEDEC as compensating technique. This approach provides good results but is not useful for a low-complexity and low-cost realization since it requires an extra analog feedback network.
order lowpass C(s) filter and using PEDEC as compensating technique. This approach provides good results but is not useful for a low-complexity and low-cost realization since it requires an extra analog feedback network.
With respect to that adopted in A2, more complex mixed-signal feedback correction schemes have been proposed in literature [10, 18]. In these schemes the output PWM power signal, after attenuation and filtering, is converted in the digital domain through extra ADCs: 7-bit flash ADC in [10] and 10-bit SAR ADC in [18]. In the digital domain similar operations to those of A2 are carried out. These feedback schemes using ADC and operating in the digital domain have been also modelled. The achievable THD and sensitivity performances are slightly better than those of A2 while the hardware overhead is much higher: an attenuator, a filter and an ADC are required in the analog domain plus a digital correcting unit in the digital one. Being too complex the feedbacks schemes with ADCs are not considered in the comparison of Figures 9 and 10.
A simpler but effective feedback correction technique to reduce the amplifier sensitivity to parameter changes is derived from [21]: the sign of the output current provided to the load is used as 1-bit control to check periodically which output transistor is on and to change consequently the inserted time-guard value. In [21] this technique has been proposed for the control of a 2-state PWM power-bridge. In this work this approach has been redesigned to be integrated with oversampling, noise shaping,  C cross point estimation and 3-level PWM creating a new amplifier scheme: A3, 1-bit feedback extension of the open loop A1. In our implementation we selected the value of 10 nanoseconds as resolution of correction for the PWM waveform.
C cross point estimation and 3-level PWM creating a new amplifier scheme: A3, 1-bit feedback extension of the open loop A1. In our implementation we selected the value of 10 nanoseconds as resolution of correction for the PWM waveform.
With reference to max 70 Wrms delivered to a 4  speaker, Figures 9 and 10 compare the amplifier schemes A1, A2 and A3 in terms of power efficiency and THD. The maximum power efficiency, up to roughly 95% in Figure 9, is achieved by the open loop scheme A1. With such high-efficiency each power MOS of the full bridge is dissipating less than 1 W avoiding extra cooling hardware. These results outperform classic DAC plus analog amplifier solutions: as example the hybrid analog scheme in [5] has a maximum power efficiency below 77%. The schemes with feedback topologies, A2 and A3, achieve similar efficiency, higher than 90%, only for power levels higher than 25–30 Wrms. Concerning THD, the lower distortion is achieved around 40–50 Wrms. The minimum THD is below the target of 0.2%; the use of feedback schemes allows reaching the target THD on a wider frequency range versus the open loop A1 scheme. Between A2 and A3 amplifiers the latter is preferred since it improves the THD and sensitivity performance of A1 but with minimal complexity overhead and minimal efficiency losses.
speaker, Figures 9 and 10 compare the amplifier schemes A1, A2 and A3 in terms of power efficiency and THD. The maximum power efficiency, up to roughly 95% in Figure 9, is achieved by the open loop scheme A1. With such high-efficiency each power MOS of the full bridge is dissipating less than 1 W avoiding extra cooling hardware. These results outperform classic DAC plus analog amplifier solutions: as example the hybrid analog scheme in [5] has a maximum power efficiency below 77%. The schemes with feedback topologies, A2 and A3, achieve similar efficiency, higher than 90%, only for power levels higher than 25–30 Wrms. Concerning THD, the lower distortion is achieved around 40–50 Wrms. The minimum THD is below the target of 0.2%; the use of feedback schemes allows reaching the target THD on a wider frequency range versus the open loop A1 scheme. Between A2 and A3 amplifiers the latter is preferred since it improves the THD and sensitivity performance of A1 but with minimal complexity overhead and minimal efficiency losses.
4. Prototyped Digital Audio Amplifier
From the design space exploration carried out in Section 3 the amplifier architecture, summarized hereafter, resulted as an optimal trade-off between circuit complexity, power efficiency, output distortion and low sensitivity to parameter changes. The digital part includes: an oversampler by a factor  using an Equiripple 4-stage polyphase FIR interpolating filter, a cross point estimator based on
using an Equiripple 4-stage polyphase FIR interpolating filter, a cross point estimator based on  C technique realizing a NPWM scheme, a noise shaper with
C technique realizing a NPWM scheme, a noise shaper with  output bits and a 5th-order noise shaping filter, 3-level PWM generation, correction of PWM words through the insertion of time guard intervals also as a function of a 1-bit signal feedback.
output bits and a 5th-order noise shaping filter, 3-level PWM generation, correction of PWM words through the insertion of time guard intervals also as a function of a 1-bit signal feedback.
The digital processing part, implemented in HDL, has been synthesized in different CMOS standard-cells technologies (90 nm 1 V supply voltage and 180 nm 1.8 V supply voltage) resulting in a digital complexity of 15.2 Kgates, mainly due to the noise shaping and interpolating filters. The low circuit complexity allows the fitting of the digital circuitry on several low-cost SRAM-based FPGA devices. As example the processing part of the amplifier occupies 90% of a Xilinx Virtex XCV100 or 58% of a Xilinx Spartan3 200. Such devices are available for large volume production at a cost of few dollars. Hence the low circuit complexity of the proposed architecture allows for a low-cost implementation. The power consumption for the above cited implementations is in the order of few hundreds of mW, as example 100 mW when integrating the amplifier in the XCV100 and playing 44.1 kS/s CD-quality audio signals.
The output stage is a full bridge made up of N-/P- MOS devices from [26] plus a differential 4th-order LC Butterworth filter. Table 5 summarizes the measured results on the amplifier prototype. The THD value at 1 kHz refers to a 16-bit 44.1 kS/s CD-quality input signal and is evaluated using an Audio Precision test setup. The high power efficiency achieved permits an output power up to 70 Wrms without using extra cooling hardware. The results in Table 5 (Pmax of 70 Wrms, THD of 0.13% and efficiency of 94% at 45 Wrms) confirm the performance estimation made by simulations during the design phase in Sections 2 and 3, particularly in Figures 9 and 10 (Pmax of 70 Wrms, THD below 2% and efficiency up to 95% in the range 40–50 Wrms).
The prototype allowed us also to assess the performance improvement of the 1-bit compensating loop scheme. The sensitivity of the amplifier to parameter changes is an important feature against temperature variations, devices tolerances, power supply ripple. As example, Figure 11 shows how the THD degrades when the system configuration is optimised for 4  speaker and then the load is changed with an 8
speaker and then the load is changed with an 8  speaker. Both the cases with 1-bit feedback scheme (1b feedback) and without (open loop) are considered. From Figure 11 it is worth noting how the THD performance degradation due to parameter change is lower in the amplifier with feedback.
speaker. Both the cases with 1-bit feedback scheme (1b feedback) and without (open loop) are considered. From Figure 11 it is worth noting how the THD performance degradation due to parameter change is lower in the amplifier with feedback.
5. Comparison to the State of the Art and Future Work
5.1. Comparison to the State of the Art
When compared to the state of the art of digital input power amplifiers our prototype stands for its low-complexity, while keeping high power efficiency and low THD levels. The distortion levels, THD below 0.2% at 1 kHz in the power range 35–60 Wrms with a minimum of 0.13% at 45 Wrms (see A3 in Figure 10), are suitable for audio Hi-Fi applications. Other works in literature achieve lower THD values, as example in [13] the THD is 0.02% for similar power levels of 50 W, but at the expense of a lower efficiency and an increased complexity. The power efficiency is 80% in [13] while in our work is higher than 90%. The digital processing tasks in [13] require the use of multiple boards (1 DSP board for the digital audio processing plus 1 FPGA board for PWM processing) while our architecture just requires 1 low-cost FPGA having a bounded circuit complexity of 15 Kgates. The multiple boards digital amplifier in [13] features also a configuration with 90% power efficiency but with a THD of 0.2%. In [16] with a 9 level PWM inverter the achieved performances of 0.25% THD and 80% efficiency are worse than our results. This confirms our analysis in Section 3.4 that 3-level PWM is the optimal choice for the output stage. Compact solutions using a single chip for the digital part, as in our work, and without heatsink have been proposed in [9, 19, 23, 31, 32]. However [19] is missing the feedback scheme needed, as proved in Section 4, against parameter changes; in [9] the efficiency levels are lower than those achieved by our scheme. The FPGA-based audio amplifier in [23] is missing feedback and NPWM techniques; it has a power efficiency of 80% and a THD of 1% both worse than our achieved results. In [31, 32] only the interpolation filter is implemented occupying a whole Spartan FPGA. With respect to our previous conference paper [20], where only UPWM is implemented and a lower oversampling factor and a less-performance FIR interpolating filter are used, the audio processing system in this work has been improved including the digital techniques for NPWM, more accurate models for all the analog components, a more performing interpolating filter. The prototyped architecture in this work versus [20] achieves a much better THD value, predicted by the simulations and confirmed by measures on the prototype. Finally in some works [10, 17, 24], the shown results refer to simulations or prototypes only of the low-power PWM generator without including a real prototyped power stage. As discussed in this work, and widely proved in literature, the nonideal behaviour of the power stage is a key issue in power audio amplifiers.
5.2. Future Work
The proposed platform-based approach has been used also to define the optimal architecture of digital power audio amplifiers using other complementary power MOS devices, such as the IR530 and IR9530. The achieved results with these MOS devices prove that, targeting a power level of 45 Wrms on an 8  load, optimal distortion performances below 0.2% can be reached in the range 17–35 Wrms with a power efficiency higher than 90%. The resulting architecture is similar to that discussed in Section 4 with the exception of the tuning of some parameters specifically optimized for the characteristics of the new power devices.
load, optimal distortion performances below 0.2% can be reached in the range 17–35 Wrms with a power efficiency higher than 90%. The resulting architecture is similar to that discussed in Section 4 with the exception of the tuning of some parameters specifically optimized for the characteristics of the new power devices.
As work extension we are applying the same methodology to the design of a fully integrated digital input audio amplifier targeting maximum power levels of 1-2 W. Such amplifiers of few Watts are needed for battery-power terminals with audio playing capability [33, 34]. The design of the amplifier is carried out using an architecture similar to that in Section 4 fitted on a BCD 0.35  m technology providing CMOS transistors for the digital part and DMOS transistors for the analog power part. The only off-chip circuit is the LC lowpass filter. Postlayout characterization proves that the digital amplifier can be integrated in less than 2 mm2. The integrated power stage is an inverter with NDMOS sized with
m technology providing CMOS transistors for the digital part and DMOS transistors for the analog power part. The only off-chip circuit is the LC lowpass filter. Postlayout characterization proves that the digital amplifier can be integrated in less than 2 mm2. The integrated power stage is an inverter with NDMOS sized with  mm and
mm and  m supporting, with low
m supporting, with low  on of few m
on of few m , output currents of 0.14 A on output load of 100
, output currents of 0.14 A on output load of 100  .
.
6. Conclusions
The design of digital audio power amplifiers is presented in the paper. A modelling platform has been built to allow a fast but still accurate exploration of the mixed-signal design space which involves the codesign of (i) audio processing algorithms with physical characteristics of hardware components and of (ii) low-power integrated digital circuits with analog power devices. Different amplifier architectures have been modelled, simulated and compared to find optimal trade-offs among different cost-functions: low-distortion, high power efficiency, low circuit complexity and low sensitivity to parameter changes. The selected amplifier architecture has been prototyped, for power levels of tens of Watts, implementing the digital processing part on a single low-complexity FPGA while off-chip components are used for the power output stage, no heatsink is required. The resulting digital amplifier, compared with the state of the art, features a low circuit complexity while keeping good power efficiency, higher than 90%, and low-distortion levels, down to 0.13%. As future extension the realization of a fully integrated digital amplifier in BCD technology is presented for power levels of few Watts.
References
Self D: Audio Power Amplifier Design Handbook. 4th edition. Newnes, Oxford, UK; 2006.
Saponara S: Current-feedback architecture for high-slew-rate and low-THD high-end audio amplifier. Electronics Letters 2008,44(25):1433-1434. 10.1049/el:20082660
Walker G: A class B switch-mode assisted linear amplifier. IEEE Transactions on Power Electronics 2003,18(6):1278-1285. 10.1109/TPEL.2003.818825
Ginart AE, Bass RM, Leach WM Jr., Habetler TG: Analysis of the class AD audio amplifier including hysteresis effects. IEEE Transactions on Power Electronics 2003,18(2):679-685. 10.1109/TPEL.2003.809330
Saponara S, Terreni P: Switching-based topologies for high-efficiency audio amplifiers. Proceedings of the International Symposium on Signals, Circuits and Systems (ISSCS '05), 2005 1: 283-286.
Poulsen S, Andersen M: Hysteresis controller with constant switching frequency. IEEE Transactions on Consumer Electronics 2005,51(2):688-693. 10.1109/TCE.2005.1468020
Hiorns RE, Sandler MB: Power digital to analogue conversion using pulse width modulation and digital signal processing. IEE Proceedings G 1993,140(5):329-338.
Botti E, Grosso A, Meroni C, Stefani F: Digital input audio power amplifiers in 0.6- μ m BCD technology: two examples. Proceedings of the IEEE International Symposium on Power Semiconductor Devices & ICs (ISPSD '04), 2004, Kitakyushu, Japan 16: 93-96.
Grosso A, Botti E, Stefani F, Ghioni M: A 250 W audio amplifier with straightforward digital input-PWM output. Proceedings of the European Solid-State Circuits Conference (ESSCIRC '05), 2002 225-228.
Midya P, Roeckner B, Bergstedt S: Digital correction of PWM switching amplifiers. IEEE Power Electronics Letters 2004,2(2):68-72. 10.1109/LPEL.2004.834795
Nielsen K: PEDEC—a novel pulse referenced control method for high quality digital PWM switching power amplification. Proceedings of IEEE Power Electronics Specialist Conference (PESC '95), 1998 200-208.
Saponara S, Fanucci L, Terreni P: Oversampled and noise-shaped pulse-width modulator for high-fidelity digital audio amplifier. Proceedings of the IEEE International Conference on Electronics, Circuits, and Systems (ICECS '06), 2006, Nice, France 830-833.
Pascual C, Song Z, Krein PT, Sarwate DV, Midya P, Roeckner WBJ: High-fidelity PWM inverter for digital audio amplification: spectral analysis, real-time DSP implementation, and results. IEEE Transactions on Power Electronics 2003,18(1):473-485. 10.1109/TPEL.2002.807102
Gwee B-H, Chang JS, Adrian V: A micropower low-distortion digital class-D amplifier based on an algorithmic pulse width modulator. IEEE Transactions on Circuits and Systems I 2005,52(9):934-949.
Gwee B: Micropower low-distortion digital pulse width modulator for a digital class D amplifier. IEEE Transactions on Circuits and Systems II 2002,49(5):1-13.
Antunes VME, Silva JF, Fernão-Pires V: Experimental evaluation of a digital multi-level audio power amplifier. Proceedings of the IEEE Annual Power Electronics Specialists Conference (PESC '04), 2004 2: 1175-1179.
Vlassopoulos N, Reisis D, Lentaris G, et al.: An approach for efficient design of digital amplifiers. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '06), 2006 5531-5534.
Spectrum Design Solutions Inc : Digital audio solutions application brief. 2006.
Apogee : Direct digital amplification (DDX) white paper. 2002.
Saponara S, Terreni P: Mixed-signal design of a digital input power amplifier for automotive audio applications. Proceedings of the Conference on Design, Automation and Test in Europe (DATE '06), 2006 2: 212-216.
Jeong S-G, Park M-H: The analysis and compensation of dead time effects in PWM inverters. IEEE Transactions on Industrial Electronics 1991,38(2):108-114. 10.1109/41.88903
Goldberg JM, Sandler MB: Pseudo-natural pulse width modulation for high accuracy digital-to-analogue conversion. Electronics Letters 1991,27(16):1491-1492. 10.1049/el:19910933
Liu Y-H, Teng J-H, Hsieh C-H: Design and implementation of a fully-digital, high-efficiency class-D amplifier system. Proceedings of the IEEE Region 10th Annual International Conference (TENCON '07), 2007, Taipei, Taiwan 1-4.
Yoneya A: Pulse width and position modulation for fully digital audio amplifier. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '08), 2008, Seattle, Wash, USA 1692-1695.
Saponara S, Nuzzo P, Nani C, van der Plas G, Fanucci L: Architectural exploration and design of time-interleaved SAR arrays for low-power and high speed A/D converters. IEICE Transactions on Electronics 2009, E-92C: 843-851.
Infineon Technologies : Data sheet BSO200N03S, Optimos 2 Power-Transistor. rev 1.6, 2008
Cerezo J: Class D audio amplifier performance relationship to MOSFET parameters. International Rectifier AN 1070, 2005
Philips : Data sheet UDA1320ATS. January 2000
Turek D: Design of efficient digital interpolation filters for integer upsampling, M.S. thesis. MIT, Boston, Mass, USA; 2004.
Benameur N, Loulou M: Design of efficient digital interpolation filters and sigma-delta modulator for audio DAC. Proceedings of the IEEE 4th International Conference on Design & Technology of Integrated Systems in Nanoscal Era, (DTIS '09), 2008 1-7.
Jacobsohn P, Palmer D: Audio sample rate conversion in FPGAs. Xcell Journal 2007, 50-54.
Huang X, Han Y, Chen L: The design and FPGA verification of a general structure, area-optimized interpolation filter used in sigma-delta DAC. Proceedings of the IEEE International Conference on Solid-State and Integrated-Circuit Technology (ICSICT '06), October 2006, Shanghai, China 2111-2113.
Becker R, Groeneweg WH: An audio amplifier providing up to 1 Watt in standard digital 90-nm CMOS. IEEE Journal of Solid-State Circuits 2006,41(7):1648-1653. 10.1109/JSSC.2006.873674
Ryoo J-Y, Cho G-H: A single chip l W CMOS audio power amplifier with pseudo buffer analog and class D switching mixed mode for mobile application. IEICE Transactions on Electronics 2005,E-88C(9):1886-1892.
Acknowledgment
The work has been partially supported by the SHAPES FP6 EU project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saponara, S., Terreni, P. Mixed-Signal Architectures for High-Efficiency and Low-Distortion Digital Audio Processing and Power Amplification. J Embedded Systems 2010, 394070 (2009). https://doi.org/10.1155/2010/394070
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/394070






 -1 samples out of M are zeros (due to zero padding) and hence a polyphase structure reduces the required MAC operations for the interpolating filter by a factor M.
-1 samples out of M are zeros (due to zero padding) and hence a polyphase structure reduces the required MAC operations for the interpolating filter by a factor M.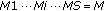 ) with a filter of reduced order
) with a filter of reduced order 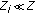 .
.


 C- and LI- NPWM.
C- and LI- NPWM.





