Abstract
This paper presents a novel ESPRIT algorithm-based joint angle and frequency estimation using multiple-delay output (MDJAFE). The algorithm can estimate the joint angles and frequencies, since the use of multiple output makes the estimation accuracy greatly improved when compared with a conventional algorithm. The useful behavior of the proposed algorithm is verified by simulations.
Similar content being viewed by others
1. Introduction
Antenna array has been used in many fields such as radar, sonar, electron reconnaissance and seismic data processing. The direction-of-arrival- (DOA-) estimation of signals impinging on an array of sensors is a fundamental problem in array processing [1–5]. Angle estimation and frequency estimation [6, 7] are two key problems in the signal processing field. The problem of joint DOA and frequency estimation arises in the applications of radar, wireless communications and electron reconnaissance. For example, these parameters can be applied to locate the radars and to locate pilot tones in electron reconnaissance systems [8]. Furthermore, a precise estimation of these parameters is helpful to attain a better pulse descriptor word (PDW) and thus enhances the system performance. Optimal techniques based on maximum likelihood [9] are often applicable but might be computationally prohibitive. Some ESPRIT-based joint angle and frequency estimation methods have been proposed in [10–14]. Zoltowski and Mathew [10] discuss this problem in the context of radar applications. Pro-ESPRIT is proposed to estimate angle and frequency. Haardt and Nossek [11] discuss the problem in the context of mobile communications for space division multiple access applications. Their method is based on Unitary-ESPRIT, which involves a certain transformation of the data to real valued matrices. Multi resolution ESPRIT is used for joint angle frequency estimation in [12]. ESPRIT method is used for frequency and angle estimation under uniform circular array in [13, 14]. References [15, 16] proposed the trilinear decomposition method for joint angle and frequency estimation method. The other joint angle and frequency estimation method is proposed in [17–24].
This paper uses multiple-delay output, so as to achieve the purpose of improving estimation accuracy. This algorithm has the improved performance compared with conventional method. The proposed algorithm is applicable to uniform linear array.
Note 1.
We denote by  the matrix transpose, and by
the matrix transpose, and by  the matrix conjugate transpose. The notation
the matrix conjugate transpose. The notation  refers to the Moore-Penrose inverse (pseudoinverse).
refers to the Moore-Penrose inverse (pseudoinverse).
2. The Data Model
There are  sources to reach uniform linear array with
sources to reach uniform linear array with  elements. Suppose that the i th source has a carrier frequency
elements. Suppose that the i th source has a carrier frequency  . The signal received at the
. The signal received at the  th antenna is
th antenna is

where  is direction of arrival (DOA) of the
is direction of arrival (DOA) of the  th signal, and
th signal, and  is array spacing.
is array spacing.  is the narrow-band signal of the
is the narrow-band signal of the  th source. In order to estimate frequency, we add
th source. In order to estimate frequency, we add  delayed outputs for the received signal of array antenna, as shown in Figure 1. We suppose that
delayed outputs for the received signal of array antenna, as shown in Figure 1. We suppose that  .
.
The delayed signal for (1) with delay  is
is

where  is velocity of light. We assume that channel state information is constant for
is velocity of light. We assume that channel state information is constant for  symbols.The received signal of array antennas without delay can be denoted as
symbols.The received signal of array antennas without delay can be denoted as

where the source matrix  and the direction matrix
and the direction matrix  are shown as follows
are shown as follows


where  ,
,  . According to (5), we define
. According to (5), we define

where  is the first
is the first  rows of
rows of  ,
,  is the last row of
is the last row of  .
.  is the second to the
is the second to the  th row of
th row of  ,
,  is the first row of
is the first row of  . The delayed signal for (2) with
. The delayed signal for (2) with  can be denoted as
can be denoted as

where

where  ,
,  .
.
The delayed signal for (2) with  can be denoted as
can be denoted as

According to (3), (7), and (9), we define

3. Joint Angle and Frequency Estimation
We can use received signal to attain the direction matrix  and the delay matrix
and the delay matrix  , and then estimate angle and frequency. The covariance matrix of the received signal can be reconstructed via
, and then estimate angle and frequency. The covariance matrix of the received signal can be reconstructed via  . Using eigenvalue decomposition of
. Using eigenvalue decomposition of  , we can get the signal subspace
, we can get the signal subspace  . In the free-noise case,
. In the free-noise case,  can be denoted as
can be denoted as

where  is a
is a  full-rank matrix.
full-rank matrix.
3.1. Frequency Estimation
According to (11),we define  and
and 

According to (12),

Let  , so
, so  . Because
. Because  has the same eigenvalues as
has the same eigenvalues as  , we use eigenvalue decomposition on
, we use eigenvalue decomposition on  to get
to get  ,
,  and then estimate frequency
and then estimate frequency  ,
,  . Using eigenvalue decomposition of
. Using eigenvalue decomposition of  , we can get the eigenvalues
, we can get the eigenvalues  ,
,  .
.

where angle  denotes taking the phase angles.
denotes taking the phase angles.
3.2. Angle Estimation
According to (11), take first to  th row of
th row of  to get
to get  , which is shown as follows
, which is shown as follows

Take second to  th row of
th row of  to get
to get  ,
,

We can get

where

where  ,
,  .
.
Let  , so
, so  . Because
. Because  has the same eigenvalues as
has the same eigenvalues as  , we use eigenvalue decomposition on
, we use eigenvalue decomposition on  to get
to get  ,
,  . And then estimate
. And then estimate  ,
,  . Using eigenvalue decomposition of
. Using eigenvalue decomposition of  , we can get the eigenvalues
, we can get the eigenvalues  ,
,  .
.

In contrast to ESPRIT algorithm [13], this algorithm has a high computational load, which is usually dominated by formation of the covariance matrix, matrix inversion and calculation of EVD. The major computational complexity of this algorithm is  , while ESPRIT requires
, while ESPRIT requires  , where
, where  ,
,  ,
,  , and
, and  are the number of antennas, delays, snapshots, and sources.
are the number of antennas, delays, snapshots, and sources.
4. Simulation Results
We present Monte Carlo simulations that are used to assess the angle and frequency estimation performance of MDJAFE algorithm. The number of Monte Carlo trials is 1000. Note that  is the number of antennas;
is the number of antennas;  is the number of the delays;
is the number of the delays;  is the number of snapshots;
is the number of snapshots;  is the number of the sources.
is the number of the sources.
Define  , where
, where  is the estimated angle/frequency, and
is the estimated angle/frequency, and  is the perfect angle/ frequency.
is the perfect angle/ frequency.
Simulation 1
The performance of this proposed algorithm is investigated.  ,
,  ,
,  , and
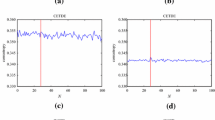
, and  in this simulation. Their DOAs are 10°, 20° and 30°), and their carrier frequencies are 500 kHZ, 700 kHZ and 900 kHZ. Figure 2 shows the performance of this proposed algorithm with
in this simulation. Their DOAs are 10°, 20° and 30°), and their carrier frequencies are 500 kHZ, 700 kHZ and 900 kHZ. Figure 2 shows the performance of this proposed algorithm with  dB, 30 dB. From Figures 2 and 3 we find that this proposed algorithm works well.
dB, 30 dB. From Figures 2 and 3 we find that this proposed algorithm works well.
Simulation 2
We compare this proposed algorithm with conventional method [13] which is without delay.  ,
,  ,
,  , and
, and  in this simulation. From Figure 4 we find that this proposed algorithm has better angle-frequency estimation performance than conventional method.
in this simulation. From Figure 4 we find that this proposed algorithm has better angle-frequency estimation performance than conventional method.
Simulation 3
MDJAFE algorithm performance under different snapshots  is investigated in this simulation.
is investigated in this simulation.  ,
,  , and
, and  in this simulation. Figure 5 shows the angle-frequency estimation performance under different
in this simulation. Figure 5 shows the angle-frequency estimation performance under different  . We find that the angle-frequency estimation performance of MDJAFE algorithm is improved with
. We find that the angle-frequency estimation performance of MDJAFE algorithm is improved with  increasing.
increasing.
Simulation 4
The performance of this algorithm under different source number  is investigated in the simulation.
is investigated in the simulation.  ,
,  , and
, and  in this simulation. The source number
in this simulation. The source number  is set to 2, 3, and 4. MDJAFE algorithm has different performance under different source numbers, as shown in Figure 6. From Figure 6, we find that angle and frequency estimation performance of MDJAFE algorithm degrades with the increase of the source number
is set to 2, 3, and 4. MDJAFE algorithm has different performance under different source numbers, as shown in Figure 6. From Figure 6, we find that angle and frequency estimation performance of MDJAFE algorithm degrades with the increase of the source number  .
.
Simulation 5
The performance of this algorithm under different antenna number  is investigated in the simulation.
is investigated in the simulation.  ,
,  , and
, and  in this simulation. The antenna number
in this simulation. The antenna number  is set to 8, 12, and 16. MDJAFE algorithm has different performance under different antenna number, as shown in Figure 7. From Figure 7, we find that angle and frequency estimation performance of MDJAFE algorithm is improved with
is set to 8, 12, and 16. MDJAFE algorithm has different performance under different antenna number, as shown in Figure 7. From Figure 7, we find that angle and frequency estimation performance of MDJAFE algorithm is improved with  increasing.
increasing.
Simulation 6
The performance of this algorithm under different delay number  is investigated in the simulation.
is investigated in the simulation.  ,
,  , and
, and  in this simulation. The delay number
in this simulation. The delay number  is set to 1, 2, 3, and 4. MDJAFE algorithm has different performance under different delay numbers, as shown in Figure 8. From Figure 8, we find that angle and frequency estimation performance of MDJAFE algorithm is improved with
is set to 1, 2, 3, and 4. MDJAFE algorithm has different performance under different delay numbers, as shown in Figure 8. From Figure 8, we find that angle and frequency estimation performance of MDJAFE algorithm is improved with  increasing.
increasing.
5. Conclusion
This work presents a new ESPRIT algorithm-based joint angle and frequency estimation using multiple-delay output. The advantage of this proposed algorithm using the multiple-delay output over the conventional algorithm is that the estimation accuracy has been greatly improved.
References
Widrow B, Stearns SD: Adaptive Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1985.
Zhang X, Xu D: Improved coherent DOA estimation algorithm for uniform linear arrays. International Journal of Electronics 2009, 96(2):213-222. 10.1080/00207210802526810
Zhang X, Gao X, Xu D: Multi-invariance ESPRIT-based blind DOA estimation for MC-CDMA with an antenna array. IEEE Transactions on Vehicular Technology 2009, 58(8):4686-4690.
Zhang X, Gao X, Chen W: Improved blind 2D-direction of arrival estimation with L-shaped array using shift invariance property. Journal of Electromagnetic Waves and Applications 2009, 23(5):593-606. 10.1163/156939309788019859
Zhang X, Yu J, Feng G, Xu D: Blind direction of arrival estimation of coherent sources using multi-invariance property. Progress In Electromagnetics Research 2008, 88: 181-195.
Rosnes E, Vahlin A: Frequency estimation of a single complex sinusoid using a generalized Kay estimator. IEEE Transactions on Communications 2006, 54(3):407-415.
Zhang XF, Xu DZ: Novel joint time delay and frequency estimation method. IET Radar, Sonar and Navigation 2009, 3(2):186-194. 10.1049/iet-rsn:20080032
Tsui J: Digital Techniques for Wideband Receivers. 2nd edition. Artech House, Norwood, Mass, USA; 2001.
Djeddou M, Belouchrani A, Aouada S: Maximum likelihood angle-frequency estimation in partially known correlated noise for low-elevation targets. IEEE Transactions on Signal Processing 2005, 53(8):3057-3064.
Zoltowski MD, Mathews CP: Real-time frequency and 2-D angle estimation with sub-Nyquistspatio-temporal sampling. IEEE Transactions on Signal Processing 1994, 42(10):2781-2794. 10.1109/78.324743
Haardt M, Nossek JA: 3-D unitary ESPRIT for joint 2-D angle and carrier estimation. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '97), April 1997, Munich, Germany 255-258.
Lemma AN, van der Veen AJ, Deprettere EF: Joint angle-frequency estimation using multi-resolution ESPRIT. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '98), May 1998, Seattle, Wash, USA 4: 1957-1960.
Lemma AN, van der Veen AJ, Deprettere EDF: Analysis of joint angle-frequency estimation using ESPRIT. IEEE Transactions on Signal Processing 2003, 51(5):1264-1283. 10.1109/TSP.2003.810306
Wang S, Zhou X: Direction-of-arrival and frequency estimation in array signal processing. Journal of Shanghai Jiaotong University 1999, 33(1):40-42.
Xiaofei Z, Gaopeng F, Jun Y, Dazhuan X: Angle-frequency estimation using trilinear decomposition of the oversampled output. Wireless Personal Communications 2009, 51(2):365-373. 10.1007/s11277-008-9652-5
Zhang X, Wang D, Xu D: Novel blind joint direction of arrival and frequency estimation for uniform linear array. Progress in Electromagnetics Research 2008, 86: 199-215.
Chen H, Wang Y, Wu Z: Frequency and 2-D angle estimation based on uniform circular array. Proceedings of IEEE International Symposium on Phased Array Systems and Technology, 2003 547-552.
Fu T, Jin S, Gao X: Joint 2-D angle and frequency estimation for uniform circular array. Proceedings of International Conference on Communications, Circuits and Systems (ICCCAS '06), June 2006 1: 230-233.
Jia W, Yao M, Song J: Joint frequency, two dimensional arrival angles estimations via marked signal subspace. Proceedings of the 8th International Conference on Signal Processing (ICSP '06), November 2006 1: 16-20.
Lin CH, Fang WH, Wu KH, Lin JD: Fast algorithm for joint azimuth and elevation angles, and frequency estimation via hierarchical space-time decomposition. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), April 2007 2: 1061-1064.
Hasan MA: DOA and frequency estimation using fast subspace algorithms. Signal Processing 1999, 77(1):49-62. 10.1016/S0165-1684(99)00022-5
Jiacai H, Yaowu S, Jianwu T: Joint estimation of DOA, frequency, and polarization based on cumulants and UCA. Journal of Systems Engineering and Electronics 2007, 18(4):704-709. 10.1016/S1004-4132(08)60007-9
Liang J, Zeng X, Ji B, Zhang J, Zhao F: A computationally efficient algorithm for joint range-DOA-frequency estimation of near-field sources. Digital Signal Processing 2009, 19(4):596-611. 10.1016/j.dsp.2008.06.006
Amin M, Zhang Y: Spatial time-frequency distributions and DOA estimation. Classical and Modern Direction-of-Arrival Estimation 2009, 185-217.
Acknowledgments
This paper is supported by China NSF Grant (60801052), Aeronautical Science Foundation of China (2009ZC52036), Ph.D. Programs Foundation of China's Ministry of Education (200802871056) and Nanjing University of Aeronautics and Astronautics Research Funding (NS2010109, NS2010114). The authors thank Professor Zhang Xiaofei for his help.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xudong, W. Joint Angle and Frequency Estimation Using Multiple-Delay Output Based on ESPRIT. EURASIP J. Adv. Signal Process. 2010, 358659 (2010). https://doi.org/10.1155/2010/358659
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/358659







 dB.
dB.



