Abstract
We introduce a new iterative scheme for finding a common element of the solutions sets of a finite family of equilibrium problems and fixed points sets of an infinite family of nonexpansive mappings in a Hilbert space. As an application, we solve a multiobjective optimization problem using the result of this paper.
Similar content being viewed by others

1. Introduction
Let  be a Hilbert space and
be a Hilbert space and  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a bifunction of
be a bifunction of  into
into  , where
, where  is the set of real numbers. The equilibrium problem for the bifunction
is the set of real numbers. The equilibrium problem for the bifunction  is to find
is to find  such that
such that

The set of solutions of the above inequality is denoted by  . Many problems arising from physics, optimization, and economics can reduce to finding a solution of an equilibrium problem.
. Many problems arising from physics, optimization, and economics can reduce to finding a solution of an equilibrium problem.
In 2007, S. Takahashi and W. Takahashi [1] first introduced an iterative scheme by the viscosity approximation method for finding a common element of the solutions set of equilibrium problem and the set of fixed points of a nonexpansive mapping in a Hilbert space  and proved a strong convergence theorem which is based on Combettes and Hirstoaga's result [2] and Wittmann's result [3]. More precisely, they obtained the following theorem.
and proved a strong convergence theorem which is based on Combettes and Hirstoaga's result [2] and Wittmann's result [3]. More precisely, they obtained the following theorem.
Theorem 1.1 (see [1]).
Let  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of  . Let
. Let  be a bifunction which satisfies the following conditions:
be a bifunction which satisfies the following conditions:
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(A3)For all  ,
,

(A4)For each  ,
,  is convex and lower semicontinuous.
is convex and lower semicontinuous.
Let  be a nonexpansive mapping with
be a nonexpansive mapping with  , where
, where  denotes the set of fixed points of the mapping
denotes the set of fixed points of the mapping  , and let
, and let  be a contraction, if there exists a constant
be a contraction, if there exists a constant  such that
such that  for all
for all  . Let
. Let  and
and  be the sequences generated by
be the sequences generated by  and
and

where  and
and  satisfy the following conditions:
satisfy the following conditions:

Then the sequences  and
and  converge strongly to a point
converge strongly to a point  , where
, where

 is the metric projection of
is the metric projection of  onto
onto  and
and  denotes nearest point in
denotes nearest point in  from
from  .
.
Recently, many results on equilibrium problems and fixed points problems in the context of the Hilbert space and Banach space are introduced (see, e.g., [4–8]).
Let  be a nonlinear mapping. The variational inequality problem corresponding to the mapping
be a nonlinear mapping. The variational inequality problem corresponding to the mapping  is to find a point
is to find a point  such that
such that

The variational inequality problem is denoted by  [9].
[9].
The mapping  is called
is called  -Lipschitzian and
-Lipschitzian and  -strongly monotone if there exist constants
-strongly monotone if there exist constants  such that
such that


respectively. It is well known that if  is strongly monotone and Lipschitzian on
is strongly monotone and Lipschitzian on  , then
, then  has a unique solution. An important problem is how to find a solution of
has a unique solution. An important problem is how to find a solution of  . Recently, there are many results to solve the
. Recently, there are many results to solve the  (see, e.g., [10–14]).
(see, e.g., [10–14]).
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  ,
,  be a countable family of nonexpansive mappings, and
be a countable family of nonexpansive mappings, and  be
be  bifunctions satisfying conditions (A1)–(A4) such that
bifunctions satisfying conditions (A1)–(A4) such that  . Let
. Let  . For each
. For each  , define the mapping
, define the mapping  by
by

Lemma 2.5 (see below) shows that, for each  ,
,  is firmly nonexpansive and hence nonexpansive and
is firmly nonexpansive and hence nonexpansive and  . Suppose that
. Suppose that  is a
is a  -Lipschitzian and
-Lipschitzian and  -strong monotone operator and let
-strong monotone operator and let  . Assume that
. Assume that  .
.
In this paper, motivated and inspired by the above research results, we introduce the following iterative process for finding an element in  : for an arbitrary initial point
: for an arbitrary initial point  ,
,

where  ,
,  ,
,  is a strictly decreasing sequence in
is a strictly decreasing sequence in  with
with  ,
,  ,
,  with
with  , and
, and  with
with  . Then we prove that the iterative process
. Then we prove that the iterative process  defined by (1.10) strongly converge to an element
defined by (1.10) strongly converge to an element  , which is the unique solution of the variational inequality
, which is the unique solution of the variational inequality

As an application of our main result, we solve a multiobjective optimization problem.
2. Preliminaries
Let  be a Hilbert space and
be a Hilbert space and  a nonexpansive mapping of
a nonexpansive mapping of  into itself such that
into itself such that  . For all
. For all  and
and  , we have
, we have

and hence

It is well known that, for all  and
and  ,
,

which implies that

for all  and
and  with
with  .
.
Let  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of  and, for any
and, for any  , there exists unique nearest point in
, there exists unique nearest point in  , denoted by
, denoted by  , such that
, such that

Moreover, we have the following:

Let  denote the identity operator of
denote the identity operator of  and let
and let  be a sequence in a Hilbert space
be a sequence in a Hilbert space  and
and  . Throughout this paper,
. Throughout this paper,  denotes that
denotes that  strongly converges to
strongly converges to  and
and  denotes that
denotes that  weakly converges to
weakly converges to  .
.
We need the following lemmas for our main results.
Lemma 2.1 (see [15]).
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  and
and  a nonexpansive mapping from
a nonexpansive mapping from  into itself. Then
into itself. Then  is demiclosed at zero, that is,
is demiclosed at zero, that is,

Lemma 2.2 (see [10, L mma 3.1(b)]).
mma 3.1(b)]).
Let  be a Hilbert space and
be a Hilbert space and  be a nonexpansive mapping. Let
be a nonexpansive mapping. Let  be a mapping which is
be a mapping which is  -Lipschitzian and
-Lipschitzian and  -strong monotone on
-strong monotone on  . Assume that
. Assume that  and
and  . Define a mapping
. Define a mapping  by
by

Then  for all
for all  , where
, where  .
.
If  , Lemma 2.2 still holds.
, Lemma 2.2 still holds.
Lemma 2.3 (see [16]).
Let  ,
,  be the sequences of nonnegative real numbers and
be the sequences of nonnegative real numbers and  . Suppose that
. Suppose that  is a real number sequence such that
is a real number sequence such that

Assume that  . Then the following results hold.
. Then the following results hold.
-
(1)
If
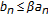 for all
for all  , where
, where 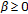 , then
, then 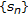 is a bounded sequence.
is a bounded sequence. -
(2)
If
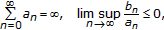 (2.10)
(2.10)
then  .
.
Lemma 2.4 (see [17]).
Let C be a nonempty closed and convex subset of a Hilbert space H and  be a bifunction which satisfies the conditions (A1)–(A4). Let
be a bifunction which satisfies the conditions (A1)–(A4). Let  and
and  . Then there exists
. Then there exists  such that
such that

Lemma 2.5 (see [2]).
Let  be a Hilbert space and
be a Hilbert space and  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of  . Assume that
. Assume that  satisfies the conditions (A1)–(A4). For all
satisfies the conditions (A1)–(A4). For all  and
and  , define a mapping
, define a mapping  as follows:
as follows:

Then the following holds:
(1) is single-valued;
is single-valued;
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,

(3) ;
;
(4) is closed and convex.
is closed and convex.
The following lemma is an immediate consequence of an inner product.
Lemma 2.6.
Let H be a real Hilbert space. Then the following identity holds:

3. Main Results
First, we prove some lemmas as follows.
Lemma 3.1.
The sequence  generated by (1.10) is bounded.
generated by (1.10) is bounded.
Proof.
Let  for each
for each  . Lemma 2.5 shows that each
. Lemma 2.5 shows that each  is firmly-nonexpansive and hence nonexpansive. Hence, for each
is firmly-nonexpansive and hence nonexpansive. Hence, for each  and
and  , we have
, we have


By Lemma 2.2, we have

where  . Therefore, by (3.2) and (3.3), we obtain (note that
. Therefore, by (3.2) and (3.3), we obtain (note that  is strictly decreasing and
is strictly decreasing and  )
)

By induction, we obtain  . Hence
. Hence  is bounded and so are
is bounded and so are  and
and  for each
for each  . Since
. Since  is
is  -Lipschitzian, we have
-Lipschitzian, we have

which shows that  is bounded. This completes the proof.
is bounded. This completes the proof.
Lemma 3.2.
If the following conditions hold:

then 
Proof.
For each  , since each
, since each  is nonexpansive, we have
is nonexpansive, we have

By (3.7), we have

By the definition of the iterative sequence (1.10), we have

and hence

It follows from (3.8) and (3.10) that

where  . Since
. Since  is strictly decreasing, we have
is strictly decreasing, we have  . Further, from the assumptions, it follows that
. Further, from the assumptions, it follows that

Therefore, by Lemma 2.3, we have  . This completes the proof.
. This completes the proof.
Lemma 3.3.
If the following conditions hold:

then  for each
for each  .
.
Proof.
For any  and
and  , it follows from Lemma 2.5(2) that
, it follows from Lemma 2.5(2) that

and hence  . Further, we have
. Further, we have

Therefore, from (2.4) and (3.3), we have

It follows that

for each  . Note that
. Note that  for
for  . From the assumptions, Lemma 3.2, and the previous inequality, we conclude that
. From the assumptions, Lemma 3.2, and the previous inequality, we conclude that  as
as  for each
for each  . Further, we have
. Further, we have

This completes the proof.
Lemma 3.4.
If the following conditions hold:

then  for all
for all 
Proof.
By the definition of the iterative sequence (1.10), we have

that is,

Hence, for any  , we get
, we get

Since each  is nonexpansive, by (2.2), we have
is nonexpansive, by (2.2), we have

Hence, combining this inequality with (3.22), we get

which implies that (note that  is a strictly decreasing sequence)
is a strictly decreasing sequence)

From Lemma 3.3,  , and the inequality
, and the inequality

we obtain

Therefore, from Lemma 3.2, (3.25), and (3.27), it follows that

This completes the proof.
Next we prove the main results of this paper.
Theorem 3.5.
Assume that the following conditions hold:

Then the sequence  generated by (1.10) converges strongly to an element in
generated by (1.10) converges strongly to an element in  , which is the unique solution of the variational inequality
, which is the unique solution of the variational inequality  .
.
Proof.
Since  , we can select an element
, we can select an element  , which implies that
, which implies that

First, we prove that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  such that
such that

Without loss of generality, we may further assume that  for some
for some  . From Lemmas 3.4 and 2.1, we get
. From Lemmas 3.4 and 2.1, we get  for all
for all  . Hence we have
. Hence we have  . It follows from Lemma 2.5 that each
. It follows from Lemma 2.5 that each  is firmly nonexpansive and hence nonexpansive. Lemma 3.3 shows that
is firmly nonexpansive and hence nonexpansive. Lemma 3.3 shows that  as
as  . Therefore, from Lemma 2.1, it follows that
. Therefore, from Lemma 2.1, it follows that  for each
for each  , which shows that
, which shows that  . Lemma 2.5 shows that
. Lemma 2.5 shows that  for each
for each  . Hence
. Hence  . By using the above argument, we conclude that
. By using the above argument, we conclude that

Noting that  is a solution of the
is a solution of the  , we obtain
, we obtain

It follows from Lemma 2.6 that

Let  and
and  for all
for all  . Then, from the assumptions and (3.31), we have
. Then, from the assumptions and (3.31), we have

Therefore, by applying Lemma 2.3 to (3.35), we conclude that the sequence  strongly converges to a point
strongly converges to a point  .
.
In order to prove the uniqueness of solution of the  , we assume that
, we assume that  is another solution of
is another solution of  . Similarly, we can conclude that
. Similarly, we can conclude that  converges strongly to a point
converges strongly to a point  . Hence
. Hence  , that is,
, that is,  is the unique solution of
is the unique solution of  . This completes the proof.
. This completes the proof.
As direct consequences of Theorem 3.5, we obtain the following corollaries.
Corollary 3.6.
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  . For each
. For each  let
let  be
be  bifunctions which satisfy conditions (A1)–(A4) such that
bifunctions which satisfy conditions (A1)–(A4) such that  . Let
. Let  , and let
, and let  be a strictly decreasing sequence with
be a strictly decreasing sequence with  ,
,  ,
,  with
with  ,
,  , and
, and  with
with  . For an arbitrary initial
. For an arbitrary initial  , define the iterative sequence
, define the iterative sequence  by
by

If the following conditions hold:

then the sequence  converges strongly to an element
converges strongly to an element  .
.
Proof.
Put  and
and  for each
for each  in Theorem 3.5. Then we know that
in Theorem 3.5. Then we know that  is
is  -Lipschitzian and
-Lipschitzian and  -strongly monotone,
-strongly monotone,  and
and  . Therefore, by Theorem 3.5, we conclude the desired result.
. Therefore, by Theorem 3.5, we conclude the desired result.
Corollary 3.7.
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  . Let
. Let  be a countable family of nonexpansive mappings of
be a countable family of nonexpansive mappings of  such that
such that  and
and  an operator which is
an operator which is  -Lipschitzian and
-Lipschitzian and  -strong monotone on
-strong monotone on  . Let
. Let  . Assume that
. Assume that  . Let
. Let  with
with  be a strictly decreasing sequence,
be a strictly decreasing sequence,  and
and  with
with  . For an arbitrary initial
. For an arbitrary initial  , define the iterative sequence
, define the iterative sequence  by
by

where  . If the following conditions hold:
. If the following conditions hold:

then the sequence  strongly converges to an element
strongly converges to an element  , which is the unique solution of the variational inequality
, which is the unique solution of the variational inequality

Proof.
Put  for each
for each  and
and  . Set
. Set  in Theorem 3.5. Then, by (2.6), we have
in Theorem 3.5. Then, by (2.6), we have  . Therefore, by Theorem 3.5, we conclude the desired result.
. Therefore, by Theorem 3.5, we conclude the desired result.
Remark 3.8.
-
(1)
Recently, many authors have studied the iteration sequences for infinite family of nonexpansive mappings. But our iterative sequence (1.10) is very different from others because we do not use
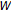 -mapping generated by the infinite family of nonexpansive mappings and we have no any restriction with the infinite family of nonlinear mappings.
-mapping generated by the infinite family of nonexpansive mappings and we have no any restriction with the infinite family of nonlinear mappings. -
(2)
We do not use Suzuki's lemma [18] for obtaining the result that
 . However, many authors have used Suzuki's lemma [18] for obtaining the result that
. However, many authors have used Suzuki's lemma [18] for obtaining the result that 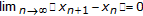 in the process of studying the similar algorithms. For example, see [5, 19, 20] and so on.
in the process of studying the similar algorithms. For example, see [5, 19, 20] and so on.
4. Application
In this section, we study a kind of multiobjective optimization problem based on the result of this paper. That is, we give an iterative sequence which solves the following multiobjective optimization problem with nonempty set of solutions:

where  and
and  are both convex and lower semicontinuous functions defined on a nonempty closed and convex subset of
are both convex and lower semicontinuous functions defined on a nonempty closed and convex subset of  of a Hilbert space
of a Hilbert space  . We denote by
. We denote by  the set of solutions of (4.1) and assume that
the set of solutions of (4.1) and assume that  .
.
We denote the sets of solutions of the following two optimization problems by  and
and  , respectively,
, respectively,

Obviously, if we find a solution  , then one must have
, then one must have  .
.
Now, let  and
and  be two bifunctions from
be two bifunctions from  to
to  defined by
defined by  and
and  , respectively. It is easy to see that
, respectively. It is easy to see that  and
and  , where
, where  denotes the set of solutions of the equilibrium problem:
denotes the set of solutions of the equilibrium problem:

respectively. In addition, it is easy to see that  and
and  satisfy the conditions (A1)–(A4). Therefore, by setting
satisfy the conditions (A1)–(A4). Therefore, by setting  in Corollary 3.6, we know that, for any initial guess
in Corollary 3.6, we know that, for any initial guess  ,
,

By Corollary 3.6, we know that the sequence  converges strongly to a solution
converges strongly to a solution  , which is a solution of the multiobjective optimization problem (4.1).
, which is a solution of the multiobjective optimization problem (4.1).
References
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Wittmann R: Approximation of fixed points of nonexpansive mappings. Archiv der Mathematik 1992,58(5):486–491. 10.1007/BF01190119
Ceng LC, Schaible S, Yao JC: Implicit iteration scheme with perturbed mapping for equilibrium problems and fixed point problems of finitely many nonexpansive mappings. Journal of Optimization Theory and Applications 2008,139(2):403–418. 10.1007/s10957-008-9361-y
Ceng LC, Petruşel A, Yao JC: Iterative approaches to solving equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Journal of Optimization Theory and Applications 2009,143(1):37–58. 10.1007/s10957-009-9549-9
Chang S-S, Cho YJ, Kim JK: Approximation methods of solutions for equilibrium problem in Hilbert spaces. Dynamic Systems and Applications 2008,17(3–4):503–513.
Cho YJ, Qin X, Kang JI: Convergence theorems based on hybrid methods for generalized equilibrium problems and fixed point problems. Nonlinear Analysis: Theory, Methods & Applications 2009,71(9):4203–4214. 10.1016/j.na.2009.02.106
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. Journal of Computational and Applied Mathematics 2009,225(1):20–30. 10.1016/j.cam.2008.06.011
Kinderlehrer D, Stampacchia G: An Introduction to Variational Inequalities and Their Applications, Pure and Applied Mathematics. Volume 88. Academic Press, New York, NY, USA; 1980:xiv+313.
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications (Haifa, 2000), Stud. Comput. Math.. Volume 8. Edited by: Butnariu D, Censor Y, Reich S. North-Holland, Amsterdam, The Netherlands; 2001:473–504.
Zeng LC, Ansari QH, Wu SY: Strong convergence theorems of relaxed hybrid steepest-descent methods for variational inequalities. Taiwanese Journal of Mathematics 2006,10(1):13–29.
Zeng LC, Wong NC, Yao JC: Convergence analysis of modified hybrid steepest-descent methods with variable parameters for variational inequalities. Journal of Optimization Theory and Applications 2007,132(1):51–69. 10.1007/s10957-006-9068-x
Ceng L-C, Xu H-K, Yao J-C: A hybrid steepest-descent method for variational inequalities in Hilbert spaces. Applicable Analysis 2008,87(5):575–589. 10.1080/00036810802140608
Xu HK, Kim TH: Convergence of hybrid steepest-descent methods for variational inequalities. Journal of Optimization Theory and Applications 2003,119(1):185–201.
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Maingé P-E: Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,325(1):469–479. 10.1016/j.jmaa.2005.12.066
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Colao V, Marino G, Xu H-K: An iterative method for finding common solutions of equilibrium and fixed point problems. Journal of Mathematical Analysis and Applications 2008,344(1):340–352. 10.1016/j.jmaa.2008.02.041
Chang S-S, Joseph Lee HW, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3307–3319. 10.1016/j.na.2008.04.035
Acknowledgment
This work was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, S., Cho, Y. & Qin, X. A New Iterative Method for Solving Equilibrium Problems and Fixed Point Problems for Infinite Family of Nonexpansive Mappings. Fixed Point Theory Appl 2010, 165098 (2010). https://doi.org/10.1155/2010/165098
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/165098



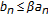 for all
for all  , where
, where 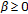 , then
, then 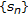 is a bounded sequence.
is a bounded sequence.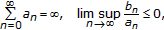
 -mapping generated by the infinite family of nonexpansive mappings and we have no any restriction with the infinite family of nonlinear mappings.
-mapping generated by the infinite family of nonexpansive mappings and we have no any restriction with the infinite family of nonlinear mappings. . However, many authors have used Suzuki's lemma [
. However, many authors have used Suzuki's lemma [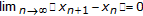 in the process of studying the similar algorithms. For example, see [
in the process of studying the similar algorithms. For example, see [