Abstract
The impulsive control method is developed to stabilize a class of neural networks with both time-varying and distributed delays. Some exponential stability criteria are obtained by using Lyapunov functionals, stability theory, and control by impulses. A numerical example is also provided to show the effectiveness and feasibility of the impulsive control method.
Similar content being viewed by others
1. Introduction
During the last decades, neural networks such as Hopfield neural networks, cellular neural networks, Cohen-Grossberg neural networks, and bidirectional associative memory neural networks have been extensively studied. There have appeared a number of important results; see [1–13] and references therein. It is well known that the properties of stability and convergence are important in design and application of neural networks, for example, when designing a neural network to solve linear programming problems and pattern recognition problems, we foremost guarantee that the models of neural network are stable. However, it may become unstable or even divergent because the model of a system is highly uncertain or the nature of the problem itself. So it is necessary to investigate stability and convergence of neural networks from the control point of view. It is known that impulses can make unstable systems stable or, otherwise, stable systems can become unstable after impulse effects; see [14–18]. The problem of stabilizing the solutions by imposing proper impulse controls has been used in many fields such as neural network, engineering, pharmacokinetics, biotechnology, and population dynamics [19–25]. Recently, several good impulsive control approaches for real world systems have been proposed; see [22–32]. In [26], Yang and Xu investigate the global exponential stability of Cohen-Grossberg neural networks with variable delays by establishing some impulsive differential inequalities. The criteria not only present an approach to stabilize the unstable neural networks by utilizing impulsive effects but also show that the stability still remains under certain impulsive perturbations for some continuous stable neural networks. In [27], Li et al. consider the impulsive control of Lotka-Volterra predator-prey system by employing the method of Lyapunov functions. In [28], Wang and Liu investigate the impulsive stabilization of delay differential systems via the Lyapunov-Razumikhin method. However, there are few results considering the impulsive stabilization of neural networks with both time-varying and distributed delays, which is very important in theories and applications and also is a very challenging problem.
Motivated by the above discussion, in this paper, we will investigate the impulsive stabilization for a class of neural networks with both time-varying and distributed delays. Some exponential stability criteria are obtained by using Lyapunov functionals, stability theory, and control by impulses. The organization of this paper is as follows. In the next section, the problems investigated in this paper are formulated, and some preliminaries are presented. We state and prove our main results in Section 3. Then, an illustrative example is given to show the effectiveness of the obtained impulsive control method in Section 4. Finally, concluding remarks are made in Section 5.
2. Model Description and Preliminaries
Let  denote the set of real numbers,
denote the set of real numbers,  the
the  -dimensional real space equipped with the Euclidean norm
-dimensional real space equipped with the Euclidean norm  and
and  the set of positive integral numbers.
the set of positive integral numbers.
Considering the following neural networks with both time-varying and distributed delays:

where  ,
,  corresponds to the number of units in a neural network,
corresponds to the number of units in a neural network,  is the state variable of the
is the state variable of the  th neuron,
th neuron,  denotes the passive delay rates,
denotes the passive delay rates,  ,
,  denote the connection weights of the unit
denote the connection weights of the unit  on the unit
on the unit  ,
,  ,
,  are the activation functions of the neurons,
are the activation functions of the neurons,  is the input of the unit
is the input of the unit  , and
, and  is the transmission delay of the
is the transmission delay of the  th neuron such that
th neuron such that  ,
,  ,
,  ,
,  , where
, where  ,
,  and
and  are some constants. And the system (2.1) is supplemented with initial values given by the form
are some constants. And the system (2.1) is supplemented with initial values given by the form

where  ,
,  denotes piecewise continuous functions defined on
denotes piecewise continuous functions defined on  . For
. For  ,
,  , let
, let  ,
, 
We also consider the impulses at times  ,
,  ,
,

where  are some undetermined constants.
are some undetermined constants.
Throughout this paper, we assume the following.
() are bounded and satisfy the following property:
are bounded and satisfy the following property:

where  ,
,  are constants for
are constants for 
() The delay kernels  ,
,  are piecewise continuous and satisfy
are piecewise continuous and satisfy  for all
for all  ,
,  , where
, where  is continuous and integrable.
is continuous and integrable.
()The impulse times  satisfy
satisfy  ,
,  .
.
Since  and
and  hold, by employing the well-known Brouwer's fixed point theorem, one can easily prove that there exists a unique equilibrium point for system (2.1).
hold, by employing the well-known Brouwer's fixed point theorem, one can easily prove that there exists a unique equilibrium point for system (2.1).
Assume that  is an equilibrium solution of system (2.1), then the transformation
is an equilibrium solution of system (2.1), then the transformation  ,
,  puts system (2.1) and (2.2) into the following form:
puts system (2.1) and (2.2) into the following form:

where  ,
,  ,
, 
3. Impulsive Stabilization of the Equilibrium Solution
Theorem 3.1.
Assume that ( )–(
)–( ) hold, then the equilibrium point of the system (2.1) can be exponentially stabilized by impulses if one of the following conditions hold.
) hold, then the equilibrium point of the system (2.1) can be exponentially stabilized by impulses if one of the following conditions hold.
()
() and
and  where
where

Proof.
First, we consider the following positive definite Lyapunov functional:

Then we can compute that

The time derivative of  along the trajectories of system (2.5) is obtained as
along the trajectories of system (2.5) is obtained as

Next we will consider conditions ( ) and (
) and ( ), respectively.
), respectively.
Case 1.
If  holds, that is,
holds, that is,  , then by (3.3) and (3.4), we get
, then by (3.3) and (3.4), we get

which implies that the equilibrium point of the system (2.1) is exponentially stable without impulses. So the conclusion of Theorem 3.1 holds obviously.
Case 2.
If  holds, then there exist
holds, then there exist  and
and  such that
such that

Then one may choose a sequence  such that
such that  and define
and define

It is obvious that  since (3.6) holds.
since (3.6) holds.
For any  , let
, let

For any  we can prove that for each solution
we can prove that for each solution  of system (2.5) through
of system (2.5) through  ,
,  implies that
implies that

First, for  , by (3.4), we have
, by (3.4), we have

Then considering (3.3) and the choice of  , we get
, we get

So we obtain

By the fact that  , we get
, we get

which, together with (3.6) and (3.7), yields

that is,

By following the similar inductive arguments as before, we derive that

This completes our proof of Case 2.
The proof of Theorem 3.1 is complete.
Corollary 3.2.
Assume that  ,
,  hold, then the equilibrium point of system (2.1) is exponentially stable if the following condition holds:
hold, then the equilibrium point of system (2.1) is exponentially stable if the following condition holds:

Corollary 3.3.
Assume that conditions in Theorem 3.1 hold, then the equilibrium point of the system (2.1) can be exponentially stabilized by periodic impulses.
Proof.
In fact, we need only to choose the sequence  such that
such that  and define
and define

As a special case of system (2.1), we consider the following neural network model:

we can obtain theorem as follows.
Theorem 3.4.
Assume that  hold, then the equilibrium point of the system (3.19) can be exponentially stabilized by impulses if one of the following conditions holds
hold, then the equilibrium point of the system (3.19) can be exponentially stabilized by impulses if one of the following conditions holds
 .
.
 and
and  where
where

Proof.
In fact, we need only to mention a few points since the rest is the same as in the proof of Theorem 3.1. First, instead of (3.4) we can get that

Second, instead of (3.6) and (3.7) we choose constants  and
and  such that
such that

Then one may choose a sequence  such that
such that  and define
and define

Corollary 3.5.
Assume that conditions in Theorem 3.4 hold, then the equilibrium point of the system (3.19) can be exponentially stabilized by periodic impulses.
Proof.
Here we need only to choose the sequence  such that
such that  . Let
. Let

4. A Numerical Example
In this section, we give an example to demonstrate the effectiveness of our method.
Example 4.1.
Consider the following neural network consisting two neurons:

Then  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  It is obvious that
It is obvious that  is an equilibrium point of system (4.1). By simple calculation, we get
is an equilibrium point of system (4.1). By simple calculation, we get

In this case, one may choose  ,
,  ,
,  such that (3.6) and (3.7) in Theorem 3.1 hold. According to Theorem 3.1, the equilibrium point
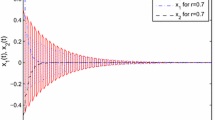
such that (3.6) and (3.7) in Theorem 3.1 hold. According to Theorem 3.1, the equilibrium point  of system (4.1) can be exponentially stabilized by impulses. The numerical simulation is shown in Figures 1(b) and 1(e).
of system (4.1) can be exponentially stabilized by impulses. The numerical simulation is shown in Figures 1(b) and 1(e).
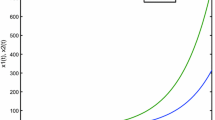
(a) Time-series of the  of system (4. 1) without impulsive control for
of system (4. 1) without impulsive control for  . (b) Time-series of the
. (b) Time-series of the  of system (4.1) by impulsive control with
of system (4.1) by impulsive control with  for
for  . (c) Time-series of the
. (c) Time-series of the  of system (4.1) by impulsive control with
of system (4.1) by impulsive control with  for
for  . (d) Phase portrait of system (4.1) without impulsive control for
. (d) Phase portrait of system (4.1) without impulsive control for  . (e) Phase portrait of system (4.1) by impulsive control with
. (e) Phase portrait of system (4.1) by impulsive control with  for
for  . (f) Phase portrait of system (4.1) by impulsive control with
. (f) Phase portrait of system (4.1) by impulsive control with  for
for  .
.
Remark 4.2.
Note that  , by Corollary 3.3, system (4.1) can be exponentially stabilized by periodic impulses.
, by Corollary 3.3, system (4.1) can be exponentially stabilized by periodic impulses.
Remark 4.3.
As we see from Figures 1(a) and 1(d), the equilibrium point  of system (4.1) without impulses is unstable. However, it becomes exponentially stable by explicit impulsive control (see Figures 1(b) and 1(e)). This implies that impulses may be used to exponentially stabilize some unable neural networks by our proposed control method. Furthermore, in the same impulse interval, if
of system (4.1) without impulses is unstable. However, it becomes exponentially stable by explicit impulsive control (see Figures 1(b) and 1(e)). This implies that impulses may be used to exponentially stabilize some unable neural networks by our proposed control method. Furthermore, in the same impulse interval, if  , then our control method in (3.6) and (3.7) is not satisfied. The equilibrium point
, then our control method in (3.6) and (3.7) is not satisfied. The equilibrium point  of system (4.1) cannot be exponentially stabilized by impulses, which is shown in Figures 1(c) and 1(f). However, one may observe that every solution of system (4.1) becomes a quasiperiodic solution because of the effects of impulses. Figures 1(a)–1(f) show the dynamic behavior of the system (4.1) with the initial condition
of system (4.1) cannot be exponentially stabilized by impulses, which is shown in Figures 1(c) and 1(f). However, one may observe that every solution of system (4.1) becomes a quasiperiodic solution because of the effects of impulses. Figures 1(a)–1(f) show the dynamic behavior of the system (4.1) with the initial condition  ,
,  ,
,  ,
, 
5. Conclusions
In this paper, we have investigated impulsive control for neural networks with both time-varying and distributed delays. By using Lyapunov functionals, stability theory, and control by impulses, some sufficient conditions are derived to exponentially stabilize neural networks with both time-varying and distributed delays. Simulation results of a neural network under impulsive control verify the effectiveness of the proposed control method.
References
Park JH, Park CH, Kwon OM, Lee SM: A new stability criterion for bidirectional associative memory neural networks of neutral-type. Applied Mathematics and Computation 2008,199(2):716-722. 10.1016/j.amc.2007.10.032
Cao J, Liang J, Lam J: Exponential stability of high-order bidirectional associative memory neural networks with time delays. Physica D 2004,199(3-4):425-436. 10.1016/j.physd.2004.09.012
Gopalsamy K: Stability of artificial neural networks with impulses. Applied Mathematics and Computation 2004,154(3):783-813. 10.1016/S0096-3003(03)00750-1
Hopfield J: Neurons with graded response have collective computational properties like those of two-state neurons. Proceedings of the National Academy of Sciences of the United States of America 1984,81(10):3088-3092. 10.1073/pnas.81.10.3088
Liu M: Global asymptotic stability analysis of discrete-time Cohen-Grossberg neural networks based on interval systems. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2403-2411. 10.1016/j.na.2007.08.019
Huang Z, Xia Y: Global exponential stability of BAM neural networks with transmission delays and nonlinear impulses. Chaos, Solitons & Fractals 2008,38(2):489-498. 10.1016/j.chaos.2006.11.032
Zhang J, Jin Z, Yan J, Sun G: Stability and Hopf bifurcation in a delayed competition system. Nonlinear Analysis: Theory, Methods & Applications 2009,70(2):658-670. 10.1016/j.na.2008.01.002
Lou X-Y, Cui B-T: Novel global stability criteria for high-order Hopfield-type neural networks with time-varying delays. Journal of Mathematical Analysis and Applications 2007,330(1):144-158. 10.1016/j.jmaa.2006.07.058
Yang Z, Xu D: Global exponential stability of Hopfield neural networks with variable delays and impulsive effects. Applied Mathematics and Mechanics 2006,27(11):1517-1522. 10.1007/s10483-006-1109-1
Zhang Y, Sun J: Stability of impulsive neural networks with time delays. Physics Letters A 2005,348(1-2):44-50. 10.1016/j.physleta.2005.08.030
Syed Ali M, Balasubramaniam P: Robust stability for uncertain stochastic fuzzy BAM neural networks with time-varying delays. Physics Letters A 2008,372(31):5159-5166. 10.1016/j.physleta.2008.05.067
Li X, Chen Z: Stability properties for Hopfield neural networks with delays and impulsive perturbations. Nonlinear Analysis: Theory, Methods & Applications 2009, 10: 3253-3265.
Xu D, Yang Z: Impulsive delay differential inequality and stability of neural networks. Journal of Mathematical Analysis and Applications 2005,305(1):107-120. 10.1016/j.jmaa.2004.10.040
Baĭnov DD, Simeonov PS: Systems with Impulse Effect: Stability, Theory and Applications, Ellis Horwood Series: Mathematics and Its Applications. Ellis Horwood, Chichester, UK; 1989:255.
Fu X, Yan B, Liu Y: Introduction of Impulsive Differential Systems. Science Press, Beijing, China; 2005.
Fu X, Li X:
 -stability theorems of nonlinear impulsive functional differential systems. Journal of Computational and Applied Mathematics 2008,221(1):33-46. 10.1016/j.cam.2007.10.020
-stability theorems of nonlinear impulsive functional differential systems. Journal of Computational and Applied Mathematics 2008,221(1):33-46. 10.1016/j.cam.2007.10.020Li X: Oscillation properties of higher order impulsive delay differential equations. International Journal of Difference Equations 2007,2(2):209-219.
Fu X, Li X: Oscillation of higher order impulsive differential equations of mixed type with constant argument at fixed time. Mathematical and Computer Modelling 2008,48(5-6):776-786. 10.1016/j.mcm.2007.11.006
Liu X: Stability results for impulsive differential systems with applications to population growth models. Dynamics and Stability of Systems 1994,9(2):163-174. 10.1080/02681119408806175
Ballinger G, Liu X: Practical stability of impulsive delay differential equations and applications to control problems. In Optimization Methods and Applications, Applied Optimization. Volume 52. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:3-21.
Stamova IM, Stamov GT: Lyapunov-Razumikhin method for impulsive functional differential equations and applications to the population dynamics. Journal of Computational and Applied Mathematics 2001,130(1-2):163-171. 10.1016/S0377-0427(99)00385-4
Sun J, Zhang Y: Impulsive control of Rössler systems. Physics Letters A 2003,306(5-6):306-312. 10.1016/S0375-9601(02)01499-8
Li Y, Liao X, Li C, Huang T, Yang D: Impulsive synchronization and parameter mismatch of the three-variable autocatalator model. Physics Letters A 2007,366(1-2):52-60. 10.1016/j.physleta.2006.12.073
Zhang Y, Sun J: Controlling chaotic Lu systems using impulsive control. Physics Letters A 2005,342(3):256-262. 10.1016/j.physleta.2005.05.059
Liu B, Teo KL, Liu X: Robust exponential stabilization for large-scale uncertain impulsive systems with coupling time-delays. Nonlinear Analysis: Theory, Methods & Applications 2008,68(5):1169-1183. 10.1016/j.na.2006.12.025
Yang Z, Xu D: Impulsive effects on stability of Cohen-Grossberg neural networks with variable delays. Applied Mathematics and Computation 2006,177(1):63-78. 10.1016/j.amc.2005.10.032
Li D, Wang S, Zhang X, Yang D: Impulsive control of uncertain Lotka-Volterra predator-prey system. Chaos, Solitons & Fractals. In press
Wang Q, Liu X: Impulsive stabilization of delay differential systems via the Lyapunov-Razumikhin method. Applied Mathematics Letters 2007,20(8):839-845. 10.1016/j.aml.2006.08.016
Weng A, Sun J: Impulsive stabilization of second-order delay differential equations. Nonlinear Analysis: Real World Applications 2007,8(5):1410-1420. 10.1016/j.nonrwa.2006.07.008
Luo Z, Shen J: Impulsive stabilization of functional differential equations with infinite delays. Applied Mathematics Letters 2003,16(5):695-701. 10.1016/S0893-9659(03)00069-7
Luo Z, Shen J: New Razumikhin type theorems for impulsive functional differential equations. Applied Mathematics and Computation 2002,125(2-3):375-386. 10.1016/S0096-3003(00)00139-9
Liu X: Impulsive stabilization of nonlinear systems. IMA Journal of Mathematical Control and Information 1993,10(1):11-19. 10.1093/imamci/10.1.11
Acknowledgment
The work is supported by the Science and Technology Programs of Shandong Province (2008GG30009008).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yin, L., Li, X. Impulsive Stabilization for a Class of Neural Networks with Both Time-Varying and Distributed Delays. Adv Differ Equ 2009, 859832 (2009). https://doi.org/10.1155/2009/859832
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/859832




 -stability theorems of nonlinear impulsive functional differential systems. Journal of Computational and Applied Mathematics 2008,221(1):33-46. 10.1016/j.cam.2007.10.020
-stability theorems of nonlinear impulsive functional differential systems. Journal of Computational and Applied Mathematics 2008,221(1):33-46. 10.1016/j.cam.2007.10.020