Abstract
We prove some results on the existence of fixed points for multivalued generalized  -contractive maps not involving the extended Hausdorff metric. Consequently, several known fixed point results are either generalized or improved.
-contractive maps not involving the extended Hausdorff metric. Consequently, several known fixed point results are either generalized or improved.
Similar content being viewed by others
1. Introduction
Throughout this paper, unless otherwise specified,  is a metric space with metric
is a metric space with metric  . Let
. Let 
 , and
, and  denote the collection of nonempty subsets of
denote the collection of nonempty subsets of  , nonempty closed subsets of
, nonempty closed subsets of  , and nonempty closed bounded subsets of
, and nonempty closed bounded subsets of  , respectively. Let
, respectively. Let  be the Hausdorff metric on
be the Hausdorff metric on  , that is,
, that is,

A multivalued map  is called
is called
(i)contraction [1] if for a fixed constant  and for each
and for each 

(ii)generalized contraction [2] if for any 

where  is a function from
is a function from  to
to  with
with  for every
for every  ;
;
(iii)contractive [3] if there exist constants  such that for any
such that for any  there is
there is  satisfying
satisfying

where  ;
;
(iv)generalized contractive [4] if there exist  such that for any
such that for any  there is
there is  satisfying
satisfying

where  is a function from
is a function from  to
to  with
with  for every
for every 
An element  is called a fixed point of a multivalued map
is called a fixed point of a multivalued map  if
if  . We denote
. We denote 
A sequence  in
in  is called an
is called an  of
of  at
at  if
if  for all
for all  . A map
. A map  is called lower semicontinuous if for any sequence
is called lower semicontinuous if for any sequence  with
with  imply that
imply that  .
.
Using the concept of Hausdorff metric, Nadler Jr. [1] established the following fixed point result for multivalued contraction maps which in turn is a generalization of the well-known Banach contraction principle.
Theorem 1.1 (see [1]).
Let  be a complete space and let
be a complete space and let  be a contraction map. Then
be a contraction map. Then 
This result has been generalized in many directions. For instance, Mizoguchi and Takahashi [2] have obtained the following general form of the Nadler's theorem.
Theorem 1.2 (see [2]).
Let  be a complete space and let
be a complete space and let  be a generalized contraction map. Then
be a generalized contraction map. Then 
Another extension of Nadler's result obtained recently by Feng and Liu [3]. Without using the concept of the Hausdorff metric, they proved the following result.
Theorem 1.3 (see [3]).
Let X be a complete space and let  be a multivalued contractive map. Suppose that a real-valued function
be a multivalued contractive map. Suppose that a real-valued function  on
on  ,
,  , is lower semicontinuous. Then
, is lower semicontinuous. Then 
Most recently, Klim and Wardowski [4] generalized Theorem 1.3 as follows:
Theorem 1.4 (see [4]).
Let X be a complete metric space and let  be a multivalued generalized contractive map such that a real-valued function
be a multivalued generalized contractive map such that a real-valued function  on
on  ,
,  is lower semicontinuous. Then
is lower semicontinuous. Then 
Recently, Kada et al. [5] introduced the concept of  -distance on a metric space as follows.
-distance on a metric space as follows.
A function  is called
is called  -
- on
on  if it satisfies the following for any
if it satisfies the following for any  :
:
()
() a map  is lower semicontinuous;
is lower semicontinuous;
() for any  there exists
there exists  such that
such that  and
and  imply
imply 
Using the concept of  -distance, they improved Caristi's fixed point theorem, Ekland's variational principle, and Takahashi's existence theorem. In [6], Susuki and Takahashi proved a fixed point theorem for contractive type multivalued maps with respect to
-distance, they improved Caristi's fixed point theorem, Ekland's variational principle, and Takahashi's existence theorem. In [6], Susuki and Takahashi proved a fixed point theorem for contractive type multivalued maps with respect to  -distance. See also [7–12].
-distance. See also [7–12].
Let us give some examples of  -distance [5].
-distance [5].
-
(a)
The metric
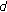 is a
is a  -distance on
-distance on 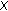 .
. -
(b)
Let
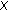 be normed space with norm
be normed space with norm 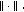 Then the functions
Then the functions 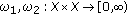 defined by
defined by 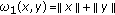 and
and 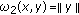 for every
for every  , are
, are  -distance.
-distance.
The following lemmas concerning  -distance are crucial for the proofs of our results.
-distance are crucial for the proofs of our results.
Lemma 1.5 (see [5]).
Let
 and
and
 be sequences in
be sequences in
 and let
and let
 and
and
 be sequences in
be sequences in
 converging to
converging to
 Then, for the w-distance
Then, for the w-distance
 on
on
 the following hold for every
the following hold for every
 :
:
(a)if  and
and  for any
for any  then
then  in particular, if
in particular, if  and
and  then
then  ;
;
-
(b)
if
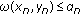 and
and 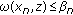 for any
for any 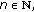 then
then  converges to
converges to  ;
; -
(c)
if
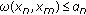 for any
for any  with
with 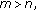 then
then 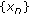 is a Cauchy sequence;
is a Cauchy sequence; -
(d)
if
 for any
for any 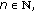 then
then  is a Cauchy sequence.
is a Cauchy sequence.
Lemma 1.6 (see [9]).
Let  be a closed subset of
be a closed subset of  and let
and let  be a w-distance on
be a w-distance on  Suppose that there exists
Suppose that there exists  such that
such that  . Then
. Then  (where
(where  )
)
We say a multivalued map  is generalized
is generalized  -contractive if there exist a
-contractive if there exist a  -distance
-distance  on
on  and a constant
and a constant  such that for any
such that for any  there is
there is  satisfying
satisfying

where  and
and  is a function from
is a function from  to
to  with
with  for every
for every 
Note that if we take  then the definition of generalized
then the definition of generalized  -contractive map reduces to the definition of generalized contractive map due to Klim and Wardowski [4]. In particular, if we take a constant map
-contractive map reduces to the definition of generalized contractive map due to Klim and Wardowski [4]. In particular, if we take a constant map  then the map
then the map  is weakly contractive (in short,
is weakly contractive (in short,  -contractive) [8], and further if we take
-contractive) [8], and further if we take  then we obtain
then we obtain  and
and  is contractive [3].
is contractive [3].
In this paper, using the concept of  -distance, we first establish key lemma and then obtain fixed point results for multivalued generalized
-distance, we first establish key lemma and then obtain fixed point results for multivalued generalized  -contractive maps not involving the extended Hausdorff metric. Our results either generalize or improve a number of fixed point results including the corresponding results of Feng and Liu [3], Latif and Albar [8], and Klim and Wardowski [4].
-contractive maps not involving the extended Hausdorff metric. Our results either generalize or improve a number of fixed point results including the corresponding results of Feng and Liu [3], Latif and Albar [8], and Klim and Wardowski [4].
2. Results
First, we prove key lemma in the setting of metric spaces.
Lemma 2.1.
Let
 be a generalized
be a generalized
 -contractive map. Then, there exists an orbit
-contractive map. Then, there exists an orbit
 of
of
 in
in
 such that the sequence of nonnegative real numbers
such that the sequence of nonnegative real numbers
 is decreasing to zero and the sequence
is decreasing to zero and the sequence
 is Cauchy.
is Cauchy.
Proof.
Since for each  ,
,  is closed, the set
is closed, the set  is nonempty for any
is nonempty for any  Let
Let  be an arbitrary but fixed element of
be an arbitrary but fixed element of  . Since
. Since  is generalized
is generalized  -contractive, there is
-contractive, there is  such that
such that


Using (2.1) and (2.2), we have

Similarly, there is  such that
such that


Using (2.4) and (2.5), we have

From (2.5) and (2.1), it follows that

Continuing this process, we get an orbit  of
of  in
in  such that
such that 

Using (2.8), we get

and thus for all 


Note that the sequences  and
and  are decreasing, and thus convergent. Now, by the definition of the function
are decreasing, and thus convergent. Now, by the definition of the function  there exists
there exists  such that
such that

Thus, for any  there exists
there exists  such that
such that

and thus for all  we have
we have

Also, it follows from (2.9) that for all  ,
,

where  Note that for all
Note that for all  we have
we have

and thus

Now, since  we have
we have  and hence the decreasing sequence
and hence the decreasing sequence  converges to
converges to  . Now, we show that
. Now, we show that  is a Cauchy sequence. Note that for all
is a Cauchy sequence. Note that for all  ,
,

where  Now, for any
Now, for any 

and thus by Lemma 1.5,  is a Cauchy sequence.
is a Cauchy sequence.
Using Lemma 2.1, we obtain the following fixed point result which is an improved version of Theorem 1.4 and contains Theorem 1.3 as a special case.
Theorem 2.2.
Let  be a complete space and let
be a complete space and let  be a generalized
be a generalized  -contractive map. Suppose that a real-valued function
-contractive map. Suppose that a real-valued function  on
on  defined by
defined by  is lower semicontinous. Then there exists
is lower semicontinous. Then there exists  such that
such that  Further, if
Further, if  then
then  .
.
Proof.
Since  is a generalized
is a generalized  -contractive map, it follows from Lemma 2.1 that there exists a Cauchy sequence
-contractive map, it follows from Lemma 2.1 that there exists a Cauchy sequence  in
in  such that the decreasing sequence
such that the decreasing sequence  converges to 0. Due to the completeness of
converges to 0. Due to the completeness of  , there exists some
, there exists some  such that
such that  Since
Since  is lower semicontinuous, we have
is lower semicontinuous, we have

and thus,  Since
Since  and
and  is closed, it follows from Lemma 1.6 that
is closed, it follows from Lemma 1.6 that 
As a consequence, we also obtain the following fixed point result.
Corollary 2.3 (see [8]).
Let  be a complete space and let
be a complete space and let  be a
be a  -contractive map. If the real-valued function
-contractive map. If the real-valued function  on
on  defined by
defined by  is lower semicontinous, then there exists
is lower semicontinous, then there exists  such that
such that  Further, if
Further, if  then
then 
Applying Lemma 2.1, we also obtain a fixed point result for multivalued generalized  -contractive map satisfying another suitable condition.
-contractive map satisfying another suitable condition.
Theorem 2.4.
Let
 be a complete space and let
be a complete space and let
 be a generalized
be a generalized
 -contractive map. Assume that
-contractive map. Assume that

for every  with
with  Then
Then 
Proof.
By Lemma 2.1, there exists an orbit  of
of  , which is a Cauchy sequence in
, which is a Cauchy sequence in  . Due to the completeness of
. Due to the completeness of  , there exists
, there exists  such that
such that  Since
Since  is lower semicontinuous and
is lower semicontinuous and  it follows from the proof of Lemma 2.1 that for all
it follows from the proof of Lemma 2.1 that for all 

where  Also, we get
Also, we get

Assume that  Then, we have
Then, we have

which is impossible and hence  .
.
Corollary 2.5 (see [8]).
Let
 be a complete space and let
be a complete space and let
 be
be
 -contractive map. Assume that
-contractive map. Assume that

for every  with
with  Then
Then 
References
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969,30(2):475–488.
Mizoguchi N, Takahashi W: Fixed point theorems for multivalued mappings on complete metric spaces. Journal of Mathematical Analysis and Applications 1989,141(1):177–188. 10.1016/0022-247X(89)90214-X
Feng Y, Liu S: Fixed point theorems for multi-valued contractive mappings and multi-valued Caristi type mappings. Journal of Mathematical Analysis and Applications 2006,317(1):103–112. 10.1016/j.jmaa.2005.12.004
Klim D, Wardowski D: Fixed point theorems for set-valued contractions in complete metric spaces. Journal of Mathematical Analysis and Applications 2007,334(1):132–139. 10.1016/j.jmaa.2006.12.012
Kada O, Suzuki T, Takahashi W: Nonconvex minimization theorems and fixed point theorems in complete metric spaces. Mathematica Japonica 1996,44(2):381–391.
Suzuki T, Takahashi W: Fixed point theorems and characterizations of metric completeness. Topological Methods in Nonlinear Analysis 1996,8(2):371–382.
Ansari QH: Vectorial form of Ekeland-type variational principle with applications to vector equilibrium problems and fixed point theory. Journal of Mathematical Analysis and Applications 2007,334(1):561–575. 10.1016/j.jmaa.2006.12.076
Latif A, Albar WA: Fixed point results in complete metric spaces. Demonstratio Mathematica 2008,41(1):145–150.
Lin L-J, Du W-S: Some equivalent formulations of the generalized Ekeland's variational principle and their applications. Nonlinear Analysis: Theory, Methods & Applications 2007,67(1):187–199. 10.1016/j.na.2006.05.006
Suzuki T: Several fixed point theorems in complete metric spaces. Yokohama Mathematical Journal 1997,44(1):61–72.
Takahashi W: Nonlinear Functional Analysis: Fixed Point Theory and Its Application. Yokohama, Yokohama, Japan; 2000:iv+276.
Ume JS, Lee BS, Cho SJ: Some results on fixed point theorems for multivalued mappings in complete metric spaces. International Journal of Mathematics and Mathematical Sciences 2002,30(6):319–325. 10.1155/S0161171202110350
Acknowledgment
The authors thank the referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Latif, A., Abdou, A.A.N. Fixed Points of Generalized Contractive Maps. Fixed Point Theory Appl 2009, 487161 (2009). https://doi.org/10.1155/2009/487161
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/487161



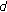 is a
is a  -distance on
-distance on 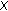 .
.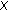 be normed space with norm
be normed space with norm 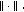 Then the functions
Then the functions 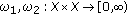 defined by
defined by 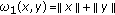 and
and 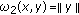 for every
for every  , are
, are  -distance.
-distance.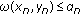 and
and 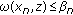 for any
for any 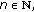 then
then  converges to
converges to  ;
;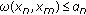 for any
for any  with
with 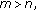 then
then 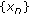 is a Cauchy sequence;
is a Cauchy sequence; for any
for any 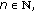 then
then  is a Cauchy sequence.
is a Cauchy sequence.