Abstract
The shadowing property is to find an exact solution to an iterated map that remains close to an approximate solution. In this article, using shadowing property, we show the stability of the following equation in normed group:  , where
, where  ,
,  and
and  is a mapping. And we prove that the even mapping which satisfies the above equation is quadratic and also the Hyers-Ulam stability of the functional equation in Banach spaces.
is a mapping. And we prove that the even mapping which satisfies the above equation is quadratic and also the Hyers-Ulam stability of the functional equation in Banach spaces.
Similar content being viewed by others
1. Introduction
The notion of pseudo-orbits very often appears in several areas of the dynamical systems. A pseudo-orbit is generally produced by numerical simulations of dynamical systems. One may consider a natural question which asks whether or not this predicted behavior is close to the real behavior of system. The above property is called the shadowing property (or pseudo-orbit tracing property). The shadowing property is an important feature of stable dynamical systems. Moreover, a dynamical system satisfying the shadowing property is in many respects close to a (topologically, structurally) stable system. It is well known that the shadowing property is a useful notion for the study about the stability theory, and the concept of the shadowing is close to this of the stability in dynamical systems.
In this paper, we are going to investigate the stability of functional equations using the shadowing property derived from dynamical systems.
The study of stability problems for functional equations is related to the following question raised by Ulam [1] concerning the stability of group homomorphisms. Let  be a group, and let
be a group, and let  be a metric group with the metric
be a metric group with the metric  Given
Given  does there exist a
does there exist a  such that if a mapping
such that if a mapping  satisfies the inequality
satisfies the inequality

for all  then a homomorphism
then a homomorphism  exists with
exists with  for all
for all 
-
D.
H. Hyers [2] provided the first partial solution of Ulam's question as follows. Let
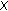 and
and 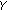 be Banach spaces with norms
be Banach spaces with norms 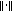 and
and  respectively. Hyers showed that if a function
respectively. Hyers showed that if a function  satisfies the following inequality:
satisfies the following inequality:

for some  and for all
and for all  then the limit
then the limit

exists for each  and
and  is the unique additive function such that
is the unique additive function such that

for any  Moreover, if
Moreover, if  is continuous in
is continuous in  for each fixed
for each fixed  then
then  is linear.
is linear.
Hyers' theorem was generalized in various directions. The very first author who generalized Hyers' theorem to the case of unbounded control functions was T. Aoki [3]. In 1978 Th. M. Rassias [4] by introducing the concept of the unbounded Cauchy difference generalized Hyers's Theorem for the stability of the linear mapping between Banach spaces. Afterward Th. M. Rassias's Theorem was generalized by many authors; see [5–7].
The quadratic function  satisfies the functional equation
satisfies the functional equation

Hence this equation is called the quadratic functional equation, and every solution of the quadratic equation (1.5) is called a quadratic function.
A Hyers-Ulam stability theorem for the quadratic functional equation (1.5) was first proved by Skof [8] for functions  where
where  is a normed space, and
is a normed space, and  is a Banach space. Cholewa [9] noticed that the theorem of Skof is still true if the relevant domain
is a Banach space. Cholewa [9] noticed that the theorem of Skof is still true if the relevant domain  is replaced by an abelian group. Several functional equations have been investigated in [10–12].
is replaced by an abelian group. Several functional equations have been investigated in [10–12].
From now on, we let  be an even integer, and
be an even integer, and  such that
such that  We denote
We denote  In this paper, we investigate that a mapping
In this paper, we investigate that a mapping  satisfies the following equation:
satisfies the following equation:

for a mapping  We will prove the stability in normed group by using shadowing property and also the Hyers-Ulam stability of each functional equation in Banach spaces.
We will prove the stability in normed group by using shadowing property and also the Hyers-Ulam stability of each functional equation in Banach spaces.
2. A Generalized Quadratic Functional Equation in Several Variables
Lemma 2.1.
Let  be an even integer number,
be an even integer number,  with
with  and
and  vector spaces. If an even mapping
vector spaces. If an even mapping  which satisfies
which satisfies

then  is quadratic, for all
is quadratic, for all 
Proof.
By letting  in the equation (2.1), we have
in the equation (2.1), we have

Since  we have
we have

that is,  By the assumption
By the assumption  we have
we have  Now, by letting
Now, by letting  and
and  we get
we get

for all  Since
Since  is even, we have
is even, we have

for all  From the following equation:
From the following equation:

we have

Now letting  and
and  we have
we have

Hence

for all  Then it is easily obtained that
Then it is easily obtained that  is quadratic. This completes the proof.
is quadratic. This completes the proof.
We call this quadratic mapping a generalized quadratic mapping of r-type.
3. Stability Using Shadowing Property
In this section, we will take  that is, we will investigate the generalized mappings of 1-type, and hence we will study the stability of the following functional equation by using shadowing property:
that is, we will investigate the generalized mappings of 1-type, and hence we will study the stability of the following functional equation by using shadowing property:

for all  where
where  is a commutative semigroup.
is a commutative semigroup.
Before we proceed, we would like to introduce some basic definitions concerning shadowing and concepts to establish the stability; see [13]. After then we will investigate the stability of the given functional equation based on ideas from dynamical systems.
Let us introduce some notations which will be used throughout this section. We denote  the set of all nonnegative integers,
the set of all nonnegative integers,  a complete normed space,
a complete normed space,  the closed ball centered at
the closed ball centered at  with radius
with radius  and let
and let  be given.
be given.
Definition 3.1.
Let  A sequence
A sequence  in
in  is a
is a  - pseudo-orbit for
- pseudo-orbit for  if
if

A 0-pseudo-orbit is called an orbit.
Definition 3.2.
Let  be given. A function
be given. A function  is locally
is locally  -invertible at
-invertible at  if for any point
if for any point  in
in  there exists a unique element
there exists a unique element  in
in  such that
such that  If
If  is locally
is locally  -invertible at each
-invertible at each  then we say that
then we say that  is locally
is locally -invertible.
-invertible.
For a locally  -invertible function
-invertible function  we define a function
we define a function  in such a way that
in such a way that  denote the unique
denote the unique  from the above definition which satisfies
from the above definition which satisfies  Moreover, we put
Moreover, we put

Theorem 3.3 (see [14]).
Let  be fixed, and let
be fixed, and let  be locally
be locally  -invertible. We assume additionally that
-invertible. We assume additionally that  Let
Let  and let
and let  be an arbitrary
be an arbitrary  -pseudo-orbit. Then there exists a unique
-pseudo-orbit. Then there exists a unique  such that
such that

Moreover,

Let  be a semigroup. Then the mapping
be a semigroup. Then the mapping  is called a (semigroup) norm if it satisfies the following properties:
is called a (semigroup) norm if it satisfies the following properties:
(1)for all 
(2)for all 
(3)for all  and also the equality holds when
and also the equality holds when  where
where  is the binary operation on
is the binary operation on 
Note that  is called a group norm if
is called a group norm if  is a group with an identity
is a group with an identity  , and it additionally satisfies that
, and it additionally satisfies that  if and only if
if and only if 
From now on, we will simply denote the identity  of
of  and the identity
and the identity  of
of  by 0. We say that
by 0. We say that  is a normed (semi)group if
is a normed (semi)group if  is a (semi)group with the (semi)group norm
is a (semi)group with the (semi)group norm  Now, given an Abelian group
Now, given an Abelian group  and
and  we define the mapping
we define the mapping  by the formula
by the formula

Since  is a normed group, it is clear that
is a normed group, it is clear that  is locally
is locally  -invertible at 0, and
-invertible at 0, and 
Also, we are going to need the following result. Tabor et al. proved the next lemma by using Theorem 3.3.
Lemma 3.4.
Let  Let
Let  be a commutative semigroup, and
be a commutative semigroup, and  a complete Abelian metric group. We assume that the mapping
a complete Abelian metric group. We assume that the mapping  is locally
is locally  -invertible and that
-invertible and that  Let
Let  satisfy the following two inequalities:
satisfy the following two inequalities:

where  are endomorphisms in
are endomorphisms in  , are endomorphisms in
, are endomorphisms in  We assume additionally that there exists
We assume additionally that there exists  such that
such that

Then there exists a unique function  such that
such that

Moreover, then  satisfies
satisfies

Proof.
Using the proof of [13, Theorem 2], one can easily show this lemma.
Let  ,
,  an even integer,
an even integer,  an Abelian group, and
an Abelian group, and  a complete normed Abelian group.
a complete normed Abelian group.
Theorem 3.5.
Let  be arbitrary, and let
be arbitrary, and let  be a function such that
be a function such that

for all  Then there exists a unique function
Then there exists a unique function  such that
such that

for all 
Proof.
By letting  in (3.11), we have
in (3.11), we have

Thus  Now, let
Now, let  in (3.11). From the inequality
in (3.11). From the inequality  , we have
, we have

Thus we obtain

for all  To apply Lemma 3.4 for the function
To apply Lemma 3.4 for the function  we may let
we may let

Then we have

Thus we also obtain  and so all conditions of Lemma 3.4 are satisfied. Hence we conclude that there exists a unique function
and so all conditions of Lemma 3.4 are satisfied. Hence we conclude that there exists a unique function  such that
such that

and also we have

Theorem 3.6.
Suppose that  is locally
is locally  -invertible,
-invertible,  is locally
is locally  -invertible, and
-invertible, and  is locally
is locally  -invertible. If a function
-invertible. If a function  satisfies the following equation:
satisfies the following equation:

for all  then
then  is a quadratic function.
is a quadratic function.
Proof.
By letting  in (3.20), we have
in (3.20), we have

By the uniqueness of the local division by  we get
we get  Also, setting
Also, setting  in (3.20),
in (3.20),  implies that
implies that

that is, we have

for all  By the uniqueness of the local division by
By the uniqueness of the local division by  we get
we get  for all
for all  Now, by letting
Now, by letting  and
and  in (3.20), we get
in (3.20), we get

for all  By the uniqueness of the local division by
By the uniqueness of the local division by  we have
we have

for all  Hence
Hence  is a quadratic mapping which completes the proof.
is a quadratic mapping which completes the proof.
Theorems 3.5 and 3.6 yield the following corollary.
Corollary 3.7.
Let  be a function satisfying (3.11), and let
be a function satisfying (3.11), and let  be arbitrary. Suppose that
be arbitrary. Suppose that  is locally
is locally  -invertible,
-invertible,  is locally
is locally  -invertible, and
-invertible, and  is locally
is locally  -invertible. Then there exists a quadratic function
-invertible. Then there exists a quadratic function  such that
such that

for all 
4. On Hyers-Ulam-Rassias Stabilities
In this section, let  be a normed vector space with norm
be a normed vector space with norm  a Banach space with norm
a Banach space with norm  and
and  an even integer. For the given mapping
an even integer. For the given mapping  we define
we define

for all 
Theorem 4.1.
Let  be an even mapping satisfying
be an even mapping satisfying  Assume that there exists a function
Assume that there exists a function  such that
such that


for all  Then there exists a unique generalized quadratic mapping of
Then there exists a unique generalized quadratic mapping of  -type
-type  such that
such that

for all 
Proof.
By letting  and
and  in (4.3), since
in (4.3), since  is an even mapping and
is an even mapping and  we have
we have

for all  Then we obtain that
Then we obtain that

for all 
Using (4.6), we have

for all  and all positive integer
and all positive integer  Hence we get
Hence we get

for all  and all positive integers
and all positive integers  and
and  with
with  Hence the sequence
Hence the sequence  is a Cauchy sequence. From the completeness of
is a Cauchy sequence. From the completeness of  we may define a mapping
we may define a mapping  by
by

for all  Since
Since  is even, so is
is even, so is  By the definition of
By the definition of  and (4.3), we have that
and (4.3), we have that

for all  Since
Since  the mapping
the mapping  is a generalized quadratic mapping of
is a generalized quadratic mapping of  -type by Lemma 2.1. Also, letting
-type by Lemma 2.1. Also, letting  and passing the limit
and passing the limit  in (4.8), we get (4.4).
in (4.8), we get (4.4).
To prove the uniqueness, suppose that  is another generalized quadratic mapping of
is another generalized quadratic mapping of  -type satisfying (4.4). Then we have
-type satisfying (4.4). Then we have

for all  as
as  Thus the generalized quadratic mapping
Thus the generalized quadratic mapping  is unique.
is unique.
Theorem 4.2.
Let  be an even mapping satisfying
be an even mapping satisfying  Assume that there exists a function
Assume that there exists a function  such that
such that


for all  Then there exists a unique generalized quadratic mapping of
Then there exists a unique generalized quadratic mapping of  -type
-type  such that
such that

for all 
Proof.
If  is replaced by
is replaced by  in the inequality (4.6), then the proof follows from the proof of Theorem 4.1.
in the inequality (4.6), then the proof follows from the proof of Theorem 4.1.
References
Ulam SM: Problems in Morden Mathematics. John Wiley & Sons, New York, NY, USA; 1960.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000,251(1):264–284. 10.1006/jmaa.2000.7046
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Applicandae Mathematicae 2000,62(1):23–130. 10.1023/A:1006499223572
Rassias ThM: The problem of S. M. Ulam for approximately multiplicative mappings. Journal of Mathematical Analysis and Applications 2000,246(2):352–378. 10.1006/jmaa.2000.6788
Skof F: Local properties and approximation of operators. Rendiconti del Seminario Matematico e Fisico di Milano 1983, 53: 113–129. 10.1007/BF02924890
Cholewa PW: Remarks on the stability of functional equations. Aequationes Mathematicae 1984,27(1–2):76–86.
Chu H-Y, Kang DS: On the stability of an
 -dimensional cubic functional equation. Journal of Mathematical Analysis and Applications 2007,325(1):595–607. 10.1016/j.jmaa.2006.02.003
-dimensional cubic functional equation. Journal of Mathematical Analysis and Applications 2007,325(1):595–607. 10.1016/j.jmaa.2006.02.003Forti GL: Hyers-Ulam stability of functional equations in several variables. Aequationes Mathematicae 1995,50(1–2):143–190. 10.1007/BF01831117
Forti G-L: Comments on the core of the direct method for proving Hyers-Ulam stability of functional equations. Journal of Mathematical Analysis and Applications 2004,295(1):127–133. 10.1016/j.jmaa.2004.03.011
Tabor J, Tabor J: General stability of functional equations of linear type. Journal of Mathematical Analysis and Applications 2007,328(1):192–200. 10.1016/j.jmaa.2006.05.022
Tabor J: Locally expanding mappings and hyperbolicity. Topological Methods in Nonlinear Analysis 2007,30(2):335–343.
Acknowledgment
The authors would like to thank the referee for his (or her) constructive comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lee, SH., Koh, H. & Ku, SH. Investigation of the Stability via Shadowing Property. J Inequal Appl 2009, 156167 (2009). https://doi.org/10.1155/2009/156167
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/156167



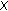 and
and 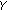 be Banach spaces with norms
be Banach spaces with norms 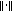 and
and  respectively. Hyers showed that if a function
respectively. Hyers showed that if a function  satisfies the following inequality:
satisfies the following inequality: -dimensional cubic functional equation. Journal of Mathematical Analysis and Applications 2007,325(1):595–607. 10.1016/j.jmaa.2006.02.003
-dimensional cubic functional equation. Journal of Mathematical Analysis and Applications 2007,325(1):595–607. 10.1016/j.jmaa.2006.02.003