1 Introduction

Synchronization stands out as a captivating phenomenon not only in real-world systems but also in the realms of computational mathematics and neuroscience [1]. It represents an impressive and crucial collective pattern, dependent on the interaction of two or more entities within a predetermined or time-varying structure. In essence, the exploration of synchronization requires the application of complex networks—graph-based structures comprising nodes and links [2]. In this context, the temporal evolution of nodes shapes the overall network dynamics, while the links define the configuration or structure of node connections [3]. Within complex networks, synchronization occurs when all or some nodes achieve a high level of coherency [1]. This definition encompasses a spectrum of collective dynamics. For instance, complete synchronization denotes full coherency among all nodes, signifying the network’s attainment of a unique solution [4]. When high-level coherency emerges in distinct clusters of interconnected nodes, it is termed cluster synchronization [5]. The chimera pattern represents another significant synchronization phenomenon, wherein a cluster with a low level of coherency coexists with a coherent cluster [6]. Additionally, phase synchronization and lag synchronization are renowned types of synchronization patterns. Phase synchronization occurs when coherency is observed in the phases of oscillations [7], while lag synchronization manifests in correlated delayed temporal evolutions [8]. These diverse synchronization patterns enrich our understanding of collective behaviors in complex systems.

In nonlinear dynamics, the study of neuronal models holds a distinct significance, given the crucial role of neuronal dynamics in various biological processes [9,10,11] or diseases [12, 13]. Consequently, these investigations are underpinned by robust foundations. Various neuronal models, including different versions of Hodgkin–Huxley [14,15,16], Hindmarsh–Rose (HR) [17,18,19], FitzHugh–Nagumo [20,21,22], Wilson [23, 24], Rulkov [25, 26], and Chialvo [27, 28] models. Such studies spanned over neuronal networks, and different neuronal models have been configured in a network structure to govern the dynamics of the network nodes [29, 30]. The synchronization of diverse neuronal models, whether flow-based or map-based, has been a focal point of extensive study in this field. However, many of these investigations incorporate simplifications, with a notable common assumption found in existing literature being the neglect of non-pairwise or multi-node interactions [31, 32]. Despite this simplification, higher-order interactions have been demonstrated to exist across a spectrum of systems, from biological and physical systems to social networks [33, 34]. Recognizing the significance of addressing these simplifications for a comprehensive understanding of synchronization dynamics, recent years have seen a shift towards considering networks with higher-order interactions. For example, in [35], the authors demonstrated that introducing non-pairwise couplings to the network can enhance synchronization. The study in [36] also revealed that synchronization patterns can be scaled to lower coupling strength by considering more nodes involved in multi-node connections, highlighting the impact of higher-order interactions. The synchronization of higher-order networks under different first- and second-order coupling functions was the subject of study in [37]. Furthermore, [38] investigated the effect of higher-order interactions on synchronization patterns, and [39] explored the synchronization of a higher-order network with a multilayer structure.

Time-varying networks represent another pivotal area of investigation, particularly in the context of neuronal networks where structures often exhibit time-dependent characteristics [40]. Within such time-varying networks, the connectivity structure [41] and/or the coupling functions [42] undergo temporal evolution. For instance, the synchronization of on–off or blinking network models has been examined in prior works [41, 43] across various network structures. The mathematical investigation of the effect of switching between different schemes on the synchronization state was conducted in [44]. Additionally, [42] demonstrated the influence of the blinking scheme on the synchronization state, while [45] provided evidence that the adaptive scheme of blinking coupling is effective in enhancing synchronization. This paper focuses on a higher-order network of HR systems featuring time-dependent on–off switching couplings, commonly referred to as blinking couplings. The study aims to examine the impact of blinking frequency and higher-order interactions on the synchronization state of the network. Sections II and III provide a detailed description of the network model and its synchronization stability analysis under scrutiny, while Section IV presents the study's results. The paper concludes in Section V, summarizing the key findings gleaned from the investigation.

2 Higher-order blinking model

Simplicial complexes are mathematical objects that can model higher-order interactions in networks [31]. Specifically, they comprise simplexes of various dimensions representing connectivity between nodes. An individual node is a 0-simplex. A link between two nodes forms a 1-simplex. Three connected nodes form a 2-simplex, capturing a triangle structure. More broadly, an \(n\)-simplex refers to a set of \(n+1\) nodes that are all connected in a specific way, and not all nodes are directly connected. By assembling simplexes of different dimensions, simplicial complexes can encode higher-order connectivity patterns beyond just pairwise links, generally known as non-pairwise interactions [31, 35]. For example, they can capture triangle structures and more complex motifs present in real-world data. As such, simplicial complexes provide a valuable framework for analyzing the rich, multi-node interactions in higher-order networks. This contrasts with standard network representations that only capture direct pairwise relationships.

Here, we consider that when each set of three nodes participates in a triangle topology, forming what is known as a 2-simplex, they possess a relationship that extends beyond pairwise connections. The mathematical definition of a simplicial complex of order \(d=2\) is as follows:

$${\dot{X}}_{i}=F\left({X}_{i}\right)+{\sigma }_{1}\sum_{j=1}^{N}{a}_{ij}^{\left(1\right)}{G}^{\left(1\right)}\left({X}_{i},{X}_{j}\right)+{\sigma }_{2}\sum_{j=1}^{N}\sum_{k=1}^{N}{a}_{ijk}^{\left(2\right)}{G}^{\left(2\right)}\left({X}_{i},{X}_{j},{X}_{k}\right),$$
(1)

where \({X}_{i}\) is a vector containing \(d\) state variables that describe the current condition of \(i\)-th node, while \(F\left({X}_{i}\right)\) is a vector function of \(d\) dimensions, with each component capturing the self-contained local dynamics of the \(i\)-th node. Also, \(N\) is the number of nodes and \({\sigma }_{1}\) and \({\sigma }_{2}\) are coupling parameters that quantify the interaction strengths between connected nodes in the system. Specifically, \({\sigma }_{1}\) denotes the weight of two-node links, with a higher value corresponding to a stronger pairwise connection. Meanwhile, \({\sigma }_{2}\) characterizes the intensity of three-node triangular couplings with a larger value of \({\sigma }_{2}\) indicating more heightened triadic interactions between triplets of nodes. The first- and second-order adjacency matrices/tensors \({A}^{\left(1\right)}={\left[{a}_{ij}^{\left(1\right)}\right]}_{N\times N}\) and \({A}^{\left(2\right)}={\left[{a}_{ijk}^{\left(2\right)}\right]}_{N\times N\times N}\) show the existence of links and triangles between two and three nodes, respectively. In other words, \({a}_{ij}^{\left(1\right)}=1\) shows that the nodes \(i\) and \(j\) are connected via a link while \({a}_{ijk}^{\left(2\right)}=1\) shows that nodes \(i\), \(j,\) and \(k\) participated in forming a triangular connection. \({a}_{ij}^{\left(1\right)}={a}_{ijk}^{\left(2\right)}=0\) also indicates no connection among the corresponding nodes. The coupling functions which determine the relation of two- and three-node interactions are specified with \({G}^{\left(1\right)}\left({X}_{i},{X}_{j}\right)\) and \({G}^{\left(2\right)}\left({X}_{i},{X}_{j},{X}_{k}\right)\), respectively. Figure 1 illustrates how network connectivity and dynamics are built up from individual nodes to paired to triplet interactions. Specifically, Figure 1a1 shows eight disconnected nodes, each with internal dynamics dictated by \(F({X}_{i})\). Figure 1a2 then introduces two-node links, coupling the isolated behaviors via pairwise connections weighted by the coupling parameter \({\sigma }_{1}\). Lastly, Fig. 1a3 demonstrates how three mutually connected nodes also coupled to each other in triangles, incorporating higher-order triadic interactions modulated by three-node coupling strength \({\sigma }_{2}\). Overall, the progression from Fig. 1a1–a3 demonstrates how the network model incrementally accounts for complex connectivity patterns (from zero links in fully decoupled nodes to direct node pairs and finally to triangular connections), ultimately allowing both two-node and three-node couplings to shape emergent dynamical behaviors.

Fig. 1
figure 1

Evolution from isolated nodes to higher-order networked systems. a1 Eight decoupled nodes (0-simplex), each with independent dynamics \({\text{F}}({{\text{X}}}_{{\text{i}}})\). a2 Conventional network with pairwise links (1-simplex) connecting the nodes. a3 Higher-order network with additional triangular connections (2-simplex), representing non-dyadic couplings among triplets of nodes

Full size image

The network described in Eq. (1) can be considered a static network since the structure and coupling functions are not time-dependable. However, in real-world systems, including biological ones, the networks are time-dependable [46]. To make the system time-dependable, we considered the structure fixed at each time instance, while the coupling function is blinking in each blinking period \(\tau\) or with the blinking frequency \(\frac{1}{\tau }\). Thus, Eq. (1) changes into the following network:

$${\dot{X}}_{i}=F\left({X}_{i}\right)+{\sigma }_{1}\sum_{j=1}^{N}{a}_{ij}^{\left(1\right)}H\left(t\right){G}_{ij}^{\left(1\right)}\left({X}_{i},{X}_{j}\right)+{\sigma }_{2}\sum_{j=1}^{N}\sum_{k=1}^{N}{a}_{ijk}^{\left(2\right)}H\left(t\right){G}_{ijk}^{\left(2\right)}\left({X}_{i},{X}_{j},{X}_{k}\right),$$
(2)

where \(H\left(t\right)\) is an \(d\times d\) time-varying coupling matrix that switches or blinks between variables according to the following relation:

$$\begin{aligned}{H}_{mm}\left(t\right)&=\left\{\begin{array}{c}\begin{array}{cc}1& {\text{for}}\frac{\left(m-1\right)\tau }{d}<t\le \frac{m\tau }{d}\end{array}\\ \begin{array}{cc}0& {\text{otherwise}}\end{array}\end{array},\right.\\{H}_{mn}\left(t\right)&=0,\\H\left(t+\tau \right)&=H\left(t\right),\end{aligned}$$
(3)

where \(m,n=\mathrm{1,2},\dots ,d\).

In this paper, to investigate the effect of pairwise and non-pairwise blinking couplings on the synchronization state of the network, we considered the dynamics of the three-dimensional HR system as the node’s dynamics, which is described according to the following equations:

$$\dot{X}=F\left(X\right)=\left\{\begin{array}{c}f\left(x,y,z\right)=y+3{x}^{2}-{x}^{3}-z+{I}_{ext},\\ g\left(x,y,z\right)=1-5{x}^{2}-y,\\ h\left(x,y,z\right)=r\left[s\left(x+1.6\right)-z\right],\end{array}\right.$$
(4)

where \(x\), \(y\), and \(z\) represent state variables that track key physiological processes in the neuron. Precisely, \(x\) reflects membrane potential changes, while \(y\) and \(z\) variables model faster and slower ion channel gating speeds underlying bursting patterns. \(r\) and \(s\) are the control parameters, and \({I}_{ext}\) is the current externally applied to the membrane potential. Figure 2 demonstrates the chaotic bursting spiking activity of the HR neuron model under the following settings: \(r=0.006\), \(s=4\), \({I}_{ext}=3.2\), and \(\left({x}_{0},{y}_{0},{z}_{0}\right)=\left(\mathrm{0.1,0},0\right)\).

Fig. 2
figure 2

The chaotic bursting behavior of the HR neuron: a1 The three-dimensional state space trajectory and a2 the time evolution of the state variables \(x\) (shown in red), \(y\) (shown in green), and \(z\) (shown in blue). The parameters are set at \(r=0.006\), \(s=4\), \({I}_{{\text{ext}}}=3.2\), and the initial condition is \(\left({x}_{0},{y}_{0},{z}_{0}\right)=\left(\mathrm{0.1,0},0\right)\)

Full size image

The forthcoming sections investigate synchronization phenomena in blinking higher-order networks composed of three globally coupled HR neuron models. Both analytical proofs and numerical simulations are supplied to demonstrate synchronization in these complex dynamical systems.

3 Stability analysis

Master stability functions (MSFs) provide a mathematically elegant framework for assessing synchronization stability in complex networks of coupled oscillators without explicitly calculating the full graph Laplacian spectrum [47]. The key insight is examining how small deviations from synchrony grow or decay over time. Specifically, the MSF probes the dynamics of a representative transverse perturbation mode, measuring the maximum Lyapunov exponent (MLE) of deviations. If MLE is negative across a continuous range of the coupling parameter, the synchronized state is stable.

To set up the analysis, we first posit that complete synchronization emerges over time, meaning all \(N\) neuronal state variables become identical across the network, obeying \({X}_{1}={X}_{2}=\dots = {X}_{N}=X\). This equivalence implies that the neurons are evolving in unison. Thus, the coupled network dynamics in Eq. (2) collapse exactly onto the isolated single-neuron model given by Eq. (4), becoming \(\dot{X}=F(X)\). To enable a tractable analysis, we first considered \(H\left(t\right)\) constant over time and \({H}_{mm}=1\). Moreover, the formulations of the coupling functions are assumed to be in linear diffusive forms given by \({G}^{\left(1\right)}\left({X}_{i},{X}_{j}\right)={X}_{j}-{X}_{i}\) and \({G}^{\left(2\right)}\left({X}_{i},{X}_{j},{X}_{k}\right)={X}_{j}+{X}_{k}-2{X}_{i}\). To analyze the stability of the synchronized state, we introduce small perturbations to the neuronal trajectories in the synchronous state. Specifically, we define a perturbation vector for each neuron as \(\delta {X}_{i}={X}_{i}-X\), which represents a small deviation of the state \({X}_{i}\) away from the synchronized state \(X\). Leveraging these definitions and assumptions, we can derive the equations governing the dynamics of the perturbation system according to the following equation:

$$\delta {\dot{X}}_{i}=DF\left(X\right)\delta {X}_{i}+{\sigma }_{1}\sum_{j=1}^{N}{a}_{ij}^{\left(1\right)}\left[{\left.\frac{\partial \left({X}_{j}-{X}_{i}\right)}{\partial {X}_{i}}\right|}_{\left(X,X\right)}\delta {X}_{i}+{\left.\frac{\partial \left({X}_{j}-{X}_{i}\right)}{\partial {X}_{j}}\right|}_{\left(X,X\right)}\delta {X}_{j}\right]+{\sigma }_{2}\sum_{j=1}^{N}\sum_{k=1}^{N}{a}_{ijk}^{\left(2\right)}\left[{\left.\frac{\partial \left({X}_{j}+{X}_{k}-2{X}_{i}\right)}{\partial {X}_{i}}\right|}_{\left(X,X,X\right)}\delta {X}_{i}+{\left.\frac{\partial \left({X}_{j}+{X}_{k}-2{X}_{i}\right)}{\partial {X}_{j}}\right|}_{\left(X,X,X\right)}\delta {X}_{j}+{\left.\frac{\partial \left({X}_{j}+{X}_{k}-2{X}_{i}\right)}{\partial {X}_{k}}\right|}_{\left(X,X,X\right)}\delta {X}_{k}\right],$$
(5)

which leads to the following equation:

$$\delta {\dot{X}}_{i}=DF\left(X\right)\delta {X}_{i}+{\sigma }_{1}\sum_{j=1}^{N}{a}_{ij}^{\left(1\right)}\left[\delta {X}_{j}-\delta {X}_{i}\right]+{\sigma }_{2}\sum_{j=1}^{N}\sum_{k=1}^{N}{a}_{ijk}^{\left(2\right)}\left[\delta {X}_{j}+\delta {X}_{k}-2\delta {X}_{i}\right].$$
(6)

The adjacency matrix \({A}^{\left(1\right)}\) can be rewritten as \({A}^{\left(1\right)}={P}^{\left(1\right)}-{L}^{\left(1\right)}\), where \({L}^{\left(1\right)}=\left\{\begin{array}{c}\begin{array}{cc}{p}_{i}^{\left(1\right)}& i=j\end{array}\\ \left\{\begin{array}{c}\begin{array}{cc}0& i\ne j {\text{ with }} {a}_{ij}^{\left(1\right)}=0\end{array}\\ \begin{array}{cc}-1& i\ne j {\text{ with }} {a}_{ij}^{\left(1\right)}=1\end{array}\end{array}\right.\end{array}\right.\) is the first-order Jacobian matrix with \({p}_{i}^{\left(1\right)}=\sum_{j=1}^{N}{a}_{ij}^{\left(1\right)}\) and \({P}^{\left(1\right)}\) is the diagonal matrix whose non-zero elements are the degree of the network nodes. Similarly, we have \({A}^{\left(2\right)}={P}^{\left(2\right)}-{L}^{\left(2\right)}\), where \({L}_{ij}^{\left(2\right)}=\left\{\begin{array}{c}\begin{array}{cc}2{p}_{i}^{\left(2\right)}& i=j\end{array}\\ \left\{\begin{array}{c}\begin{array}{cc}0& i\ne j {\text{ with }} {a}_{ij}^{\left(1\right)}=0\end{array}\\ \begin{array}{cc}-{p}_{ij}^{\left(2\right)}& i\ne j {\text{ with }} {a}_{ij}^{\left(1\right)}=1\end{array}\end{array}\right.\end{array}\right.\) and \({p}_{i}^{\left(2\right)}=\frac{1}{2}\sum_{j=1}^{N}\sum_{k=1}^{N}{a}_{ijk}^{\left(2\right)}\). This results in the following equation:

$$\delta {\dot{X}}_{i}=DF\left(X\right)\delta {X}_{i}-{\sigma }_{1}\sum_{j=1}^{N}{L}_{ij}^{\left(1\right)}\delta {X}_{j}-{\sigma }_{2}\sum_{j=1}^{N}\sum_{k=1}^{N}{L}_{ijk}^{\left(2\right)}\left[\delta {X}_{j}+\delta {X}_{k}\right].$$
(7)

Knowing the fact that \(\sum_{j=1}^{N}\delta {X}_{j}\sum_{k=1}^{N}{L}_{ijk}^{\left(2\right)}\delta {X}_{k}=\sum_{k=1}^{N}\delta {X}_{k}\sum_{j=1}^{N}{L}_{ijk}^{\left(2\right)}\delta {X}_{j}\), Eq. (7) can be changed into the below equation:

$$\delta {\dot{X}}_{i}=DF\left(X\right)\delta {X}_{i}-{\sigma }_{1}\sum_{j=1}^{N}{L}_{ij}^{\left(1\right)}\delta {X}_{j}-2{\sigma }_{2}\sum_{j=1}^{N}{L}_{ij}^{\left(2\right)}\delta {X}_{j}.$$
(8)

As declared in [48], in the complete network structure, \({L}^{\left(2\right)}=\left(N-2\right){L}^{\left(1\right)}\). Consequently we have:

$$\delta {\dot{X}}_{i}=DF\left(X\right)\delta {X}_{i}-\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right)\sum_{j=1}^{N}{L}_{ij}^{\left(1\right)}\delta {X}_{j}.$$
(9)

Finally, due to the diagonalizability of \(DF\left(X\right)\delta {X}_{i}\) and \({L}^{\left(1\right)}\), Eq. (9) can be projected to the following linearized system:

$${\dot{\eta }}_{i}=\left[DF\left(X\right)-\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right){\lambda }_{i}\right]{\eta }_{i},$$
(10)

where \(\eta =\left[{\eta }^{x},{\eta }^{y},{\eta }^{z}\right]\) is the state vector of the perturbation system and \({\lambda }_{i}\) are the eigenvalues of \({L}^{\left(1\right)}\). In a complete network structure, we have \({\lambda }_{1}=0\) and \({\lambda }_{2}=\dots ={\lambda }_{N}=N\). Equation (10) can be generalized to incorporate time-dependent coupling modulations by introducing a blinking coupling matrix \(H\left(t\right)\) instead of fixed coupling functions. This gives:

$${\dot{\eta }}_{i}=\left[DF\left(X\right)-N\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right)H(t)\right]{\eta }_{i}.$$
(11)

For more clarity, for a three-dimensional HR system, the blinking matrix \(H\left(t\right)\) can be defined as:

$$\begin{aligned}H\left(t\right)&=\left\{\begin{array}{c}\begin{array}{cc}\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]& 0<t\le \frac{1}{3}\tau \end{array}\\ \\ \begin{array}{cc}\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]& \frac{1}{3}\tau <t\le \frac{2}{3}\tau \end{array}\\ \\ \begin{array}{cc}\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]& \frac{2}{3}\tau <t\le \tau \end{array}\end{array},\right.\\H\left(t+\tau \right)&=H\left(t\right),\end{aligned}$$
(12)

As previously mentioned, the negative values of MLE of Eq. (11) provide necessary conditions for the higher-order HR network with blinking couplings. It should be noted that the blinking period \(\tau\) is considered the same and simultaneous for both pairwise and non-pairwise neuronal interactions.

4 Results

This section investigates synchronization in the higher-order HR neuronal network using both analytical analysis and numerical simulations. On the analytical front, Lyapunov exponents of the perturbation system are derived to ascertain stability conditions. Complementing this, numerical integration of the coupled neuronal equations quantifies synchronization error to confirm the emergence of coherence. Specifically, the level of synchronization is numerically evaluated by calculating the averaged deviation between all neuronal trajectories via the formula:

$$Error=\frac{1}{\left(T-{t}_{0}\right)\left(N-1\right)}\sum_{t={t}_{0}}^{T}\sum_{j=1}^{N}\Vert {X}_{j}\left(t\right)-{X}_{1}\left(t\right)\Vert ,$$
(13)

where \(Error\) is the averaged synchronization error calculated over \(T-{t}_{0}\) time window across \(N-1\) neurons, taking the first neuron as a reference. Here. \(T\) represents the total simulation time while \({t}_{0}\) signifies the onset of stable network temporal behavior following a sufficiently long transient period. The symbol \(\Vert .\Vert\) is the Euclidean norm function. Smaller values of \(Error\) imply stronger coherence of the neuronal oscillations, and \(Error=0\) indicates complete synchrony. In the following results, a network of \(N=3\) nodes is considered.

Figure 3 shows three diagrams corresponding to the average network wherein \({H}_{{\text{avg}}}\left(t\right)=\left[\begin{array}{ccc}1/3 & 0& 0\\ 0& 1/3& 0\\ 0& 0& 1/3\end{array}\right]\), for \(0<t\le T\) (constant over time). Figure 3a1 shows the MLE of the Eq. (11) using with \({H}_{{\text{avg}}}\left(t\right)\) as a function of \({\sigma }_{1}\) in the absence of triadic interactions (\({\sigma }_{2}=0\)). In this case, the neurons synchronize for \({\sigma }_{1}\ge 0.014\). Similarly, Fig. 3a2 demonstrates the MLE as a function \({\sigma }_{2}\) in the absence of the dyadic connections (\({\sigma }_{1}=0\)). In this scenario, the neurons achieve synchrony for \({\sigma }_{2}\ge 0.007\). In a more general case, Fig. 3a3 illustrates the MLE of the perturbation system of the average network with both pairwise and non-pairwise connections engaged. In all cases, a linear relation between the synchronous and asynchronous regions is observable. Moreover, it can be seen that the critical coupling parameter value becomes significantly reduced as three-node interactions are introduced to the network. This suggests that the synchronization patterns are scaled to lower coupling parameter values when the triangular connections get stronger.

Fig. 3
figure 3

The MLE of the perturbation system corresponding to the average network: a1 Only dyadic connections are included (\({\upsigma }_{2}=0\)), a2 only triadic connections are involved (\({\upsigma }_{1}=0\)), and a3 both dyadic and triadic connections are simultaneously considered

Full size image

This linear pattern of MLE observed in Fig. 3 is backed by mathematical proofs. For an average network, \({H}_{{\text{avg}}}\left(t\right)\) can be rewritten as \(\frac{1}{3}I\), where \(I\) is the identity matrix. Thus, the perturbation equation of the average network becomes:

$${\dot{\eta }}_{i}=\left[DF\left(X\right)-N\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right)H(t)\right]{\eta }_{i}=\left[DF\left(X\right)-\frac{1}{3}N\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right)I\right]{\eta }_{i}.$$
(14)

We can analyze the linear transition in the MLE diagrams by examining the perturbation system’s eigenvalues. Let \({\gamma }_{0}\) denote the eigenvalues of the Jacobian matrix \(DF\left(X\right)\) governing the uncoupled dynamics. When the coupling is introduced, the eigenvalues become \(\gamma ={\gamma }_{0}-\frac{1}{3}N\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right)\) by matrix perturbation theory. Since the MLE (\(\Lambda\)) relates directly to the real part of \(\gamma\) averaged over the system solution, we have:

$$\Lambda ={\Lambda }_{0}-\frac{1}{3}N\left({\sigma }_{1}+2\left(N-2\right){\sigma }_{2}\right),$$
(15)

where \({\Lambda }_{0}\) is the MLE of the uncoupled system. This demonstrates that introducing coupling shifts the MLE by an amount proportional to the coupling strengths \({\sigma }_{1}\) and \({\sigma }_{2}\). Accordingly, the linear MLE transitions in Fig. 3 follow \(\Lambda ={\Lambda }_{0}-{\sigma }_{1}\), \(\Lambda ={\Lambda }_{0}-2{\sigma }_{2}\), and \(\Lambda ={\Lambda }_{0}-\left({\sigma }_{1}+2{\sigma }_{2}\right)\) for the cases of pairwise [panel (a1)], triplet [panel (a2)], and mixed-coupling [panel (a3)], respectively.

Figure 4 illustrates the results of stability and synchronization error analyses conducted on dynamical networks with blinking couplings. The left panels show the MLE calculated per Eq. (11), while the right panels display the synchronization error from Eq. (2). These metrics are examined across various blinking periods τ in networks restricted to either pairwise interactions alone (first row, with \({\sigma }_{2}=0\)) or pure triangular connections alone (second row, with \({\sigma }_{1}=0\)). The synchronization error plots serve to confirm the insights extracted from the MLE diagrams. Five blinking periods are highlighted, with red, blue, green, magenta, and cyan corresponding to \(\tau\) values of 30, 6, 3, 0.3, and 0.03, respectively. A notable observation is a similarity in overall MLE patterns between the pairwise and non-pairwise networks. The curves share the same pattern when plotted against coupling strength, with the case of the non-pairwise interactions simply scaled to the lower strength of the coupling parameter. Additionally, as the blinking period shortens and connections blink at higher frequencies, the MLE trends gradually linearize toward the expected pattern for a static, non-blinking average network. The synchronization error data further supports these insights revealed via MLE analysis on the impact of connectivity patterns and blinking timescales.

Fig. 4
figure 4

Synchronization assessment of the blinking higher-order HR system: a1 The MLE of Eq. (11) and a2 the averaged synchronization error of Eq. (2) calculated in the absence of triadic connections (\({\upsigma }_{2}=0\)). b1 The MLE of Eq. (11) and b2 the averaged synchronization error of Eq. (2) calculated in the absence of dyadic connections (\({\upsigma }_{1}=0\)). The red, blue, green, magenta, and cyan diagrams are plotted considering \(\uptau =30, 6, 3, 0.3\) and \(0.03\), respectively

Full size image

Figure 5 meticulously investigates the stability of synchronized states across a comprehensive range of blinking periods \(\tau\) by calculating the MLE and synchronization error. Notably, while replacing conventional link-based connections with triangular interactions preserves the established synchronization patterns, it necessitates a reduction in coupling strength. This suggests that the network’s inherent capacity for synchronization remains unaffected, albeit requiring a lower coupling intensity to maintain coherence. Furthermore, the figure demonstrates an inverse relationship between the blinking period and the critical coupling strength for synchronization. As \(\tau\) diminishes, signifying faster-blinking frequencies, the critical coupling strength also exhibits a concomitant decrease.

Fig. 5
figure 5

Synchronization assessment of the blinking higher-order HR system concerning different values of \(\uptau\): a1 The MLE of Eq. (11) and a2 the averaged synchronization error of Eq. (2) calculated in the absence of triadic connections (\({\upsigma }_{2}=0\)). b1 The MLE of Eq. (11) and b2 the averaged synchronization error of Eq. (2) calculated in the absence of dyadic connections (\({\upsigma }_{1}=0\))

Full size image

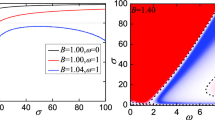
Figure 6 explores the behavior of the MLE of Eq. (11) as a function of both first- and second-order coupling strengths, considering scenarios where all links and triangular couplings blink simultaneously with identical period τ. Panel (a1) depicts the case for \(\tau =30\), with panels (a2) and (a3) progressively decreasing \(\tau\) to 3 and 0.03, respectively, representing increasingly faster-blinking rates. Notably, Fig. 6 reveals that while the synchronous and asynchronous regions maintain their linear separation pattern, the synchronous region consistently shrinks toward lower values of both coupling strengths. Furthermore, in the fastest blinking scenario [panel (a3)], the resulting MLE pattern mirrors that of Fig. 1a3, suggesting that as blinking speeds approach the limit (small enough value of \(\tau\)), the higher-order network converges toward the corresponding average network.

Fig. 6
figure 6

The MLE of Eq. (11) when both dyadic and triadic connections are involved for slow, moderate, and fast blinking couplings: a1 The blinking period is fixed as \(\uptau =30\) considered as slow blinking coupling, a2 The blinking period is fixed as \(\uptau =3\) considered as moderate blinking coupling, a3 The blinking period is fixed as \(\uptau =0.03\) considered as fast blinking coupling

Full size image

5 Conclusions

This study investigated the synchronization behavior of a higher-order (of order 2) neuronal network model with blinking couplings. We examined the influence of the first-order coupling parameter, second-order coupling parameter, and the blinking period on network dynamics. Prior findings in [42] established that for sufficiently rapid blinking frequencies, the network’s synchronizability converges to the behavior of an average network exhibiting a linear MSF pattern. Here, we extend this concept to higher-order networks. Through MSF analysis, we first demonstrate the linear pattern MLE of the average network’s perturbation system in three scenarios: (1) With only pairwise connections active, (2) with only non-pairwise interactions active, and (3) with both dyadic and triadic interactions simultaneously active. This comparative analysis facilitates the evaluation of the blinking higher-order network’s behavior against the benchmark of the average network. Furthermore, we elucidate how the linear MSF pattern manifests and changes in the presence of higher-order interactions. Subsequently, we conducted an MSF analysis of the blinking higher-order network across a spectrum of blinking speeds. Consistent with findings in [42], our results demonstrated that as blinking speeds increase, the network gradually converges towards the behavior of the average network. Notably, the presence of active higher-order couplings enhanced synchronization. We further revealed that incorporating non-pairwise connections scaled the synchronization patterns to lower coupling strengths compared to networks solely comprising pairwise interactions. In our presented study, we assumed that both the two- and three-node connections simultaneously adhere to the on–off coupling pattern. However, exploring the impact of distinct and non-simultaneous blinking periods could serve as a topic for future investigation.