Abstract
Simulating the von Neumann and second-order Rényi entropies of driven Mott insulators, we examine the entanglement dynamics of the \(\eta\)-pairing state in the one-dimensional half-filled Hubbard model after pulse irradiation. Corresponding data are obtained by means of the infinite time-evolving block decimation technique directly in the thermodynamic limit. For optimal pump-pulse parameters the temporal course of the entanglement entropies shows the characteristic entanglement growth due to the increase of \(\eta\)-pairing correlations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Off-diagonal long-range order plays a significant role in characterizing superconductivity in condensed matter systems, e.g., by the Meissner effect and the quantization of the magnetic flux [1]. The so-called \(\eta\)-pairing state, proposed by Yang for the paradigmatic Hubbard model several decades ago [2], possesses off-diagonal long-range order and recently attracted attention because it was noticed that optical pumping of Mott insulators may induce \(\eta\) pairs [3, 4]. There are several issues, however, in order to detect \(\eta\) pairing experimentally. First of all, the Hamiltonian should conserve the number of \(\eta\) pairs, which corresponds to a hidden SU(2) symmetry [5]. Although optical lattices might be promising candidates for implementing a Hubbard-model-like setup, in a following step, it is challenging to perform the time- and angle-resolved photoemission spectroscopy experiments necessary to prove such a photoinduced quantum phase transition [6].
Very helpful in this respect could be the analysis of entanglement properties. In the present theoretical study, we, therefore, focus on the discussion of the von Neumann entanglement entropy and the second-order Rényi entropy, which can be measured in optical lattices [7, 8]. Using the infinite time-evolved block decimation (iTEBD) technique [9] in the infinite matrix-product-state representation [10], these quantities can be calculated for the photoinduced \(\eta\)-pairing state of a one-dimensional (1D) electron system with short-range interaction directly in the thermodynamic limit.
2 Model
Our target system is the 1D Hubbard model at half filling
where \(t_{\textrm{h}}\) and U parametrize the nearest-neighbor particle hopping amplitude and the on-site Coulomb interaction, respectively. In Eq. (1), \(\hat{c}_{j,\sigma }^{\dagger }\) (\(\hat{c}_{j,\sigma }^{}\)) creates (annihilates) a spin-\(\sigma\) (\(=\uparrow ,\downarrow\)) electron at Wannier lattice site j, and \(\hat{n}_{j,\sigma }=\hat{c}_{j,\sigma }^{\dagger } \hat{c}_{j,\sigma }^{}\). We consider the repulsive case, so that the model realizes a Mott insulating ground state with a finite charge gap \(\Delta\) for any finite U.
Exact eigenstates of the Hubbard model can be constructed by means of the so-called \(\eta\) operators [2]
where \(\hat{\Delta }_j^\dagger =\hat{c}_{j,\downarrow }^\dagger \hat{c}_{j,\uparrow }^\dagger\) denotes the singlet electron-pair creation operator. The \(\eta\) operators fulfill SU(2) commutation relations \([\hat{\eta }^+,\hat{\eta }^-]=2\hat{\eta }^z\) and \([\hat{\eta }^z,\hat{\eta }^\pm ]=\pm \hat{\eta }^\pm\). It is worth noting that the Hubbard Hamiltonian (1) commutes with \(\hat{\eta }^2=\tfrac{1}{2}(\hat{\eta }^+\hat{\eta }^-+\hat{\eta }^-\hat{\eta }^+) + (\hat{\eta }^z)^2\), which implies that \(\langle \hat{\eta }^2 \rangle\) is a conserved quantity. While long-ranged pairing correlations \(\langle \hat{\eta }^+_j\hat{\eta }^-_{\ell }\rangle\) emerge when the expectation value \(\langle \hat{\eta }^2 \rangle /L^2\) becomes finite, with L being the number of sites, such \(\eta\)-paired states cannot be the ground state of the Hubbard model [2]. However, pulse irradiation can establish \(\eta\)-pairing in Mott insulators as demonstrated in Ref. [3].
To describe such a process, we consider a pump pulse with amplitude \(A_0\), frequency \(\omega _{\textrm{p}}\) and width \(\sigma _{\textrm{p}}\), centered at time \(t_0(>0\)):
With this, the hopping amplitude acquires a Peierls phase [11]: \(t_{\textrm{h}}\hat{c}_{j,\sigma }^\dagger \hat{c}_{j+1,\sigma }^{}\rightarrow t_{\textrm{h}}e^{\textrm{i}A(t)} \hat{c}_{j,\sigma }^\dagger \hat{c}_{j+1,\sigma }^{}\). As a result, the Hubbard Hamiltonian (1) becomes time-dependent \(\hat{H}\rightarrow \hat{H}(t)\) and the ground state at time \(t=0\) (\(|\psi (0)\rangle\)) is driven out of equilibrium as \(|\psi (0)\rangle \rightarrow |\psi (t)\rangle\).
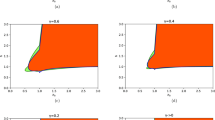
Contour plots of \(\tilde{P}(\pi ,t)\) (a) and \(2n_{\textrm{d}}(t)\) (b) in the \(\omega _{\textrm{p}}-A_0\) plane at time \(t=15t_{\textrm{h}}^{-1}\) for the irradiated 1D half-filled Hubbard model with \(U/t_{\textrm{h}}=8\). The pump pulse is parameterized by \(\sigma _{\textrm{p}}=2\) and \(t_0=10t_{\textrm{h}}^{-1}\)
3 \(\eta\)-pairing correlations
To detect the \(\eta\)-pairing state we compute the time evolution of the pair-correlation function
and its Fourier transform \(\tilde{P}(q,t)=\sum _r e^{\textrm{i}q r} P(r,t)\). Optical pumping will enhance \(\tilde{P}(\pi ,t)\), indicating the formation of \(\eta\) pairs, as first demonstrated for small clusters by exact diagonalization and TEBD [3, 12].
Figure 1a gives the contour plot of \(\tilde{P}(\pi ,t)\) after pulse irradiation at \(t=15t_{\textrm{h}}^{-1}\). \(\tilde{P}(\pi ,t)\) clearly shows a single maximum around \(A_0\approx 0.4\) and \(\omega _{\textrm{p}}/t_{\textrm{h}}\approx 7.0\) (marked in the figure by “+”), in contrast to the stripe structure observed in an exact-diagonalization calculation due to finite-size effects [3]. Furthermore, at large amplitudes \(A_0\), almost only the double occupancy \(n_{\textrm{d}}\) is enhanced noticeably after pulse irradiation as shown in Fig. 1b. Since the double occupancy is triggered by short-range correlations only, in this regime, the entanglement entropies should behave differently to the dominant \(\eta\)-pairing case characterized by longer-ranged correlations. In the following, we firstly compare the behavior of the entanglement entropies for the photoinduced \(\eta\)-pairing states with those away from the \(\eta\)-pairing dominated regime, \(A_0=0.4\) and \(\omega _{\textrm{p}}/t_{\textrm{h}}=4.0\) (marked as “x” in Fig. 1). Secondary, we will also study the behavior of the entropies at \(A_0=0.95\) and \(\omega _{\textrm{p}}/t_{\textrm{h}}=8.4\) (denoted as ‘\(\diamondsuit\)’), where \(n_{\textrm{d}}(t)\) exhibits a maximum, see Fig. 1b.
4 Entanglement entropies
Time dependence of the von Neumann (a and b) and second Rényi (c and d) entropies in the \(\eta\)-pairing non-dominant (a and c) with \(\omega _{\textrm{p}}/t_{\textrm{h}}=4.0\)] and dominant (b and d with \(\omega _{\textrm{p}}/t_{\textrm{h}}=7.0\)) regimes. Shown are iTEBD results for different bond dimensions \(\chi\) at \(U/t_{\textrm{h}}=8\). Pump parameters are \(A_0=0.4\), \(\sigma _{\textrm{p}}=2.0\) and \(t_0=10t_{\textrm{h}}^{-1}\)
Dividing the system into parts A and B, an entangled quantum state can be written as a Schmidt decomposition
where \(\chi\) is the Schmidt rank and \(|\lambda \rangle _{A,B}\) are orthonormal sets of states defined on the subsystems. Then the n-th Rényi entropy is defined as
where \(\hat{\rho }_A=\sum _\lambda |\lambda \rangle _A (s_\lambda )^2 _A\langle \lambda |\) is the diagonal reduced density matrix. The von Neumann entropy is obtained by taking the limit \(n\rightarrow 1\):
As is well known, the reduced density matrices of a half infinite chain (\(\rho _{A/B}\)) can be extracted from an infinite matrix-product-state representation of the state. Performing real-time evolutions by means of the iTEBD thus allows us to analyse the time-dependence of various entanglement entropies after pulse irradiation. In this context the second Rényi entropy is particularly relevant since it can be observed in optical-lattice experiments [7, 8].
Therefore, in the following, we will determine the time dependencies of the von Neumann [\(S_{\textrm{vN}}(t)\)] and second Rényi [\(S_{R}^2(t)\)] entropies, and discuss the characteristics of photoinduced \(\eta\)-pairing states in the 1D half-filled Hubbard model. Again, we fix the on-site Coulomb interaction to \(U/t_{\textrm{h}}=8\).
Figure 2a and b display our iTEBD results for the von Neumann entropy. In the absence of photoinduced \(\eta\) pairing, \(S_{\textrm{vN}}(t)\) shows only a very weak time dependence during the pump, see Fig. 2a with \(\omega _{\textrm{p}}/t_{\textrm{h}}=4.0\) marked as ’x’ in Fig. 1. As expected in this case, the data are almost independent of the bond dimension \(\chi\).
By contrast, at the \(\eta\)-pairing dominant point \(\omega _{\textrm{p}}/t_{\textrm{h}}=7.0\) marked as ’+’ in Fig. 1, the von Neumann entropy shows a noticeable increase during and shortly after the pulse irradiation and thereafter decreases for long times (\(t\gtrsim 20\)), see Fig. 2b. The increase of \(S_{\textrm{vN}}\) can be attributed to evolving long-ranged correlations of \(\eta\) pairs [2]. The subsequent decrease appears most likely because of an undersized bond dimension. Note that the linear increase of the entanglement entropy has also been observed after a sudden quench, see, e.g., Ref. [13].
Figure 2c and d indicate that the second Rényi entropy behaves almost the same as the von Neumann entropy: In the \(\eta\)-pairing non-dominant region, \(S_R^{(2)}(t)\) increases only slightly and a bond dimension \(\chi =1600\) is already sufficient, whereas we observe a strong dependence on the bond dimension in the \(\eta\)-pairing dominant regime.
Figure 3 gives the von Neumann and second Rényi entropies at the double-occupancy dominant point marked by a ‘\(\diamondsuit\)’ in Fig. 2. During the pump both \(S_{\textrm{vN}}(t)\) and \(S_R^{(2)}(t)\) show a pronounced upturn and, by contrast with Fig. 2, develop a clear plateau after pulse irradiation that can be related to short-range correlations in the doublon dominant states. Note, however, that the maximum values in Fig. 2 are smaller than those in Fig. 3 for the same bond dimensions. Therefore we need to inquire into the extent to which longer-ranged \(\eta\)-pairing correlations will enhance the maxima appearing in the entropies. To resolve this issue we have to perform calculations with larger bond dimensions which is beyond the means of our current computational resources, however.
5 Conclusions
To summarize, we demonstrated the entanglement growth due to the photoinduced \(\eta\)-pairing state for the one-dimensional Hubbard model at half band filling, utilizing unbiased numerical techniques that work in the thermodynamic limit. During and shortly after the pulse both the von Neumann entropy and the second Rényi entropy are enhanced almost linearly when optimal pump-pulse parameters for \(\eta\)-pairing are used. For doublon-dominant pump-pulse parameters the entanglement growth is also found. In this case, however, the entropy saturates immediately after pulse irradiation. We should once more like to reiterate that our theoretical findings, particularly for the Rényi entropy, should be observable in optical lattice experiments to detect \(\eta\) pairing.
Data availability
The datasets generated in this study are available from the corresponding author on reasonable request.
References
C.N. Yang, Concept of off-diagonal long-range order and the quantum phases of liquid he and of superconductors. Rev. Mod. Phys. 34, 694 (1962). https://doi.org/10.1103/RevModPhys.34.694
C.N. Yang, \(\eta\) pairing and off-diagonal long-range order in a Hubbard model. Phys. Rev. Lett. 63, 2144 (1989). https://doi.org/10.1103/PhysRevLett.63.2144
T. Kaneko, T. Shirakawa, S. Sorella, S. Yunoki, Photoinduced \(\eta\) pairing in the Hubbard model. Phys. Rev. Lett. 122, 077002 (2019). https://doi.org/10.1103/PhysRevLett.122.077002
S. Ejima, T. Kaneko, F. Lange, S. Yunoki, H. Fehske, Photoinduced \(\eta\)-pairing at finite temperatures. Phys. Rev. Res. 2, 032008 (2020). https://doi.org/10.1103/PhysRevResearch.2.032008
F.H.L. Eßler, Extended Hubbard models, eta-pairing and supersymmetry. J. Low Temp. Phys. 99, 415 (1995). https://doi.org/10.1007/BF00752318
S. Ejima, F. Lange, H. Fehske, Nonequilibrium dynamics in pumped Mott insulators. Phys. Rev. Res. 4, L012012 (2022). https://doi.org/10.1103/PhysRevResearch.4.L012012
R. Islam, R. Ma, P.M. Preiss, M. Eric Tai, A. Lukin, M. Rispoli, M. Greiner, Measuring entanglement entropy in a quantum many-body system. Nature 528, 77 (2015). https://doi.org/10.1038/nature15750
A.M. Kaufman, M.E. Tai, A. Lukin, M. Rispoli, R. Schittko, P.M. Preiss, M. Greiner, Quantum thermalization through entanglement in an isolated many-body system. Science 353, 794 (2016). https://doi.org/10.1126/science.aaf6725
G. Vidal, Classical simulation of infinite-size quantum lattice systems in one spatial dimension. Phys. Rev. Lett. 98, 070201 (2007). https://doi.org/10.1103/PhysRevLett.98.070201
R. Orús, G. Vidal, Infinite time-evolving block decimation algorithm beyond unitary evolution. Phys. Rev. B 78, 155117 (2008). https://doi.org/10.1103/PhysRevB.78.155117
R. Peierls, Zur Theorie des Diamagnetismus von Leitungselektronen. Z. Phys. 80(11), 763 (1933). https://doi.org/10.1007/BF01342591
S. Ejima, T. Kaneko, F. Lange, S. Yunoki, H. Fehske, Photoinduced \(\eta\)-pairing in one-dimensional Mott insulators. JPS Conf. Proc. 30, 011184 (2020). https://doi.org/10.7566/JPSCP.30.011184
P. Calabrese, J. Cardy, Evolution of entanglement entropy in one-dimensional systems. J. Stat. Mech. (2005). https://doi.org/10.1088/1742-5468/2005/04/P04010
M. Fishman, S.R. White, E.M. Stoudenmire, The ITensor software library for tensor network calculations. Sci. Post Phys. Codebases 5, 5 (2022). https://doi.org/10.21468/SciPostPhysCodeb.4
Acknowledgements
This project was made possible by the DLR Quantum Computing Initiative and the Federal Ministry for Economic Affairs and Climate Action; qci.dlr.de/projects/ALQU. The iTEBD simulations were performed using the ITensor library [14].
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ejima, S., Lange, F. & Fehske, H. Entanglement analysis of photoinduced \(\eta\)-pairing states. Eur. Phys. J. Spec. Top. 232, 3479–3482 (2023). https://doi.org/10.1140/epjs/s11734-023-00975-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjs/s11734-023-00975-6