1 Introduction

Wavenumber selection due to various forms of hydrodynamical shear instability is ubiquitous in nature. In the widely studied Couette–Taylor instability, for instance, periodic vortices emerge in the fluid between two parallel (or coaxial) rigid surfaces moving at different velocities [1, 2]. In the Kelvin–Helmholtz instability, velocity shear develops at the interface between two fluid layers of different densities and yields wavy disturbances if a critical threshold of velocity difference is surpassed [3, 4].

In domains with periodic boundaries (e.g. in flows in the azimuthal direction of a cylindrical or spherical system) the selection of “fastest growing” unstable wavenumbers can be further restricted by the condition that only integer multiples of the wavelength can fit along the circumference. Then the relationship \(k\cdot r = n\) (\(n=1;2;3;\ldots\)) between azimuthal wavenumber k and characteristic radius r must hold. Probably the most striking example for a flow created by an \(n=6\) shear instability is the enigmatic North Polar Hexagon of Saturn, a roughly 30,000 km-wide highly symmetric atmospheric pattern that was first noticed in images taken by the Voyager spacecraft [5]. There the shear between the zonal domains in the vicinity of the hexagon is maintained by the differential rotation of the gas giant planet [6].

A somewhat similar special case of shear instabilities has been reported relatively recently by Jansson et al. [7] in experiments using a cylindrical tank of fluid with fixed vertical sidewall and a bottom plate rotating rapidly at angular velocity \(\Omega _0\). In the viscous boundary layers the fluid must minimize its velocity relative to the rigid boundaries: it is forced to co-rotate with the horizontal plate, and to stay at rest in the vicinity of the static vertical walls, hence shear arises.

The considered experimental setting is a modified version of the well known textbook example of a rotating fluid surface, commonly referred to as “Newton’s bucket” [8], where all boundaries of a cylindrical cavity rotate at the same angular velocity \(\Omega _0\) around the vertical axis of symmetry, and the working fluid inside also exhibits solid body-like rotation. If, however, the sidewalls stay at rest but the bottom plate rotates, at certain values of \(\Omega _0\) (depending on the geometrical dimensions of the set-up and the viscosity of the working fluid) regular polygonal vortex-like drifting patterns appear at the free surface of the fluid.

The phenomenon has been studied in a handful of experimental and theoretical works [9,10,11] and, finally, [12, 13] have provided a clear and extensive framework (backed up by experiments) for the explanation of the underlying processes. The Tophøj model [12] treats the flow in this experiment as a perturbed, originally axially symmetric potential vortex. The selection of periodic modes is then facilitated by a resonant coupling of two different types of surface waves in the system, obeying different dispersion relations. Close to the nearly vertical water surface at the center of the cylinder, the flow is dominated by modes referred to as ‘centrifugal’, whereas gravity wave-like modes are excited simultaneously in the vicinity of the lateral walls. The interactions between these different branches of waves yield the amplification of certain perturbations of coalescent frequencies and wave numbers and the emergence of the polygonal patterns.

In the present work, we intended to test how far can one get with a decidedly simplistic “back-of-an-envelope” type of approach in determining the rotation rate of the polygons in the set-up, once knowing the wave numbers and the size of the dry area in the center, a posteriori. We find that a model based solely on an adjusted dispersion relation of small amplitude water surface (gravity) waves and a few simple assumptions regarding the velocity profile of the vortex gives fairly good, yet easy-to-obtain results for the angular velocities at which the polygon vortices propagate in the azimuthal direction.

Fig. 1
figure 1

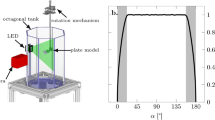
a The schematic layout of the experimental set-up and the position of the camera. b The cross-sectional sketch of the tank, showing the rotating axis connected to the roller bearing, to which the rotating plates of different diameters could be attached. The rabbets on the base for acrylic vertical cylinders of various diameters are also shown (not to scale)

Full size image

2 Set-up and methods

The basic layout of the set-up used for the experiments is depicted in Fig. 1. The runs were conducted in a 44.5 cm-wide cylindrical acrylic tank with an open top, mounted on a static stand. Tap water, colored with food dye for visualization was used as working fluid. The flow patterns were recorded by a simple off-the-shelf VGA digital camera (Trust Spotlight Pro webcam, 640px \(\times\) 480px, 25 fps) placed above the center of the tank so that the entire water surface stayed within its field of view (Fig. 1a).

A 7 cm-wide roller bearing was built in the center of the base plate, and rotating disks of different diameters could be attached to it with a screw, as sketched in the cross-sectional diagram in Fig. 1b. To adjust the width of the experimental cavity itself, cylindrical acrylic tubes of various diameters could be inserted into three concentric circular rabbets on the base plate (see Fig. 1b, not to scale). Hence—including the size of the tank itself—we were able to conduct experiments with five different values of cylinder diameter, namely \(D = (7.5;\, 14; \,17;\,27; \, 44.5)\) cm.

The rotating axis of the plate was connected to a turntable via transmission gears and a v-belt. The angular frequencies of the plate used in the experiments were in the interval of \(\Omega _0 =\) 8.2–50 rad/s and initial water height \(H_0\) was ranging from 1 cm to 7 cm.

\(\Omega _0\) was measured using a photogate placed underneath the tank, whose infrared light source was blocked once in each revolution by a small metallic flag attached to the axis of the plate. The turnaround times \(T_{{\textrm{lab}}}\) of the observed wave patterns (and their variances) with respect to the laboratory frame of reference—which were much longer than the period of the plate’s rotation—were measured directly from the video recordings.

3 Qualitative description of the flow

In this set-up the rotation of the bottom plate forces the fluid to co-rotate with it, similarly to the aforementioned case of “Newton’s bucket”, while the vertical cylindrical wall pulls the water body backwards at its sides, inducing shear. As viewed from the reference frame of the plate this sidewall drag appears to initiate a circular flow in the retrograde direction in the vicinity of the boundary. Small perturbations of the free fluid surface may then grow larger due to the positive feedback provided by Bernoulli’s principle: the cross section area of narrower domains of the annular streamtube tend to shrink further. These disturbances propagate around the cavity in the azimuthal direction as waves. However, due to the periodic boundary condition of the problem only such components of the perturbations get amplified sufficiently to become persistently observable which are in constructive interference with themselves, i.e. whose wavelengths fit integer times onto the circumference of the water surface.

Figure 2 shows typical examples of the observed regular wave patterns (for the parameters \(\Omega _0\), D, and \(H_0\) see the caption). In the top left panel the case of the \(n=0\) “base state” is visible, where the contact line between the (white) plate and the painted (dark) water surface is circular. The \(n=1\) case, corresponding to an elongated elliptical interface with the center of rotation close to one of its foci could be observed but only as a short-lived transient pattern during the spin-up of the system, therefore it could not be analyzed properly in the present work. Snapshots of the \(n=2;\,3;\,4\) patterns are visible in the further panels of Fig. 2. Regular waves with larger wavenumbers could not be observed in the technically accessible range of the experimental parameters \(\Omega _0\), D, and \(H_0\), except for a short transient appearance of an uncertain \(n=5\) pattern. It is to be noted that in the present study we decidedly do not discuss the nondimensional parameters which determine the observed value of n in the given experimental configuration: such regime diagrams have already been published and discussed in detail in, e.g. [9]. Instead, we take the observed and prescribed values of n, \(\Omega _0\), and the thickness of the fluid layer, and attempt to find a universal approximate relationship connecting these parameters with the observed drift rates.

Fig. 2
figure 2

Four typical examples of the observed shapes along the contact line between the fluid surface and the rotating plate. The experimental parameters were as follows: \(n = 0\): \(H_0 = 4\) cm, \(D = 17\) cm, \(\Omega _0 = 12.6\) rad/s; \(n = 2\): \(H_0 = 4.5\) cm, \(D = 17\) cm, \(\Omega _0 = 34.3\) rad/s; \(n = 3\): \(H_0 = 5\) cm, \(D = 44.5\) cm, \(\Omega _0 = 9.4\) rad/s; \(n = 4\): \(H_0 = 5\) cm, \(D = 44.5\) cm, \(\Omega _0 = 12.6\) rad/s.Contour lines (yellow) were added manually to highlight the fluid-plate interface (contact line)

Full size image

4 Quantitative theory

In our “simplistic” approach to estimate the drift rate of the polygonal patterns, we start from the idealized case of linear (small amplitude) gravity waves at the surface of a non-viscous fluid of uniform depth h. In such a setting the angular frequency \(\omega\) of a propagating wave, as detected by a stationary observer is determined by the well known dispersion relation

$$\begin{aligned}{} & {} \omega = \sqrt{g k \tanh (kh)}, \end{aligned}$$
(1)

where g denotes the acceleration of gravity, and k represents the wavenumber [14].

Although the formula (1) is not expected to be directly applicable for the large amplitude waves in question, it may still provide appropriate order-of-magnitude estimates of the drift rates with which the observations can be compared. Thus, our basic hypothesis—that the drifting polygons can actually be considered as gravity waves in a very special geometry—can be put to a test.

However, to comply with the boundary conditions of the studied configuration, Eq. (1) must be slightly adjusted. The angular frequency \(\omega _{\textrm{lab}}\) associated with wave propagation, as observed from the laboratory, is given by \(\omega _{\textrm{lab}} = 2\pi n / T_{\textrm{lab}}\), where \(n = 2;3;4\) is the number of “sides” of the observed polygons, and period \(T_{\textrm{lab}}\) is the time it takes for the drifting pattern to complete one full revolution with respect to the laboratory frame of reference. (Note, that \(\omega _{\textrm{lab}}\) is therefore not the angular velocity of the pattern, but an integer multiple of that.)

Let us assume now that we observe the wave propagation from a reference frame co-rotating with the bottom plate. Then the observed angular frequency \(\omega _{\textrm{wave}}\) of the wave is “Doppler shifted” so that \(\omega _{\textrm{wave}} = \omega _{\textrm{lab}}-\Omega _0\) holds, where \(\Omega _0\) denotes the angular velocity of the rotating plate. The wave number k in (1) is connected to n, and the average radial distance \(\bar{r}\) of the contact line between the fluid and the plate, measured from the axis of rotation as \(k=n/\bar{r}\).

In this rotating frame of reference centrifugal acceleration \(\vec {a}_{\textrm{cf}}\) must also be taken into account. Using \(\vec {\bar{r}}\) as a position vector pointing to an arbitrary point along a circle of characteristic radius \(\bar{r}\), \(\vec {a}_{\textrm{cf}}\) in the domain reads as \(\vec {a}_{\textrm{cf}}=v^{2}(\bar{r})/\bar{r}\cdot \vec {\bar{r}}/\bar{r}\)

Therefore g in (1) is to be replaced with the modulus of the vector sum of (downward pointing) \(\vec {g}\) and (“outward” pointing) \(\vec {a}_{\textrm{cf}}\), i.e. \(g' = \sqrt{a_{\textrm{cf}}^{2} + g^{2}}\), hereafter referred to as “modified gravity”. Accordingly, water depth h in the dispersion relation must also be replaced by the typical thickness \(h'\) of the water layer in the direction of \(\vec {g'}\). Due to the peculiarities of the setup’s geometry, even in the absence of a wave-like perturbations this thickness \(h'\) varies largely with the distance from the center. (A few examples of the local thickness measured in the direction of \(\vec {g'}\) are marked in the right-hand side cross section of the water body in Fig. 1b.) Also, this total “depth” at each point is changing markedly with the phase of the drifting polygonal pattern as sketched in the left-hand side of Fig. 1b with a dashed line. We found that taking \(h' \approx R-\bar{r}\), where R is the radius of the plate provides a consistent and easy-to-measure (upper) limit that can be used as a characteristic depth scale parameter in the system. Note, that via \(\bar{r}\) this quantity also depends on \(H_0\).

Thus, we can estimate a theoretical angular frequency of the wave propagation using the prescribed and observed values of \(\Omega _0\), n and \(\bar{r}\) as parameters to calculate the adjusted dispersion relation

$$\begin{aligned}{} & {} \omega _{\textrm{theor}} = \sqrt{g' k \tanh \left( k h'\right) }, \end{aligned}$$
(2)

and then to contrast the result with the observed \(\omega _{\textrm{wave}}\).

Fig. 3
figure 3

a The shape of the surface funnel of a vortex, generated by a stirrer rod (cf. [16]) in a steady cylindrical tank. The outline of the surface depression and the domain of parabolic shape (indicating solid body rotation) are marked with dotted and dashed lines, respectively. b Dye injected into the funnel, tracing out the material holding (no-shear) domain of the vortex. c An exemplary \(m=2\) polygonal vortex with a “wet” interior. d The schematic geometry of the typical cross-section surface shape z(r) in the experiments, with the average contact line distance \(\bar{r}\) and the inflection distance \(\xi\) marked, as measured from the axis of rotation and symmetry (dashed vertical line)

Full size image

It is to be noted that to estimate \(g'\) along the unperturbed contact circle one must know (or assume) the form v(r) of the tangential velocity profile. In the classic “Newton’s bucket” configuration the water body is in solid body rotation, implying \(v(r) = \Omega _0 r\) at all distances. However, [12, 13, 15] have demonstrated that in the set-up studied here the observed shape of the outer regions of the water surface is consistent with the assumption of a potential vortex characterized by tangential velocity that is inversely proportional to r outside a finite vortex core in the center.

Generally, as viewed from the co-rotating frame of reference the unperturbed (axially symmetric) water surface shape z(r) is set by the equilibrium between the (hydrostatic) pressure gradient force and the centrifugal force, and is given by

$$\begin{aligned}{} & {} \frac{v^2(r)}{r}=g\frac{\partial z(r)}{\partial r}. \end{aligned}$$
(3)

For the case of a rotating free-surface fluid in solid body rotation (Newton’s bucket), Eq. (3) yields the well-known parabolic shape

$$\begin{aligned}{} & {} z(r) = z_0 + \frac{\Omega _0^2 r^2}{2g}, \end{aligned}$$
(4)

where \(z_0\) is the water level at the center and g denotes the acceleration of gravity. \(z_0\) is determined by the radius R of the tank, the height \(H_0\) of the water at rest (i.e. in the same tank, without rotation) and \(\Omega _0\) as

$$\begin{aligned}{} & {} z_0 = H_0 - \frac{\Omega _0^2 R^2}{4g}. \end{aligned}$$
(5)

In case of \(z_0 < 0\), a “dry” domain appears around the center, and a circular contact line forms between the bottom plate and the surface of the working fluid. The condition for such an interface to appear is

$$\begin{aligned}{} & {} \Omega _0 > \frac{2}{R} \sqrt{gH_0}. \end{aligned}$$
(6)

In a potential vortex \(v(r)=k\cdot r^{-1}\), where k is a constant, however, the surface shape from (3) takes a form [12, 13]

$$\begin{aligned}{} & {} z(r)=\frac{k^2}{2g}\left( C-\frac{1}{r^2}\right) , \end{aligned}$$
(7)

where the integration constant C is set by \(H_0\), R, and k.

Earlier experiments on three dimensional vortices generated by a magnetic stirrer bar [16,17,18] in a fixed cylindrical tank of water have shown that the shape of the water surface can be approximated with the assumption that the flow is solid body-like in a domain \(r\le \xi\) around the center, and behaves like a potential vortex in the outer region \(r > \xi\). The continuous velocity profile—known as Rankine vortex [19]—can thus be written as

$$\begin{aligned}{} & {} v(r)={\left\{ \begin{array}{ll} \Omega _0 r, &{} \text {if}\quad r\le \xi .\\ \Omega _0 \xi ^2 /r , &{} \text {if}\quad r > \xi . \end{array}\right. } \end{aligned}$$
(8)

The surface shape corresponding to a Rankine vortex is, therefore, parabolic in the \(r\le \xi\) domain, and follows an inverse quadratic form (7) for \(r>\xi\). From (3) it then follows that the distance \(\xi\) can be practically detected as the inflection point as the surface shape z(r). Such a fluid surface of a stirrer bar-generated vortex from a control experiment—where the depression was far above the bottom of the tank—is shown in Fig. 3a. The funnel is highlighted by a dotted line and the radial boundaries of the parabolic domain of width \(2\xi\) are marked with dashed lines. Fig. 3b demonstrates that food dye, injected into the funnel with a syringe does not propagate beyond this domain of solid body rotation. Here no shear arises that would mix the dye and dilute it rapidly (as it would happen in the potential vortex-like region).

The relevance of the v(r) profile for the problem studied here lies in whether the unperturbed average contact radius \(\bar{r}\) of the “dry” area is smaller or larger than the parameter \(\xi\) of the Rankine vortex. If \(\bar{r}\le \xi\) holds, i.e. the contact line lies in the parabolic domain, so the shape of the fluid surface has an observable inflection at distance \(\xi\), as sketched in Fig. 3d–then the centrifugal acceleration at \(\bar{r}\) in the formula of \(g'\) can be written as \(a_{\textrm{cf}} = \Omega _0^2 \bar{r}\). The case of \(\xi < \bar{r}\), however, means that the intersection curve (contact line) of the bottom plate and the Rankine vortex lies outside of the (then) hypothetical distance of inflection. Then \(a_{\textrm{cf}} = \Omega _0^2 \xi ^4 \bar{r}^{-3}\) is to be applied.

The fact that in certain experiments we could clearly observe the appearance of the polygonal patterns even when the center domain was not dry (as also reported by, e.g., [10]) indicates that \(\bar{r}>\xi\) cannot be a necessary condition for the occurrence of the instability. Such a “wet” \(m = 2\) pattern is shown in Fig. 3c, where the reflections of light from the water layer in the center are clearly visible. We note, however, that we restricted our quantitative analysis to experiments in which the center was dry, as this markedly simplified the visual observation and evaluation of the patterns.

Based on the above reasoning and the visual observation of the water surface shape, we concluded that it is not far-fetched to assume that in the vicinity of the circular contact line the unperturbed flow exhibits approximate solid body rotation, and hence \(g' = \sqrt{\Omega _0^4 \bar{r}^2 + g^2}\) can be used in the adjusted dispersion relation for the description of the waves formed by the displacement of this contact line (2).

5 Results

Fig. 4
figure 4

Scatter plot of the measured angular frequencies of the polygonal waves with respect to the frame of reference co-rotating with the plate \(\omega _{\textrm{wave}}\) as a function of the calculated “theoretical” angular frequency \(\omega _{\textrm{theor}}\). The diameter D of the tank and the mode number n is indicated in the legend. Different data points with the same n and D differ in \(\Omega _0\) and \(H_0\). The dotted line represents the \(\omega _{\textrm{wave}}=0.42\,\omega _{\textrm{theor}}\) linear trend line. The inset shows the data points from the experiments contrasted with nondimensionalized dispersion relations from different small-amplitude theories: linear long-wave limit (black dotted line), linear short-wave limit (blue dashed line), linear “full” dispersion (red solid line), and the nonlinear BBM theory’s small-amplitude limit (green solid curve)

Full size image

Our findings are summarized in Fig. 4, where the measured values of angular frequency \(\omega _{\textrm{wave}}\) are plotted against the theoretical approximation \(\omega _{\textrm{theor}}\) for all tank diameters, wavenumbers, rotation rates and initial heights combined.

The length of the vertical error bars represent the double standard deviation of the observed (but not precisely constant) angular frequency of the polygonal pattern in a given experiment. The horizontal error bars originate from the uncertainty of the estimated characteristic water thickness \(h'\): as mentioned above, for the calculations \(h' \approx R-\bar{r}\) was used, which includes the mean radius \(\bar{r}\) of the contact line. We repeated the same calculation with the minimum and maximum radial distance of the contact line in the given pattern as “depth” scales, and the resulting values are represented by the endpoints of each horizontal interval.

Apparently, the scatter plot shows a manifest correlation and a fairly good data collapse around the fitted linear trend line \(\omega _{\textrm{wave}}=0.42(\pm 0.02)\,\omega _{\textrm{theor}}\) implying that the theoretical framework based on the dispersion relation of inviscid, small amplitude surface waves above a uniform bottom topography provides an acceptable order-of-magnitude estimate for the observed propagation when adjusted with an empirical form factor of 0.4.

6 Discussion and conclusions

In the present work we addressed the problem of drifting regular wave patterns (also referred to as “polygon vortices”) on the free water surface of a cylindrical shear flow. We argue that the wavelengths and angular frequencies of these disturbances appear to be consistent with the hypothesis that the observed propagation can be interpreted as gravity waves travelling along the tilted water surface.

It is important to emphasize, however, that the formula (2) was not expected to properly describe the actual waves in the experiment, which clearly do not fulfill the initial assumptions of the model: the fluid is not inviscid (otherwise shear, the driving mechanism of the instability could not even take place), the amplitudes are not small compared to the effective water thickness \(h'\), and \(h'\) is not uniform. Yet, the fact that the formula yields a fairly good collapse of experimental data from very different geometries (Fig. 4)—even if not along the \(y=x\) line—does indicate that the basic underlying assumption of gravity wave propagation holds.

In the \(kh'\ll 1\) (long-wave) limit the phase velocity \(c=\omega /k\) from (2) reduces to the non-dispersive relationship \(c_0 = \sqrt{g'h'}\), whereas the \(kh'\gg 1\) (short-wave) approximation yields \(c_{\textrm{sw}}=\sqrt{g'/k}\). The question may then arise of whether, and to what extent the observed wave dynamics can be described in terms of these limits. The inset of Fig. 4 shows the nondimensional (observed) phase velocities \(c/c_0\) of the polygonal waves from all set-ups as a function of their relative wavenumber \(kh'\). When expressed with these variables the long-wave approximation (\(c=c_0\)) is represented by a constant (black dashed) line at unity, the short-wave limit follows the \(1/\sqrt{x}\) hyperbola (blue dashed curve). The full dispersion relation of the linear theory is marked by the solid red curve. The data points scatter below the theoretical curves—as expected from the aforementioned results—but nevertheless exhibit a clear decreasing trend. This, and the fact that they are all located in the \(kh'>1\) domain indicate that the long-wave approximation is inadequate, but it is also visible that in this interval the short-wave limit already gives practically the same (over-) estimate as the full formula.

As mentioned earlier, the selection of \(h'\) in this configuration is somewhat arbitrary, and is therefore clearly a source of uncertainty. This fact is also expressed by the horizontal error bars in Fig. 4, whose endpoints correspond to alternative definitions of \(h'\), where—instead of its average distance \(\bar{r}\)—the minimum and maximum radii of the contact line was considered in determining \(h'\). Taking the lower limit of this interval for each experiment would only increase the slope of the linear fit from 0.42 to 0.47. For the data points to reach the \(y=x\) line in the main panel of Fig. 4—or the nondimensional phase velocity curve in the inset—a completely unrealistic value of \(h'\) would be required. Therefore, we can state that this mismatch cannot be solely blamed on the problem of \(h'\) selection, but nonlinear effects may also be taken into account.

Periodic solutions of the weakly nonlinear Korteweg–de Vries (KdV) wave equation [14] and its improved version, the Benjamin–Bona–Mahony (BBM) equation [20] (exhibiting better short-wave behaviour) are referred to as cnoidal waves, which propagate at the following wave speed:

$$\begin{aligned}{} & {} c=c_0\left[ 1+\frac{H}{m h'}\left( 1-\frac{1}{2}m-\frac{3}{2}\frac{E(m)}{K(m)}\right) \right] , \end{aligned}$$
(9)

where, as before, \(c_0=\sqrt{g'h'}\), H marks the wave height (the difference between crest and trough elevation), and K(m) and E(m) are the complete elliptic integrals of the first and second kind, respectively. The elliptic parameter \(0<m<1\) of the solution also determines the shape of the waves via the \(\textrm{cn}(m)\) Jacobi elliptic function (hence the name “cnoidal”). The waveform for \(m=0\) corresponds to sinusoidal waves, whereas the \(m=1\) limit represents non-periodic solitary wave solutions. For \(m < 0.82\) the velocity is below the linear long-wave limit (\(c<c_0\)) and decreases with the decreasing m [21].

The phase speed in the limit of infinitesimal wave height can be derived from the BBM cnoidal solution’s formula for wavelength \(\lambda (H/m; c; h'; K(m))\), from which H/m can be obtained and substituted into (9), yielding a function \(c(\lambda ; h'; m; E(m); K(m))\), which can then be expressed with k as well, since \(k=2\pi /\lambda\). Taking the first-order Taylor series expansions of K(m) and E(m) [22], one gets a \(c(kh')\) relation in the nonlinear small-amplitude limit which reads as

$$\begin{aligned}{} & {} c=\frac{c_0}{1+\frac{1}{6}\left( kh'\right) ^2}. \end{aligned}$$
(10)

Comparing this formula—shown with a green solid curve in the inset of Fig. 4—to the experimental data points we find a manifestly better agreement than in the case of linear wave theories, despite the fact that (10) does not take wave amplitudes into account either. This observation implies that the effect of nonlinearity in the dynamics of the polygonal waves may contribute more to the 0.42 correction factor than the uncertainty of the depth scale \(h'\).