1 Introduction

The human faced various troubles based on different viruses and diseases all the time. Some common viruses/diseases that are dangerous and troublesome for the humanity are Ebola, HIV and dengue, and most recent disease is coronavirus [1,2,3]. The dangerous coronavirus is communicated disease that has an effective part in the lives of the humans since 2020. It seriously affected the industrial zones, economic factors, sports activities, social actions, education fields and other events [4, 5]. This virus is harmful, spreading rapidly with the huge casualties occurred in quick time. The effective coronavirus spreading role is due to transportations or travel of people through the flawed countries of various sectors [6, 7]. The procedure of the vaccination has been started that is helpful to control this virus. The coronavirus changed the human’s life and the basic reason of the spreading of this disease is the migration of the individual from one to another place; however, few more reasons and symptoms have also been reported [8].

There have been several schemes that have been applied to present the mathematical formulations based on the coronavirus together with various topographies. Benvenuto et al. [9] executed the nonlinear ARIMA model based on the coronavirus. Rhodes et al. [10] studied the communal sufferings-based coronavirus using the mathematical ODEs. Mustafa et al. [11] designed a mathematical formulation to analyze and forecast the transmission of coronavirus. Nesteruk [12] evaluated the dynamical form of the coronavirus in Ukraine based on the double set of data. Sivakumar [13] discussed the predictive measures to control the pandemic coronavirus in the region of India. Thompson [14] investigated the epidemiological model by using the momentous apparatus based on the coronavirus interventions. Libotte [15] designed an administration strategy using the vaccination process of the coronavirus. Gumel et al. [16] presented a mathematical coronavirus disease nonlinear system. Sadiq et al. [17] examined the of nanomaterial impacts to control the coronavirus. Ortenzi et al. [18] implemented an investigation using the transdisciplinary discipline for this disease in Italy. Moore et al. [19] investigated a nonlinear system of coronavirus to examine the impacts of the vaccination along with the non-pharmaceutical interference. Sánchez et al. [20] proposed a SITR coronavirus mathematical model that is based on susceptible/infected/treatment/recovered system. Sabir et al. [21] designed the stochastic computing numerical procedure using the coronavirus SITR system. Umar et al. [22] provided the theoretical presentations to present the dynamical structure of the coronavirus. Chen et al. [23] show the effects of social distancing using the nonlinear form based on the coronavirus dynamics. Anirudh [24] investigated the dynamical structure of the transmission prediction of the coronavirus. Zhang et al. [25] stated the coronavirus studies using the performances of the perturbation stochastic factor.

The current investigations present the fractional derivative investigation based on the susceptibility/infected/quarantine, i.e., SIQ system based on the lockdown impacts of the coronavirus using the artificial intelligence (AI) performances along with the scale conjugate gradient (SCG) design, i.e., AI-SCG. The stochastic solvers have been used in the variety of applications in recent years [26,27,28]. Few of them are the singular model of third kind [29], nonlinear functional differential model [30] and singular kinds of fractional systems [31, 32]. However, these intelligent computing frameworks have yet to implement on fractional SIQ system considering the lockdown impacts on spread of coronavirus. Authors are motivated to investigate/explore in AI-SCG algorithms for fractional SIQ systems for the first time as per our literature review. The novel features of the AI-SCG scheme for the SIQ differential model are given as:

  • A fractional SIQ system of coronavirus with the impact of lockdown is numerically studied.

  • The stochastic computing procedure-based AI-SCG scheme has not been implemented before for solving the fractional SIQ nonlinear mathematical system.

  • Three fractional-order variations of the fractional SIQ coronavirus system have been numerical discussed, which validate the trustworthiness of the AI-SCG scheme.

  • The competency of the computing stochastic AI-SCG scheme is observed by using the comparative performances of the achieved and Adam results.

  • The accuracy/correctness and precision of the AI-SCG solver is observed based on the performances of the absolute error (AE), which is obtained in good order for solving the model.

  • The error histograms (EHs) performances, state transitions (STs) measures, correlation/regression values and mean square error (MSE) approve the reliability of the AI-SCG procedure for the fractional SIQ nonlinear mathematical system.

The other sections of this paper are presented as: The construction of the fractional SIQ system is shown in 2nd Sect. The computing AI-SCG process is studied in 3rd Sect. The numerical results based on the fractional SIQ system are reported in 4th Sect. In the final section, concluding remarks of this study are presented.

2 System model: fractional SIQ nonlinear model

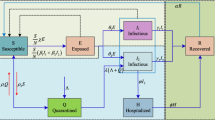
The current section presents the effects of the lockdown in the protective analysis of the SIQ system. The impact of the lockdown is classified into the susceptible/infections/quarantine categories, which is based on the system of differential models. The mathematical nonlinear SIQ system along with the initial conditions (ICs) is given as [33]:

$$\left\{ \begin{array}{l@{\quad}l} \frac{dS(v)}{{dv}} = (1 - \theta )m + a - \mu S(v)\\ \qquad - \frac{\beta S(v)I(v)}{{\alpha + \eta I(v)}}, & S_{0} = l_{1} , \hfill \\ \frac{dI(v)}{{dv}} = \frac{\beta (1 - k)S(v)I(v)}{{\eta I(v) + \alpha }} + \theta m \\ \qquad - (\delta_{1} + \alpha_{1} + \sigma + \mu )I(v), & I_{0} = l_{2} , \hfill \\ \frac{dQ(v)}{{dv}} = \frac{k\beta I(v)S(v)}{{\eta I(v) + \alpha }} \\ \qquad+ \sigma I(v) - (\mu + \alpha_{2} + \delta_{2} )Q(v), & Q_{0} = l_{3} . \hfill \\ \end{array} \right.$$
(1)

The exhaustive/necessary descriptions of terms/variables/parameters of the mathematical SIQ nonlinear system are presented in Table 1. Furthermore, the appropriate values of terms/variables/parameters have been selected as shown/reported in [33] together with the theoretical descriptions of the optimal control for necessary description global/local stabilities approaches.

Table 1 Comprehensive descriptions of each class of the nonlinear SIQ mathematical system
Full size table

The present work shows the computing numerical performance of the fractional SIQ nonlinear system-based lockdown effects of coronavirus by using the artificial intelligence (AI) performances along with the SCG-based neural networks design. The modified form of the model (1) is presented as:

$$\left\{ \begin{array}{l@{\quad}l} \frac{{d^{\eta } S(v)}}{{dv^{\eta } }} = (1 - \theta )m + a - \mu S(v) \\ \qquad- \frac{\beta S(v)I(v)}{{\alpha + \eta I(v)}}, & S_{0} = l_{1} , \hfill \\ \frac{{d^{\eta } I(v)}}{{dv^{\eta } }} = \frac{\beta (1 - k)S(v)I(v)}{{\eta I(v) + \alpha }} + \theta m \\ \qquad- (\delta_{1} + \alpha_{1} + \sigma + \mu )I(v), & I_{0} = l_{2} , \hfill \\ \frac{{d^{\eta } Q(v)}}{{dv^{\eta } }} = \frac{k\beta I(v)S(v)}{{\eta I(v) + \alpha }} \\ \qquad+ \sigma I(v) - (\mu + \alpha_{2} + \delta_{2} )Q(v), & Q_{0} = l_{3} . \hfill \\ \end{array} \right.$$
(2)

where \(\eta\) represents the fraction0order Caputo derivative form of the SIQ nonlinear system. The values of the fractional derivative have been applied in the interval [0, 1] to present the conduct of the dynamical SIQ nonlinear model.

The advantages of the fractional SIQ model presented in system (2) are incorporated to signify/observe the minute particulars (superfast/ superslow transients/evolutions) that are not easy to handle by using the classical integer order counterparts as presented in the system (1). However, inherent complexity of the fractional SIQ model in (2) is a limitation of the presented study due to availability of relatively few numerical and analytical procedures for solving fractional-order systems as portrayed in (2). Therefore, the aim of the presented study is to utilize the knacks of artificial intelligence performances along with the scale conjugate gradient design, i.e., AI-SCG, to analyze the dynamics of fractional-order system represented in set of Eq. (2).

3 Methodology: proposed AI-SCG procedure

This section shows the AI-SCG structure for the fractional SIQ dynamical system. The procedure is defined by using the important AI-SCG performances along with the execution measures using the AI-SCG scheme for solving the SIQ dynamical model. The designed AI-SCG scheme is implemented with the similar study as presented in [34, 35].

The procedure based on the optimization of the multilayers based on the stochastic numerical AI-SCG is presented in Fig. 1. The neuron structure-based single layer is presented in Fig. 2. The regression-based knacks of AI-SCG-based supervised neural networks are incorporated to study the dynamics of fractional SIQ system while reference dataset for the implementation of the regressive networks is formulated using Adams numerical procedures for the solution of fractional differential equations [36,37,38]. The statics to perform the numerical results of the fractional SIQ dynamical system are 7% for validation, 82% for training and 11% for testing.

Fig. 1
figure 1

Workflow illustrations-based AI-SCG-based neural networks for the fractional SIQ system

Full size image
Fig. 2
figure 2

A single-layered neuron structure

Full size image

4 Numerical results based on AI-SCG neural networks with discussion

The current section presents the numerical computing performances of three variations based on the fractional-order derivatives of the SIQ system by applying the AI- SCG-based neural networks. The three cases of fractional SIQ systems are formulated by taking the values of terms/variables/parameters as shown/reported in [33] for not only in-depth analysis of dynamic of the model but also to check the accuracy, robustness, stability and convergence of the proposed AI-SCG neural networks. The mathematical description of these three cases are given as follows:


Case 1: Consider \(\eta = 0.5,\) \(\beta = 2.1,\) \(\alpha = 5,\) \(a = 2.6,\) \(\sigma = 0.59\), \(\alpha_{1} = 1.78\), \(\eta = 1\), \(\delta_{1} = 0.4\), \(\alpha_{2} = 1.78\), \(\mu = 5.2,\)\(\delta_{2} = 0.4\), \(k = 0.1\), \(\theta = 0.9\), \(m = 14\), \(l_{1} = 1.32\), \(l_{2} = 2.29\) and \(l_{3} = 3.5\) is given as:

$$\left\{ \begin{array}{l@{\quad}l} \frac{{d^{0.5} S(v)}}{{dv^{0.5} }} = 4 - 5.2S(v)\\ \qquad - \frac{2.1S(v)I(v)}{{5 + I(v)}}, & S(0) = 1.32, \hfill \\ \frac{{d^{0.5} I(v)}}{{dv^{0.5} }} = 12.6 - 7.97I(v) \\ \qquad+ \frac{1.89I(v)S(v)}{{I(v) + 5}}, & I(0) = 2.29, \hfill \\ \frac{{d^{0.5} Q(v)}}{{dv^{0.5} }} = 0.59I(v)\\ \qquad + \frac{0.21S(v)I(v)}{{5 + I(v)}} - 7.38Q(v), & Q(0) = 3.5. \hfill \\ \end{array} \right.$$
(3)

Case 2: Consider \(\eta = 0.5,\) \(\beta = 2.1,\) \(\alpha = 5,\) \(a = 2.6,\) \(\sigma = 0.59\), \(\alpha_{1} = 1.78\), \(\eta = 1\), \(\delta_{1} = 0.4\), \(\alpha_{2} = 1.78\), \(\mu = 5.2,\)\(\delta_{2} = 0.4\), \(k = 0.1\), \(\theta = 0.9\), \(m = 14\), \(l_{1} = 1.32\), \(l_{2} = 2.29\) and \(l_{3} = 3.5\) is shown as:

$$\left\{ \begin{array}{l@{\quad}l} \frac{{d^{0.7} S(v)}}{{dv^{0.7} }} = 4 - 5.2S(v) \\ \qquad- \frac{2.1S(v)I(v)}{{5 + I(v)}}, & S(0) = 1.32, \hfill \\ \frac{{d^{0.7} I(v)}}{{dv^{0.7} }} = 12.6 - 7.97I(v) \\ \qquad+ \frac{1.89I(v)S(v)}{{I(v) + 5}}, & I(0) = 2.29, \hfill \\ \frac{{d^{0.7} Q(v)}}{{dv^{0.7} }} = 0.59I(v) \\ \qquad+ \frac{0.21S(v)I(v)}{{5 + I(v)}} - 7.38Q(v), & Q(0) = 3.5. \hfill \\ \end{array} \right.$$
(4)

Case 3: Consider \(\eta = 0.5,\) \(\beta = 2.1,\) \(\alpha = 5,\) \(a = 2.6,\) \(\sigma = 0.59\), \(\alpha_{1} = 1.78\), \(\eta = 1\), \(\delta_{1} = 0.4\), \(\alpha_{2} = 1.78\), \(\mu = 5.2,\)\(\delta_{2} = 0.4\), \(k = 0.1\), \(\theta = 0.9\), \(m = 14\), \(l_{1} = 1.32\), \(l_{2} = 2.29\) and \(l_{3} = 3.5\) is provided as:

$$\left\{ \begin{array}{l@{\quad}l} \frac{{d^{0.9} S(v)}}{{dv^{0.9} }} = 4 - 5.2S(v) \\ \qquad- \frac{2.1S(v)I(v)}{{5 + I(v)}}, & S(0) = 1.32, \hfill \\ \frac{{d^{0.9} I(v)}}{{dv^{0.9} }} = 12.6 - 7.97I(v)\\ \qquad + \frac{1.89I(v)S(v)}{{I(v) + 5}}, & I(0) = 2.29, \hfill \\ \frac{{d^{0.9} Q(v)}}{{dv^{0.9} }} = 0.59I(v)\\ \qquad + \frac{0.21S(v)I(v)}{{5 + I(v)}} - 7.38Q(v), & Q(0) = 3.5. \hfill \\ \end{array} \right.$$
(5)

Figure 3 shows the structure of the input/hidden/output layers for the fractional SIQ nonlinear dynamical model using the AI-SCG solver.

Fig. 3
figure 3

Neuron structure for the fractional SIQ system

Full size image

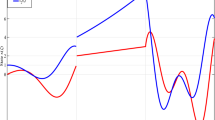
The graphical illustrations are provided in Figs. 4, 5, 6 for the fractional SIQ system by using the AI-SCG scheme. To authenticate the optimal measures and STs values, the graphical plots are drawn in Figs. 4, 5. Figure 4 shows the MSE values and STs for the verification, training and best curves to present the solutions of the fractional SIQ mathematical model. The achieved MSE measures for the optimal performances based on the fractional SIQ dynamical system have been illustrated at epoch 1000 for 1st and 3rd case, while for the 2nd case the epoch has been counted as 474. The MSE values for the 1st, 2nd and 3rd case are 9.80 × 10–09, 2.26 × 10–08 and 4.25 × 10–09. The 2nd part of Fig. 4 shows the gradient measures for the fractional SIQ dynamical system by using the AI-SCG procedure, which are performed as 1.00 × 10–08, 1.00 × 10–08 and 1.00 × 10–08 for case 1, 2 and 3. The convergence of the scheme is observed through these graphical plots for presenting the solutions of the fractional SIQ mathematical system. The fitting curves performances are illustrated in Figs. 5, 6, 7 and 8 for each variation of the fractional SIQ dynamical system. These illustrations indicate the comparative presentations of the achieved and database reference solutions. The illustrations based on the error are drawn in Fig. 5 (a to c) using the training, substantiation and testing measures to present the numerical solutions of the fractional SIQ mathematical system, whereas the EHs plots are drawn in Fig. 5d–f that are calculated as − 7.7 × 10–06, − 1.2 × 10–05 and − 1.6 × 10–05 for case 1–3. Figure 6a–c presents the regression measures for solving the fractional SIQ dynamical system. Figure 6 indicates the regression performance through the correlation measures. It is observed that the correlation values are found as 1 to solve the mathematical fractional SIQ dynamical system. The correctness is observed through the performances based on the substantiation/training/testing procedures indicating the exactness of the stochastic AI-SCG solver for the mathematical fractional SIQ dynamical system. The convergence operator performances using the MSE measures based on the backpropagation, verification, complexity, training, Epoch and testing are presented in Table 2 for the mathematical fractional SIQ dynamical system. The comprehensive details of the parameters presented as; the authentication measures show the fitness performances, i.e., MSE, means the data samples applied to the authentication, i.e., 7% in total samples, Mu shows the adaptive scale conjugate gradient parameter based on the controlling convergence algorithm coefficient, performance represents the MSE fitness, gradient shows the 1st kind of optimal parameter, and complexity in 2nd shows the amendment of the networks.

Fig. 4
figure 4

MSE analysis and STs values for the fractional SIQ nonlinear system

Full size image
Fig. 5
figure 5

Result assessments and EHs for the fractional SIQ nonlinear system

Full size image
Fig. 6
figure 6

Regression illustrations for the fractional SIQ nonlinear system

Full size image
Fig. 7
figure 7

Result comparisons for the fractional SIQ nonlinear system

Full size image
Fig. 8
figure 8

AE for the fractional SIQ nonlinear system

Full size image
Table 2 Stochastic performance for the fractional SIQ nonlinear system
Full size table

Figures 7 and 8 present the comparison of the results along with the AE. These numerical illustrations have been drawn for the mathematical fractional SIQ dynamical system using the stochastic performances of the AI-SCG procedure. The performances based on the reference as well as obtained solutions are drawn in Fig. 7 that have been provided by using the matching of the solutions. The overlapping of the solutions validates the correctness of the AI-SCG scheme to present the mathematical fractional SIQ dynamical system. The values of the AE for the dynamical SIQ system are illustrated in Fig. 8. The AE measures based on the susceptible individuals S(v) performed as 10–04 to 10–05, 10–04 to 10–06 and 10–05 to 10–06 for 1st to 3rd case. These values for the infected individuals I(v) drawn as 10–04 to 10–06, 10–04 to 10–05 and 10–05 to 10–06 for respective cases of the system. Likewise, the AE values-based quarantine individuals Q(v) performed as 10–05 to 10–06, 10–03 to 10–04 and 10–04 to 10–06. These illustration-based AE indicate the correctness of the AI-SCG solver to present the numerical solutions of the fractional SIQ dynamical system.

5 Conclusion

The motive of this study is to present the computing numerical procedures based on the fractional mathematical susceptible/infected/quarantine, i.e., a SIQ system of the lockdown impacts using the coronavirus. The fractional-order investigations have been used to provide precise solutions of the SIQ dynamical system. The investigations based on the integer and nonlinear based on the mathematical SIQ dynamical system together with the effects of lockdown have also been presented. The lockdown impacts are classified into the susceptible/infections/quarantine categories, which is based on the system of differential models. The fractional investigations have been illustrated to investigate the precise as well as accurate solutions of the SIQ system using the artificial intelligence procedure together with the scale conjugate gradient design. Three cases based on the fractional-order derivatives have been presented to solve the nonlinear SIQ differential model. The statics to perform the numerical results of the fractional SIQ dynamical system have been provided as 7% for validation, 82% for training and 11% for testing. To observe the exactness of the AI-SCG procedure, the comparison of the numerical attained performances of the results has been presented with the reference Adam solutions. For the validation, authentication, aptitude, consistency and validity of the AI-SCG solver, the computing numerical solutions have been authenticated based on the state transition measures, error histograms, correlation/regression performances as well as mean square error.

In upcoming studies, the procedure AI-SCG solver can be executed to present the numerical performances of the nonlinear system, biological models as well as computer virus models.