1 Introduction

There is a huge demand on new sources of renewable energies. On the one hand, new types of autonomous systems, for example autonomous sensors in the ocean, need an energy source in order to be able to operate autonomously. For this, renewable sources of energy supplied by the environment of these systems are most desirable. On the other hand, it is desirable to develop new sources of renewable energy for powering devices or regions which do not have access to a power grid, such as ocean platforms or small islands. Of course, power generated from harvesting emission free renewable energy sources, such as wind or ocean waves, will lead to a better climate. There is ongoing research on new concepts of wave energy converters [1,2,3,4], since theoretically wave energy has a power density of 9.42 kW/m\(^2\) in comparison to wind and solar energy, which have a power density of 0.58 and 0.17 kW/m\(^2\) [5], respectively. However, there are still big challenges in wave energy harvesting, since up to now only a very small amount of energy is harvested from ocean waves. This lies in the fact that ocean waves are highly irregular and produce only low frequency forcing, which makes it difficult to use standard generators for electrical energy production.

A well known wave energy converter (WEC) type is the so called point absorber. Generally, point absorbers are devices which possess small dimensions relative to the wavelength of the incoming waves. They can be of floating structure type which heaves up and down at the wave surface, see for example [6]. Other designs are submerged below the water surface, excited by the pressure difference. One example is the Arichemedes Wave Swing, cf. [7]. In comparison to other types of wave energy converters like attenuators or terminators, point absorbers have the advantage that due to their small size, the wave direction is not important [8]. Moreover, point absorbers differ in the number of moving components from which energy can be extracted. In the first generation, point absorbers have been constructed by using a single-body which oscillates in heave. Examples for this type can be seen in [6, 9]. Thereby, it has been shown that these devices can only harvest the maximal amount of energy if the natural frequency of the oscillating body corresponds to the frequency of the incoming waves [10,11,12], which is a serious disadvantage. Since the typical incident frequencies are usually very low (0.1–0.2 Hz), the dimensions of the mechanical system have to be impractically large, cf. [13]. Therefore, two-body WECs have been constructed, whereby an additional body is designed beneath the floating body [14, 15]. Energy can then be harvested from the relative heave motion of the two bodies. The second body can be used to improve the performance of the whole system. Nevertheless, Wu et al. [16] have found that the performance of a two-body wave energy converter highly depends on the parameters of the system and the incoming waves. Therefore, finding good system parameters is challenging.

Fig. 1
figure 1

Experimental rig in the wave flume of the Institute of Mechanics and Ocean Engineering from two different perspectives (a, b) and a sketch of the resulting wave energy converter (c)

Full size image

As a result of this difficult task of finding good parameters for two-body WECs, this work analyzes possible improvements of a single-body point absorber based WEC. Since a point absorber oscillating only in heave motion has a natural frequency higher than the frequencies of the incident water waves, the possibility of enhancing the magnitude of wave energy harvested by means of a guided inclined point absorber is investigated. In this way, forces in the travelling direction of the water waves can excite the WEC as well, which may lead to higher corresponding displacements. The considered point absorber consists of a cylindrical floating body (CFB), which is floating in regular and irregular water waves. Thereby, the irregular wave elevation is considered to be a non-white Gaussian random process. Such modeling is frequently used for real sea states, e.g. [17].

The content of this work is as follows: First, the modeling of the corresponding fluid structure interaction is presented in Sect. 2. Then, experimental results of the point absorber in a wave flume are shown for different setups in Sect. 3. Based on the experimental results and parameters, simulations for different setups of the considered point absorber are computed to analyze the corresponding energy harvesting performance in Sect. 4. Then, a simple control strategy for the increase of wave energy harvesting performance is proposed in Sect. 5. Finally, this work ends with a conclusion in Sect. 6.

2 Modeling of a wave energy converter excited by water waves

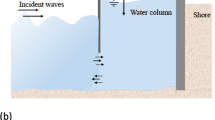
A wave energy converter, which consists of a single cylindrical buoy moving along a guidance, is considered. Figure 1a, b show a corresponding experimental rig in the wave flume of the Institute of Mechanics and Ocean Engineering from two different angles. It mainly consists of the CFB and an electrical generator. The CFB moves along the guidance rods with the displacement u in a plane, which is inclined by the adjustable angle \(\alpha \). A large dynamical response of the CFB due to incoming waves is desirable. From this guided linear motion, electrical energy can be harvested using the electrical generator. This wave energy converter type is known as a point absorber. There are different power take off systems, which convert linear motion to electrical energy, cf. [18]. Some of them convert the linear motion of a point absorber to rotary motion, which is for example described in [19].

The CFB has a radius of R and a draft of d. The water depth is denoted by H and the coordinate system (x, y, z) is located at the water surface in the absence of wave elevation \(\eta (x,z,t)\), whereby t denotes time. A sketch of the resulting system is shown in Fig. 1c.

In order to analyze the dynamical behavior of the considered wave energy converter forced by regular or irregular water waves, we first derive the corresponding equations of motion. For this, we determine the respective hydrodynamic forces by means of linear potential theory.

2.1 Equation of motion of the mechanical system

Considering the motion of the CFB in the inclined direction u, the corresponding equation of motion is given by

$$\begin{aligned} m{\ddot{u}}&=\cos (\alpha ) \int _S p(x,y,z,t) n_1 d S+\sin (\alpha ) \nonumber \\&\quad \biggl \lbrace \int _S p(x,y,z,t) n_2 d S-mg-{\sin (\alpha )} \lambda _{vis ,y}{\dot{u}} \biggl \rbrace \nonumber \\&\quad -F_d({\dot{u}}). \end{aligned}$$
(1)

Here, m is the mass of the CFB and the guiding rods; S is the wetted surface of the CFB; \(n_1\) and \(n_2\) are the normal vector in the x- and y-direction, pointing out of the fluid; g is the acceleration due to gravity; \(F_d({\dot{u}})\) is the velocity dependent damping force accounting from mechanical friction effects; \(\lambda _{vis ,y}\) is the viscous damping in the y-direction resulting from the fluid, as described in [20]. Thereby, we assume that in horizontal direction the water flows around the hull of the cylinder without any viscous damping, such that no viscous damping forces act in the x-direction.

Assuming an irrotational, unsteady flow, the pressure p can be computed by means of potential flow theory and Bernoulli’s equation [21] as follows:

$$\begin{aligned} p(x,y,z,t)=-\rho \frac{\partial \varPhi (x,y,z,t)}{\partial t}-\rho gy. \end{aligned}$$
(2)

Thereby, \(\varPhi \) is the velocity potential and \(\rho \) is the density of water. In Eq. (2), a linearization in \(\varPhi \) has been carried out. For incoming harmonic waves with wave amplitude A and frequency \(\omega \), the sea surface displacement is given by

$$\begin{aligned} \eta (x,t)=Re \lbrace A\exp (\mathrm {i}(k_{e }x-\omega t)) \rbrace . \end{aligned}$$
(3)

The wave number \(k_e\) can be computed by the dispersion relation

$$\begin{aligned} \omega ^2=k_{\text {e}}g\tanh (k_{e }H), \end{aligned}$$
(4)

where H is the water depth, see Fig. 1c. The corresponding velocity potential \(\varPhi \) can be written in the following form:

$$\begin{aligned} \begin{aligned}&\varPhi (x,y,z,t)=Re \lbrace A[\phi _0(x,y,z)+\phi _7(x,y,z)]\exp (-\mathrm {i}\omega t)\\&\quad +(-\mathrm {i}\omega )({\mathcal {A}}_1\varphi _{1}(x,y,z)+{\mathcal {A}}_2\varphi _{2}(x,y,z))\exp (-\mathrm {i}\omega t)\rbrace . \end{aligned} \end{aligned}$$
(5)

In this equation, \(\phi _0\) is the incident potential of the incoming wave; \(\phi _7\) is the scattering potential representing the reflections of the incident waves with respect to a non-moving CFB; \(\varphi _{1}\) and \(\varphi _{2}\) are the radiation potentials, which represent the velocity potential of rigid body motion with unit amplitude in x- and y-direction in the absence of incident waves, respectively; \({\mathcal {A}}_1\) and \({\mathcal {A}}_2\) are the respective complex amplitudes of the horizontal and vertical motion of the CFB. The excitation force in the x- and y-direction is defined by

$$\begin{aligned} f_x:=\mathrm {i}\omega \rho \int _{S}[\phi _0+\phi _7]n_1d S,~~ f_y:=\mathrm {i}\omega \rho \int _{S}[\phi _0+\phi _7]n_2d S. \end{aligned}$$
(6)

The added mass coefficients \(\mu _{j,k}\) and hydrodynamic damping coefficients \(\lambda _{j,k}\) in direction j resulting from a motion in direction k are defined by

$$\begin{aligned}&\mu _{j,k}+\mathrm {i}\frac{\lambda _{j,k}}{\omega }:=\rho \int _{S}\varphi _{k}n_j d S~\text {with}~\mu _{j,k},\lambda _{j,k}\in {\mathbb {R}}\nonumber \\&\quad ~\text {for} ~j,k\in \{ 1,2\}. \end{aligned}$$
(7)

Then, the equation of motion for the CFB in the direction u can be written as

$$\begin{aligned}&(m+c^2\mu _{1,1}+s^2\mu _{2,2})\ddot{u}\nonumber \\&\quad +(c^2\lambda _{1,1}+s^2\lambda _{2,2}+s^{{2}} \lambda _{vis ,y}){\dot{u}}\nonumber \\&\quad + F_d({\dot{u}}) +s^2\rho g \pi R^2 u=Re \lbrace A(c f_x+sf_y)e ^{-\mathrm {i}\omega t)}\rbrace .\nonumber \\ \end{aligned}$$
(8)

Here and in the following we use the abbreviations

$$\begin{aligned} s:=\sin (\alpha ), ~ c:=\cos (\alpha ). \end{aligned}$$
(9)

Moreover, the balance of forces in y-direction in the absence of water waves has been applied, which results in

$$\begin{aligned} \int _S \rho g y n_2\,d S=mg. \end{aligned}$$
(10)

It has to be noted that \(f_x\), \(f_y\), \(\mu _{j,k}\) and \(\lambda _{j,k}\) depend on the geometry of the system, wave frequency \(\omega \) and the water depth H, respectively. The values of \(f_x\), \(f_y\), \(\mu _{j,k}\) and \(\lambda _{j,k}\) can be computed by a matched eigenfunction method. The way of computation of the corresponding values is presented by Yeung in [22] and by Garrett in [23], respectively. In this study, a general nonlinear damping force \(F_d\) of the form

$$\begin{aligned} F_d({\dot{u}})=d_1 {\dot{u}}+d_2 | {\dot{u}}| {\dot{u}}+d_3 {\dot{u}}^3 \end{aligned}$$
(11)

is used, whereby the coefficients \(d_1\), \(d_2\) and \(d_3\) are determined by means of free decay tests.

2.2 Response amplitude operator

After transient motion has decayed, the dynamical behavior of a linear mechanical system excited by harmonic forcing becomes periodic. In order to harvest as much energy as possible, the velocity of the CFB has to be high. Therefore, the behavior of the amplitude of the CFB motion for different frequencies is of interest. This can be analyzed by introducing the response amplitude operator (RAO). For harmonic waves, the RAO is defined by the quotient of the amplitude of the incoming waves and the response amplitude of the CFB. For a linear damping force \(F_d ({\dot{u}})=d_lin {\dot{u}}\) and constant hydrodynamic coefficients, the motion of the CFB becomes harmonic with complex response amplitude \({\mathcal {A}}\):

$$\begin{aligned} u(t)=Re \lbrace {\mathcal {A}}e ^{-\mathrm {i}\omega t)}\rbrace . \end{aligned}$$
(12)

Therefore, the RAO is defined as the quotient of \({\mathcal {A}}\) and A, resulting in

$$\begin{aligned}&RAO(\omega ) =\frac{(c f_x+sf_y)}{s^2\rho g \pi R^2-\omega ^2(m+c^2\mu _{1,1}+s^2\mu _{2,2})-\mathrm {i}\omega (d_lin +c^2\lambda _{1,1}+s^2\lambda _{2,2}+s^{{2}}\lambda _{vis ,y})}. \end{aligned}$$
(13)

The corresponding \(RAO_{v}\) for the velocity is given by

$$\begin{aligned} RAO_{v}(\omega )=\frac{-\mathrm {i}\omega (c f_x+sf_y)}{s^2\rho g \pi R^2-\omega ^2(m+c^2\mu _{1,1}+s^2\mu _{2,2})-\mathrm {i}\omega (d_lin +c^2\lambda _{1,1}+s^2\lambda _{2,2}+s^{{2}}\lambda _{vis ,y})}.\qquad \end{aligned}$$
(14)

2.3 Modeling of irregular seas

In order to simulate a realistic sea surface, the superposition principle of harmonic waves is used. For a given harmonic wave with frequency \(\omega \) and wave number \(k_e(\omega )\), the wave amplitude is obtained from the corresponding one-sided spectral density \(S(\omega )\) [17, 24]. Then, the irregular long-crested sea surface can be computed by

$$\begin{aligned} Z(x,t)=\int _0^\infty \cos (\omega t - k_{e }(\omega ) x + \varepsilon (\omega )) \sqrt{2S(\omega ) d \omega },\nonumber \\ \end{aligned}$$
(15)

whereby the random phase shift \(\varepsilon (\omega )\) is equally distributed in the interval \([0,2\pi ]\). It has to be noted that the integral in Eq. (15) is not a Riemann integral, but a summation rule with respect to \(\omega \).

Common sea-spectra are the Pierson–Moskowitz spectrum for deep water and the Joint North Sea Wave Project (JONSWAP) spectrum for shallow water seas [25]. Both can be described by the modal frequency \(\omega _M\) and significant wave height \(H_s\). In this work, a modal frequency of \(\omega _M=1\,rad/s \) and significant wave height of \(H_s=2\,m \) is used in the following.

2.4 Simulation of system response in irregular waves

Equation (8) describes the motion of the CFB in regular waves. In order to extend this model to irregular seas consisting of many harmonic waves as given in Eq. (15), the equation of motion (8) has to be modified. An ansatz of computing the motion of a floating system in an irregular sea is to use average values for the added mass and hydrodynamic damping coefficients and include the excitation forces at the right hand side of Eq. (8), cf. [26]. Hence, in this work this ansatz is followed and constant frequency independent values for \(\mu _{j,j}\), \(\lambda _{j,j}\), \(j \in \lbrace 1,2 \rbrace \) are used. The excitation forces \(f_x\) and \(f_y\) are computed for each incoming harmonic component individually. For a given sea spectrum with prescribed modal frequency, \(\mu _{j,j}\) and \(\lambda _{j,j}\) are computed at \(\omega =\omega _M\). In this way, the response of water waves with frequency \(\omega _M\), which have the highest amplitude in the irregular sea, can be computed. Defining

$$\begin{aligned} {\bar{\mu }}_{j,j}:=\mu _{j,j}(\omega _M), ~~ {\bar{\lambda }}_{j,j}:=\lambda _{j,j}(\omega _M) ~ for j\in \{ 1,2\},\nonumber \\ \end{aligned}$$
(16)

the equation of motion of the CFB in an irregular sea of the form as in Eq. (15) can be written as

$$\begin{aligned} \begin{aligned}&(m+c^2{\bar{\mu }}_{1,1}+s^2{\bar{\mu }}_{2,2})\ddot{u}+(c^2{\bar{\lambda }}_{1,1}+s^2{\bar{\lambda }}_{2,2}+s^{{2}}\lambda _{vis ,y}){\dot{u}}\\&\quad +F_d({\dot{u}})+s^2\rho g \pi R^2 u=\\&\sum _{p=1}^{N_comp } Re \lbrace \sqrt{2S(\omega _p)d \omega }(c f_x(\omega _p)+sf_y(\omega _p))e ^{-\mathrm {i}\omega _p t+\mathrm {i}\varepsilon (\omega _p)}\rbrace . \end{aligned} \end{aligned}$$
(17)

Here, \(N_comp \) is the number of harmonic components in the irregular sea with wave frequencies \(\omega _p\). The values of \({\bar{\mu }}_{j,j},\) \({\bar{\lambda }}_{j,j}\), \(f_x(\omega _p)\) and \(f_y(\omega _p)\) are determined for the equilibrium position of the CFB in still water. Thereby, it is assumed that the CFB does not make large amplitude motions and is always in the vicinity of this equilibrium. Therefore, the exact values of the hydrodynamic coefficients, which are continuously dependent on the position of the CFB, are then close to the corresponding values in the equilibrium position.

Table 1 Parameter values of floating system
Full size table
Fig. 2
figure 2

Experimental results for the response of the CFB for water waves of frequency \(\omega =2.57~rad/s \) and for different inclination angles \(\alpha \)

Full size image

2.5 Modeling of power take of system

Harvesting energy from the dynamics of the CFB leads to an additional electrical damping force \(F_{elec }\) in Eq. (8) and Eq. (17). In the following, this damping force is assumed to be linearly dependent on the velocity of the CFB, i.e.

$$\begin{aligned} F_{elec }=\lambda _{elec }{\dot{u}}. \end{aligned}$$
(18)

Here, \(\lambda _{elec }\) is the electrical damping constant. The damping force leads to the mechanical power \(P_mech =F_{elec }{\dot{u}}\), which is related to the electrical power \(P_elec \) by means of the efficiency factor \(\eta _{eff }\) such that \(P_{elec }=\eta _{eff } P_{mech }\). Therefore, the electrical power corresponding to the velocity \({\dot{u}}\) of the CFB is given by

$$\begin{aligned} P_{elec }=\eta _{eff }\lambda _{elec }{\dot{u}}^2. \end{aligned}$$
(19)

In the following, the electrical power will be investigated by simulating the dynamics of the CFB over a prescribed temporal domain and integrating the electrical power \(P_{elec }\) over this time domain to get the corresponding electrical energy.

3 Experimental results

In order to validate the influence of the inclination angle, experimental tests have been executed in the wave flume of the Institute of Mechanics and Ocean Engineering, Hamburg University of Technology. The testing facility has a wave flume of \(12\,m (L) \times 1.5\,m (W) \times 1.5\,m (H) \) with a flap-type wave maker. The dimensions of the floating system, which is shown in Fig. 1, are given in Table 1. The damping coefficients \(d_1\), \(d_2\), \(d_3\) and \(d_lin \), which are used to approximate the influence of mechanical friction, can be determined by means of free decay tests. The corresponding values for an inclination angle of \(\alpha =60^\circ \) can be found in Table 1 as well. The displacement of the CFB has been measured using a linear variable differential transformer (LVDT). The LVDT consists of two statically mounted identical coils and a moving rod with a permanent magnet attached at one end working as a piston inside the coils. The rod’s other end is coupled rigidly to the moving CFB. The position of the magnetic piston inside the coils defines the inductance of each coil. Using an AC excitation current the output voltage of a Wheatstone Bridge changes proportionally to the displacement of the piston and is converted into digital numbers by an A/D converter. The corresponding velocity is obtained by differentiation of the displacement. The resolution of the position measurement is about a tenth of a millimeter.

Figure 2 shows for the wave frequency \(\omega =2.57~rad/s \) the measured temporal behavior of the displacement in direction of the coordinate u. It is depicted that the displacements increase if the inclination angle \(\alpha \) is changed from \(\alpha =90^{\circ }\) to \(\alpha =45^{\circ }\). Since higher displacements are reached in the same time domains, the velocities gets higher as well, from which more electrical work can be harvested.

In order to illustrate the influence of a changing inclination angle for different wave frequencies \(\omega \), RAOs can be computed, which are related to the measured amplitude of the incoming waves and the displacements of the CFB. In Fig. 3 the RAOs of the position and velocity are depicted for different inclination angles and the frequencies \(\omega \in [2,4]\,rad/s \). It is shown that the position as well as the velocity of the CFB grows if the inclination angle \(\alpha \) is changed from \(\alpha =90^{\circ }\) to \(\alpha =60^{\circ }\) and \(\alpha =45^{\circ }\), respectively. From the increased velocity and following Eq. (19), more electrical work can be harvested. It has to be noted that the finite length of the wave flume results into wave reflections. These wave reflections results into the fact that the wave amplitudes of the incoming waves are related to the corresponding wave frequencies. Due to the nonlinear damping, the motion of the CFB does not depend linearly on the amplitude of the water waves. Therefore, experimental results in a wave flume of finite length reflects the displacements of the mechanical system in an open sea only in a limited way. Moreover, it should be noted that a realistic irregular sea mainly contains harmonic wave components in the frequency range \(\omega \in [0.5,1.5]\,\)rad/s. Since the wave flume has only a limited length, only waves with small wavelength fit into the channel. Therefore, we have chosen waves with frequencies in the range of \(\omega \in [2,4]\,\)rad/s in the experiments to show the angular dependency on energy harvesting. In the following, simulations of the mechanical system will be studied in order to get more details about the influence of the inclination angle at the motion of the mechanical system.

Fig. 3
figure 3

Experimentally determined RAOs for the position (a) and velocity (b) of the CFB for different inclination angles \(\alpha \)

Full size image

4 Simulation results

In this section, the simulated dynamical behavior is analyzed based on the equations of motion (8) and (17) of the guided point absorber in regular and irregular waves, respectively. In order to relate the simulation results to the results from the experiment, the geometric and damping parameters from the experiment will be used in the following, as given in Table 1. Moreover, a viscous damping coefficient of \({\lambda _vis,y =13.69\,kg/s }\) has been chosen, whereby the value of \(\lambda _vis,y \) has been taken from the paper of Yeung et al. [20]. It has to be noted that Yeung et al. [20] use a cylinder of different size than described by the parameters of Table 1. In order to study the effect of the inclination angle at the motion of the cylinder, the stated value for \(\lambda _vis,y \) will be used in this study as well.

In Fig. 4 the RAOs of the position and velocity are shown for different inclination angles \(\alpha \) for the case of linear and nonlinear damping. Thereby, Eqs. (13) and (14) are used for the linear case and simulation results of solving Eq. (8) with waves of amplitude \(A=0.1\,m \) are used for the case of nonlinear damping. Corresponding surface plots of these cases using inclination angles \(\alpha \in [10^{\circ },90^{\circ }]\) are shown in Figs. 5 and 6. Comparing Figs. 3 and 4 delivers the same general simulative and experimental dynamical behavior. This means, reducing the inclination angle from \(\alpha =90^ \circ \) to \(\alpha =60^ \circ \) and \(\alpha =45^ \circ \) leads to a growth of the displacement and velocity of the system. Furthermore, an increase of the wave frequency \(\omega \) to a value bigger than \(4\,rad/s \) delivers a decrease of the displacement and velocity of the system. Figures 4, 5 and 6 show that with a decrease of \(\alpha \) the RAOs gets higher maximal values at lower frequencies \(\omega \). This results from the fact that due to the multiplication of the stiffness term \(\rho g \pi R^2\) in Eq. (8) with \(\sin (\alpha )^2\), the eigenfrequency of the mechanical system gets lower for a decrease of \(\alpha \). In both damping cases, the maximal velocity is obtained for \(\omega =2.3\,rad/s \) and \(\alpha =38^ \circ \). Generally, the lowest velocity response is obtained for the vertically inclined case at \(90^{\circ }\).

Fig. 4
figure 4

RAOs of the position (a) and velocity (b) for the case of linear damping and position (c) and velocity (d) for the case of nonlinear damping

Full size image
Fig. 5
figure 5

RAO of the velocity for the case of linear damping from two different perspectives

Full size image
Fig. 6
figure 6

RAO of the velocity for the case of nonlinear damping from two different perspectives

Full size image

Next, the mechanical behavior of the point absorber for the case of an irregular wave excitation is studied. In Fig. 7 the position and velocity of the mechanical system for different wave angles in the presence of an irregular water wave with \(N_comp =100\) harmonic wave components can be seen. The corresponding wave amplitudes are obtained using a Pierson–Moskowitz spectrum with modal frequency \(\omega _M=1\,rad/s \) and significant wave height \(H_s=2\,m \). Nonlinear damping and a water depth of \(10\,m \) are used. It can be seen that for an inclination angle of \(\alpha =90^{\circ }\), the CFB follows the sea surface elevation. However, decreasing the inclination angle \(\alpha \) from \(90^{\circ }\) to \(\alpha =30^{\circ }\), the response amplitude of the CFB gets larger, resulting in higher velocities. Although the simulated velocities reduce if \(\alpha \) is decreased further from \(30^{\circ }\) to \(\alpha =10^{\circ }\), a higher amount of electrical energy can also be harvested in irregular seas if the guided point absorber is inclined compared to the case where the CFB only exerts pure heave motion.

Fig. 7
figure 7

Position (a) and velocity (b) of the point absorber for the case of an irregular wave excitation, nonlinear damping and different inclination angles \(\alpha \)

Full size image
Fig. 8
figure 8

Amount of harvested energy for the case of linear (a) and nonlinear (b) damping

Full size image

5 Simple control strategy for guided point absorber

A known disadvantage of point absorbers is the strong dependency of their energy harvesting performance on the wave frequency of incoming waves. A useful control strategy for adjusting the eigenfrequency of the presented guided point absorber to the frequency of the incoming waves is to adjust the inclination angle of the guided point absorber. This adjustment can be carried out very slowly, since the mean frequency of incoming waves changes slowly in real seas. Typically, a considerable change of sea state can be observed after about 20 min [25].

For adjusting the inclination angle of the guided point absorber, the hydrodynamic forces due to incoming waves can be used to tilt the guidance, which is then locked as soon as the desired inclination angle is reached.

In order to show the effect of fixed or controlled inclination angle \(\alpha \), the corresponding electrical power based on Eq. (19) is investigated using numerical simulations. For this, an electrical damping constant \(\lambda _elec =10\,kg/s \) and an efficiency of \(\eta _eff =0.8\) are used. The dynamic behaviors of the system are each simulated for one hour. Thereby, the parameters given in Table 1 for incident harmonic waves of wave frequencies \(\omega \in \lbrace 0.5,\, 1, \, 1.5, \, 2, \, 2.5, \, 3, \, 3.5, \, 4, \, 4.5, \, 5 \rbrace \,rad/s \) are used. The corresponding electrical power is then integrated with respect to time and summed over all considered wave frequencies. Thereby, the inclination angle \(\alpha \) is fixed or controlled based on the incoming wave frequencies such that the CFB reaches high velocities. The results can be seen in Fig. 8 for linear and nonlinear damping. It can be seen that for the uncontrolled case, an inclination angle of \(\alpha =40^\circ \) leads to the highest energy harvesting outputs.

If the proposed control strategy for the adjustment of the inclination angle \(\alpha \) is used, then the energy harvesting output is further increased. In Fig. 8 it can be seen that the controlled case leads to an increase of energy harvesting output of \(34\%\) in comparison to the best case of fixed inclination angle \(\alpha \). It can also be seen that a too small or too high fixed angle \(\alpha \) results in lower energy outputs. Moreover, in comparison to the case \(\alpha =90^\circ \), which corresponds to the standard case of a vertically moving point absorber, the controlled case leads to an energy increase of \(605\%\). In summary it can be concluded that the proposed adjustment and control of the inclination angle \(\alpha \) exposes an efficient way of increasing the amount of harvested energy.

6 Conclusions

We have investigated a guided point absorber for harvesting ocean wave energy using simulations and experiments. Based on the corresponding results we have found that using a fixed inclined guided point absorber increases the averaged energy harvesting output by a factor of about 4.52 in comparison to a standard vertically heaving point absorber. Since the inclination of the guided point absorber leads to a shift of its eigenfrequency, an optimal response to incident waves can be adjusted. Based on this result, we have proposed a simple control strategy, where the inclination angle is adjusted according to the frequency of incident waves. Using such a control leads to an even higher increase of energy harvesting output by a factor of about 6.05 in comparison to a standard vertical point absorber.