1 Introduction

Synchronization is one of the most common phenomena occurring in oscillating systems in nature and in man-made systems; it inheres to the adjustment of self-sustained oscillators rhythms [1]. Since the beginning of this century, there has been an explosion of studies about synchronization in systems of very different nature such as physical [2,3,4,5,6,7,8,9,10,11,12,13], chemical [14,15,16,17], neuronal [18,19,20,21,22,23,24,25,26], biological [27,28,29,30,31,32,33], and even economic [34]. A paradigmatic example of synchronization is that attained by males of several fireflies species, a phenomenon widely described from qualitative observations [35,36,37], through experiments [38,39,40,41,42,43] or with electronic proxies emulating fireflies [44,45,46,47], and by physico-mathematical models [48,49,50,51,52,53,54] based on differential or difference equations, or on multi-agent interactions. A review about fireflies’ synchronization is given in Ref. [55] and the modeling aspects in Ref. [56], where simple algorithms in the form of rules of a game are introduced. This game, called the “flash game” (FG) [57], is a simple one that drives the players (fireflies) to synchronize. It has been extended for the situation of four different rules and briefly analyzed in Refs. [55, 56].

Here, we perform a complete analysis of the FG for several situations and games with two, three and four players, obtaining for each one of the situations and initial conditions the basins of attraction which give us the information about whether or not the fireflies synchronize and how much time does it take for reaching complete synchronization (all the fireflies flashing together).

The work is structured as follows: in Sect. 2, the configurations and the rules of the game are explained. Section 3 starts with a combination analysis about the possible number of games; additionally, some time series and basins of attraction are shown. The results concerning synchronization time and the situations in which synchronous behavior is attained are exhibited and statistically compared also in Sect. 3 to get an insight about the rules and configuration that favor synchronization. Finally, in Sect. 4, we point out the main conclusions and provide some perspectives of the work.

2 Method: the game and its rules

As stated in Sect. 1, there are several types of models to explain how fireflies synchronize, going from multi-agent systems to continuous or discrete dynamical systems. Here, we address the phenomenon mentioned above with the idea of a simple game early introduced by Stewart and Strogatz [57, 58] for the purpose of explaining fireflies flashing behavior. Actually, the game (FG) consists of a very simple algorithm that in certain cases drives the fireflies to synchronize, emitting their flashes simultaneously.

The FG is a two-dimensional game board played on a polygon of ns sides, each of them containing nb boxes, i.e., \(N = ns \times nb\) boxes on the board. The number of players, or fireflies, is np. The goal of the game is for all fireflies to flash synchronously and simultaneously in the shortest possible time, given a specific set of initial conditions. Despite the easiness of the FG, there have been some recent proposals to exploit the original FG idea to other more realistic situations by means of different rules for the FG [55, 56]. Those rules give the system more flexibility to be adapted to several cases according to the system, and in this way, permitting to capture the main features of entrainment and synchronous behavior in fireflies. We formulate the proposed rules for the FG as:

  1. 1.

    The first box plays the role of the flashing box, i.e., when a player (firefly) arrives at this box, it flashes.

  2. 2.

    Each firefly starts the game in any box (initial condition) except the flashing one.

  3. 3.

    Each firefly advances clockwise one position per time step, except when other(s) firefly(ies) attain(s) the flashing box, changing the dynamics according to Rule 4.

  4. 4.

    When a firefly reaches the flashing box, it remains in that position for one time-step. On the other hand, the other fireflies go forward according to the number of the side of the polygon (ns) on which they are located: when a firefly is on a box of the first side, it advances one position as in Rule 3, when it is on a box of the second side, it moves forward two positions, and thus when it is on a box of the nth side, it runs ahead n positions.

  5. 5.

    Repeat from Rule 3 to update the position of the players.

The rules mentioned above might allow or not the occurrence of complete synchronization. The game’s dynamics strongly depend on the initial conditions and Rule 4 because it determines what happens to a firefly when it approaches, arrives, or passes through the flashing box. We consider the following four complementary variants of Rule 4, named nr:

  1. (a)

    When a firefly is in a box located on the last side of the polygon, it might overtake the flashing box without flashing in its cycle. This fact imposes a difficulty in attaining complete synchronization. This variant represents the basic Rule 4, as it does not impose any constraints.

  2. (b)

    No firefly can overtake the flashing box, even if it has received an impulse that would push it to pass over the flashing box. Instead, it has to stop at the flashing box, and the remaining fireflies update their cycle positions accordingly (unless they are already at the flashing box). This means that fireflies cannot complete a cycle without flashing.

  3. (c)

    When a firefly reaches the flashing box, the others advance as stated in Rule 4 due to the excitatory coupling. It is possible that during this flashing, one or more other fireflies also reach the flashing box, resulting in more than one firefly on that box. Due to inhibitory coupling, these fireflies continue to flash and wait until no more fireflies reach that position. When two or more fireflies are in the flashing box, the other fireflies advance only one position instead of the n positions specified in the Rule 4.

  4. (d)

    Finally, considering a similar situation as in (c) but with the modification that when the fireflies are forced to stay in the flashing box, the other fireflies advance according to the standard Rule 4 and not only one position.

The rules mentioned above are the basis of the work for an in-depth analysis of the FG. Note that for two players, the variants (c) and (d) of Rule 4 lead to the same results than variant (b).

To illustrate how the game works, we represent in Fig. 1a some frames of the game evolution reflecting the rules (a)–(d) when \(np=4\) with the initial conditions \((p_{01},p_{02},p_{03},p_{04})=(5,9,14,18)\), and some other possibilities for the cardboard as the triangular and octagonal shapes shown in Fig. 1b, c.

Fig. 1
figure 1

a Frames of the game evolution for four players (fireflies) and the rules (a)–(d) considering for all the four cases the same initial conditions \((p_{01},p_{02},p_{03},p_{04})=(5,9,14,18)\). Some other possibilities for the cardboard: b triangle and c octagon

Full size image

3 Results and discussion

As it is expected, the number of possibilities (results) for the game is quite large and depends strongly on np, ns and nb. A simple combinatorial permits us to compute all the possible games ng by means of the following expression:

$$\begin{aligned} ng=nr\sum _{i=np_{\mathrm {low}}}^{np_{\mathrm {high}}}\sum _{j=ns_{\mathrm {low}}}^{ns_{\mathrm {high}}}\sum _{k=nb_{\mathrm {low}}}^{nb_{\mathrm {high}}}(j\times k-1)^i, \end{aligned}$$
(1)

where \(np_{\mathrm {low}}\), \(np_{\mathrm {high}}\), \(ns_{\mathrm {low}}\), \(ns_{\mathrm {high}}\), \(nb_{\mathrm {low}}\) and \(nb_{\mathrm {high}}\), being respectively the lower and higher considered values for the number of players, sides and boxes per side. In particular, the lower number of the quantities refers to the minimum number of these quantities that makes sense to the game. For instance, we need at least two players, the number of sides to complete a circuit is a minimum of three, and the number of boxes per side must be at least two. Concerning the computation of the number of games ng using Eq. 1, we first consider the simplest case when the quantities are fixed: \(np=2\), \(ns=3\), \(nb=2\), and also the number of rules \(nr=4\), we have:

$$\begin{aligned} ng=nr\times (ns\times nb - 1)^{np}=4\times (3\times 2-1)^2 = 100 . \end{aligned}$$

In this work, we choose the following values: \(nr=4\), \(np_{\mathrm {low}}=2\), \(np_{\mathrm {high}}=4\), \(ns_{\mathrm {low}}=3\) (triangle), \(ns_{\mathrm {high}}=9\) (nonagon), \(nb_{\mathrm {low}}=2\) and \(nb_{\mathrm {high}}=9\). With these values, Eq. (1) gives the total number of possible games \(ng=891585408\) a quantity that approaches \(9\times 10^8\). To have a more detailed insight about these possibilities, we show the breakdown of each of the situations depending on the number of sides and boxes.

Table 1 Number of possible games when the number of players is \(np=2\) and for the four variants (\(nr=4\)) according to the number of sides of the polygon ns and the number of boxes per side nb
Full size table
Table 2 Number of possible games when the number of players is \(np=3\) and for the four variants (\(nr=4\)) according to the number of sides of the polygon ns and the number of boxes per side nb
Full size table
Table 3 Number of possible games when the number of players is \(np=4\) and for the four variants (\(nr=4\)) according to the number of sides of the polygon ns and the number of boxes per side nb
Full size table
Fig. 2
figure 2

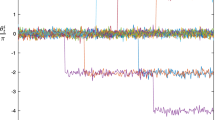
First row: a, b time series for the evolution of two fireflies following the rules (a) and (b) above mentioned when the cardboard is a rectangle (\(ns=4\)) with \(nb=9\); c, d for the evolution of two fireflies following the rules (a) and (b) when the cardboard is a nonagon (\(ns=9\)) with \(nb=4\). The initial conditions in all cases are \((p_{01},p_{02})=(2,22)\). Fireflies 1 and 2 evolution are represented with black and orange lines, respectively. Second row: e, f basins of attraction for two fireflies and considering the rules (a) and (b) when the in a, b; g, h when the cardboard is that used in c, d. White boxes represent situations in which simultaneous, collective, and persistent flashing (in every cycle) are not achieved, i.e., there is no complete synchronization

Full size image
Fig. 3
figure 3

Two-dimensional sections of the basins of attraction for rules (a)–(d) for four players (fireflies) with a set of initial conditions \((p_{01},p_{02})=(37,37)\), (first row) when playing with an octagon shape board (\(ns=8\)), with nine boxes per side (\(nb=9\)); (second row) f–i when playing with a nonagon shape board (\(ns=9\)), with eight boxes per side (\(nb=8\)). e, j Box plots (median and quartiles) of the synchronization times related to the basins a–d and f–i. The percentage of the synchronous events is shown in the upper part, above the whisker

Full size image

To analyze the numerous possibilities of the game, we first inspected all the time series determining the synchronization time. Second, we obtained the basins of attraction of each possible game, determining the median synchronization time, first and third quartiles, and the percentage of synchronized events. Finally, based on the information from Tables 1, 2 and 3, we performed statistical tests to compare the features of the results according to the geometry and number of boxes of the cardboard, the number of players, and the used rule.

To have a glimpse of those steps, in Fig. 2, we chose possible games when \(np=2\) and the cardboards have the same number of boxes (\(nb=36\)), but with different geometries in them; for the first cardboard, the geometry is a rectangle (\(ns=4\)) with nine boxes per side (\(nb=9\)), and for the second, the shape is a nonagon (\(ns=9\)) with four boxes per side (\(nb=4\)). As mentioned above, when the number of players is two, only the rules (a) and (b) are relevant because rules (c) and (d) reduce to rule (b) in this case. The time series corresponding to rules (a) and (b) for the rectangular cardboard are shown in Fig. 2a, b respectively, and in the same order for nonagonal cardboard in Fig. 2c, d. In all cases, the set of initial conditions are: \((p_{01},p_{02})=(2,22)\). Nevertheless, for the rectangular cardboard and rule (a), it is essential to remark that considering the formal definition of synchronization, the phase difference among the fireflies remains constant from around the 100th turn, which constitutes phase-synchronization. Still, fireflies 1 and 2 do not flash in every cycle, and consequently, they do not flash simultaneously. On the contrary, when the rule is (b), the synchronization time is 423 time steps. In the case of a nonagon, the synchronization time for rules (a) and (b) are 400 and 262 turns (time steps), respectively. The basins of attraction are represented in Fig. 2e, f following the same order of the first row. A simple inspection of the basins of attraction shows that for the rectangular shape under the rule (a), the complete synchronization is rare (Fig. 2e). On the contrary, when rule (a) is considered for the nonagonal shape, complete synchronization is always achieved (Fig. 2g). When the rule is (b), the basins of attraction for the rectangular and nonagonal cardboard look similar (Fig. 2f, h). Even though, for the rectangular case, two diagonals of the basin of attraction show initial conditions that do not lead to complete synchronization. In contrast, for the nonagon, all the initial conditions lead to complete synchronization. It is interesting to note that rule (c) has the largest proportion of initial conditions leading to complete synchronization, but the largest synchronization times—see Fig. 3e. We remark that the computation of the basins of attraction is related to the elapsed time (turns) to achieve complete synchronization with simultaneous collective flashing.

We obtain some other 2-D sections of the basins of attraction for four fireflies. Indeed, we now consider two boards of boxes, one in octagon (\(ns=8\)) and another in nonagon (\(ns=9\)) form, with nine (\(nb=9\)) and eight (\(nb=8\)) boxes per side respectively, and initial conditions \((p_{01},p_{02})=(37,37)\). The basins of attraction for each rule are shown in Fig. 3a–d when the board is an octagon, and in Fig. 3f–i when the board is a nonagon. Note that in each panel, there is an upper color bar showing in its extremes the situation of “no sync”, and the maximum synchronization time. The corresponding box plots displaying the medians and the quartiles related to synchronization time as well as the percentage of complete synchronization events for each rule are shown in Fig. 3e, j for the case of the octagon and nonagon, respectively.

A visual and qualitative insight of the results set out that, as expected, rule (a) is the less favorable to attain complete synchronization. On the other hand, for the octagon, the results of rules (b) and (d) seem to be very similar, but the rule (d) is slightly more favorable to complete synchronization. Similarly, the visual inspection for the nonagon shows us that for rule (c), in almost all cases, complete synchronization is achieved (99.25%), but in contrast, the synchronization times are considerably longer than for rules (b) and (d). We also note that rule (a) for the nonagon does not permit complete synchronization; the only situation considered as synchronization is that all the initial conditions are the same. We also perceive that rules (b) and (d) are pretty similar in the case of the octagon. Finally, comparing the basins of attraction of octagon and nonagon, we found that they remarkably resemble for all the rules.

The statistical analysis for the octagon (\(ns=8\), \(nb=9\) and \(np=4\)) indicates that the median time of synchronization is the longest for the rule (c) and the shortest for the rule (d). As the times of synchronization do not follow a normal distribution, a Kruskal–Wallis test was performed to look for differences in the distribution of the four rules (\(\chi ^2=1290.5\), \(df=3\), \(p<2.2\times 10^{-16}\)). A Dunn’s test for multiple comparisons showed that all pairwise comparisons between rules (a) to (d) are significantly different (\(p<0.05\)), except between rules (a) and (b) (\(p=0.84\)). The percentages of initial conditions for rules (a) to (d) leading to complete synchronization were respectively 3.19%, 96.03%, 99.96%, and 96.63%. Thus, we can conclude that when using rule (d), the number of initial conditions leading to complete synchronization is very high with the shortest times.

For the case of the nonagon (\(ns=9\), \(nb=8\) and \(np=4\)), the median time is the longest for rule (c) and the shortest for rule (d) (defining \(t_s\) as the synchronization time for achieving complete synchronization, \(t_{s}\)(c) > \(t_{s}\)(b) > \(t_{s}\)(d)). Note that the median time for rule (a) (\(t_{s}\)(a)) is only computable when all initial conditions are the same. As the Kruskal–Wallis test was significant (\(\chi ^2=1788.3\), \(df=3\), \(p<2.2\times 10^{-16}\)), a Dunn’s test of multiple comparisons was performed. All the pairwise comparisons were highly significant (\(p<0.001\)) except the comparisons with the rule (a), because the basin of attraction with rule (a) does not show any initial condition leading to synchronization, unless all the initial conditions are the same. The percentages of initial conditions for rules (a) to (d) leading to complete synchronization were, respectively, 0.02% (when all the initial conditions are the same), 95.20%, 99.25% and 94.72%.

Fig. 4
figure 4

Summary of the statistical analysis of the FG showing the median of the synchronization time according to the number of sides ns, of boxes per side nb and for each number of players np. The color bar is related to the percentage of totally synchronized events

Full size image

After the analysis of the examples mentioned above, we perform a complete analysis for all the possible basins of attraction based on the median of synchronization time and the percentage of complete synchronized events as it is illustrated in Fig. 4. We explored all the cases concerning the initial conditions for the statistical analysis, i.e., each game related to a set of initial conditions and, consequently, to a synchronization time. In other words, with this we are able to reconstruct the 3-D or 4-D basins of attraction. The results exhibited in Fig. 4 indicate that, in general, rule (d) leads to better synchronization, i.e., with the shortest median of synchronization time and the highest percentage of synchronized events. Undoubtedly, rule (a) is the less favorable to synchronization with a low percentage of total synchronized events.

A last remark to highlight consists of the tendency to achieve almost 100% of synchronized events when the number of sides of the cardboard increases and consequently the number of total boxes. This last aspect might be related to the assertion that the bigger the board, the richer the dynamics the dynamics of the game.

Finally, we carry out a comparison among groups of games having the same total number of boxes. Concretely, we analyzed 27, 32, and 72 boxes for the studied cases of two, three and four players, and considering the possible rules for each case, namely rules (a) and (b) for two players, and rules (a), (b), (c) and (d) for three and four players. The details of the comparison are shown in Table 4 in the two last main columns showing the differences between groups considering the shortest median synchronization time including the first and third quartiles, and the highest percentage of synchronized events (this remark is made due to the fact that each group might contain several basins of attraction).

The results exhibited in these two main columns are the p value which indicates whether the groups belong or not to the same distribution, and the above-mentioned results of synchronization time and the percentage of synchronized events for each group denoted by b followed by np, ns, nb. Thus, for instance when the total number of boxes is 27, the group b239 indicates two players, three sides (triangle) and nine boxes per side while b493 stands for four players, nine sides (nonagon) and three boxes per side. The comparison analysis has been performed considering all the two-dimensional sections of the basin of attraction corresponding to the features of the group, e.g., for two players each group consists of one 2-D basin of attraction; for three players, the group b348 contains 31 2-D sections of the basin of attraction; and for four players, the group b498 involves 5041 2-D sections of the basin of attraction. The main results obtained for this comparative analysis are summarized as follows:

  • All the statistical tests are significant (\(p\le 0.01\)).

  • For 27 boxes, we observe that the synchronization time is shorter when the board is a nonagon, except for the rule (a). In what respect the percentage of synchronized events, the nonagon configuration leads to greater values.

  • For 32 boxes, as regards to the synchronization time, there is a similar behavior than in the case of 27 boxes, i.e., the board with more sides (octagon) exhibits shorter values than the rectangle, except for the rule (a). On the contrary, the percentage of synchronized events is greater for the rectangular configuration, except for the rule (a).

  • For 72 boxes, the synchronization time is always shorter for the nonagonal structure while the percentage of synchronized events are greater for the octagon board.

Table 4 Statistical analyses of the cases with 27, 32, and 72 boxes in total
Full size table

4 Conclusions and perspectives

With its four basic rules (algorithms), this simple game allows us to explain the occurrence of complete synchronization in some fireflies species. Moreover, it has an intrinsic dynamical richness since these simple rules might be translated to a more technical language belonging to synchronization theory. Thus, it is possible to find a relation between the number of sides and boxes per side with the type of coupling. According to the considered rules, the game evolves as a system of pulse-coupled oscillators, occurring an excitatory or inhibitory coupling when one or more players attain the flashing box. The flashing of one or more fireflies pushes the others to reach the flashing box (excitation). On the contrary, the flashing fireflies retain themselves in this position for a certain number of turns (inhibition). We performed intensive numerical work obtaining the time series to determine synchronization. We also computed the basins of attraction to identify the specific features of all possible games. The differences between the rules show that the primary rule (a) is not the most adequate for attaining synchronization. Then, we complete our statistical analysis establishing as a criterion for comparing the groups the considered rule. In general, we find that the distributions related to each group are different compared to the other groups. Nevertheless, it is important to emphasize that rule (a) has peculiar features which do not necessarily lead to complete synchronization. Our results also demonstrate that as more sides have the polygons, the better the synchronization is achieved, i.e., both in what concerns the synchronization time and the percentage of synchronization. Although the game and its possibilities have been widely explored, several aspects could be studied in future works. Thus, it is possible to formulate rules that incorporate inhibitory coupling or rules combining excitatory and inhibitory coupling as it happens in several fireflies species. Another aspect of being analyzed is the possibility of including “silence times” as it occurs in some fireflies species. A final consideration might include players following different rules associated with the diverse dynamics attributed to fireflies, males and females.