Finite-size effects, demographic noise, and ecosystem dynamics

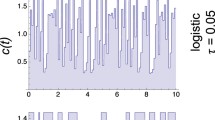
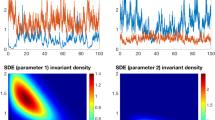
Abstract

Strong positive feedback is considered a necessary condition to observe abrupt shifts in ecosystems. A few previous studies have shown that demographic noise—arising from the probabilistic and discrete nature of birth and death processes in finite systems—makes the transitions gradual. In this paper, we investigate the impact of demographic noise on finite ecological systems. We use a simple cellular automaton model with births and deaths influenced by positive feedback processes. We present our methods in a tutorial like format. Using the approach of van Kampen’s system-size expansion, we derive a stochastic differential equation that describes how local probabilistic rules scale to stochastic population dynamics in finite systems. We illustrate that as a consequence of enhanced demographic noise, finite-sized ecological systems can show an ‘effective abrupt transition’ even with weak positive interactions. Numerical simulations of our spatially explicit model confirm this analytical expectation. Thus, we predict that small-sized populations and ecosystems, in response to environmental drivers, are prone to abrupt collapse while larger systems—with the same microscopic interactions—show a smooth response.

Appendices

Appendix A: Mean-field approximation

To write the mean-field equation for the dynamics of the model, we assume infinite size and no spatial structure in the ecosystem, meaning each site in the system is equally likely to be occupied. The probability of any site being occupied is same as the global occupancy. Therefore, the transition rates in this model are as follows. Transition rate for a site to change from 1 to 0 :

$$\begin{aligned} \omega (1 \rightarrow 0) = d (1-\rho ) + (1-q){\text {d}}\rho \end{aligned}$$

(Here d is the death rate, not the symbol for a differential). Similarly, transition rate from 0 to 1:

$$\begin{aligned} \omega (0 \rightarrow 1) = p \rho + q\rho ^2. \end{aligned}$$

Probability of finding a site in occupied(1) state : $P(1)=\rho$ and probability of finding a site in state in empty(0) site: $P(0)=(1-\rho )$

The master equation can then be written as:

$$\begin{aligned} \frac{{\text {d}}P(1)}{{\text {d}}t} = \omega (0 \rightarrow 1)P(0) - \omega (1 \rightarrow 0) P(1). \end{aligned}$$

Substituting the above transition rates,

$$\begin{aligned} \frac{{\text {d}}\rho }{{\text {d}}t}= f(\rho ) = (p-d)\rho - (p-q-qd)\rho ^2 - q\rho ^3. \end{aligned}$$

(14)

For simplicity, the above equation can be written in terms of a, b and c as:

$$\begin{aligned} f(\rho ) = a\rho - b\rho ^2 - c\rho ^3, \end{aligned}$$

(15)

where $a=p-d$, $b=p-q-qd$ and $c=q$. At equilibrium, $\frac{{\text {d}}\rho }{{\text {d}}t}=0$. This gives the following equilibria:

$$\begin{aligned} \rho \text {*}=0 , \rho \text {*} = -\frac{b}{2c}+\root \of {\frac{b^2}{4c^2} + \frac{a}{c}}\text { and } \rho \text {*} = -\frac{b}{2c}-\root \of {\frac{b^2}{4c^2} + \frac{a}{c}}. \end{aligned}$$

We call these solutions as $\rho _0$ , $\rho _A$ and $\rho _B$ respectively. For the above equilibria to be stable, $f'(\rho \text {*})<0$.

From (15), we get:

$$\begin{aligned} f'(\rho )= & {} a\rho - b \rho ^{2} -c \rho ^{3}\nonumber \\ f'(\rho )|_{\rho _0}= & {} a \nonumber \\ f'(\rho )|_{\rho _A}= & {} -2a - \frac{b^2}{2c} + b \root \of {\frac{a}{c}+ \frac{b^2}{4c^2}} \nonumber \\ f'(\rho )|_{\rho _B}= & {} -2a - \frac{b^2}{2c} - b \root \of {\frac{a}{c}+ \frac{b^2}{4c^2}}. \end{aligned}$$

(16)

In this analyses, we consider $c>0$ because $c=q$ in our model which is a probability. From the above three equilibrium densities, only real and positive solutions are realistic. Therefore, we will reject the negative solutions. For the non-zero solutions to be real, $a>-\frac{b^2}{4c}$

1.1 Case 1: $b>0$

In this parameter region, given $a>-\frac{b^2}{4c}$, $\rho _B$ is always negative. Therefore, the mean-field equation has only two solutions $\rho _0$, which is stable for $a<0$ and $\rho _A$, which is stable for $a>0$. At $a=0$, $\rho _A = 0$ and it increases monotonically after that. The mean-field system undergoes a continuous transition (also called second-order transition or trans-critical bifurcation) at a critical point $a=0$ for all values of $b>0$.

1.2 Case 2: $b<0$

In this parameter regime, $\rho _0$ is stable for $a<0$ and unstable for $a>0$. $\rho _B$ is real and positive only when $\frac{-b^2}{4c}< a < 0$ and it is unstable in this regime. $\rho _A$ is stable for $a \ge \frac{-b^2}{4c}$. At $a = \frac{-b^2}{4c}$, $\rho _A = \frac{|b|}{2c}$. The mean-field system shows a saddle-node bifurcation at the point $(a,\rho ^*) = (\frac{-b^2}{4c}, \frac{|b|}{2c})$. The transition from an active phase (vegetated state) to absorbing phase (bare state) is discontinuous.

In the mean-field approximation, our model undergoes a continuous transition when $b>0$ and a discontinuous transition when $b<0$. The system has a tri-critical point at $a=0, b=0$ where the nature of transition changes from continuous to discontinuous. Now, translating it back to our system (Eq. 14) with parameters p, q and d,the tri-critical point occurs at $p_t=d$ and $q_t=\frac{d}{1+d}$. For $q<q_t$, continuous phase transition occurs at $p_c=d$. However, the critical point ($p_{c_1}$) decreases as a function of q when $q>q_t$. Therefore, in discontinuous regime, the vegetated state can sustain harsher conditions represented by low values of p when strength of positive feedback among plants is high. However, when the external conditions pass a threshold, the system collapses abruptly to the bare state.

Appendix B: Pair approximation

In the mean-field approximation, we assumed that each site on the lattice has equal probability of being occupied by a plant and that there are no spatial fluctuations in the system. We now incorporate the local spatial effects in the master equation. We assume that the probability of occupancy of a site depends on the state of its nearest neighbours. Therefore, we introduce conditional probability $q_{i|j}$ defined as probability that a site is in state i given its nearest neighbour is in state j. In this approximation we have singlet density $\rho _1$ (same as mean-field approximation) and an additional doublet density ($\rho _{ij}$) defined as the probability of a site being in state i and its neighbour being in state j. The pair ij has the following properties in this approximation.

$$\begin{aligned} \rho _{ij} = \rho _{ji} \quad \rho _{ij} = \rho _i~q_{j|i} \quad q_{j|i} = 1- q_{i|i}. \end{aligned}$$

(17)

Note that i and j can be 0 or 1. For singlet density ($\rho _1$), the master equation can be written as:

$$\begin{aligned} \frac{{\text {d}}\rho _1}{{\text {d}}t} = \omega (0 \rightarrow 1)\rho _0 - \omega (1 \rightarrow 0) \rho _1. \end{aligned}$$

(18)

The transition rates $\omega (0 \rightarrow 1)$ and $\omega (1 \rightarrow 0)$ are defined as follows:

$$\begin{aligned}&\omega (0 \rightarrow 1)= p~q_{1|0} + q~q_{1|0}~q_{1|1} \nonumber \\&\quad \text {and} \quad \quad \omega (1 \rightarrow 0) = d~q_{0|1} - (1-q)~d~q_{1|1}. \end{aligned}$$

(19)

Here p is the baseline birth probability, q is the positive feedback parameter and d is the death probability. Substituting Eq. (19) in Eq. (18) and using the fact that $\rho _{ij} = \rho _{ji}$ and $\rho _{ij} = \rho _i~q_{j|i}$ (Eq. 17) we obtain the following form for the master equation

$$\begin{aligned} \frac{{\text {d}}\rho _1}{{\text {d}}t} = \left\{ p~q_{0|1} + q~q_{1|1}~q_{0|1} - d~q_{0|1} - (1-q)~d~q_{1|1} \right\} \rho _1.\nonumber \\ \end{aligned}$$

(20)

Similarly, for the doublet density ($\rho _{11}$), the master equation can be written as

$$\begin{aligned} \frac{{\text {d}}\rho _{11}}{{\text {d}}t}= & {} \omega (10 \rightarrow 11)\rho _{10} + \omega (01 \rightarrow 11)\rho _{01} \nonumber \\&- \omega (11 \rightarrow 01)\rho _{11} - \omega (11 \rightarrow 10)\rho _{11}\nonumber \\= & {} 2 \lbrace \omega (10 \rightarrow 11)\rho _{10}\rbrace - 2 \lbrace \omega (11 \rightarrow 10)\rho _{11}\rbrace . \end{aligned}$$

(21)

The transition rate $\omega (10 \rightarrow 11)$ is defined as

$$\begin{aligned} \omega (10 \rightarrow 11)= & {} \frac{1}{z}~p + \frac{z-1}{z}~p~q_{1|0}\nonumber \\&+ \frac{1}{z}~q~q_{1|1} + \frac{z-1}{z}~q~q_{1|0}~q_{1|1}. \end{aligned}$$

(22)

Here z is the number of nearest neighbours. The first term represents the rate of the event in which the 1 in the pair 10 reproduces at 0 with probability p. The second term represents the rate of the event in which a neighbour of 0 in the pair 10 other than the 1 in the pair is also 1 (we call such neighbours as non-pair neighbours; this occurs with probability $q_{1|0}$) and it reproduces at 0 with probability p. The next two terms represent the growth rate due to positive feedback. The third term represents the event in which a non-pair neighbour of the 1 in 10 is also occupied (this occurs with probability $q_{1|1}$) and a birth occurs with enhanced probability q at 0 of the pair. The last term represents the event in which a non-pair neighbour of the 0 in 10 is occupied (this occurs with probability $q_{1|0}$) and its next neighbour is also occupied (this occurs with probability $q_{1|1}$) and a birth occurs at the 0 of the pair with enhanced probability q.

Similarly, we define the transition rate $\omega (11 \rightarrow 10)$ as

$$\begin{aligned} \omega (11 \rightarrow 10)= & {} \frac{1}{z}(1-q)~d \nonumber \\&+ \frac{z-1}{z}(1-q)~d~q_{1|1} + \frac{z-1}{z}d~q_{0|1}.\qquad \end{aligned}$$

(23)

The first term represents the rate of the event in which a 1 in the pair 11 dies with a diminished probability $(1-q)d$ due to the facilitative interaction with the other 1 of the pair. The second term represents the rate of the event in which a non-pair neighbour of 1 in the pair 11 (which we call focal to distinguish it from the other 1 of the pair) is occupied (this occurs with probability $q_{1|1}$) and the focal 1 dies with a diminished probability $(1-q)d$ due to the facilitative interaction with this non-pair neighbour. The third term represents the rate of the event in which a non-pair neighbour of the focal 1, is 0 (this occurs with probability $q_{0|1}$) and the focal 1 dies with probability d.

Fig. 5

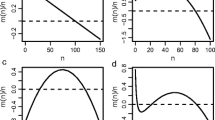
Bifurcation diagram obtained by pair approximation analysis. A and B show the continuous and discontinuous transitions at $q<q_t$ and $q>q_t$ respectively. C is the full phase diagram as a function of q and p.The black dot represents the tri-critical point $q=q_t$ at which the nature of transition changes from continuous to discontinuous. The region between solid and dotted black lines is the bistable region

Substituting Eqs. (22) and (23) in Eq. (21), the master equation for the doublet density takes the following form

$$\begin{aligned} \frac{{\text {d}}\rho _{11}}{{\text {d}}t}= & {} 2 \left\{ \lbrace \frac{1}{z} p +\frac{z-1}{z} p~q_{1|0} \right. \nonumber \\&\left. + \frac{1}{z} q~q_{1|1} + \frac{z-1}{z} q~q_{1|0}~q_{1|1} \rbrace \rho _{10} \right\} \nonumber \\&-2\left\{ \lbrace \frac{1}{z}(1-q)~d + \frac{z-1}{z}(1-q)~d~q_{1|1} \right. \nonumber \\&\left. + \frac{z-1}{z}d~q_{0|1}\rbrace \rho _{11} \right\} . \end{aligned}$$

(24)

We are interested in two dimensional landscapes modelled by a square lattice. We use a von-Newmann neighbourhood $(z=4)$ in all our analyses. Note that using the properties in Eq. (17), we may write $\rho _{10}=(q_{0|1}/q_{1|1})\rho _{11}.$ Further, we may write $q_{1|1}=1-q_{0|1}.$ Substituting these in Eqs. (20) and (24) we obtain

$$\begin{aligned} \frac{{\text {d}}\rho _1}{{\text {d}}t}= & {} M_1 \rho _1 \\ \frac{{\text {d}}\rho _{11}}{{\text {d}}t}= & {} M_{11} \rho _{11} \end{aligned}$$

$M_{1}$ and $M_{11}$ are defined as follows

$$\begin{aligned} M_1= & {} p~q_{0|1} + q~(1-q_{0|1})~q_{0|1} \nonumber \\&- d~q_{0|1} - (1-q)d~(1-q_{0|1}) \end{aligned}$$

(25)

$$\begin{aligned} M_{11}= & {} 2 \left( ~\frac{1}{4}~p~\frac{q_{0|1}}{(1-q_{0|1})} + \frac{3}{4} p~q_{1|0}~\frac{q_{0|1}}{(1-q_{0|1})}\right. \nonumber \\&\left. + \frac{1}{4} q~q_{0|1} +\frac{3}{4} q~q_{1|0}~q_{0|1} \right) \nonumber \\&- 2 \left( ~\frac{1}{4}(1-q)~d + \frac{3}{4} (1-q)~d~(1-q_{0|1})\right. \nonumber \\&\left. + \frac{3}{4} q_{0|1}~d ~\right) \end{aligned}$$

(26)

$\rho _1 = 0$ and $\rho _{11}=0$ give the trivial equilibria. In addition, $M_1 = 0$ and $M_{11}= 0$ provide other equilibria of the system. To ease the notation, we substitute $q_{0|1}=\mathbf{a}$ in Eq. (25), set $M_{1}=0$ and simplify to obtain a quadratic equation in $\mathbf{a}$

$$\begin{aligned} q \mathbf{a^2} - \left[ p + q(1-d) \right] \mathbf{a} + d(1-q) = 0. \end{aligned}$$

(27)

Assuming $q \ne 0$, the two solutions $\mathbf{a_+}$ and $\mathbf{a_-}$ are:

$$\begin{aligned} \mathbf{a_+}= & {} \frac{p + q(1-d) + \sqrt{ \left[ p+q(1-d)\right] ^2 - 4q(1-q)d }}{2q},\qquad \end{aligned}$$

(28)

$$\begin{aligned} \mathbf{a_-}= & {} \frac{p + q(1-d) - \sqrt{ \left[ p+q(1-d)\right] ^2 - 4q(1-q)d }}{2q}.\qquad \end{aligned}$$

(29)

Now, we substitute $q_{0|1}=\mathbf{a}$ and $q_{1|0} = \mathbf{b}$ in Eq. (26), set $M_{11}=0$ and simplify to obtain a solution for $\mathbf{b}$ assuming $3 {\mathbf {a}} [p + q(1- {\mathbf {a}})] \ne 0$

$$\begin{aligned} {\mathbf {b}} = \frac{ (1-{\mathbf {a}})\lbrace {(1-q)d\left[ 1+3(1-{\mathbf {a}})\right] + {\mathbf {a}}\left( 3d-q\right) \rbrace } - p{\mathbf {a}}}{3 {\mathbf {a}} [p + q(1- {\mathbf {a}})]}.\nonumber \\ \end{aligned}$$

(30)

Density ($\rho _1$) can be calculated from $q_{0|1}$ and $q_{1|0}$ as following

$$\begin{aligned} \rho _1= & {} \frac{\rho _{10}}{q_{0|1}} = \frac{\rho _{01}}{q_{0|1}} = \frac{\rho _0~q_{1|0}}{q_{0|1}} \nonumber \\ \rho _1~q_{0|1}= & {} (1-\rho _1)~q_{1|0} \nonumber \\ \rho _1= & {} \frac{q_{1|0}}{q_{0|1}+q_{1|0}} = \frac{\mathbf{b}}{\mathbf{a}+\mathbf {b}}. \end{aligned}$$

(31)

Therefore, the steady-state density can be calculated from Eq. (31) where a and b can be obtained from Eqs. (28), (29) and (30).

1.1 Case 1: No positive feedback ($q=0$)

The master equation for the singlet and doublet density reduces to the contact process when $q=0$ [64]. We know that the contact process model undergoes a continuous phase transition [65], where density of active cells (vegetation density in our case) decreases to zero continuously. Therefore, at the critical point ($p_c$), the density ($\rho _1$) goes to zero. Substituting $q=0$ and $p=p_{{\text {c}}}$ in Eq. (27)

$$\begin{aligned} -p_{\text {c}} \mathbf{a} + d = 0 \implies \mathbf{a} = \frac{d}{p_{\text {c}}}. \end{aligned}$$

Because $\rho _1 = 0$ at $p=p_{{\text {c}}}$, Eq. (31) implies $\mathbf{b} = 0.$ Substituting $q=0$, $p=p_{{\text {c}}}$, ${\mathbf {a}}=d/p_{{\text {c}}}$ and ${\mathbf {b}}=0$ in Eq. (30), assuming $d \ne 0$ and simplifying we get

$$\begin{aligned} p_{{\text {c}}} = \frac{4}{3}d. \end{aligned}$$

(32)

Thus, given that the contact process exhibits a continuous phase transition, the pair approximation predicts a critical point $p_{\text {c}}=\frac{4d}{3}.$ This result is consistent with the results of [64].

1.2 Case 2: With positive feedback ($q>0$)

Now, we investigate the role of positive feedback on phase transition in our model. For $q>0$, ${\mathbf {a}}$ will have two solutions given by Eqs. (28) and (29). Therefore, substituting these in Eq. (30) to obtain ${\mathbf {b}}$ and then substituting ${\mathbf {a}}$ and ${\mathbf {b}}$ in Eq. (31), vegetation density will have two non-zero values for some values of p and d. From mean-field approximation, we know that one of these solutions is stable and the other is unstable. The region in parameter space where these two solutions (one stable and one unstable) coexist and are positive will show the discontinuous transition. Indeed for a fixed $d=0.3$, the system shows continuous transition for low values of q and discontinuous transition for high values of q.

We define the critical point $p=p_{{\text {c}}}$ as the point where vegetation density drops to zero. At the critical point for discontinuous transition, two non-zero solutions of $\rho _1$ (one stable and one unstable) meet. This occurs where determinant in Eq. (28) or Eq. (29) vanishes.

$$\begin{aligned} \left[ p_{\text {c}} +q(1-d)\right] ^2 - 4q(1-q)d = 0. \end{aligned}$$

Since $p_c, q$ and d are non-negative, we have

$$\begin{aligned} p_c = \sqrt{4q(1-q)d} - (1-d)q. \end{aligned}$$

At the tri-critical point ($q=q_t$), the transition changes from continuous to discontinuous (see 5). Therefore, at this point, the critical density (defined as the density at which transition occurs) is zero. Substituting these values in Eq. (30) for $d=0.3$, we get, $(p_t,q_t)=(0.27,0.36)$.

In the continuous transition regime ($q<q_t$), unlike the mean-field approximation, critical point decreases as a function of q. This shows that in our model, positive feedback in the systems with local spatial interactions helps the system sustain its vegetated state in harsh conditions which are represented as low values of p. Note that we did not perform stability analysis for this model. However, it is reasonable to assume that the stability of the equilibria will remain the same as the mean-field model. The bifurcation diagram obtained by the pair approximation is shown in Fig. 5. It is qualitatively same as the output of mean-field model. However, it is clear that the vegetated state is sustained for harsher conditions because there is a reduction in the area of the bare state region. The region of bistability is also reduced in this approximation. Therefore, it can be concluded that local spatial interactions increase the resilience of the system as compared to well-mixed system. This effect of local spatial interactions is the opposite of the effect of the demographic noise as shown in Fig. 3. The real system with both the local interactions and finite-size can show the dynamics resulting from the interplay between these two effects.