1 Introduction

One of the most prolific applications of the theory of dynamical systems lies in the field of neuroscience. At least partially, this is related to the fact that a single neuron can be understood and modeled as an electrical circuit with nonlinear feedback. On its own, it possesses a stable state of rest but may show a short-term large-scale deviation (spike) from this resting state if sufficiently stimulated, e.g., by incoming spikes from other neurons. This physiological property, commonly known as excitability, translates to the corresponding dynamical system being close to some limit cycle bifurcation [1]. In particular, class I excitability relates to a saddle-node homoclinic bifurcation [2] also known as a saddle-node bifurcation on an invariant circle. This bifurcation with normal form \({\dot{x}}=\epsilon +x^2\) is essentially a saddle-node bifurcation, but takes place on the extended real line \(\hat{\mathbf {R}}=\mathbf {R}\cup \{\infty \}\). For \(\epsilon <0\), the system possesses a stable equilibrium at \(x^\mathrm{s}=-\sqrt{-\epsilon }\) and an unstable one at \(x^\mathrm{u}=\sqrt{-\epsilon }\). At \(\epsilon =0\), it undergoes a saddle-node bifurcation after which the system becomes oscillatory: within the time \(\pi \,\epsilon ^{-1/2}\), x traverses the entire \(\hat{\mathbf {R}}\) by passing the point at infinity. For small negative \(\epsilon \), a sufficiently strong perturbation \(\delta x\) of the stable state \(x^\mathrm{s}\) (with \(\delta x>2\sqrt{-\epsilon }\)) traces in finite time the extended real line and comes back to \(x^\mathrm{s}\).

Two types of coupling between excitable units can, informally, be distinguished. One may speak of attractive coupling if two units at close distance to each other display, regardless of their position in the state space, a tendency to approach each other. On the other hand, if the contribution of coupling, taken alone, tends to increase the distance, it is natural to call the coupling repulsive.

If the identical excitable units are decoupled, there exists a stable collective equilibrium for the ensemble dynamics, with every element located at its state of rest. Attractive coupling binds these units stronger together, enhancing the stability of the collective equilibrium. In contrast, if some or all units are coupled repulsively, stability of the collective equilibrium is weakened or even gets lost, and non-trivial dynamics may arise [3,4,5,6,7]. In what follows, we focus on the case of exclusively repulsive coupling.

This paper consists of four parts. In Sect. 2, we discuss the notion of an active rotator that serves as one-dimensional representative of class I excitable elements. We also formalize the notions of attractive and repulsive coupling. In Sect. 3, we review previous results from [7]. The focus is put on families of systems that, for a suitable choice of parameters, feature a special type of partial integrability, known as the Watanabe–Strogatz (abbreviated below as WS) integrability [8, 9]. In particular, existence and stability of such robust periodic solutions as splay states and two-cluster states are concerned. The non-local transfer of stability between these states takes place when the system becomes WS-integrable. In Sect. 4 we briefly sketch the unfolding of non-locality in the bifurcation scenario in presence of additional governing parameters, providing a more general understanding of families of phase models. Finally, in Sect. 5, we present the example of an ensemble of coupled Morris–Lecar neurons [10] where numerical evidence confirms that the results obtained from active rotators pertain as well to ensembles of higher dimensional class I excitable units.

2 Ensembles of active rotators

We start by discussing the concept of an active rotator. Just prior to the homoclinic saddle-node bifurcation, asymptotic dynamics in the phase space is essentially one-dimensional: decay of disturbances to the stable state of rest occurs along either of two one-dimensional components (separatrices) of the unstable manifold of the unstable equilibrium. It is convenient to parametrize the latter manifold with a single coordinate. Since two equilibria and the separatrices form the closed contour, we view this coordinate as a phase-like variable (introduction of the proper phase is impossible in the context, involving the stable state of rest). Dynamics of this variable \(\phi \) obeys the equation \({\dot{\phi }}=f(\phi ,\delta )\) where \(\delta \) is the governing parameter; we set \(\delta =0\) at the value corresponding to the saddle-node homoclinic bifurcation. The sufficiently smooth function f is assumed to possess for \(\delta <0\) exactly two zeros \(f(\phi ^\mathrm{s},\delta )=f(\phi ^\mathrm{u},\delta )=0\) with \(f'(\phi ^\mathrm{s},\delta )<0\) and \(f'(\phi ^\mathrm{u},\delta )>0\), and for \(\delta >0\) no zeros whatsoever (here and in what follows, a prime denotes the derivative with respect to \(\phi \)). The zeros \(\phi ^\mathrm{s}\) and \(\phi ^\mathrm{u}\) are then the stable and unstable equilibria of the above equation, respectively. At \(\delta =0\), these two equilibria merge and disappear, so that a periodic motion of \(\phi \) emerges. Therefore, for sufficiently small negative \(\delta \), systems of the considered type are class I excitable. Commonly, they are known as active rotators [11].

Intrinsically related to other popular simple models of excitable neural cells like the QIF (quadratic integrate-and-fire) neurons and theta-neurons, active rotators have been intensively analyzed within the last decades. Along with different variants of dynamics of a single unit (that can be augmented by taking into account adaptation, see, e.g., [12]), much attention, starting from the original publication [11], has been paid to ensembles of coupled active rotators in the presence of noise [13,14,15,16]. Closer to our current context, interrelation between the Watanabe–Strogatz formalism and the existence of marginally stable splay states in ensembles of the pulse-coupled QIF neurons has been established in [17], whereas the derivation of a set of exact macroscopic equations for a network of spiking neurons and complete interpretation of ensemble dynamics in terms of the firing rate and the mean membrane potential has been performed in [18].

Below, we assume that the interaction between two active rotators \(\phi _i\) and \(\phi _j\) depends only on their mutual phase difference. Hence, it can be described by a coupling term of the form \(g(\phi _i-\phi _j)\). If the coupling function \(g:S^1\rightarrow \mathbf {R}\) possesses a zero at 0, we call it attractive if \(g'(0)<0\) and repulsive if \(g'(0)>0\).

We are interested in systems of N identical active rotators, coupled in such a way that the interaction (i) is pairwise, (ii) depends on the difference between the phases, (iii) is all-to-all, and (iv) is repulsive. Such a system can be described by the equation

$$\begin{aligned} {\dot{\phi }}_j = f(\phi _j,\delta ) + \frac{1}{N}\sum _{k=1}^{N}g(\phi _k-\phi _j), \end{aligned}$$
(1)

so that \(f(\phi _j,\delta )\) characterizes the on-site dynamics of the unit j and g determines the coupling within each pair of two such units. Systems like (1) have two general properties. First, the units cannot surpass each other. They preserve the order of the phases \(\phi _j\): if, at some time t, the ordering is fixed, e.g., as \(\phi _1\le \phi _2\le \cdots \le \phi _N<\phi _1+2\pi \), it holds for all times \(t'\). Equivalently, \(\phi _i(t)=\phi _j(t)\) at some t implies \(\phi _j(t')=\phi _j(t')\) for all \(t'\). We may therefore always assume the units to be ordered as above without loss of generality. Permutations of units lead to equivalent solutions for different ordering.

The second important property is that the system (1) possesses a synchronous subspace in which the instantaneous values of all phases coincide. Inside this subspace, the coupling terms vanish identically and every unit tends to its equilibrium value \(\phi ^\mathrm{s}\). The collective state of rest \(\varPhi ^\mathrm{s}=(\phi ^\mathrm{s},\dots ,\phi ^\mathrm{s})\) is stable if the coupling is attractive, since each unit is driven towards \(\phi ^\mathrm{s}\) not only by its on-site dynamics but by the other units, as well. However, \(\varPhi ^\mathrm{s}\) can be destabilized by sufficiently strong repulsive coupling [6].

The arguably simplest choice for a system of the type (1) was introduced by Shinomoto and Kuramoto [11] and is given by

$$\begin{aligned} {\dot{\phi }}_j = \omega - \sin \phi _j + \frac{\kappa }{N}\sum _{k=1}^N \sin (\phi _k-\phi _j). \end{aligned}$$
(2)

For \(|\omega |<1\), it yields an ensemble of active rotators, and repulsive coupling translates to the condition \(\kappa <0\). The starting point of our work was the observation, made in [6], that this system shows unconventional dynamics: a continuum of periodic orbits, each one possessing at least \(N-3\) neutrally stable directions. The reason for this lies in the fact that (2) fulfills conditions for the Watanabe–Strogatz integrability [8]. Being interested in the general properties of systems of excitable units, the question thus arises how generic the solutions found in [6] are.

3 Persistence and stability of splay states and 2-cluster states

In this section, we review some of the main results from [7]. As mentioned above, the dynamics of (2) is highly degenerate. The reason for this is the invariance of equations not only (obviously) with respect to permutations of the units, but also with respect to transformations forming a subgroup of the group of Möbius transformations [8, 9]. This degeneracy can be lifted in different ways. One option is to make the individual units non-identical, e.g., by introducing site-dependent parameters \(\omega _j\) or \(\kappa _j\). Another option is to couple each unit to a common field H via the second or higher order Fourier mode, i.e., perturbation terms of the form \(\epsilon \,h(\phi _j)=\epsilon \,H(\phi )\mathrm {e}^{ik\phi _j}+\text {c.c.}\) with \(k\ge 2\). The simple way to do so is by introducing perturbations in the on-site dynamics, so that the generalized model reads

$$\begin{aligned} {\dot{\phi }}_j=\omega -\sin \phi _j+\epsilon h(\phi _j) + \frac{\kappa }{N}\sum _{k=1}^{N}\sin (\phi _k-\phi _j), \end{aligned}$$
(3)

where

$$\begin{aligned} h(\phi )=\sum _{m=2}^{\infty } \left( a_m\sin m\phi + b_m\cos m\phi \right) , \end{aligned}$$
(4)

and \(\epsilon \) controls the deviation from the WS-integrable case \(\epsilon =0\). Since for the integrable case, all periodic solutions of the continuum observed in [6] possess neutrally stable directions, it cannot readily be assumed that any of these solutions persist.

However, from the infinitude of different periodic solutions of the system (2), reported in [6], two solutions stand out: splay states and 2-cluster states. In n-cluster solutions, the elements form n groups within which their instantaneous coordinates coincide.

A pure splay state of period T is a periodic solution of a system like (1) or (2) of the form \(\phi _j(t)=\psi \left( t-(j-1)\frac{T}{N}\right) \) for some T-periodic function \(\psi (t)\). Hence, all phases are equally staggered in time but not necessarily on the circle \(S^1\): for a general active rotator, the difference \(\phi _j(t)-\phi _k(t)\) is in general not a constant.

Variations of this pure splay state are possible. We call a periodic solution a clustered splay state of type (n, m) if the ensemble splits in n clusters of m units each, such that the cluster coordinates are equally staggered in time. Thus, a pure splay state is of the type (N, 1), while for a clustered splay state of, e.g., type (3, 2) and period T, the 6 units can be written as, e.g., \(\phi _1(t)=\phi _2(t)=\phi _A(t)\), \(\phi _3(t)=\phi _4(t)=\phi _B(t)\), and \(\phi _5(t)=\phi _6(t)=\phi _C(t)\), with \(\phi _A(t)=\psi (t)\), \(\phi _B(t)=\psi (t-T/3)\), and \(\phi _C(t)=\psi (t-2T/3)\) for an appropriate T-periodic function \(\psi \).

A special class of clustered splay states are those of type (2, N/2)Footnote 1, i.e., solutions that consist of two clusters A and B of equal size. As will become clear below, this special class differs significantly from other splay types, so that they deserve to be considered on their own.

Splay States In the ensemble (2), increase in the repulsion strength leads to the birth of the splay states and the clustered splay solutions at the threshold value \(\kappa _0=-\sqrt{1-\omega ^2}\), at which also the collective state of rest \(\varPhi ^s\) undergoes a transcritical homoclinic bifurcation [19], colliding with \(\sim 2^{N-1}\) saddle steady states [6]. The continuum of periodic solutions then arises through the fact that WS-integrability implies that the phase space \(T^N\cong S^1\times \dots \times S^1\) bears a \((N-3)\)-dimensional foliation into (generally) 3-dimensional submanifolds. As a consequence: the splay states are hyperbolic only w.r.t. the invariant submanifolds within which they exist. Moving to a sufficiently close neighboring submanifold induces a continuous change in the local vector field under which the periodic orbit (as normally hyperbolic manifolds) persists but is in general not a splay state anymore. This results in the formation of the continuum.

A consequence of WS-integrability is the existence of \(N-3\) functionally independent constants of motion [8]. These constants of motion correspond to the \((N-3)\)-dimensional foliation of the phase space.

For small \(\epsilon \ne 0\), the splay states are persistent. They become isolated hyperbolic periodic solutions, whose stability depends on the sign of \(\epsilon \). On the other hand, other periodic orbits in the immediate vicinity of these splay states are destroyed. However, the continuum seems to form an invariant manifold \({\mathcal {M}}\) which, by itself, persists for \(\epsilon \ne 0\) as well. Dynamics on \({\mathcal {M}}\) then looks as follows: the higher order terms of h introduce a slow drift term on \({\mathcal {M}}\) that results in a spiraling motion on it. A symmetry argument then implies that this drift cannot act indefinitely. Instead, the spiraling motion must converge towards some periodic orbits with high symmetry, such as splay states. For initial conditions that do not lie in \({\mathcal {M}}\), the spiraling motion is preceded by a fast convergence towards \({\mathcal {M}}\).

Two-cluster states Periodic oscillations of two clusters play a noticeable role in the asymptotic dynamics of (3). While for \(\epsilon =0\), all other (clustered) splay states can be understood within the framework of WS-integrability, the 2-cluster states form a separate case. The reason for this lies in the fact that the Watanabe–Strogatz formalism requires that the ensemble consists of at least three distinct clusters: only then the dimensional reduction to an equivalent 3-dimensional system, corresponding to the foliation of \(T^N\) in invariant 3-dimensional manifolds, can be achieved. As a consequence, 2-cluster states do not emerge through the transcritical heteroclinic bifurcation. Instead, they are formed in heteroclinic bifurcations or saddle-node homoclinic bifurcations that involve 2-cluster equilibria [7]. In this review, we focus on the exemplary case

$$\begin{aligned} {\dot{\phi }}_j=\omega -\sin \phi _j+\epsilon \sin 2\phi _j + \frac{\kappa }{N}\sum _{k=1}^N\sin (\phi _k-\phi _j),\qquad \end{aligned}$$
(5)

for simplicity. We note, however, that the discussed results can be extended to generic choices for \(h(\phi _j)\) in (4).

One of the main results in [7] is that the higher order Fourier modes in (3) determine the splitting stability of the 2-cluster states. Stability of clustered periodic solutions comes in two different flavors: stability against perturbations that leave clusters whole (in what follows called non-splitting) or against perturbations that split single phases from one cluster (in what follows called splitting) [20]. Thus, a non-splitting perturbation moves one or several clusters as a whole, while splitting perturbations are those that dissolve one cluster with the condition that its “center-of-mass” is preserved.

For systems like (3), there occurs a switch of stability w.r.t. splitting perturbations for periodic 2-cluster states at \(\epsilon =0\) and for general h as long as both clusters are of equal size. For example, in (5), these periodic states are stable for small \(\epsilon <0\) and unstable for small \(\epsilon >0\). Transition for the splay states goes in the opposite direction: being stable for \(\epsilon >0\), they become unstable for \(\epsilon <0\). Like for the splay states, we observe that a randomly chosen initial state \(\phi \in {\mathcal {M}}\) close to the periodic 2-cluster state slowly evolves either towards this orbit or away from it, depending on the asymptotic stability of the 2-cluster state.

However, if the numbers of units in two clusters differ, the picture changes dramatically. Let the Floquet multipliers \(\varLambda ^A\) and \(\varLambda ^B\), respectively, characterize the splitting stability of the clusters A and B. Then, at \(\epsilon =0\), the identity

$$\begin{aligned} \varLambda ^A\varLambda ^B=1, \end{aligned}$$
(6)

holds for any periodic 2-cluster state. In fact, this result generalizes to arbitrary WS-integrable systems. An immediate consequence of (6) is that for the equal size clusters A and B are of equal size, it follows \(\varLambda ^A=\varLambda ^B=1\): neutrality on the verge of the stability change. On the other hand, if A and B are of different sizes, \(\varLambda ^A\ne \varLambda ^B\) and thus one cluster [in case of (2) the smaller one] must be stable towards splitting perturbations, while the other (the larger one) is unstable. In particular, these clustered oscillatory states are not part of the continuum of orbits at \(\epsilon =0\); they are hyperbolic, i.e., isolated. States, consisting of two unequal clusters, are always asymptotically unstable in an open neighborhood of \(\epsilon =0\); for fixed ensemble size N, one can always choose \(\epsilon \ne 0\) sufficiently small, such that only 2-cluster states of equal cluster size can be stable. Growth of \(|\epsilon |\) for negative \(\epsilon \) leads to stabilization of unequal oscillatory clusters. For sufficiently large N, stability regions for these states form in the parameter space a nested pattern: for example, on the parameter plane of the ensemble with 100 units, the stability region of the state with periodic clusters of the sizes 53 and 47 lies inside the stability domain of the state with cluster sizes 52 and 48 which, in its turn, is located within the stability region of the state with cluster sizes 51 and 49 [7]. The more A and B differ in size, the larger \(|\epsilon |\) and \(|\kappa |\) must be chosen to suppress splitting.

Analysis, performed in [7], was restricted to one-parameter families of ensembles of active rotators that included the parameter value corresponding to the Watanabe–Strogatz integrability. Such families are degenerate: a generic family of dynamical systems, describing the ensembles of active rotators, nowhere features the WS-integrability. A consequence of the degeneracy is the unusual transition, reported in [7]; the non-local exchange of stability between the splay states and the two-clustered oscillations. Below, we extend the analysis to two-parameter families of dynamical systems. Within this framework, the non-local transition is unfolded into conventional bifurcation scenarios, involving the pitchfork and the saddle-node bifurcations of oscillatory states.

4 Circumventing the point of WS-integrability

The space \(H=\text {span}\left( \{\sin m\phi , \cos n\phi \}_{m,n\ge 2}\right) \) of perturbation functions h in (3) is of infinite dimension. The point \(\mathbf {0}\in H\) corresponds to the WS-integrable model (2). Varying the value of \(\varvec{\epsilon }\) in (3) renders a path \(\varGamma \) in H through the point \(\mathbf {0}\) where both the splay states and the 2-cluster states, change stability simultaneously. However, for active rotators augmented by high-order Fourier modes, a generic path through the parameter space does not contain the origin: the Watanabe–Strogatz point \(\mathbf {0}\). Hence, the question arises how, for such generic paths, stability of splay states and 2-cluster states are related to each other.

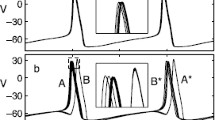
Clustered splay states of any type (n, m) feature in general two different types of (discrete) symmetry. The first one is symmetry under permutations within each cluster: since all units are identical, interchanging any two units j and k of one cluster (i.e., when \(\phi _j=\phi _k\)) leads to an equivalent state. The second symmetry is a spatio-temporal one: let the index \(\alpha \in \{1,\dots ,n\}\) enumerate the clusters \(A_n\) of the state (so that, e.g., \(\phi _1=\dots =\phi _m=\phi _{A_1}\) belong to cluster \(A_1\)) then shifting \(t\rightarrow t-T/n\) together with shifting each index \(j\rightarrow j+m\) leads again to an equivalent state. Clustered Splay states of different types (n, m) and \((n',m')\) then feature different symmetry groups. We expect that stability should be transferred between clustered splay states by means of families of periodic solutions with broken symmetry, existing within bounded parameter intervals. Consider the example of \(N=4\) units, where only pure splay states (i.e., \((n,m)=(4,1)\)) and 2-cluster states (i.e., \((n',m')=(2,2)\)) can exist. A transfer of stability occurs via periodic states that are “almost splays” at the bifurcation of splay states, and then evolve into “nearly 2-clusters” when they approach the periodic 2-cluster state. In doing so, these periodic states share neither of the symmetries of the splay or the 2-cluster state and are thus of lower (or broken) symmetry. An appropriate bifurcation that lowers the symmetry of a periodic solution is the pitchfork bifurcation (“symmetry crisis”). Since both types of the pitchfork—the super- and the subcritical ones—are possible in this situation, there are several variants of the overall bifurcation scenario. We sketch the basic ones in Fig. 1.

Fig. 1
figure 1

Schematic depiction of bifurcation scenarios for periodic orbits along the path \(\varGamma (s)\) through the parameter space. Here, s denotes the generic parameterization along the path. Pitchfork bifurcations of the splay solution and of the periodic clustered state occur at \(s_1\) and \(s_2\), respectively; the value \(s_3\) in the b denotes the saddle-node (fold) bifurcation of periodic solutions. Green: splay states; orange: 2-cluster states; black: mixed states with broken symmetry. Solid curves represent stable periodic orbits, while the dashed curves show the unstable ones. a Both pitchfork bifurcations at \(s_1\) and \(s_2\) are supercritical; pairs of stable broken symmetry states transfer stability between them. This scenario occurs, e.g., in Eq. (7) for \(\omega =0.6\) and \(\kappa =-0.85\). b A combination of two different types of pitchfork bifurcations; is observed, e.g., for \(\omega =0.6\) and \(\kappa =-1.25\) in Eq. (7). Here, before the basic states change stability, two pairs of broken symmetry states emerge in saddle-node bifurcations at \(s_3\). c both pitchfork bifurcations at \(s_1\) and \(s_2\) are subcritical; all mediating broken symmetry states are, in this case, unstable. This scenario takes place, e.g., in the ensemble of coupled Morris–Lecar neurons (see Sect. 5 below)

Full size image

For an illustration, we restrict ourselves to the perturbation of the WS-integrability that includes two linearly independent second-order Fourier modes in the on-site dynamics: we consider the model

$$\begin{aligned} {\dot{\phi }}_j&= \omega -\sin \phi _j + \epsilon ^s\sin 2\phi _j + \epsilon ^c\cos 2\phi _j \nonumber \\&\quad + \frac{\kappa }{N}\sum _{k=1}^N\sin (\phi _k-\phi _j). \end{aligned}$$
(7)

Let the vector \(\varvec{\epsilon }=(\epsilon ^\mathrm{s},\epsilon ^\mathrm{c})\) parameterize the perturbation. At \(\epsilon ^\mathrm{c}=0\), Eq. (7) turns into the model (5); therefore, \(\varvec{\epsilon }_1=(\epsilon ^\mathrm{s},0)\) yields stable periodic 2-cluster solutions for small negative \(\epsilon ^\mathrm{s}\) and unstable ones for small \(\epsilon ^\mathrm{s}>0\), while for splay states, the opposite holds. Similar behavior has been found for \(\varvec{\epsilon }_2=(0,\epsilon ^\mathrm{c})\) when \(\epsilon ^\mathrm{c}\) has been varied. This suggests that if both \(\epsilon ^\mathrm{s}\) and \(\epsilon ^\mathrm{c}\) have the same sign, the stabilizing or destabilizing effects of both perturbation terms sum up. On the other hand, a change of stability for given \(\omega \) and \(\kappa \) must occur for some \(\epsilon ^\mathrm{s}\cdot \epsilon ^\mathrm{c}<0\). We take an exemplary path that, on the plane spanned by \(\epsilon ^\mathrm{s}\) and \(\epsilon ^\mathrm{c}\), which connects by a straight line the points \(\varvec{\epsilon }_1=(1/20,0)\) and \(\varvec{\epsilon }_2=(0,-1/20)\): \(\varGamma (s)=s\varvec{\epsilon }_1+(1-s)\varvec{\epsilon }_2\). The path avoids \(\mathbf {0}\).

Along the exemplary path, the splay state changes stability at some \(s_1\in (0,1)\), while the 2-cluster state changes stability at some \(s_2\in (0,1)\). In case of the 2-cluster states, \(s_2\) does not depend on N [7]. For splay states, dependence of \(s_1\) on N is less transparent, and we restrict ourselves to \(N=4\): the minimal ensemble size that allows both the 2-cluster solutions and the splay states.

Fig. 2
figure 2

Existence and stability of splay states and periodic 2-cluster states for Eq. (7) with \(\omega =0.6\) and \(N=4\) along the path \(\varGamma (s)=s\varvec{\epsilon }_1+(1-s)\varvec{\epsilon }_2\). In Region I, neither splay states nor periodic 2-cluster states exist. Splay states emerge via the transcritical heteroclinic bifurcation of the collective state of rest at the left border of Region I. Periodic 2-cluster states emerge in double saddle-node homoclinic bifurcations at the left borders of Regions II and VI, respectively. In the Regions III and VI, splay states are stable, while 2-cluster states are either unstable (Region III) or non-existent (Region VI). At the border between the Regions III and IV, respectively, the Regions II and VI, the splay states lose stability in supercritical pitchfork bifurcations from which pairs of stable states with broken symmetry emerge. These broken symmetry states either disappear in a further supercritical pitchfork with the 2-cluster states ([cf. (a) in Fig. 1] at the border between the Regions IV and V, or, instead, vanish in the saddle-node bifurcations with additional unstable states with broken symmetry at the border between the Regions IV and VII. The latter states are born in subcritical pitchforks of the 2-cluster states at the border between the Regions V and VII; they exist only in the Region VII [cf. (b) in Fig. 1]. At the point in which the Regions IV, V, and VII meet, the pitchfork bifurcation of the 2-cluster states changes its type from sub- to supercritical. The overall result is a transfer of stability between splay states and periodic 2-cluster states

Full size image

As expected, we observe that stability is transferred between the splay state and the 2-cluster oscillatory state via the via the mediation of periodic solutions with broken symmetry.

To understand these scenarios, we note that, as long as the path \(\varGamma \) lies sufficiently close to \(\mathbf {0}\), hyperbolicity of the invariant manifold \({\mathcal {M}}\) guarantees that the dynamics essentially takes place on \({\mathcal {M}}\) for all \(\varGamma (s)\). Indeed, broken symmetry states are elements of the ensemble of continuous orbits at \(\mathbf {0}\) and so are natural candidates for persistent states. Within this picture, \({\mathcal {M}}\) apparently always contains splay and 2-cluster states as closed orbits, while for suitable paths through H, additional periodic orbits must detach and merge again with them. By symmetry, these orbits must always emerge pairwise, in full accordance to the numerical evidence.

For \(N=4\), the broken symmetry orbits of period \(T(\omega , \gamma , \kappa )\) can be characterized as follows: in contrast to a 2-cluster state in which the ensemble is comprised of two clusters A and B with, e.g., \(\phi _1(t)=\phi _2(t)=\phi _A(t)\) and \(\phi _3(t)=\phi _4(t)=\phi _B(t)\) where \(\phi _A(t)=\phi _B(t+T/2)\); we now have \(\phi _{1,2}(t)=\phi _A(t\pm \varDelta t/2)\) and \(\phi _{3,4}(t)=\phi _B(t\pm \varDelta t/2)\). In other words, the broken symmetry state is comprised of two groups of two units each. The groups are still separated by the half-period in time, whereas units inside them are separated by some time difference \(\varDelta t\) in their evolution. Increase of \(\varDelta t\) from 0 (at the first pitchfork) to T/4 (by the time of the second pitchfork) transforms the broken symmetry state continuously from the pure 2-cluster state into the pure splay state.

5 Ensembles of Morris–Lecar neurons

The well-known formalism of Kuramoto [21] allows to reduce dynamics in a set of weakly coupled oscillators to the phase description; dynamics of the ensemble is adequately reproduced by an appropriate set of phase oscillators. This approach works regardless of the dimension of the phase space of the individual oscillator, provided that there is a timescale separation between one slow variable (phase) and the remaining fast ones (amplitude). While (class I) excitable units lack an intrinsic phase, since they do not oscillate on their own, one might expect a similar connection to hold between the class I excitable units and the active rotators provided that the invariant circle for the single excitable unit is normally hyperbolic. Hence, for suitably small coupling strengths, a similar reduction to phase-like variables yields a system, akin to (3), which for small \(|\epsilon |\) would give rise to an invariant manifold \({\mathcal {M}}\), together with embedded periodic orbits.

It is therefore reasonable to look in ensembles of higher dimensional excitable units for collective states and transitions, similar to the ones, described in Sect. 4. Here, we take as an example the ensemble of the so-called Morris—Lecar neurons.

The Morris–Lecar model was originally introduced to describe neuro-physiological properties of giant barnacle muscle fibers [10]. It characterizes the properties of the cell in terms of the membrane voltage V of the fiber together with the normalized conductance w of the cell membrane for \(\text {K}^+\)–ions which acts as a slow recovery variable. In the context of our studies, the Morris–Lecar model is of particular interest, because its parameters can be tuned to yield class I excitability. Our set of parameters, shown in Table 1, is a variation of the standard choice from [22]. For our purposes, we consider a system of \(N=4\) Morris–Lecar neurons, coupled all-to-all via their respective mutual differences in the membrane voltages \(V_i\). The governing equations read

$$\begin{aligned}&C\,{\dot{V}}_i =\; g_{\mathrm{Ca}}\,n_{\infty }(V_i)\cdot (V_{\mathrm{Ca}}-V_i) -g_{\mathrm{K}}\,w_i\cdot (V_{\mathrm{K}}+V_i)\nonumber \\ \end{aligned}$$
(8)
$$\begin{aligned}&~~~~~~~~~-g_{\mathrm{L}}\cdot (V_{\mathrm{L}}+V_i) + I_{\mathrm{app}} + \frac{\kappa }{N}\sum _{j=1}^N (V_j - V_i)\nonumber \\&{\dot{w}}_i = \lambda (V_i)\cdot \left( w_{\infty }(V_i) - w_i\right) , \end{aligned}$$
(9)

where \(n_{\infty }(V) = \frac{1}{2}\left( 1+\tanh \frac{V-V_\mathrm{a}}{V_\mathrm{b}}\right) \) and \(w_{\infty }(V)=\frac{1}{2}\left( 1+\tanh \frac{V-V_\mathrm{c}}{V_\mathrm{d}}\right) \) describe the ratio of open Ca\(^{2+}\)–ion channels and the voltage-dependent maximum ratio of K\(^+\)-ion channels, respectively. While the former channels react to voltage changes instantaneously, the latter have finite V-dependent inverse recovery time \(\lambda (V)=\lambda _0\cosh \frac{V-V_\mathrm{c}}{V_\mathrm{e}}\).

The perturbation terms in (3) act on the second-order or higher order Fourier modes of the on-site dynamics while leaving the zeroth- and first-order term invariant along the path \(\varGamma (s)\), with \(s\in [0,1]\). One can achieve a somewhat similar behavior for the ensemble of Morris–Lecar neurons by scaling the conductances \(g_{\text {Ca}}\), \(g_{\text {K}}\), and \(g_{\text {L}}\) by a common factor \((1+s)\), i.e., \(g_x\mapsto (1+s)\cdot g_x\). This rescaling on its own affects all terms in the Taylor expansion of the r.h.s. of (8) \({\dot{V}}_j=-a_0+a_1V_j+{\mathcal {O}}(V_j^2)\). However, the current I only enters the term \(a_0\) and can be absorbed by a suitable rescaling of the \(V_i\). Hence, if we rescale \(V_j\), such that \({\dot{V}}_j=a_0(s, I)) + V_j + {\mathcal {O}}(V_j)\), we can always choose I, such that \(a_0\) is constant along \(\varGamma \). The necessary condition for this is that the ratio of coefficients \(a_0/a_1\) is kept constant which yields the relation

$$\begin{aligned}&\frac{\frac{1}{\gamma }I-g_{\mathrm{L}}V_{\mathrm{L}} - \frac{1}{2}g_{\mathrm{Ca}}V_{\mathrm{Ca}}\left( \tanh \frac{V_1}{V_2}-1 \right) }{-g_{\mathrm{L}} + \frac{1}{2}g_{\mathrm{Ca}}\left( \tanh \frac{V_1}{V_2}-1 + \frac{V_{\mathrm{Ca}}}{V_2}\left( 1-\tanh \frac{V_1}{V_2}\right) \tanh \frac{V_1}{V_2}\right) }\nonumber \\&\quad = \mathrm const, \end{aligned}$$
(10)

through which the appropriate value of I is determined.

Varying s and \(\kappa \), we look again at the existence of the splay and 2-cluster states and at the transfer of stability between them. Results are depicted in Fig. 3.

Fig. 3
figure 3

Existence and stability of splay and periodic 2-cluster states for \(N=4\) globally coupled Morris–Lecar neurons (8) and (9). In Region I, neither splay states nor periodic 2-cluster states exist. The splay states exist to the left of the border between the Regions II and IV and to the left of the border between V and VI. The periodic 2-cluster states emerge at the left border of the Region I. In the Region III, the splay states are unstable, while 2-cluster states are stable. At the border between III and IV, the splay states get stabilized by a subcritical pitchfork in which two unstable broken symmetry states emerge and persist in the Regions IV and II. At the borders between the Regions IV and V as well as between the Regions II and VI, these broken symmetry states vanish in another subcritical pitchfork with the periodic 2-cluster state, rendering the latter unstable in the Regions V and VI, whereas it is stable in the Regions II, III, and IV. This corresponds to the bifurcation scenario, sketched in the (c) of Fig. 1. The 2-cluster states emerge in heteroclinic bifurcations to the left from the Region I, whereas the splay states exist in the Regions III, IV, and V. The result is a transfer of instability between splay states and periodic 2-cluster states

Full size image

It turns out that the ensemble of Morris–Lecar neurons at these parameter values is, in a sense, complementary to the model of phase oscillators discussed in the preceding section: whereas the bifurcation scenarios in the phase model match the panels (a) and (b) in Fig. 1, bifurcations in the Morris–Lecar ensemble correspond to the scenario sketched in panel (c). For both types of the basic temporal patterns, the clustered states and the splay, the pitchfork bifurcations are subcritical. Therefore, the states with broken symmetry transfer not stability but, rather, instability between them. Altogether, these numerical findings further support the assertion that the results from the phase model (5) generalize to systems of higher dimensional class I excitable units.

6 Conclusions

One of the key concepts in the description of neurons is excitability. Class I excitability translates to a dynamical system, being close to a saddle-node homoclinic bifurcation. The arguably simplest dynamical system which possesses this feature is the active rotator. Ensembles of identical active rotators, sinusoidally coupled all-to-all can, for sufficiently repulsive coupling, yield oscillatory ensemble dynamics.

In this work, we reviewed previous results concerning two important types of generic collective oscillatory solutions: the splay states and the periodic 2-cluster states. The former is characterized by its constituents being equally staggered in time, while in the latter case, the ensemble splits into two distinct clusters, which are then equally staggered in time. In the general context of coupled oscillators, transitions between the splay and clustered states have been studied, e.g., in [23] for delay coupled Stuart–Landau oscillators, as well as in [24] for oscillators with adaptive coupling coefficients. As we have seen above, clustered oscillations and splays in ensembles of globally coupled active rotators have their peculiarities. While splay states or clustered variations thereof emerge in a transcritical heteroclinic bifurcation, 2-cluster states are born in global bifurcations involving pairs of 2-cluster states of equilibrium. Respective stabilities of these two states are closely related. Varying system parameters, both periodic states switch their stability simultaneously if, at the transition, the system becomes Watanabe–Strogatz integrable. The underlying reason for this is that both orbits lie within a stable invariant manifold that, at the point of integrability, is comprised of a continuous family of periodic orbits. If the system is not integrable, dynamics on the manifold look like a spiraling motion towards one of the persistent periodic orbits. Under a generic variation of parameters, the system does not become integrable, but periodic orbits still exchange their stability. We have illustrated how the transfer of stability between 2-cluster and splay states is mediated by periodic states with broken symmetry. These broken symmetry states emerge in pitchfork bifurcations involving either the splay or the 2-cluster states. The result is a generic local exchange of stability instead of the unconventional non-local one.

The fact that ensembles of voltage-coupled Morris–Lecar neurons essentially show the same bifurcation scenarios allows us to suggest that this transfer of stability is a generic feature of similar ensembles of class I excitable units.

Table 1 Parameters of the Morris–Lecar model that yield class I excitability
Full size table

The two discussed types of periodic orbits are neither the only possible periodic solutions for systems of coupled excitable units, nor the only possible attractors. Nevertheless, many of these other possibly stable candidates can be understood as “imperfect” variations of splay or 2-cluster states, i.e., as solutions where the clusters are not of exactly equal size. For an imperfect realization of a splay, the time intervals for two consecutive clusters to make a turn around the circle are not identical anymore. However, as long as the variation in cluster size is small, these states are comparable in their properties to real clustered splay states.

Stability of imperfect periodic 2-cluster states for the phase model can be understood in terms of Watanabe–Strogatz integrability. We have shown that for every WS-integrable model, such states always consist of one stable and one unstable cluster. Perturbations that make the system non-integrable inherit this property as long as the perturbation is small. This, further, results for sufficiently large N in the nested pattern of stability regions in the parameter space [7]. Additionally, this implies that these imperfect 2-cluster states are not embedded in the invariant manifold that, in the integrable case, consists of the continuum of periodic orbits.

Our analysis has been restricted to purely sinusoidal coupling between the identical units in the ensemble. In general, introduction of higher Fourier harmonics into the coupling disables the Watanabe–Strogatz dynamics [9] (save for the cases the where every unit couples solely to all global fields by a single higher harmonic [25, 26]). In contrast, structurally stable solutions, like the splay states and the clustered oscillations survive modification of the coupling, and the discussed scenarios of stability transfer between them stay relevant also for non-sinusoidal interaction