1 Introduction

Some of the first observations of the phenomenon of synchronization have been made in the late seventeenth century. The Dutch physician Kaempfer observed a swarm of fireflies in Asia and noted their rhythmic flashing; their lights appeared in a regular interval all over the whole swarm [1]. Some years earlier, the Dutch physicist Huygens already noted that two pendulum clocks, fastened to the same beam, always swung in opposite directions, regardless of where and how he released them [2].

Despite essential progress, synchronization remains a topic of active research. In particular, many studies are devoted to the investigation of different partially synchronous states. Partial synchrony describes the state between full synchrony and asynchrony, where not all phases or frequencies are equal. In most systems, partial synchrony exists in the biggest part of the parameter space, making it an important topic to study. Some interesting realizations of partial synchronous states are the chimera [3], Bellerophon [4], traveling wave [5], or solitary state [6].

The study of self-sustained oscillations has become an important tool to describe phenomenons as diverse as the common movement of pedestrians on a bridge [7], the heart beat [8] or the motion of a fish swarm [9] and their synchronization properties. The application to neuroscience, where oscillatory behavior determines the dynamics in the brain [10,11,12], is of special interest.

Self-sustained oscillators are well understood, but a quantitative analysis of systems of coupled oscillators is generally hard. The description of oscillatory systems can consist of numerous coupled differential equations containing nonlinear terms and only allows for approximate or qualitative analysis in most cases. One way to reduce the complexity is phase reduction, which describes every single oscillatory unit with one one-dimensional variable, thereby reducing the problem’s dimensionality.

The phase reduction of a single oscillator is known analytically only for a few types. Even for these types of oscillators, coupled units’ dynamics are typically only available in the weak coupling limit, i.e., in the first order of the coupling strength. Methods for finding the phase dynamics for stronger couplings are either restricted to coupling functions with a specific property [13] or to specific systems [14].

While the first-order phase approximation of pairwise coupled oscillators yields only terms depending on two phases, beyond the weak coupling limit, generally terms depending on several phases appear. Some of these new terms are triplet terms or non-structural terms, i.e., connections not present in the coupling scheme [14, 15]. These are often reconstructed numerically but are seen as spurious terms or correlations.

In this minireview, I summarize the current state of research for my Ph.D. thesis by analyzing three cases of partial synchrony with the help of phase dynamics in increasing levels of complexity. In the first level in Sect. 2.1, the macroscopic phase dynamics of a complex mean-field oscillator, generated by the collective dynamics of the single units, is investigated. The novel results about the direct extension of the phase from a single oscillator to an ensemble of oscillators are shown via the collective phase response curve (PRC) for the mean-field. It measures the mean-field’s reaction to a perturbation of the oscillators in the first order of the perturbation strength and is applied to coupled Rayleigh oscillators. In the second level, a more sophisticated approach, the weak coupling limit, is used to describe the phases of the units in the first order of the coupling strength. In the Kuramoto model [16], this approach is used widely to investigate synchronization. Here it is applied to two groups of oscillators, one attractive and one repulsive, to investigate an interesting solitary state in Sect. 3.1, and summarizes the paper [17]. Finally, in Sect. 3.2, the phase reduction is expanded past the weak coupling limit, as the third level of complexity, in a system of Stuart-Landau oscillators using a perturbation method, as described in [18]. This approach reveals additional terms in the phase model. For example, triplet terms appear for pairwise coupled oscillators.

2 Phase dynamics

Phase dynamics are defined for an oscillatory dynamical system of arbitrary dimension

$$\begin{aligned} \frac{d \varvec{y}}{dt} = \varvec{f}(\varvec{y}), \end{aligned}$$
(1)

with a stable limit cycle of period T in the state space \({\varvec{Y}(t + T) = \varvec{Y}(t)}\). On this limit cycle, and in its basin of attraction, a phase \({\varphi = \Phi (\varvec{y})}\) can be defined that identifies the state uniquely and grows uniformly in time by

$$\begin{aligned} {\dot{\varphi }} = \omega = \frac{\partial \Phi }{\partial \varvec{y}} \varvec{f}(\varvec{y}), \end{aligned}$$
(2)

with a frequency of \({\omega = \frac{2 \pi }{T}}\) [2]. This phase reduces the dimensionality of the dynamics to just one. For most types of oscillators the phase dynamics are not known analytically and have to be reconstructed numerically.

In Eq. (2) only the autonomous dynamics are considered. In the case of a weak perturbation the phase instead evolves according to the Winfree Eq. [19] in the first order of the perturbation strength P. With the PRC \(\Delta \) and the perturbation p it reads

$$\begin{aligned} {\dot{\varphi }} = \omega + \Delta (\varphi ) p(t) + {\mathcal {O}}(P^2)\; . \end{aligned}$$
(3)

The PRC \(\Delta \) describes the phase change depending on the current phase. It is also an important tool in describing the system beyond the phase dynamics, as its form gives information about the stability and synchronization properties of the system [20].

2.1 Phase dynamics of a macroscopic oscillator—rayleigh model

A natural extension of the PRC in the case of multiple oscillators is the collective PRC, which describes the reaction of a whole ensemble of N oscillators to a perturbation. Their dynamics are measured by their average, the mean-field \({\varvec{Z} = 1/N \sum _j \varvec{y}_j}\). For a strong enough coupling, the mean-field will also move on a limit cycle, and a perturbation of the oscillators will lead to a deviation from its stable trajectory. This means the mean-field can be seen as a complex oscillator, as demonstrated for the brain rhythm in experiments with rats [21]. From the reaction of the mean-field oscillator, it is even possible to gain information about the PRC of single oscillators [22].

Whereas the PRC \(\Delta \) describes the complete reaction to a perturbation, the collective PRC can be split into two parts. The prompt PRC \(\Delta _0\) is the immediate reaction of the mean-field and the relaxation PRC \(\Delta _r\) the part that describes the relaxation of the oscillators after the perturbation and the resulting change in their distribution. Together these form the final PRC \(\Delta _f\) [23, 24]. Formally this can be written as

$$\begin{aligned} \Delta _0(\varphi _0)&= {\bar{\varphi }}_0 - \varphi _0 \; , \end{aligned}$$
(4)
$$\begin{aligned} \Delta _f(\varphi _0)&= \lim _{t \rightarrow \infty } ({\bar{\varphi }}(t - \tau ) - \varphi (t - \tau )) \nonumber \\&= \Delta _0(\varphi _0) + \lim _{t \rightarrow \infty } \Delta _r(\varphi _0, t - \tau ) \; , \end{aligned}$$
(5)

where \(\tau \) is the time of the perturbation, \(\varphi _0\) is the phase at the time of perturbation of the unperturbed system and \({\bar{\varphi }}\) the phase in the perturbed system. Because there does not exist a general way to describe the dynamics of the mean-field, the collective PRC and its parts have to be calculated numerically.

Numerically the collective PRC is found by measuring the change in the k-th period of the mean-field after the perturbation \({\bar{T}}_k\) and the unperturbed period T as

$$\begin{aligned} \Delta _N(\varphi _0) = 2 \pi \sum _{j=1}^N \frac{T - {\bar{T}}_k}{T} \; . \end{aligned}$$
(6)

After a sufficiently long time this will approach the final PRC in Eq. (5).

Consider a system of N coupled Rayleigh oscillators [25] with the dynamics

$$\begin{aligned} \ddot{x}_k - \eta (1 - {\dot{x}}_k^2) {\dot{x}}_k + \omega _k^2 x_k = \varepsilon ({\dot{X}} - {\dot{x}}_k) \; . \end{aligned}$$
(7)

The \(\eta \) is a nonlinearity parameter, \(\varepsilon \) the coupling strength and \({{\dot{X}} = 1/N \sum _j {\dot{x}}_j}\). The natural frequencies \(\omega _k\) are distributed according to a Gaussian distribution with mean 1 and standard deviation 0.01. For \(\eta = 6\) and \({N = 500}\) this system has a stable limit cycle of the mean-field for \({\varepsilon > rapprox 0.134}\) and is in the partial synchronous regime.

Fig. 1
figure 1

The collective PRC \(\Delta _{100}\) for the Rayleigh model in Eq. (7) with perturbation strength P is shown in (a). The black dots mark the PRC of the single oscillator and the lines the numerically measured values for \(\varepsilon \in \{0.134, 0.336, 0.538, 0.74, 0.942\}\), where the collective PRC approaches the single oscillator PRC with increasing \(\varepsilon \). In (b) the method for the calculation of the synchronization time \(t_{\text {sync}}\) is visualized. The timescales for the synchronization and the relaxation are shown in (c). The black dots denote the magnitude of the limit cycle at the crossing of the positive \({\dot{x}}\)-axis, the green crosses \(t_{\text {sync}}\) and the red triangles \(t_{\text {relax}}\). The necessary \(\varepsilon \) for a stable limit cycle is marked with a black line

Full size image

The oscillators are perturbed simultaneously in the \({\dot{x}}\)-direction with a small enough strength P, such that the collective PRC scales linearly with P and Eq. (3) is valid. The resulting response of the mean-field is shown in Fig. 1a. While the collective PRC is flat for small \(\varepsilon \), it approaches the PRC of a single oscillator with increasing coupling strength. The approach to the PRC of a single oscillator is the expected outcome, as in the case of \(\varepsilon \rightarrow \infty \), the oscillators will be fully synchronized and behave like a single unit.

An important property of the collective PRC is the needed relaxation time \(t_{\text {relax}}\), as the application to real-world noisy systems becomes impossible if it is too long. When the oscillators are perturbed strongly before they fully relax, then the mean-field will not reach its limit cycle, and the phase dynamics in Eq. (3) are not applicable. To have a comparable timescale consider the synchronization time \(t_{\text {sync}}\) in Fig. 1b. It is measured as a linear approximation of the time needed to reach the stable distribution of oscillators, given by \(R = \left| {\varvec{Z}} \right| \approx const\), from a splay state, where all oscillators are distributed uniformly in the phase. The slope for the linear approximation is chosen as the value at the inflection point, i.e., the biggest \({\dot{R}}\). A comparison of the time scales in Fig. 1c shows that \(t_{\text {relax}}\) (at about 40T) is longer than \(t_{\text {sync}}\). This suggests a very weak attraction to the stable distribution. The collective PRC can thus be only applied in an approximate sense.

3 Phase dynamics of coupled oscillators

After investigating the phase dynamics under the influence of a perturbation, the next step of abstraction is the application of phase dynamics to coupled oscillators. Instead of the mean-field, the interest lies now on the single oscillatory units and their phases. The dynamics of coupled oscillators with coupling function \(\varvec{G}_k\) for oscillator k and coupling strength \(\varepsilon \) are

$$\begin{aligned} \frac{d \varvec{y}_k}{dt} = \varvec{f}_k(\varvec{y}_k) + \varepsilon \varvec{G}_k(\varvec{y}_1, \varvec{y}_2, \ldots ) \; . \end{aligned}$$
(8)

The phase dynamics for such a system are given analogous to Eq. (2) with \({\varphi _k = \Phi _k(\varvec{y}_k)}\) as

$$\begin{aligned} {\dot{\varphi }}_k = \omega _k + \varepsilon \frac{\partial \Phi _k}{\partial \varvec{y}_k} \varvec{G}_k (\varvec{y}_1, \varvec{y}_2, \ldots ) \; . \end{aligned}$$
(9)

In this case, the phase does not grow uniformly. While it could be found on the limit cycle by virtue of the period, now the phases of all points in the state space have to be known to solve the coupling term. With the approximation of weak coupling, the dynamics stay close to the limit cycle of the uncoupled unit and the phases in this region are known, so the coupling function can be written in terms of these phases

$$\begin{aligned} {\dot{\varphi }}_k = \omega _k + \varepsilon G_k(\varphi _k, \varphi _1, \varphi _2, \ldots ) + {\mathcal {O}}(\varepsilon ^2) \; . \end{aligned}$$
(10)

Higher-order approximations have to be considered to extend the phase dynamics farther past the limit cycle, for example, when considering higher coupling strengths.

Some methods for analytical phase reduction of higher-order consider systems with a separation of timescales [13, 26] or use isostable coordinates [27]. A general method that only works for systems with a known phase in the autonomous systems uses a perturbation Ansatz on the isochrones [14]. To reconstruct the phase dynamics numerically, one typically uses a Fourier series to represent the coupling function and then fits the coefficients using, e.g., a multiple shot [28] or Bayesian methods [29]. Other numerical reductions include reconstruction of the phase from a polar phase that is determined by a Hilbert transformation [30, 31] or directly with an iterative Hilbert transform [32]. Some improvements can be made by using absolute phases in the coupling function instead of phase differences [33] or considering triplets of oscillators to find structural connectivity [34].

3.1 Weakly coupled oscillators—Kuramoto model

The Kuramoto model [35, 36] describes a weakly pairwise all-to-all coupled system of oscillators. The first order approximation in Eq. (10) is valid and the dynamics can be written as

$$\begin{aligned} {\dot{\varphi }}_k = \omega _k + \frac{\varepsilon }{N} \sum _{j = 1}^N \sin (\varphi _j - \varphi _k + \alpha _k) \; . \end{aligned}$$
(11)

The \(\omega _k\) are the natural frequencies and the \(\alpha _k\) the phase shift parameters.

By using the complex mean-field \(Z = R e^{i \theta } = 1/N \sum _j e^{i \varphi _j}\) the system can be reduced to

$$\begin{aligned} {\dot{\varphi }}_k = \omega _k + \varepsilon R \sin (\theta - \varphi _k + \alpha _k) \; . \end{aligned}$$
(12)

The order parameter R describes the degree of synchronization, \(R = 1\) denotes full synchrony and \(R = 0\) is an indicator for incoherence or antisymmetry.

One of the most important properties of this model is the analytical solvability. In the case of identical oscillators, the powerful Watanabe-Strogatz (WS) theory can be used [37, 38]. It allows for the reduction of the dynamics from N dimensions to just 3 and \(N-3\) constants of motion. The remaining degrees of freedom are three variables \(\rho \), \(\Psi \) and \(\Theta \). Between them and the mean-field exists a correspondence, although they are not equal. Generally, \(\rho \) and \(\Theta \) are close to R and \(\theta \), while the final variable \(\Psi \) can be seen as a measure of the system’s clustering. The correspondence between the degrees of freedom and the mean-field becomes even bigger in the thermodynamic limit when the dynamics move on the Ott-Antonsen manifold [39, 40] and reduced to just the mean-field variables, R and \(\theta \). The Ott-Antonsen manifold can only be seen as an asymptotic solution, as the transients can be very long [41, 42].

When investigating multiple (M) groups of oscillators, the Kuramoto model can be extended to the M-Kuramoto model. The groups interact with different coupling strength and may have phase shifts,

$$\begin{aligned} {\dot{\varphi }}_k^{\sigma } = \omega _k^{\sigma } + \sum _{\sigma ' = 1}^M \frac{\varepsilon _{\sigma , \sigma '}}{N} \sum _{j = 1}^{N_{\sigma '}} \sin (\varphi _j^{\sigma '} - \varphi _k^{\sigma } + \alpha _{\sigma , \sigma '}) \; .\nonumber \\ \end{aligned}$$
(13)

Here \(\sigma \) and \(\sigma '\) denote the different groups and \(\varepsilon _{\sigma , \sigma '}\) and \(\alpha _{\sigma , \sigma '}\) are the coupling strengths and phase shifts between groups \(\sigma \) and \(\sigma '\), respectively.

Fig. 2
figure 2

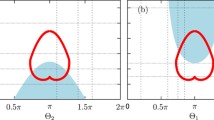
The solitary state in an M-Kuramoto model is visualized in (a). The red ring shows the attractive cluster, the big blue circle the repulsive cluster and the small blue circle the solitary oscillator. In (b) the existence of the solitary state is plotted. The dashed black line shows the analytical prediction for \(N_a = N_r = 5\) and the light gray area the numerical observation. The solid black line and dark gray area show the same, but for \(N_a = N_r =8\)

Full size image

Consider the system with \({\varepsilon _{\sigma , \sigma '} = \varepsilon _{\sigma '}}\) and \({\alpha _{\sigma , \sigma '} = \alpha _{\sigma '}}\) and two groups of identical oscillators, one attractive \(\varphi ^a\) and one repulsive \(\varphi ^r\)

$$\begin{aligned} {\dot{\varphi }}_k^a= & {} \omega _a + \frac{1}{N} \sum _{j = 1}^{N_a} \sin (\varphi _j^a - \varphi _k^a + \alpha _a) \nonumber \\&- \frac{1 + \varepsilon }{N} \sum _{j = 1}^{N_r} \sin (\varphi _j^r - \varphi _k^a + \alpha _r) \nonumber \\ {\dot{\varphi }}_k^r= & {} \omega _r + \frac{1}{N} \sum _{j = 1}^{N_a} \sin (\varphi _j^a - \varphi _k^r + \alpha _a)\nonumber \\&- \frac{1 + \varepsilon }{N} \sum _{j = 1}^{N_r} \sin (\varphi _j^r - \varphi _k^r + \alpha _r) \; , \end{aligned}$$
(14)

where the time was rescaled such that the attractive group has coupling strength 1 and the repulsive \({-(1 + \varepsilon )}\). Then \(\varepsilon \) no longer measures the coupling strength, but the excess of repulsive coupling. These equations can be reduced further by introducing the mean-fields of the groups \({Z_{a, r} = 1/N_{a,r} \sum e^{i \varphi _{a,r}}}\), as before, and a common forcing

$$\begin{aligned} H = \frac{N_a}{N} e^{i \alpha _a} Z_a - \frac{N_r}{N} (1 + \varepsilon ) e^{i \alpha _r} Z_r \; . \end{aligned}$$
(15)

The reduced equations are

$$\begin{aligned} \begin{aligned} {\dot{\varphi }}_a&= \omega _a + {\mathrm{Im}}\left[ H e^{-i \varphi _a}\right] \\ {\dot{\varphi }}_r&= \omega _r + {\mathrm{Im}}\left[ H e^{-i \varphi _r}\right] \end{aligned}, \end{aligned}$$
(16)

and allow for the application of the WS theory to the system [43].

In the system without natural frequencies \({\omega _k^{\sigma } = 0}\) there exists a peculiar solitary state [6], see Fig. 2a. When both groups have the same size \({N_a = N_r}\), the attractive group, and all the repulsive oscillators, except for one, will cluster at the same point. The remaining repulsive oscillator will be phase-shifted by \(\pi \). In the case of \({\alpha _{\sigma '} = 0}\), the state exists for all values of N in some region of \(\varepsilon \) (which shrinks for increasing N), but it does not have full measure, i.e., some initial conditions may lead to a different state. For \({\alpha _{\sigma '} \ne 0}\), the state only exists up to a critical system size and without full measure. The state’s existence is also predicted by the WS theory and is the only allowed clustered state, except for full synchrony.

Since the solitary state is a rather new discovery, there are slightly different definitions of it. The most popular one is that in a system with a natural order of the oscillators, e.g., ordered by their natural frequency, some single oscillators behave differently than the rest of the population and, more importantly, than their immediate neighbors. This is the main difference to a chimera state, where a whole subpopulation exhibits a different behavior. Kapitaniak et al. observed such a state in Ref. [44] with metronomes coupled in a ring to their nearest neighbor and second nearest neighbor. In such a configuration, some single oscillators’ phases will differ from the rest of their synchronized neighbors. Another observation was made in Ref. [45], where superconducting quantum interference devices were placed in a one-dimensional array and coupled magnetically. In this case, the solitary oscillators exhibit a higher amplitude than the rest of the population.

The solitary state has also been found numerically in simulations of coupled Lorenz oscillators [46] and in a ring of coupled Stuart-Landau oscillators with symmetry breaking attractive and repulsive long-range coupling [47]. The observation of the existence in multiplex networks of FitzHugh-Nagumo oscillators coupled in rings with a small mismatch in the intra-layer couplings [48], allows even for controlling strategies to tune the dynamics in, e.g., neural networks.

While the existence has been shown in many different systems, there are only a few results in investigating its emergence and stability. In a Kuramoto model with inertia, the solitary state arises from a homoclinic bifurcation and persists even in the thermodynamic limit [49], in contrast to it being a finite size effect in the M-Kuramoto model with attractive and repulsive interaction. Aside from differential equations, the solitary state has also been found in coupled maps. Multiplex network of non-locally coupled maps with a singular hyperbolic attractor exhibit solitary states in their transition from coherence to incoherence [50, 51]. During the transition, more and more solitary oscillators appear, growing almost linearly with the decrease in the coupling strength. This is the result of an increase of the size of the basin of attraction of the solitary set with a decrease in the coupling, as more random initial conditions lie in this basin [52]. To also induce solitary states in maps with nonhyperbolic attractors, a multiplicative noise can be added to the coupling constant, thus also showing the existence of the solitary state in a noisy system [53].

These solitary state can consist of multiple solitary oscillators, but from here on, a solitary state is defined more narrowly, such that a single oscillator shows a different behavior than the rest of the population.

In Ref. [17] we extend the M-Kuramoto model from Ref. [6] to consider non-identical groups without phase shift \({\alpha _a = \alpha _r = 0}\). The oscillators in each group are identical, but there exists a difference in the natural frequencies \(\omega \), i.e., in Eqs. (14) \({\omega _a = 0}\) and \({\omega _r = \omega }\). In this case the solitary state changes: the cluster of the repulsive oscillator has a small phase-shift in relation to the cluster of the attractive oscillators and the phase-shift between the repulsive cluster (or the attractive cluster) and the solitary oscillator is no longer \(\pi \). The solitary state also has full measure, it will always be reached, regardless of the initial condition. The region of existence of the solitary state, as well as the phase shifts between the clusters and the solitary oscillator can be calculated and fits well to numerical observations, see Fig. 2b. The state is also not stationary, but rotates with a constant frequency

$$\begin{aligned} \nu = \frac{1 + \varepsilon }{\varepsilon } \omega \; . \end{aligned}$$
(17)
Fig. 3
figure 3

Parameter space of the M-Kuramoto model in Eqs. (14) with non-identical groups. The color shows the average order parameter of the repulsive group \({\bar{R}}_r\). Full synchrony is denoted by the black region, the solitary state by the red region and the white lines show the condition of existence for the fully synchronous state

Full size image

Aside from the solitary, there exist two other states in the system (Fig. 3), a fully synchronous state and a self-consistent partial synchronous state. In the fully synchronous state both clusters are fully synchronized, have a constant phase shift, and rotate with a uniform frequency. The region of existence and the stability of the state can be calculated directly from Eqs. (14). The results show that the region of stability with

$$\begin{aligned} \omega = \pm \sqrt{- \frac{\varepsilon ^3}{2} - \frac{\varepsilon ^4}{4}}, \end{aligned}$$
(18)

is slightly smaller than the region of existence, which fits the numerical results in Fig. 3. The frequency has the same relation as the solitary state in Eq. (17). We also find numerically that the attractive group always fully synchronizes, even outside the fully synchronous state, although there is no analytical proof for this. A simple check of the stability for the attractive cluster yields the inequality

$$\begin{aligned} R_r \cos (\theta _r - \theta _a) < (1 + \varepsilon )^{-1} \; . \end{aligned}$$
(19)

The exact dynamics of the mean-field quantities are unknown, so this cannot be solved analytically, but simulations show that \({\theta _r - \theta _a}\) is quite small and \(R_r\) falls off very quickly with \(\varepsilon \) so that this equality is always fulfilled, and the attractive group fully synchronizes.

Fig. 4
figure 4

Goodness of fit for the WS theory in the M-Kuramoto model from Eq. (14). In (a) the difference between the numerical (\({\bar{\nu }}_{n, r}\)) and analytical (\({\bar{\nu }}_{a, r}\)) average frequency for the single oscillators (dashed black line) and the mean-field (solid black line, \(\bar{{\dot{\theta }}}_{r}\)) of the repulsive group is shown. The frequencies were averaged over 100 different initial conditions for \(N_a = N_r = 5\) and \(\varepsilon = 0.5\). In (b) the average order parameter is plotted, where the blue crosses (black dots) show different initial conditions for \(\omega = 0.02\) (\(\omega = 0.6\)) and their analytical value as a solid black line (green dashed line)

Full size image

The final state, self-consistent partial synchrony, is defined by the difference in average frequencies between the single oscillators and their mean-field [54]. The oscillators of the repulsive group move at a frequency that is generally faster than their mean-field. The WS theory cannot be applied to the whole system at once to explain this behavior, but on each group separately [43]. Making the crude approximation of the thermodynamic limit as well as stationarity (numerically we find that the average frequencies of both mean-fields coincide), allows for the calculation of the mean-field variables on the Ott-Antonsen manifold. As expected, they do not fit well for small \(\omega \) or \(\varepsilon \), but give a surprisingly good approximation for big \(\omega \) and \(\varepsilon \), even for a small system of \({N_a = N_r = 5}\), see Fig. 4. With the now known average values of \(R_r\) and \({\dot{\theta }}_r\) it is possible to calculate the average frequency of the oscillators in the WS theory [55] as (bars denote the time-average)

$$\begin{aligned} {\bar{\nu }}_r = \frac{1 - {\bar{R}}_r^2}{1 + {\bar{R}}_r^2} \omega + \frac{2 {\bar{R}}_r^2}{1 + {\bar{R}}_r^2} \bar{{\dot{\theta }}}_r \; , \end{aligned}$$
(20)

which shows clearly the expected difference between the average frequency of the mean-field and the single oscillators.

Even in a simple model of phase coupled oscillators in the weak coupling limit, it is possible to find interesting dynamical states. This can be extended further by considering more complex coupling schemes than simple all-to-all coupling. For even richer dynamics, higher-order coupling terms need to be considered.

3.2 Higher order phase dynamics—Stuart-Landau model

Extending the first order phase approximation for coupled oscillators in Eq. (10) to higher orders needs knowledge of the phase dynamics of the uncoupled units. One of the oscillators with a known analytical phase is the Stuart-Landau oscillator [2, 56]. Its dimensionless dynamics in a coupled system are

$$\begin{aligned} \frac{d A}{dt}= & {} (1 + i \omega ) A - \left| {A} \right| ^2 A - i \gamma A(\left| {A} \right| ^2 - 1)\nonumber \\&+ \varepsilon G(A_1, A_2, \ldots ) \; , \end{aligned}$$
(21)

where A is a complex amplitude, \(\omega \) is the frequency and \(\gamma \) is the non-isochronicity parameter and determines \(\Phi (A)\). Using \({A = R e^{i \theta }}\) leads to

$$\begin{aligned} \begin{aligned} {\dot{R}}&= R - R^3 + \varepsilon {\mathrm{Re}}\left[ e^{-i \theta } G\right] \\ {\dot{\theta }}&= \omega - \gamma (R^2 - 1) + \varepsilon R^{-1} {\mathrm{Im}}\left[ e^{-i \theta } G\right] \; . \end{aligned} \end{aligned}$$
(22)

From there it follows for the phase of the uncoupled system \({\varphi = \theta - \gamma \ln (R)}\) and

$$\begin{aligned} \begin{aligned} {\dot{R}}&=\, R - R^3 + \varepsilon {\mathrm{Re}}\left[ e^{-i (\varphi + \gamma \ln R)} G\right] \\ {\dot{\varphi }}&=\, \omega + \varepsilon R^{-1} \left( {\mathrm{Im}}\left[ e^{-i (\varphi + \gamma \ln R)} G\right] \right. \\&\qquad \left. - \gamma {\mathrm{Re}}\left[ e^{-i (\varphi + \gamma \ln R)} G\right] \right) \; . \end{aligned} \end{aligned}$$
(23)

In Ref. [15], eight nanomechanical systems (NEMS) with dynamical equations resembling the Stuart-Landau oscillator were coupled in a circle. The oscillators were connected with their two neighbors, and the coupling term consisted of the average of them. The resulting phase reduction up to the second order in the coupling strength contained terms not present as physical links in the coupling scheme, such as \({\sin (\varphi _{k+2} - \varphi _k)}\), \({\sin (\varphi _{k+2} - 2 \varphi _{k+1} + \varphi _{k})}\) and similar terms in the opposite direction. These non-structural terms only appear in the second-order approximation and would not be recovered in the typical first-order phase reduction. The observed system exhibits many dynamical states, such as traveling waves or weak chimeras, which would not necessarily be expected in the first-order phase approximation. Numerical simulations of the phase model show good agreement with the experimental results, pointing to the importance of the non-structural coupling terms in complex synchronization behavior.

Similarly, in Ref. [14] a system of coupled Stuart-Landau oscillators was investigated numerically. The oscillators were coupled all-to-all to their mean-field. In the phase reduction up to the second-order in \(\varepsilon \) appeared terms of the form \({\sin (\varphi _m + \varphi _n - 2\varphi _k)}\), where m, n and k are all possible combinations, coupling three oscillators. They determined that these terms are necessary to explain the system’s full dynamics but are again not present in the first-order phase dynamics, which only contains the existing pairwise connections.

In both Refs. [14, 15] with coupled Stuart-Landau-like oscillators, the first-order approximation of the phase dynamics yields a Kuramoto-like model. This allows the novel terms to be seen as an extension of the Kuramoto model in Eq. (11) to higher coupling strength.

Fig. 5
figure 5

A system of three Stuart-Landau oscillators coupled in a line. The \(A_k\) denote the complex amplitudes and the \(c_{j,k}\) the coupling terms between the oscillators

Full size image

Based on the observations for the NEMS we investigated the higher order phase reduction for a system of three coupled nonidentical Stuart-Landau oscillators in Ref. [18]. In difference to Ref. [14] one pairwise connection is missing. The coupling scheme is a line, as can be seen in Fig. 5 and is given by

$$\begin{aligned} G_k(A_k, A_{k-1}, A_{k+1})= & {} c_{k-1, k} e^{i\beta _{k-1, k}} A_{k-1}\nonumber \\&+ c_{k+1, k} e^{i\beta _{k+1, k}} A_{k+1} \; , \end{aligned}$$
(24)

where the \(c_{j, k}\) are of \({{\mathcal {O}}(1)}\) and the \(\beta _{j, k}\) are phase shifts between the two oscillators. To extend the phase reduction beyond the first order in \(\varepsilon \) we use a perturbation method, where the R and \({\dot{\varphi }}\) are functions of the phases and expand them as a power series

$$\begin{aligned} \begin{aligned} R&= 1 + \varepsilon r^{(1)}(\varphi , \varphi _1, \varphi _2, \ldots ) + \varepsilon ^2 r^{(2)}(\varphi , \varphi _1, \varphi _2, \ldots ) + \cdots \\ {\dot{\varphi }}&= \omega + \varepsilon \psi ^{(1)}(\varphi , \varphi _1, \varphi _2, \ldots ) + \varepsilon ^2 \psi ^{(2)}(\varphi , \varphi _1, \varphi _2, \ldots ) + \cdots \; . \end{aligned} \nonumber \\ \end{aligned}$$
(25)

In the dimensionless form the limit cycle of the uncoupled oscillator has the amplitude \({R_0 = 1}\), as can be easily checked in Eq. (22). Inserting these assumptions in Eq. (23), the dynamics of \(r^{(1)}\), \(r^{(2)}\), \(\psi ^{(1)}\), \(\psi ^{(2)}\) and so on can be found by gathering the powers of \(\varepsilon \). The full calculation is rather long, so please see Ref. [18] for a detailed explanation. Here it will suffice to say that to find the phase dynamics in the second order in \(\varepsilon \), a partial differential equation has to be solved using a Fourier series to represent the coupling function \(G_k\). This representation is motivated by the fact that \(G_k\) has to be \(2\pi \)-periodic for all the phases. The resulting reduction for the first oscillator up to the second order in \(\varepsilon \) is

$$\begin{aligned} {\dot{\varphi }}_1= & {} \omega _1 + \varepsilon c_{2,1} [\sin (\varphi _2 - \varphi _1 + \beta _{2,1}) - \gamma \cos (\varphi _2 - \varphi _1 + \beta _{2,1})] \nonumber \\&+ \varepsilon ^2 \left[ a_{1; 0,0,0}^{(2)} + a_{1; -2,2,0}^{(2)}\cos (2\varphi _2 - 2\varphi _1)\right. \nonumber \\&\left. + b_{1; -2,2,0}^{(2)}\sin (2\varphi _2 - 2\varphi _1) \right. \nonumber \\&+ a_{1; -1,2,-1}^{(2)}\cos (2\varphi _2 - \varphi _1 -\varphi _3)\nonumber \\&+ b_{1; -1,2,-1}^{(2)}\sin (2\varphi _2 - \varphi _1 - \varphi _3) \nonumber \\&\left. + a_{1; -1,0,1}^{(2)}\cos (\varphi _3 - \varphi _1) + b_{1; -1,0,1}^{(2)}\sin (\varphi _3 - \varphi _1)\right] \; ,\nonumber \\ \end{aligned}$$
(26)

with \(a_{k; \varvec{l}}^{(j)}\) and \(b_{k; \varvec{l}}^{(j)}\) denoting the coefficients for cosine and sine terms respectively and k being the index of the oscillator. A vector of integers \(\varvec{l}\) contains the coefficients before the phases and j the power in \(\varepsilon \).

Using the perturbation method up to the second order in \(\varepsilon \) yields again non-structural terms in Eq. (26), e.g. terms of the form \({\sin (\varphi _3 - \varphi _1)}\). Aside from these, there exist additional terms coupling all three oscillators \({\sin (2\varphi _2 - \varphi _1 -\varphi _3)}\) and second harmonics \({\sin (2\varphi _2 - 2\varphi _1)}\). The coefficients of the second order also contain the frequency difference between the oscillators, whereas the first order terms do not.

A Fourier Ansatz is used to measure the coupling terms numerically and verify the analytical results. The phase dynamics are \({2\pi }\)-periodic, so they can be written as a multidimensional Fourier series

$$\begin{aligned} {\dot{\varphi }}_k = a_{k; \varvec{0}} + \sum _{\varvec{l} \ne 0} \left[ a_{k; \varvec{l}} \cos (\varvec{\varphi } \cdot \varvec{l}) + b_{k; \varvec{l}} \sin (\varvec{\varphi } \cdot \varvec{l}) \right] \; , \nonumber \\ \end{aligned}$$
(27)

where \({\varvec{\varphi } = (\varphi _1, \varphi _2, \ldots , \varphi _N)}\) is a vector of all the phases, \(\varvec{l}\) an N-dimensional vector of integers and \({\varvec{\varphi } \cdot \varvec{l} = \sum _j \varphi _j l_j}\) the scalar product. The \(a_{k, \varvec{l}}\) and \(b_{k, \varvec{l}}\) are Fourier coefficients. This form resembles the analytical results in Eq. (26) and finding the relevant coupling terms is reduced to fitting the Fourier coefficients \(a_{k; \varvec{l}}\) and \(b_{k; \varvec{l}}\) up to some maximum value with \({\left| {l_j} \right| \le m}\). Because the coupling function is real, \({a_{k;-\varvec{l}} = - a_{k; \varvec{l}}}\) and the number of coefficients to consider halves. Still, the number of terms that need to be fitted scales like \(m^3\), which increases the necessary number of data points for a good fit very rapidly with m and leads to the curse of dimensionality.

In the case of partial synchrony, the Fourier coefficients can be fitted onto one long time series, although some initial transient has to be integrated over before the dynamics reach the torus spanned by the phases. For a good fit, the trajectory should be long enough to cover the whole torus. However, this is not the case in the synchronous regime; instead, the dynamics will settle on a single synchronized trajectory. The integration has to be stopped before reaching this synchronous trajectory and restarted with different initial conditions until the torus is sufficiently filled.

Fig. 6
figure 6

Comparison of analytical and numerically fitted modes for the Stuart-Landau oscillators with coupling function Eq. (24) in the partial synchronous regime. The modes shown are the cosine terms for the first oscillator in Eq. (26). In (a) and (b) the red circles denote numerically fitted values for terms appearing in Eq. (26), while their analytical values are shown as green boxes. Black triangles denote terms \({\sum _j l_j = 0}\), which are the only allowed terms, because of rotational symmetry. The blue crosses are all other modes up to \({\varvec{l} = (4, 4, 4)}\). In (c) the difference between the analytical and numerically fitted modes are shown. The gray dashed line is a polynomial \(\varepsilon ^3\), so the error scales stronger than \(\varepsilon ^3\)

Full size image

Fitting the coefficients for different coupling strengths \(\varepsilon \) yields the power series

$$\begin{aligned} a_{k; \varvec{l}} = a_{k; \varvec{l}}^{(0)} + \varepsilon a_{k; \varvec{l}}^{(1)} + \varepsilon ^2 a_{k; \varvec{l}}^{(2)} + \cdots , \end{aligned}$$
(28)

and a similar series for \(b_{k; \varvec{l}}\). The coupling function is then reconstructed by comparing these series and Eq. (27). The results of this method fit very well to the analytical prediction, as can be seen in Fig. 6.

The numerical method to reconstruct the phase can also be used in cases where the phase is unknown, but then the phases and their derivatives have to be calculated numerically. For finding the phase, an autonomous copy of each oscillator is integrated. It evolves for a number of its autonomous periods T until it reaches its limit cycle. The phase after the relaxation is then also the phase of the point before the relaxation. To find the derivative, one observes the infinitesimal time step dt of the perturbed system and sets it in relation to a different time step \({\overline{dt}}\) on the limit cycle. This time difference \({\overline{dt}}\) is determined by the motion on the limit cycle and the derivative \(\varvec{f}\) in Eq. (1). Using the relation of dt and \({\overline{dt}}\) allows the calculation of the phase derivative, even if the oscillator is perturbed far from its limit cycle. For a full explanation and the resulting equation, see Ref. [18].

4 Summary

Phase dynamics are an important tool to analyze dynamical systems. In the case of a simple perturbation of an ensemble of oscillators, this reduces, in the first order, to the collective PRC. The PRC has been investigated for a system of coupled Rayleigh oscillators, where it took a long time to fully relax back onto the limit cycle after the perturbation, even in comparison to the time needed for synchronization. This makes the collective PRC only usable as an approximate description in noisy environments, where it is perturbed again before it can fully settle.

In the paradigmatical Kuramoto model with two groups, one attractive and one repulsive, an interesting solitary state is observed that does not appear in a model with just one group. A single solitary oscillator leaves its otherwise fully synchronized group in this state and gets phase-shifted by \(\pi \). The use of groups with different natural frequencies leads to a stabilization of this state.

In the case of phase dynamics for the description of a coupled system, most of the current works use the first-order phase approximation. The first-order reduction for pairwise coupled units yields only pairwise terms in the phase model. When extending the phase reduction beyond the first-order, new connections arise that are necessary to describe more complicated dynamics. Even in a simple model of three Stuart-Landau oscillators, coupled in a line, the second-order approximation consists only of higher-order or non-structural terms. The analytical derivation of the additional terms follows from a simple perturbation Ansatz. A numerical verification shows good agreement and supports the analytical findings.