Chaos in fractional system with extreme events

Abstract

Understanding extreme events attracts scientists due to substantial impacts. In this work, we study the emergence of extreme events in a fractional system derived from a Liénard-type oscillator. The effect of fractional-order derivative on the extreme events has been investigated for both commensurate and incommensurate fractional orders. Especially, such a system displays multistability and coexistence of multiple extreme events.

1 Introduction

The famous Japanese paint The Great Wave off Kanagawa [1] illustrates an example of “extreme event”. The sudden appearance of the large wave threatening fishing boats relates to rogue waves [2, 3]. Extreme events are characterized by extreme observed values or statistical measurements. It is noted that there are numerous definitions of extreme event in different disciplines, however, researchers have attempted to introduce a systems-based definition of extreme event [4, 5]. Extreme events occur in a wide range of fields from nature, economics, society to engineering. Extreme events in nature were often reported as tsunamis, earthquakes, tornadoes, hurricanes, droughts, floods, and so on [6, 7]. Natural extreme events launch natural hazards causing damage on people[8,9,10]. Market crashes, credit risk are examples of extreme events in economics [11]. In engineering, power blackouts, machine failures can be considered as extreme events [12, 13]. The rapid increase of new coronavirus infections in northern Italy in February 2020 can be considered to be an extreme event [14,15,16]. Monitoring and predicting extreme events likes heart attack and epilepsy is the main aim of ubiquitous health-care systems [17, 18]. Extreme event may be a tipping point in changing the global dynamics and inference of extreme event should be discovered further [19].

Kingston et al. introduced a Liénard-type oscillator including forcing $Asin(\omega t)$ [20]. Authors observed extremely large amplitude oscillations in one of the system state variables when changing amplitude and the frequency of the forced signal. Extreme and critical transition events were found in Liénard system with memristor [21]. Extreme events and spatiotemporal chaos were measured in a microcavity laser [22]. In the recent work [23], authors proposed a networks of Josephson junctions and obtained extreme events in a sub-population. Dynamical and statistical characteristics were studied indicating routes to extreme events [24]. Although extreme event has been an attractive object of various researches on integer order systems, there are few studies investigated extreme events in fractional order systems. Investigating extreme events in fractional order systems contributes to a deeper understanding of extreme events.

A fractional-order system is studied in this work. Model and dynamics of system are reported in Sect. 2. Especially we focus on extreme events of the system in Sect. 3. The last section concludes our work.

2 Fractional oscillator

Let be start with some basic definitions of fractional calculus [25]:

Definition 1

The Riemann–Liouville fractional integral of order $q>0$ of $f \in [C,T]$, $T>0$ is defined as

$$\begin{aligned} I^qf(t)=\frac{1}{\varGamma (q)}\int ^t_0\frac{f(\tau )}{(t-\tau )^{(1-q)}}d\tau . \end{aligned}$$

(1)

Definition 2

The Caputo derivative of order $q\in [k-1,k]$, $K\in N$ of $f\in C^k(0,T]$, $T>0$ is defined as

$$\begin{aligned} D^qf(t)= \left\{ \begin{array}{l} \frac{1}{\varGamma (k-q)}\int ^t_0 (t-\tau )^{k-q-1}f^{(k)}(\tau )d\tau , \quad q\in (k-1,k), \\ f^{(k)}(t), q=k. \end{array} \right. \end{aligned}$$

(2)

We consider fractional-order oscillator (3):

$$\begin{aligned} \begin{array}{l} D^{q_1}x = y, \\ D^{q_2}y = -axy + bx - cx^3 + dsin(\omega t), \end{array} \end{aligned}$$

(3)

where a is the nonlinear damping, c is the strength of nonlinearity, and b relates to the internal frequency of the system. Parameters d and $\omega$ are amplitude and forcing frequency of the external sinusoidal signal. Here $D^{q}$ is q-order Caputo differential operator [25,26,27], $0<q_{i}\le 1$ $(i=1,2)$ are the derivative orders of the state variables x, y. Oscillator (3) is a Liénard-type oscillator. Liénard-type oscillator is attractive because it is simple but displays multistability. In addition, Liénard-type oscillator presents a wide class of systems which have broad applications [20]. The fractional-order system (3) is called as commensurate if $q_1=q_2$ and incommensurate otherwise. In this work, the Adams–Bashforth–Moulton predictor–corrector method [28, 29] is used for the numerical simulations.

System (3) has three equilibria: $E_1(0,0), E_2(-1,0)$ and $E_3(1,0)$. The Jacobian matrix of fractional-order system (3) is given by

$$\begin{aligned} J= \left[ \begin{array}{cccc} 0 &{}&{} 1 \\ -ay+b-3cx^2 &{}&{} -ax. \\ \end{array} \right] \end{aligned}$$

To study the stability of commensurate order system (3) for parameters $a=0.45, b=0.5,c=0.5,d=0.2$, and forcing frequency $\omega =0.7315$, the eigenvalues $\lambda _i$, $i=1,2$ of the Jacobian matrix J are evaluated at each equilibrium point $E_i$ and mentioned in Table 1.

Theorem 1

If the eigenvalues for the equilibria $E_i,$ $i=1,2,3$ of the Jacobian matrix J satisfy the following condition:

$$\begin{aligned} arg\left( \lambda _i \right) > q\pi /2, \quad 0<q<1. \end{aligned}$$

The fractional-order forced system (3) is asymptotically stable, where the derivative orders $q_1=q_2=q.$

Table 1 Eigenvalues and equilibria of system (3)

For the equilibrium $E_2$, it is obtained

$$\begin{aligned} arg(0.2250+0.9744i)\times 2/{\pi } \approx 0.86 \end{aligned}$$

that means from Theorem 1, the commensurate order system (3) is stable for $q<0.86$ and we can conclude that fractional system (3) exhibits chaotic dynamics when $q>0.86$ for $E_2$.

Fig. 1

a Bifurcation diagram, b Lyapunov exponents, c Phase portraits of commensurate order system (3) for $q\in (0.98,1), a=0.45, b=0.50,c=0.50,d=0.20, \omega =0.7315$, and initial conditions $(x_0,y_0)=(1,-0.5)$

To verify this result numerically, the bifurcation diagram, Lyapunov exponents and phase portraits are plotted in Fig. 1 for $q\in (0.98,1)$ and initial conditions $(x_0,y_0)=(1,-0.5)$. From the bifurcation diagram, we can see that the commensurate order system (3) does not remain chaotic behavior for $q<0.988$. When $0.988\le q<0.997$ the system (3) displays transition from periodic to chaotic states. route to chaos. The system exhibits complex chaotic attractor over most of the range $q\in (0.997,1)$. The existence of a positive Lyapunov exponent confirms that the fractional-order system shows chaotic behavior. From the plot of Lyapunov exponents we observe that the fractional system (3) is chaotic for $q>0.997$. The phase portraits in the $x-y$ plane illustrate the periodic orbits with different periods for $q=0.98$, $q=0.99$, $q=0.996$ and complex chaotic attractor for $q=0.999$.

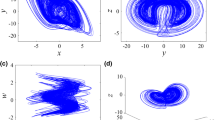
The choice of initial conditions is related with the basin of attraction of fractional-order system (3) which is shown in Fig. 2 for the commensurate order $q=0.996$. Like the integer case (see [20]), the fractional-order system (3) has two basin of attractions: BAC and BAD these mean the basin of attraction of the conservative and dissipative system, respectively, HO (blue line in Fig. 2) means the homoclinic orbit which is located inside the BAD. Figure 3 shows different dynamics of fractional system (3) for different sets of initial conditions from the region of BAD. When we choose initial conditions in the region inside the homoclinic orbit, the system (3) exhibits a bounded chaotic attractor for $\omega =0.7315$ and $q=0.999$, as well as a chaotic attractor with occasional large amplitude oscillations for $\omega =0.65$ and $q=0.993$. When we choose other initial conditions outside the homoclinic orbit, the system exhibits a quasiperiodic trajectories for $\omega =0.65$, and $q=0.993$. So, for $q=0.993$, $\omega =0.65$ and with two choices of initial conditions: inside and outside the HO; the fractional forced Liénard system (3) can exhibit a coexistence of chaotic attractor with large trajectories and quasiperiodic attractor which are shown in Fig. 4 (red and green trajectories respectively). As a notice here, the orbits of chaotic attractor are always limited by the coexisting quasiperiodic trajectories.

From the previous results, it can be remarked that the system exhibits a bounded attractor but under some values of system parameters, we noticed that the appearance of large amplitude oscillations from the bounded chaotic motion. These large oscillations are vital signatures of the existence of extreme events in the fractional-order system (3) which will be discussed further in the next section.

Fig. 2

Two basin of attractions of fractional-order system (3) for $q=0.996$: the BAC outer the red orbit and the BAD inside the red orbit with the HO in blue line. The equilibrium points in dashed spiral; $E_1$ at (0, 0); $E_2$ (green arrows) at $(-1,0)$, $E_3$ (black arrows) at (1, 0)

Fig. 3

a Bounded chaotic attractor for $\omega =0.7315,q=0.999$ and $(x_0,y_0)=(1,-0.5)$, b chaotic attractor with large trajectory for $\omega =0.65,q=0.993$ and $(x_0,y_0)=(1,-0.5)$, c quasiperiodic trajectories for $\omega =0.65,q=0.993$ and $(x_0,y_0)=(1.5,1.93)$

Fig. 4

Trajectories of the commensurate order system (3) for $q=0.9930$,$\omega =0.65$ and two choice of initial conditions; coexisting of chaotic attractor with large trajectories in red color at $(x_0,y_0)=(1,-0.5)$(inside the HO) and quasiperiodic attractor in green color at $(x_0,y_0)=(1.5,1.93)$ (outside the HO)

Fig. 5

a Bifurcation diagram, b Lyapunov exponents and c phase portraits of commensurate order system (3) for $a = 0.45, c = 0.50, b = 0.50, d = 0.20, \omega = 0.65$ at $(x_0,y_0) = (1,-0.5)$ with varying $q\in (0.992,1)$

Fig. 6

Time series of commensurate order system (3) for $a = 0.45, c = 0.50, b = 0.50, d = 0.20, w = 0.65$ at $(x_0,y_0) = (1,-0.5)$ with varying q. a Bounded chaos for $q= 0.9929$, b extreme event for $q = 0.9930$, c multiple large amplitude events for $q = 0.9960$. The horizontal red lines indicate the threshold $H_S$

Fig. 7

Coexisting of chaotic attractor and extreme events in red lines at $(x_0,y_0)=(1,-0.5)$ (inside the HO) with the quasiperiodic attractors in green lines at $(x_0,y_0)=(1.5,1.93)$ (outside the HO) in 3D-spaces; a bounded chaos for $q= 0.9929$, b extreme event for $q = 0.9930$, c multiple large amplitude events for $q = 0.9960$

Fig. 8

a Bifurcation diagram, b Lyapunov exponents and c phase portraits of incommensurate order system (3) for $\omega = 0.68$, $q_2 = 1,$ while varying $q_1$

3 Extreme events in fractional oscillator

In this section, we discuss the effect of fractional-order derivative on the extreme events in system (3) by varying parameters of the commensurate and incommensurate fractional-order systems. Bifurcation diagrams, Lyapunov exponents, extreme event qualifier $H_s$, and numerical probability distribution function (PDF) are used to distinguish different cases of the system dynamics: bounded chaos, extreme events via intermittency route, extreme events via an interior crisis, and coexistence of multiple large-amplitude oscillations.

3.1 Extreme events with respect to commensurate order q

Let set $a=0.45, c=0.50,b=0.50,d=0.20,$ the frequency $\omega =0.65$ and the initial conditions here are chosen inside the HO. We analyze system (3) by varying the commensurate order q. The bifurcation diagram and Lyapunov exponents for this case is plotted in Fig. 5. By observing the bifurcation diagram, it can be seen when $q<0.993$, the system (3) exhibits a periodic oscillation but when $q=0.993$ (arrow L), sudden changes occur in the amplitude of the oscillation which bifurcates to chaotic trajectory with large size. When $0.9933\le q<0.9555$, the system comes back to display periodic oscillation in small ranges at this domain and then bifurcates again to chaos with large size. These large chaotic trajectories continue to appear with increasing commensurate order q from 0.9955 to 1. The same results about the existence of chaos are found from the plot of Lyapunov exponents that presents the transition between positive values and negative values when $0.993\le q<0.9955$. Positive values continue to exist when $q>0.9955$. From Fig. 5c, it can be seen different phase portraits of fractional system (3) for different values of fractional order q. The system exhibits periodic orbits or chaotic attractor with large size when $0.9933\le q<0.9555$ which confirms the previous results. Also, a chaotic attractor with large size is shown for $q=0.9970$. Therefore, the fractional-order system (3) exhibits a periodic orbit that bifurcates to chaos with sudden expansion in the trajectories at the critical point L ($q=0.9930$) through an intermittency route. The emergence of sudden expansion near critical fractional order is a signature of extreme events. To characterize this sudden expansion as an extreme event, we estimate numerically the extreme event qualifier, $H_S$. For the estimation of $H_S$, we take the following steps:

• Calculate the y(t) state variable by taking long temporal data as possible.

• Measure the peak values y(t), i.e. $P_n$.

• Estimate the mean of the peaks $<P_n>$ and standard deviation $\sigma$.

• Calculate the threshold $H_s$: $H_s=<p_n>+8\sigma$.

• Plot the time series of y(t) as function of t in short runs for better visualization and replot the $H_s$ lines.

Especially, if the large-amplitude peaks of the state variable of the system exceed $H_s$ they can be defined as extreme events. The time series of commensurate order system (3) is plotted in Fig. 6 for three cases. A bounded chaos is shown in Fig. 6a for $q = 0.9929$ (arrow C in Fig. 5). Extreme events is shown in Fig. 6b for $q = 0.9930$ (arrow L in Fig. 5) near the intermittency regime. Here, the large excursions of the amplitude of y(t) fluctuates intermittently between two phases: laminar phase which always remains bounded and turbulent phase. In the turbulent phase, the system exhibits large amplitude oscillations which is also exceed the threshold $H_s$ (red line in Fig. 6b). Figure 6c shows the third case for $q = 0.9960$ (a value between $q=0.9955$ and $q=1$ in Fig. 5). This case does not qualify as an extreme event because the system exhibits multiple large events with a high average value and, therefore, the threshold $H_s$ becomes larger above the largest peaks.

The fractional-order system (3) can be presented also into 3D-space spanned by x, y, and t. Coexisting attractors of the system (3) are plotted in Fig. 7 on 3D-space for two initial conditions inside and outside the HO (see Fig. 4); quasiperiodic attractor in green line and chaotic attractor in red line. The 3D chaotic trajectories of system (3) are shown in Fig. 7a–c that match to their time series in Fig. 6a–c, respectively. The plots show the different dynamics of the system for different commensurate order values: a bounded chaos for $q=0.9929$ in Fig. 7a, extreme events for $q=0.9930$ in Fig. 7b and multiple large amplitude events for $q=0.9960$ in Fig. 7c. It can be remarked in Fig. 7 that the red trajectories stay always inside the green trajectories for all the three cases and this confirms the results obtained in Sect. 2 concerning that chaotic and extreme events are confined within the boundaries of quasiperiodic attractor.

Fig. 9

Time series of incommensurate order system (3) for $\omega = 0.68$, $q_2 = 1,$ and varying $q_1$: a $q_1=0.9770$, b $q_1=0.9780$, c $q_1=0.9850$

Fig. 10

a Bifurcation diagram, b Lyapunov exponents and c phase portraits of incommensurate order system (3) for $\omega = 0.68$, $q_1 = 1,$ while varying $q_2$

Fig. 11

Time series of incommensurate order system (3) for $\omega = 0.68$, $q_1 = 1,$ and varying $q_2$: a $q_2=0.9774$, b $q_2=0.9775$, c $q_2=0.9850$

3.2 Extreme events with respect to incommensurate orders $q_1,q_2$

In this subsection, we assume the incommensurate order $q_1\ne q_2$ and we study if the change of the fractional-order from commensurate case to the incommensurate case has an effect or not on the dynamics of extreme events.

Let set $a=0.45,c=0.50,b=0.20,\omega =0.68$ and the incommensurate orders are chosen as varying $q_1\in (0.96, 1),q_2=1$ and varying $q_2\in (0.96, 1),q_1=1$. Bifurcation diagrams, Lyapunov exponents, phase portraits and time series are plotted in Figs. 8, 9, 11 and 11 for initial conditions $(x_0,y_0) = (1,-0.5)$ inside the HO. As can be seen from the bifurcation diagrams, when the fractional-orders $q_1,q_2$ increase from 0.965 to 1, the system exhibits a period-doubling route to chaos with small amplitude but a very small change at the values of orders from arrow C to arrow L occurs suddenly a transition from small to very large amplitude chaotic oscillations through interior crisis. The expanded attractor continues to appear for $q_1\in (0.97780,1)$ (see Fig. 8a), $q_2\in (0.9775,1)$ (see Fig. 10a). The existence of chaotic behavior in the system is observed also in the plot of Lyapunov exponents in the same interval as above. The periodic orbits, bounded chaotic attractors and chaotic trajectories with large size are shown in Figs. 8c and 10c for different values of incommensurate orders $q_1$ and $q_2$ Here, an other scenario of extreme events is found which is extreme events via an interior crisis. From the plot of time series, we can see the different cases of extreme events which are mentioned in Table 2. When $q_1=0.9780,q_2=1$ and $q_2=0.9775,q_1=1$ (arrow L in bifurcation diagrams), the system occurs randomly chaotic oscillations with large peaks exceed the threshold $H_s$, these large events distinguish as an extreme events.

Table 2 Three considered dynamic cases

Now, we discuss the statistical properties of the dynamics during this scenario, leading to the emergence of extreme events. When $q_1=0.9780,q_2=1$ and $q_2=0.9775,q_1=1$, the numerical PDFs (probability distribution function of all the peaks $p_n$) are estimated for both the time series in Figs. 9b and 11b. For the estimation, we take a long time series as possible of state y(t), measure the peaks $P_n$ then the PDFs have constructed and plotted in Fig. a–b. The vertical dashed lines in the figures indicate the threshold $H_s$. As a remark here, the saturation in the $H_s$ is related to the length of temporal data. It can be seen from the figures long-tailed distributions overriding the threshold $H_S$. These results affirm the existence of extreme events. Figure c is a combination of the previous PDFs to compare between the extreme events. This combination shows that the distributions of varying $q_1$ have a long-tailed than the distributions of varying $q_2$.

Fig. 12

Numerical PDF of $P_n$ for different incommensurate order values for a $[q_1,q_2] = [0.9780,1]$, b $[q_1,q_2] = [1,0.9775]$, c combination of sub-figures (a) and (b). Vertical dashed lines present the thresholds $H_s$

Fig. 13

Bifurcation diagram for commensurate order $q=0.996$ and varying $\omega \in (0.63,0.8)$

As a result, the type of fractional order such as commensurate or incommensurate has an effect on the processes of occurrence of extreme events. From Sect. 3.1, it can be remarked that the oscillation fluctuated intermittently between laminar phase and turbulent phase. So, the commensurate order system exhibits these events via an intermittency route but in Sect. 3.2, the the oscillation appeared randomly. So, the incommensurate order system exhibits these events via an interior crisis.

Fig. 14

Time series and numerical PDF of $P_n$ with commensurate order $q=0.996$ for (a, b $\omega =0.647$ (arrow L in Fig. 13) and c, d $\omega =0.7055$ (arrow R in Fig. 13). The red line indicates threshold $H_s$

Fig. 15

a Bifurcation diagram and time series for commensurate order $q=0.996,\omega =0.65$ and varying parameter a: b multiple large extreme events for $a=0.30$, c extreme events for $a=0.459$, d bounded chaos for $a=0.46$

Fig. 16

a Bifurcation diagram and time series for commensurate order $q=0.996,\omega =0.65$ and varying parameter b: b multiple large extreme events for $b=0.35$, c extreme events for $b=0.50$, d bounded chaos for $b=0.55$

Fig. 17

a Bifurcation diagram and time series for commensurate order $q=0.996,\omega =0.65$ and varying parameter c: b bounded chaos for $c=0.40$, c extreme events for $c=0.50$, d multiple large extreme events for $c=0.55$

3.3 Extreme events with respect to system parameters a, b, c and frequency $\omega$

In this part, we study the effect of forcing frequency $\omega$ and system parameters a, b, c on the extreme events for commensurate and incommensurate fractional-order forced Liénard system (3).

First, fixing $a=0.45,c=0.50,b=0.50,d=0.20$ and varying forcing frequency $\omega$ for the commensurate order $q = 0.996$, the bifurcation diagram is shown in Fig. 13. It can be seen here, the extreme events appear through two processes: intermittency and interior crisis. The intermittency route as shown when increasing $\omega$ in which a periodic oscillation bifurcates suddenly to a chaotic trajectory with large size at the critical point denoted by arrow L. The second process through interior crisis as shown when decreasing $\omega$ in which a small chaotic oscillation expands suddenly and randomly to a very large chaotic oscillation at an other critical point reached by arrow R. By comparing these results with the results found in the integer-order system [20], we remark that the same processes are obtained. However, in fractional-order system, other extreme events through intermittency occurred between the two critical points R and C which are not found in the integer case.

For $\omega =0.647$ (arrow L in Fig. 13) and $\omega =0.7055$ (arrow R in Fig. 13) , the obtained time series of fractional system (3) is presented in Fig. 14a and c, respectively, for short runs and the probability density function (PDF) of all the peaks $P_n$ is estimated with taking a long runs and it is shown in Fig. 14b (for $\omega =0.647$) and Fig. 14d ( for $\omega =0.7055$). It can be seen a long-tailed distributions confirming the existence of larger events exceeding the height $H_S$ (dashed vertical line). Furthermore, for the incommensurate orders, both the similar scenarios of extreme events are found: an interior crisis and intermittency.

Now, for the commensurate order $q = 0.996$, fixing $d=0.20,w=0.65$ and varying system parameters a, b, c, the bifurcation diagrams and time series of fractional system (3) are reported in Figs. 15, 16, and 17. Here, a transition from small- to large-amplitude chaotic oscillations is clearly observed through interior crisis with decreasing parameters a, b and with increasing parameter c . Thus, in this case, extreme events occur via an interior crisis. Also, the thresholds $H_S$ (the horizontal red lines in Figs. 15, 16, 17) are estimated numerically using the y(t) state variable to distinguish extreme events for all different cases which are mentioned in Table 3.

The PDF of all the peaks $P_n$ and the $H_S$ are estimated and illustrated in Fig. 18 for: $a=0.459$, $b=0.50$, and $c=0.50$. From Fig. 18, it can be seen long-tailed distributions confirming the existence of larger events exceeding the height $H_S$ (dashed vertical line). As a remark for the incommensurate system, the same results are found when varying $q_1$ and $q_2$.

3.4 Coexisting multiple extreme events

Recently, coexistence of attractors are found in fractional-order systems [30,31,32]. Coexistence of attractors appears when the system exhibits more than attractor for the same set of system parameters and taking different set of initial conditions. So, it is depending by the basin of attraction of the system.

Table 3 Dynamic cases with different values of a, b, and c

In Sect. 2, the fractional system (3) appeared existence of multistability too, but with coexisting of chaotic and quasiperiodic attractors. It interests if it is possible that the proposed fractional-order forced Liénard system can exhibit a multiple of coexisting attractors and, therefore, a multiple of extreme events. For this reason, we choose parameter set of initial conditions from the dissipative basin of attraction (BAD) of the forced Liénard system which is shown in Fig. 2. Space trajectories on $x-y$ plane and time series are plotted in Fig. 19 for three initial conditions: $(1,-0.5); (0,-0.5); (2;-0.5)$. It is found here that the fractional system (3) exhibits multistability and coexistence of multiple extreme events.

Fig. 18

Numerical PDF of $P_n$ for: a $a=0.459$, b $b=0.50$ and c $c=0.50$. Long-tail distribution exceeding the significant height $H_S$ in vertical red dashed lines

Fig. 19

Coexisting multiple extreme events for $q=0.993, \omega =0.65$ and different initial conditions: blue plot for $(1,-0.5)$, red plot for $(0,-0.5)$ and green plot for $(2,-0.5)$. a Coexisting multiple attractors with occasional large excursion of the trajectories in $x-y$ plane, b time series of fractional system (3) reveal the coexisting of multiple extreme events

4 Conclusion

We introduce a fractional system derived from a Liénard-type oscillator. Dynamics of the fractional system are studied. The system exhibits chaos, multistability, and extreme events. By varying parameters of the commensurate and incommensurate fractional-order cases, we have reported the effect of fractional-order derivative on the extreme events. Different tools such as bifurcation diagrams, Lyapunov exponents, extreme event qualifier $H_s$, and numerical PDFs have been applied. Interestingly, we have observed multistability and coexistence of multiple extreme events in such a fractional system exhibits. We believe that extreme events should be discovered further in fractional systems.