Investigation of $\varXi ^- nn$ ($S=-2$) hypernucleus in low-energy pionless halo effective theory

Abstract

We study the $\varXi ^- nn$ ($S=-2,\,I=3/2,\,J^P={1/2}^+$) three-body system using low-energy effective field theory (EFT). Due to the acute inadequacy of empirical information in this sector, there exists substantial degree of ambiguity in determining various few-body observables, some of which are expected to yield vital clues to resolving longstanding contentious issues in hypernuclear physics. Moreover, in astrophysical studies, a precise determination of neutron star equation of state (EoS) of putative hyperonic cores relies on essential input from the $S=-2$ sector. In this obscure current scenario, a pionless EFT analysis provides a systematic model-independent framework for assessing the feasibility of light three-particle-stable bound states, utilizing low-energy universality. Here we take recourse to a simplistic speculation of the three-body system by eliminating the repulsive spin-singlet $\varXi ^- n$ sub-system, while retaining the predominantly attractive (possibly bound) spin-triplet $\varXi ^- n$ and the virtual bound spin-singlet nn sub-systems. In particular, a qualitative leading order EFT investigation by introducing a sharp momentum ultraviolet cut-off parameter $\varLambda _{\mathrm{reg}}$ into the coupled integral equations indicates a discrete scaling behavior akin to a renormalization group limit cycle, thereby suggesting the formal existence of Efimov states in the unitary limit, as $\varLambda _{\mathrm{reg}}\rightarrow \infty$. Our subsequent non-asymptotic analysis indicates that the three-body binding energy $B_3$ is sensitively dependent on the cut-off without the inclusion of three-body contact interactions. Furthermore, our analysis reproduces several values of the binding energy $B_3\sim 3{-}4$ MeV, predicted in context of existing potential models, with the regulator $\varLambda _{\mathrm{reg}}$ in the range $\sim 350{-}460$ MeV. Finally, based on these model inputs for $B_3$, a ballpark estimate of the three-body scattering length in the range $2.6{-}4.9$ fm, is naively constrained by our EFT analysis. Despite approximations, the resulting Phillips line is expected to yield a robust feature of the halo-bound $\varXi ^- nn$ system. For pedagogical reasons, using a simple toy model interacting three-bosons system, we highlight in the appendices the typical universal features leading to emergence of RG limit cycle and Efimov states which are amenable to a low-energy EFT formalism.

Appendices

Efimov physics in low-energy EFT

For the sake of pedagogical completeness, we highlight aspects of the halo EFT analysis of two- and three-body universality responsible for formation of exotic Efimov-like states in fine-tuned three-body systems. Universality in this context refers to the property of distinct separation of scales, namely, similarities in long-range (low-energy) characteristics of a large class of multi-particle systems which are insensitive to the short-distance (high-energy) details. The halo-bound systems typically satisfying this property are naturally suited for a low-energy EFT description. We elucidate the pertinent EFT framework using the simplest system of three identical interacting spinless bosons ($B-B-B$), where additional involvement of spin and isospin degrees of freedom are absent. In particular, we consider a zero-range “toy-model” (ZRM) scenario (i.e., with two-body interaction range $r_0\rightarrow 0$) which motivates the general formalism of a leading order EFT analysis implemented in this paper. The foundations to this framework have been extensively discussed in the context of a large collection of pionless EFT (${}^{{\pi }\!\!\!/}$EFT) works in the literature (see, e.g., [2, 68, 72,73,74,75,76,77,78,79,80,81,82,83] and references therein). For the ensuing discussions below, we closely follow the reviews works [68, 83, 117].

1.1 Two-body sector

The two-body dynamics stems from the most general non-relativistic effective Lagrangian constituting all possible local short-range S-wave two-body interactions of the generic form [75,76,77,78,79]

$$\begin{aligned} {\mathscr {L}}^{\mathrm{(KSW)}}_{2}= & {} B^\dagger \bigg [i\partial _t+\frac{\nabla ^2}{2m_B}\bigg ]B -\frac{C_0}{4}\left( B^{\dagger }B\right) ^2\nonumber \\&-\frac{C_2}{4}\left[ \nabla (B^{\dagger }B)\right] ^2 +\cdots , \end{aligned}$$

(23)

where the ellipses denote higher order derivative terms and $C_{0,2,\ldots }$ are two-body coupling constants. These couplings may be fixed from the empirical knowledge of the two-body parameters, such as those occurring in the well-known Bethe’s Effective Range Expansion (ERE) formula for the S-wave scattering phase-shift $\delta _0$, namely,

$$\begin{aligned} k\cot \delta _0 = -\frac{1}{a_0}+\frac{r_0}{2} k^2+\mathcal {O}(k^4)\,, \end{aligned}$$

(24)

with k being the center-of-mass scattering momentum of the two-boson ($B-B$) system. Especially, in the vicinity of shallow two-body (real or virtual) bound states these couplings are subject to an unnatural scaling with the magnitude of the S-wave scattering length ($a_0$) becoming unusually large in comparison to the short-distance effective range ($r_0$) of the interactions. In this case the theory becomes approximately conformally invariant, leading to a peculiar EFT governed by a non-trivial RG fixed point of the scale-dependent couplings [82].

Fig. 8

The leading order two-body S-wave scattering amplitude $T^{(0)}_2$, obtained by resumming of the “bubble” graphs containing the $C_0$ interaction. It is compactly represented as a Lippmann–Schwinger integral equation, ${{\hat{T}}}^{(0)}_2={{\hat{V}}}_2+ {{\hat{V}}}_2 {{\hat{G}}}_0 {{\hat{T}}}^{(0)}_2$

Consider Q to be a generic small momentum associated with a certain emergent low-energy scale $\gamma _0$ of the two-body system, and $M_{hi}$ as the UV cut-off or the breakdown scale of the theory associated with the unresolved “heavy” pion mass $m_\pi$. Then, the unnatural scaling scenario implies $k \sim Q\sim \gamma _0 \sim 1/|a_0| \ll M_{hi}\sim 1/r_0$. This is distinguished from the natural scenario where the interaction range $r_0\sim 1/m_\pi$ solely accounts for all relevant scales such that $k \sim Q\sim \gamma _0 \sim 1/|a_0| \sim M_{hi}\sim 1/r_0$. Such unnatural two-body systems are ubiquitous in nuclear physics, say, in the case of two neutrons, $a_{nn}= -18.63~\mathrm{fm}\gg r_{nn}\sim 1/m_\pi \sim 0.5~\mathrm{fm}$. In all these manifestly fine-tuned scenarios near-threshold (shallow) bound dimer states emerge by critically tuning the couplings according to

$$\begin{aligned} C_{2r} \sim \frac{1}{2\mu _B M^r_{hi} Q^{r+1}} \quad \forall \, r\in {{\mathbb {Z}}}_+ \end{aligned}$$

(25)

with $\mu _B=m_B/2$ being the reduced mass of the two-boson ($B-B$) system. This kind of two-body contact interactions scaling rule is termed as the Q-counting [76,77,78,79,80]. Based on the Q-counting different components of Feynman amplitudes scale as follows:

• the non-relativistic boson propagator, namely,

  $$\begin{aligned} iS_B(p)=\frac{i}{p_0-\frac{\mathbf{p}^2}{2m_B}+i\eta }, \end{aligned}$$

  (26)

  scales as $\sim m_B/Q^2\sim {{\mathcal {O}}}(Q^{-2})$,

• the loop integral scales as $\sim \mathcal {O} (Q^5)$, ¹⁰

• the interaction vertices $C_{2r}\nabla ^{2r}$ scale as $\sim \mathcal {O} (Q^{r-1})$.

Accordingly, all two-body Feynman graphs contributing up to a fixed order in the counting, say $\mathcal {O} (Q^N)$, with L loops and ${{\mathcal {V}}}_{2r}$ interaction vertices with 2r derivatives scale as [117]

$$\begin{aligned} T^{(N)}_2= & {} \sum ^N_{\nu = -1} T_2^{(\nu )},\quad T_2^{(\nu )}\sim \mathcal {O} (Q^\nu )\,; \quad \nonumber \\ \nu= & {} 3L+2+\sum _{r=0}(r-3){{\mathcal {V}}}_{2r}\ge -1\,. \end{aligned}$$

(27)

Thus, for example, at low energies $E\sim 1/a^2_0$, restricting to leading order in Q-counting (i.e., for $N=-1$), an infinite number of loops with only $C_0$ interactions are needed to be non-perturbatively resummed. Such an infinite sequence of “bubble diagrams”, all contributing at the same order in the Q-counting (cf. Fig. 8), yields a shallow two-body bound state. However, at the next order (i.e., for $N=0$) the $C_2$ interactions contribute to the dynamics. Being $1/M_{hi}$ suppressed compared to the leading $C_0$ interactions, the $C_2$ constitutes a perturbative correction. Such a “bubble resummation” with only the $C_0$ interaction leads to a Lippmann–Schwinger series for the two-body scattering amplitude $T^{(0)}_2$ which may be expressed as an integral equation:

$$\begin{aligned} T^{(0)}_2(E)= & {} -C_0 - \frac{1}{2}C_0 \int \frac{d^4q}{(2\pi )^4 i}\, \frac{i}{q_0-\mathbf{q}^2/2m_B+i\eta }\, \nonumber \\&\times \frac{i}{E-q_0-\mathbf{q}^2/2m_B+i\eta }\,T^{(0)}_2(E)\,, \end{aligned}$$

(28)

where $q_0$, $\mathbf{q}$ are temporal and spatial parts of loop four-momentum q. The integral equation may be regularized using a sharp momentum cut-off $\varLambda _{\mathrm{reg}}$ and subsequently solving to obtain

$$\begin{aligned} T^{(0)}_2 (E,\varLambda _{\mathrm{reg}}) = -C_0 \left[ 1+\frac{\mu _B C_0}{2\pi ^2}\left( \varLambda _{\mathrm{reg}} -\frac{\pi }{2}\sqrt{-2\mu _B E-i\eta }\right) \right] ^{-1}.\nonumber \\ \end{aligned}$$

(29)

The renormalization of the amplitude $T^{(0)}_2(E)$ can be implemented by matching to the two-body S-wave scattering length using the relation

$$\begin{aligned} a_0 =-\frac{\mu _B}{4\pi } \lim _{k\rightarrow 0} T^{(0)}_2(E=\mathbf{k}^2/2\mu _B)\,, \end{aligned}$$

(30)

leading to the regulator-dependent result for the coupling $C_0$, namely,

$$\begin{aligned} C_0(\varLambda _{\mathrm{reg}}) = \frac{4\pi a_0}{\mu _B} \left( 1-\frac{2a_0\varLambda _{\mathrm{reg}}}{\pi }\right) ^{-1}\,, \end{aligned}$$

(31)

such that the renormalized scattering amplitude is given by

$$\begin{aligned} T_2 (E) = \frac{4\pi }{\mu _B} \frac{1}{-1/a_0+\sqrt{-2\mu _B E-i\eta }}\,. \end{aligned}$$

(32)

Auxiliary field formalism  In the context of studying three-body dynamics with two-body bound subsystems with large scattering lengths, it is convenient to introduce auxiliary dimer fields or dimerons (d). Ideally, the bare auxiliary fields do not propagate and even have a “wrong sign” in the kinetic terms (see following two-body Lagrangian). Hence, the content of the original theory remains unchanged by the addition of such ghost fields “by hand”. For the present case of the spinless three-boson system ($B-B-B$), an alternative two-body Lagrangian in terms of the dimeron fields can be constructed as [72,73,74],

$$\begin{aligned} {\mathscr {L}}^{\mathrm{(BHvK)}}_2= & {} B^{\dagger }\bigg [i\partial _t+\frac{\nabla ^2}{2m_B}\bigg ]B -d^{\dagger }\bigg [i\partial _t+\frac{\nabla ^2}{4m_B}-\varDelta _d\bigg ]d\nonumber \\&-y_0 \! \left( d^{\dagger }B^2+B^{\dagger 2} d\right) +\cdots {.}\,\quad \, \end{aligned}$$

(33)

In effect, the dimerons are essentially employed to cancel the quadratic terms such as $(B^{\dagger }B)^2$ in Eq. (23), so that all interactions between the B fields are now mediated via the dimer exchange process, with $y_0$ as the corresponding interaction coupling. The quantity $\varDelta _d$ is a free parameter related to the binding energy of the dimeron d such that the bare or tree-level dimeron propagator is the simple non-dynamical term $i/\varDelta _d$. Quantum loop corrections, however, allow the dimerons to propagator. It is notable that by virtue of reparametrization invariance of the theory, the above Lagrangian can be shown to be equivalent to the original two-body Lagrangian, Eq. (23).

In the context of halo EFT where the dimeron formalism has been extensively used, the Q-counting scheme has been extended to include the scaling,

$$\begin{aligned} y^2_0\sim \frac{M_{hi}}{4\mu ^2_B}\sim {{\mathcal {O}}}(1) \quad \text {and} \quad \varDelta _d\sim \frac{M_{hi} Q}{2\mu _B}\sim {{\mathcal {O}}}(Q).\nonumber \\ \end{aligned}$$

(34)

Consequently, using field re-definitions in trading away the time derivatives in favor of space derivatives, the kinetic term becomes sub-leading compared to term proportional to $\varDelta _d$. In that case the Q-counting leads to an infinite sequence of Feynman graphs (similar to the ones displayed in Fig. 1), each contributing at the same order as the static dimeron propagator i$\varDelta ^{-1}_d \sim {{\mathcal {O}}}(Q^{-1})$. Consequently, they must all be resummed at the leading order to yield the full dynamical “dressed” dimeron propagator:

$$\begin{aligned} i\varDelta ^{(0)}(p_0,\mathbf{p})= & {} \frac{i\pi }{y^2_0 \mu _B} \left[ \frac{\pi \varDelta _d}{y^2_0 \mu _B}+\frac{2}{\pi }\varLambda _{\mathrm{reg}}\nonumber \right. \\&\left. -\sqrt{-2\mu _B p_0+\mathbf{p}^2/4-i\eta }\right] ^{-1}. \end{aligned}$$

(35)

We note its similarity to the resummed two-body scattering amplitude, Eq. (29), with the two-body center-of-mass kinetic energy $E\rightarrow p_0-\mathbf{p}^2/(8\mu _B)$, where $p_0 (\mathbf{p})$ is kinetic energy (momentum) of the dimeron. Upon renormalization using Eq. (31) and the leading order relation among the two-body parameters, namely, $C_0 \rightarrow 4y^2_0/\varDelta _d$, the renormalized dressed dimeron propagator becomes

$$\begin{aligned} i\varDelta (p_0,\mathbf{p}) = -\frac{i\pi }{y^2_0 \mu _B} \left[ -\frac{1}{a_0}+\sqrt{-2\mu _B p_0+\mathbf{p}^2/4-i\eta }\right] ^{-1}. \nonumber \\ \end{aligned}$$

(36)

If scattering length $a_0>0$, then the above dimeron propagator has a pole at $p_0 = -1/(2\mu _B a^2_0) + \mathbf{p}^2/(8\mu _B)$. For low-energy threshold processes, $\mathbf{p}\rightarrow 0$ and $p_0\rightarrow -{{\mathcal {B}}}_2=-1/(2\mu _B a^2_0)$, in which case the renormalized dimeron propagator has a residue (wave function renormalization constant) at the pole given by

$$\begin{aligned} {{\mathcal {Z}}}_d = \left[ \frac{\mathrm{d}\varDelta ^{-1}_d(p_0,\mathbf{0})}{\mathrm{d}p_0}\right] ^{-1}_{p_0=-{{\mathcal {B}}}_2} =\frac{2\pi }{y^2_0\mu ^2_B a_0}\,. \end{aligned}$$

(37)

1.2 Three-body sector

Fig. 9

Diagrammatic representation of the three-body integral equation for the spinless three-boson S-wave scattering amplitude $T^{(0)}_3$. In the Q-counting scheme, all graphs in the first line contribute as $\sim M_{hi}/(2\mu _B Q^2)$, while those in the second line with three-body contact interactions contribute as $\sim 1/(2\mu _B Q^4)$. The single line denotes a boson (B) propagator, the double line denotes a static dimeron (d) propagator, and the double line with an oval blob represents a fully dressed (dynamical) renormalized dimeron propagator. Finally, the dark filled circle represents an insertion of a leading order three-body contact interaction

Here we describe the dynamics associated with S-wave scattering of the three-boson system depicted in Fig. 9. Excluding the genuine three-body interaction (3BF) diagrams shown in the second row, the scattering diagrams in the first row constitute only the two-body interaction $y_0$, and thus described by same leading order EFT Lagrangian, Eq. (33). Under the Q-counting scheme, a simple investigation shows that these diagrams contribute at the same order. For example, the tree level diagram in first row can be considered as a one-boson (B) exchange process between the incoming and outgoing dimerons (d). Since the tree diagram containing two dBB vertices ($y^2_0\sim M_{hi}/4\mu _B^2$) and one B propagator ($iS_B\sim m_B/Q^2$), this amounts to a net contribution of order $\sim M_{hi}/(2\mu _B Q^2)$. The adjacent one-loop re-scattering diagram contains two additional dBB vertices, two additional B propagators, a dimeron propagator ($i\varDelta \sim 2\mu _B/M_{hi} Q$), and a loop integral ($\sim Q^5/2\mu _B$). This implies that the one-loop diagram also scales as $\sim M_{hi}/(2\mu _B Q^2)$, like the tree graph. In fact, inspection shows that every re-scattering graph in the first row precisely contributes at the same leading order, necessitating a resummation of all such graphs. Besides, one also requires the infinite sequence of 3BF diagrams (second row) which may be shown to contribute at the leading order, and hence needed to be resummed as well. The power counting for such graphs is described later in this section. However, unlike the resummation in the two-body sector [cf. Eq. (28)] which amounts to a simple summation of a geometric series, the same is impracticable in the three-body sector. In contrast, here we must incorporate a non-perturbative resummation in the form of a “one-loop” Fredholm integral equation (third row of Fig. 9) which is solved self-consistently for the scattering amplitude $T^{(0)}_3$ using numerical methods. It is notable that the standard Faddeev equations¹¹are a set of coupled integro–differential equations in the co-ordinate representation. They are numerically solved using finite range model potentials with well-defined kernels in the Hilbert-Schmidt class. Our ZRM integral equations in contrast have an ill-defined kernel stemming from the non-self-adjoint character of the underlying three-body Hamiltonian [84, 85, 119, 120]. Such “Faddeev-like” zero range three-body integral equations in the momentum representation are termed as the STM or the so-called Skornyakov–Ter–Martirosyan equations [69,70,71]. Despite the ambiguities in their solution, the STM equations have the primary advantage of fitting naturally into an EFT framework based on a diagrammatic or Lagrangian-based approach. This contrasts with the inherently non-perturbative Hamiltonian-based potential model approach for solving three-body Faddeev equations.

The biggest advantage, however, lies in the manner of introducing 3BF which is quite naturally achieved in the STM framework without the requirement of ad hoc three-body potentials. The ambiguity in the Hamiltonian is solved by cutting off the effective interactions at short-distances. This is accomplished in the EFT by introducing, e.g., a sharp momentum cut-off $\varLambda _{\mathrm{reg}}$ in the integral equations which becomes a free parameter of the theory. This regularization method implicitly necessitates the introduction of cut-off-dependent three-body couplings needed to renormalize the artificial cut-off dependence of the STM equations. To this end, we introduce additional non-derivatively coupled three-body interactions in the effective Lagrangian, for instance,

$$\begin{aligned} {\mathscr {L}}^{\mathrm{(KSW)}}_{3}= & {} \frac{D_0(\varLambda _{\mathrm{reg}})}{36} (B^\dagger B)^3 +\cdots , \quad \text {(standard form)} \nonumber \\ {\mathscr {L}}^{\mathrm{(BHvK)}}_{3}= & {} -\,d_0(\varLambda _{\mathrm{reg}}) \left( d^\dagger d\right) \left( B^\dagger B\right) +\cdots , \quad \text {(dimerized form)} \nonumber \\ \end{aligned}$$

(38)

with the contact interaction couplings scaling unnaturally at the leading order, namely, $D_0\sim d_0 \sim 1/(2\mu _B Q^4)$. In this case the $B-B-B$ system exhibits three-body (Efimov) universality.¹² The values of the 3BF couplings can be fixed using additional three-body datum (e.g., three-body binding energy) in realistic situations. The ellipses denote derivative 3BF terms which are naturally subleading. Figure 9 (second row) displays all re-scattering diagrams with insertions of leading order three-body contact interactions. These graphs are similarly resummed into an integral equation that yields contributions of order $\sim 1/(2\mu _B Q^4)$, and hence equally important as the set of graphs in the first row with two-body interactions only. Together they constitute all possible non-perturbative contributions to the scattering amplitude at leading order.

Assuming the manifestation of Efimov universality, the natural choice of the reference frame is the boson-dimeron ($B-d$) center-of-mass (CM), with the relative external momenta being $\mathbf{-k,k}$ ($\mathbf{-p,p}$) for the incoming (outgoing) boson and dimeron respectively. With the total three-body CM kinetic energy as E, their energies are taken as $E_A,\, E-E_A$ ($E'_A,\, E-E'_A$) for the incoming (outgoing) particles. Using standard Feynman rules which follow from the EFT Lagrangians, Eqs. (33) and (38), we easily obtain the following Faddeev-like STM integral equation for the unrenormalized scattering amplitude $T^{(0)}_3$ corresponding to the second line of Fig. 9, namely,

$$\begin{aligned}&T^{(0)}_3\left( \mathbf{p,k};E\right) = -\left[ \frac{4y^2_0}{E-E'_A-E_A-(\mathbf{p+k})^2/2m_B +i\eta }\right. \nonumber \\&\quad \left. +d_0(\varLambda _{\mathrm{reg}})\right] \nonumber \\&\quad +\, \frac{i\pi }{\mu _By^2_0}\int ^{\varLambda _{\mathrm{reg}}} \frac{\mathrm{d}^4q}{(2\pi )^4} \bigg [\frac{4y^2_0}{E-E'_A-q_0- (\mathbf{p+q})^2/2m_B+i\eta }\nonumber \\&\quad + d_0(\varLambda _{\mathrm{reg}})\bigg ] \nonumber \\&\quad \times \, \frac{1}{q_0-\mathbf{q}^2/2m_B +i\eta }\, \frac{T^{(0)}_3\left( \mathbf{q,k};E\right) }{1/a_0-\sqrt{-2\mu _B(E-q_0)+\mathbf{q}^2/4-i\eta }},\nonumber \\ \end{aligned}$$

(39)

where $q_0 (\mathbf{q})$ is the temporal (spatial) part of loop momentum with the three-momentum integral cut-off in the UV region at $|\mathbf{q}| = \varLambda _{\mathrm{reg}}$. Using Cauchy’s residue theorem, the integral over $q_0$ can be evaluated by choosing the pole, $q_0=\mathbf{q}^2/2m_B$, making one of the boson propagators inside the loop integration on-shell. Further simplifications is achieved by choosing either one or both the initial and final states on-shell. For instance, with the full on-shell choice $E_A = \mathbf{k}^2/2m_B$ and $E'_A= \mathbf{p}^2/2m_B$, we obtain

$$\begin{aligned} T^{(0)}_3\left( \mathbf{p,k};E\right)= & {} -4m_By^2_0 \left[ \frac{1}{m_B E-(\mathbf{p}^2+\mathbf{p \cdot k}+\mathbf{k}^2)+i\eta }\right. \nonumber \\&\left. +\frac{d_0(\varLambda _{\mathrm{reg}})}{4m_By^2_0}\right] \nonumber \\&-\, 8\pi \int ^{\varLambda _{\mathrm{reg}}} \frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3} \bigg [\frac{1}{m_B E-(\mathbf{p}^2+\mathbf{p \cdot q}+\mathbf{q}^2)+i\eta } \nonumber \\&+\frac{d_0(\varLambda _{\mathrm{reg}})}{4m_By^2_0}\bigg ] \nonumber \\&\times \, \frac{ T^{(0)}_3\left( \mathbf{q,k};E\right) }{-1/a_0+\sqrt{-2\mu _B E+3\mathbf{q}^2/4-i\eta }}\, . \end{aligned}$$

(40)

Especially in the context of S-wave scattering process, we consider the projection of the unrenormalized amplitude onto the $l=0$ partial wave renormalized amplitude given by

$$\begin{aligned} T_3\left( p,k;E\right) \equiv \frac{{{\mathcal {Z}}}_d}{2} \int _{-1}^1 \mathrm{d} \left( \cos \theta _{\hat{\mathbf{p}}\cdot \hat{\mathbf{q}}}\right) \,\,T^{(0)}_3\left( \mathbf{p,k};E\right) \,, \nonumber \\ \end{aligned}$$

(41)

such that boson-dimeron elastic scattering amplitude is obtained by evaluating the renormalized scattering amplitude at the on-shell point, $p=|\mathbf{p}|=k=|\mathbf{k}|$ and $E=-{{\mathcal {B}}}_2+3k^2/(4m_B)$, with dimer binding energy ${{\mathcal {B}}}_2=1/(2\mu _Ba^2_0)$. Furthermore, in the threshold limit one obtains the three-body scattering length as

$$\begin{aligned} a^{\mathrm{(Bd)}}_3= -\frac{m_B}{3\pi }\lim _{k\rightarrow 0}\,\, T^{(0)}_3\bigg (k,k;\frac{3k^2}{4m_B}-{{\mathcal {B}}}_2\bigg )\,. \end{aligned}$$

(42)

It is conventional to re-define the dimension-full three-body coupling $d_0(\varLambda _{\mathrm{reg}})$ in terms of a dimensionless coupling $H(\varLambda _{\mathrm{reg}})$ such that $T^{(0)}_3(p,k;E)$ has a well-defined asymptotic behavior as $\varLambda _{\mathrm{reg}} \rightarrow \infty$, namely,

$$\begin{aligned} d_0(\varLambda _{\mathrm{reg}}) = -\frac{4m_By^2_0}{\varLambda ^2_{\mathrm{reg}}} H(\varLambda _{\mathrm{reg}})\,. \end{aligned}$$

(43)

This leads to the 3BF renormalized STM integral equation for the three-boson system, originally derived in Ref. [74]:

$$\begin{aligned} T_3(p,k;E)= & {} \frac{8\pi }{\mu _B a_0}\left[ \frac{1}{2pk}\ln \left( \frac{p^2+k^2+pk-m_B E-i\eta }{p^2+k^2-pk-m_B E-i\eta }\right) \right. \nonumber \\&\left. +\frac{H(\varLambda _{\mathrm{reg}})}{\varLambda ^2}\right] \nonumber \\&+\,\frac{4}{\pi }\int _0^{\varLambda _{\mathrm{reg}}} dq\,\, q^2\left[ \frac{1}{2pq}\ln \left( \frac{p^2+q^2+pq-m_B E-i\eta }{p^2+q^2-pq-m_B E-i\eta }\right) \right. \nonumber \\&\left. +\frac{H(\varLambda _{\mathrm{reg}})}{\varLambda ^2}\right] \nonumber \\&\times \, \frac{T_3(q,k;E)}{-1/a_0+\sqrt{3q^2/4-\mu _B E-i\eta }}. \end{aligned}$$

(44)

The above equation must be numerically solved to obtain the three-body eigenenergies and scattering lengths in the respective kinematical domains.¹³ In this case the STM equation is one-dimensional in the sense that $B-d$ scattering involves a single channel elastic process $B+d\rightarrow B+d$. In realistic situations with non-zero spin–isospin degrees of freedom, the processes involve coupled elastic and inelastic channels, thereby requiring multi-dimensional representations. For instance, the $\varXi ^- nn$ ($I=3/2,\, J^P={1/2}^+$) system dealt in this paper involves a system of three coupled-channel scattering processes: the elastic channel $n+(\varXi ^-n)_t\rightarrow n+(\varXi ^-n)_t$, and the two inelastic channels $n+(\varXi ^-n)_t\rightarrow n+(\varXi ^-n)_s$ and $n+(\varXi ^-n)_t\rightarrow \varXi ^-+(nn)_s$, where the subscripts represent the sub-system spins. However, for the sake of simplicity the former inelastic channel involving the spin-singlet dimer $(\varXi ^-n)_s$ is assumed to be decoupled (see text). Consequently, we deal with a reduced system of two coupled-channel integral equation in terms of the half-on-shell amplitudes $t^{(R)}_{A,B}$ (cf. Appendix B). Moreover, additional re-coupling coefficients are necessary for projecting each of the scattering diagrams onto the correct spin–isospin channels.

1.3 RG limit cycle

With sufficiently large $B-B$ scattering length, i.e., $a_0\rightarrow \infty$, and very short range two-body interactions, $r_0\rightarrow 0$, three-body or Efimov universality implies the existence of a tower of arbitrarily-shallow three-body bound states close to the unitary or resonant limit as $\varLambda _{\mathrm{reg}}\rightarrow \infty$. This remarkable discovery is credited to Vitaly Efimov [86,87,88], who in 1970 demonstrated that the system of three identical bosons interacting via attractive (i.e, with $a_0>0$) inverse square channel potential $V \sim -\left( s^2_0+1/4\right) / \mu _B R^2$ becomes resonant. By solving the Faddeev equations using the well-known hyperspherical representation in coordinate space with suitable short-distance adiabatic boundary conditions, a geometric sequence of three-particle level states (Efimov states) was obtained. The corresponding binding energies $B^{(n)}_3$ were found to lie approximately within the interval,

$$\begin{aligned} \frac{1}{2\mu _B a^2_0} \lesssim B^{(n)}_3 {\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} \frac{\kappa ^2_*}{2\mu _B} \left( e^{-2\pi /s_0}\right) ^{(n-n_*)} \lesssim \frac{1}{2\mu _B r^2_0}\,,\nonumber \\ \end{aligned}$$

(45)

where $n=n_*$ is some integer labeling for a reference level with binding momentum $\kappa _*$, determined by the Efimov spectrum in the (asymptotic) unitary limit. The multiplicative factor $\lambda _0 \equiv e^{\pi /s_0}$ is an universal parameter which depends only on the gross features of the three-body system, such as the mass ratios of the bound particles and the overall quantum statistics of the system, irrespective of the fine details such as the nature of the individual bound particles and the short-distance interaction potentials. In this case, $s_0=1.00624\ldots$ is obtained as a solution to the transcendental equation

$$\begin{aligned} s_0\cosh \frac{\pi s_0}{2}=\frac{8}{\sqrt{3}}\sinh \frac{\pi s_0}{6}\,. \end{aligned}$$

(46)

It is notable that mass ratios play the most crucial role in deciding the typical estimate for $s_0$. However, the spin, isospin and other possible internal quantum numbers of the gross three-body system can fine-tune its precise value. Moreover, away from unitarity in the non-resonant domain as $a_0\sim r_0$, the value of $s_0$ is likely to change from its asymptotic value due to cut-off and other low-energy parametric dependencies thereby becoming non-universal. For instance, the three-nucleon ($N-N-N$) iso-doublet S-wave systems of triton and helion (${}^{3}$H, ${}^{3}$He) in the $I=J=1/2$ channel, are probably the best known examples of realistic Efimov-bound states in nuclear physics having identical asymptotic scale parameter $s_0$ and Efimov spectrum (neglecting Coulomb interactions) as in the case of the $B-B-B$ system.

Fig. 10

Demonstration of RG limit cycle. Left panel: Discrete scaling behavior found in Russian nesting dolls with sizes of successive dolls decreasing by a constant factor $\sim 1.5$. Right panel: The regulator scale $\varLambda _{\mathrm{reg}}$ dependence of the three-body coupling $H(\varLambda _{\mathrm{reg}})$ for the $B-B-B$ system. The input three-body datum is the scattering length $a^{\mathrm{(Bd)}}_3=1.56 a_0$. The parameters, $\varLambda _*$ and $\varLambda _0$, are obtained by fitting Eq. (52) (solid curve) to the data points obtained by numerically solving the STM Eq. (44), reproducing the result of Ref. [74]

The above-mentioned behavior of the three-body system in the so-called scaling limit ($r_0\rightarrow 0$) is an indication that the familiar continuous scaling symmetry (conformal invariance) under the scale transformation

$$\begin{aligned} a_0 \rightarrow \lambda a_0 \qquad \text {and} \qquad E_{\mathrm{2-body}}\rightarrow \lambda ^{-2} E_{\mathrm{2-body}}, \nonumber \\ \end{aligned}$$

(47)

where $\lambda \in {{\mathbb {R}}}_+$ is an arbitrary constant, gets evidently broken in the three-body sector into the discrete scaling subgroup of scale transformations given by

$$\begin{aligned}&\kappa _* \rightarrow \kappa _*\, \,\,\, a_0\rightarrow \lambda ^{n}_0 a_0\,, \,\,\, E\rightarrow \lambda ^{-2n}_0 E,\,\,\,\nonumber \\&\quad \text {where}\,\,\, \lambda _0=e^{\pi /s_0}\approx 22.7\,. \end{aligned}$$

(48)

This feature can be attributed to the introduction of the parameter $\kappa _*$ which sets a new relevant scale in the three-body system, in addition to the only existing relevant scale set by the two-body parameter $a_0\rightarrow \infty$ close to the unitary limit. This leads to logarithmic scaling violation of low-energy observables which must scale as some log-periodic function $\sim f\left[ s_0\ln (\kappa _*|a_0|)\right]$ . In other words, the expected non-trivial RG fixed point scaling of the 3BF couplings breaks down into that of an UV RG limit cycle discrete scaling characterized by the parameter $\lambda _0$. This unusual type of RG arises in other branches of physics as well, such as in condensed matter (see, e.g., Refs. [121,122,123,124,125]), or in the study of turbulence and complex systems (see e.g., Ref. [126]). Curiously enough, such a discrete scaling behavior bears close resemblance to the well-known Russian Matryoshka dolls, as displayed in Fig. 10. They consist of an assembly of hollow wooden dolls of decreasing size nested one within the other such that the ratio of the sizes of successive dolls remains approximately constant, for instance, as shown in the figure, the discrete scaling factor is given by

$$\begin{aligned} e^{2\pi /s^{\mathrm{(doll)}}_0} \approx \frac{\mathrm{doll}^{(n)}}{\mathrm{doll}^{(n+1)}} \approx 1.5\,. \end{aligned}$$

(49)

Likewise, in proximity to the unitary limit, the ratio of the successive binding energies of the of $B-B-B$ Efimov trimer levels scale as $B^{(n)}_3/B^{(n\!+\!1)}_3 \!\approx \! e^{2\pi /s_0}\!\approx \! 515$. The approximate relation becomes an exact one only in the unitary limit with $a_0=\infty$.

The RG limit cycle features associated with Efimov spectrum are deduced quite naturally in low-energy EFT by studying the cut-off regulator dependence of the 3BF coupling $H(\varLambda _{\mathrm{reg}})$ via the STM integral Eq. (44). The introduction of UV regulator $\varLambda _{\mathrm{reg}}$ repairs the non-self-adjoint pathology associated with the STM equation making the scattering amplitude $T_3$ well-behaved asymptotically. But this comes at a cost: the continuous scaling symmetry gets partially broken, leading to the emergence of an RG limit cycle. This feature can be checked analytically by investigating the asymptotic nature of the integral equation in the unitary and scaling limits. In other words, with p taken as the off-shell (outgoing) momentum having the same order of magnitude as the loop momenta q, we examine the integral equations in the limit $E,1/|a_0|,k \ll p\sim q \sim \varLambda _{\mathrm{reg}} \lesssim \infty$, whereby the 3BF terms $\propto H(\varLambda _{\mathrm{reg}})/\varLambda ^2_{\mathrm{reg}}$ may be dropped. To that effect, the asymptotic solution for $T_3$ scales as a pure power-law with an undetermined exponent, $T_3 (p)\sim p^{s-1}$. Thus, the resulting STM Eq. (44) becomes

$$\begin{aligned} p^{s-1} = \frac{4}{\sqrt{3}\pi p}\int _0^{\infty } \mathrm{d}q \,\,q^{s-1}\ln \frac{p^2+pq+q^2}{p^2-pq+q^2}\,, \end{aligned}$$

(50)

which after a change of variable, $q=xp$, becomes

$$\begin{aligned} 1 = \frac{4}{\sqrt{3}\pi } \int _0^{\infty } dx \,\, x^{s-1} \ln \frac{1+x+x^2}{1-x+x^2}\,. \end{aligned}$$

(51)

A Mellin transformation finally reduces the STM equation to the very aforementioned transcendental relation, Eq. (46), obtained by solving the low-energy Faddeev equation, albeit with a complex exponent $s=\pm is_0$, where $s_0=1.00624\ldots$ is obtained in this case. The asymptotic value $s_0$ parametrizes the exact discrete scaling behavior at the unitary limit, formally indicating the manifestation of Efimov effect. Furthermore, Bedaque et al. [74] deduced an approximate analytical expression for the typical log-periodic running of dimensionless three-body coupling $H(\varLambda _{\mathrm{reg}})$, given by

$$\begin{aligned} H(\varLambda _{\mathrm{reg}}) = -\frac{\sin \left[ s_0 \ln (\varLambda _{\mathrm{reg}}/\varLambda _*) -\arctan (1/s_0) \right] }{\sin \left[ s_0 \ln (\varLambda _{\mathrm{reg}}/\varLambda _*)+\arctan (1/s_0) \right] }.\nonumber \\ \end{aligned}$$

(52)

Such an RG orbit for the coupling constant with a periodic dependence on the cut-off parameter when the latter increases to infinity is termed as a limit cycle. The underlying principle ensures that the family of effective theories with finite cut-offs yields predictions which are guaranteed to remain independent of the respective cut-offs. In the above expression $\varLambda _*$, in analogy to $\kappa _*$, is an emergent three-body dynamical parameter which results from the logarithmic scaling violation $\sim \ln (\varLambda _*|a_0|)$. This parameter is likewise fixed using a three-body datum, such as the trimer binding energy $B_3$ or the $B-d$ scattering length $a^{\mathrm{(Bd)}}_{3}$. Alternatively, the scale dependence of $H(\varLambda _{\mathrm{reg}})$ may be determined by numerically solving the STM Eq. (44) at non-asymptotic scales for a given two-body input $a_0$ and three-body datum (e.g., $B_3,\,a_3^{(Bd)}$, etc.). In Fig. 10, we reproduce the result of Ref. [74], displaying the approximate RG limit cycle with quasi-periodic singularities associated with the successive formation of new Efimov states as $\varLambda _{\mathrm{reg}}\rightarrow \infty$. The data points correspond to our numerical evaluations, while the solid curve is the fit to these data using the analytical formula of Bedaque et al., Eq. (52). To this end, one may extract the three-body parameters, such as $\varLambda _*$ and $s_0$, using the momentum scaling relations,

$$\begin{aligned} \varLambda _n=\left( e^{\pi /s_0}\right) ^n \varLambda _0 \quad \text {as}\,\, n\rightarrow \infty \,, \end{aligned}$$

and

$$\begin{aligned} \varLambda _0= \exp \left[ \frac{\arctan (1/s_0)}{s_0}\right] \varLambda _* \,, \end{aligned}$$

(53)

where $\varLambda _{\mathrm{reg}}= \varLambda _n$ represents the $n^{\mathrm{th}}$ zero of the three-body coupling $H(\varLambda _n)$. The typical non-asymptotic values of $s_0$ expected in this case depend on $\varLambda _n$, and hence differ from the cutoff-independent asymptotic value, $s_0 \rightarrow 1.00624\ldots$, which restores the exact scaling symmetry of the STM equation as $\varLambda _n\rightarrow \infty$.

Integral equation for $\varXi ^-nn$ ($I=3/2, J^P={1/2}^+$) system

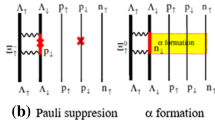
The Faddeev-like three-body coupled integral equation for the $n+(\varXi ^- n)_t\rightarrow n+(\varXi ^- n)_t$ elastic scattering amplitude $t_A$ (cf. Fig. 2) (excluding the $(\varXi ^-n)_s$ singlet subsystem channel) can be easily obtained via Feynman rules from the non-relativistic effective Lagrangian, and is given as

$$\begin{aligned} t_A \left( \mathbf{p,k};E\right)= & {} (-y_1^2)\left[ {{\mathcal {C}}}^{(11)}_2 S_{\varXi }\left( E-\frac{\mathbf{p}^2}{2M_n}-\frac{\mathbf{k}^2}{2M_n},\mathbf{p+k}\right) \right. \nonumber \\&\left. +{{\mathcal {C}}}^{(11)}_3\frac{M_{\varXi }}{2}\frac{g_3(\varLambda _{\mathrm{reg}})}{\varLambda ^2_{\mathrm{reg}}} \right] \nonumber \\&-\, {{\mathcal {C}}}^{(11)}_2 (-y_1^2)\int ^{\varLambda _{\mathrm{reg}}} \frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3}\, t_A\left( \mathbf{q,k};E\right) \, S_{\varXi }\nonumber \\&\times \left( E-\frac{\mathbf{p}^2}{2M_n}-\frac{\mathbf{q}^2}{2M_n},\mathbf{p+q}\right) \nonumber \\&\times \,{\mathscr {D}}_1\left( E-\frac{\mathbf{q}^2}{2M_n},\mathbf{q}\right) \nonumber \\&-\, {{\mathcal {C}}}^{(11)}_3(-y^2_1)\frac{M_{\varXi }}{2} \int ^{\varLambda _{\mathrm{reg}}} \frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3} t_A\left( \mathbf{q,k};E\right) {\mathscr {D}}_1\nonumber \\&\times \left( E-\frac{\mathbf{q}^2}{2M_n},\mathbf{q}\right) \frac{g_3(\varLambda _{\mathrm{reg}})}{\varLambda ^2_{\mathrm{reg}}} \nonumber \\&-\, {{\mathcal {C}}}^{(10)}_2 (-y_0y_1)\int ^{\varLambda _{\mathrm{reg}}} \frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3}\, t_B\left( \mathbf{q,k};E\right) S_n\nonumber \\&\times \left( E-\frac{\mathbf{p}^2}{2M_n}-\frac{\mathbf{q}^2}{2M_{\varXi }},\mathbf{p+q}\right) \nonumber \\&\times \,{\mathscr {D}}_0\left( E-\frac{\mathbf{q}^2}{2M_{\varXi }},\mathbf{q}\right) +\, {{\mathcal {C}}}^{(10)}_3 (-y_0y_1)\sqrt{\frac{3}{2}}M_n\nonumber \\&\times \,\int ^{\varLambda _{\mathrm{reg}}}\,\frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3}\, t_B\left( \mathbf{q,k};E\right) \frac{g_3(\varLambda _{\mathrm{reg}})}{\varLambda ^2_{\mathrm{reg}}} \nonumber \\&\times \,{\mathscr {D}}_0\left( E-\frac{\mathbf{q}^2}{2M_{\varXi }},\mathbf{q}\right) \,, \end{aligned}$$

(54)

and

$$\begin{aligned} t_B\left( \mathbf{p,k};E\right)= & {} (-y_0y_1)\left[ {{\mathcal {C}}}^{(10)}_2 S_n\left( E-\frac{\mathbf{k}^2}{2M_n}-\frac{\mathbf{p}^2}{2M_{\varXi }},\mathbf{p+k}\right) \right. \nonumber \\&\left. - {{\mathcal {C}}}^{(10)}_3 \sqrt{\frac{3}{2}}M_n\frac{g_3(\varLambda _{\mathrm{reg}})}{\varLambda ^2_{\mathrm{reg}}} \right] \nonumber \\&-\, {{\mathcal {C}}}^{(10)}_2(-y_0y_1) \int ^{\varLambda _{\mathrm{reg}}}\frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3} t_A\left( \mathbf{q,k};E\right) S_n\nonumber \\&\qquad \left( E-\frac{\mathbf{p}^2}{2M_{\varXi }}-\frac{\mathbf{q}^2}{2M_n},\mathbf{p+q}\right) \nonumber \\&\times \, {\mathscr {D}}_1\left( E-\frac{\mathbf{q}^2}{2M_n},\mathbf{q}\right) +\, {{\mathcal {C}}}^{(10)}_3 (-y_0y_1)\sqrt{\frac{3}{2}}M_n\nonumber \\&\times \,\int ^{\varLambda _{\mathrm{reg}}}\frac{\mathrm{d}^3\mathbf{q}}{(2\pi )^3}\, t_A\left( \mathbf{q,k};E\right) \frac{g_3(\varLambda _{\mathrm{reg}})}{\varLambda ^2_{\mathrm{reg}}} \nonumber \\&\times \,{\mathscr {D}}_1\left( E-\frac{\mathbf{q}^2}{2M_n},\mathbf{q}\right) \,. \end{aligned}$$

(55)

Here, ${{\mathcal {C}}}^{(11)}_2= 1/2$, ${{\mathcal {C}}}^{(10)}_2=-\sqrt{3/2}$ are spin–isospin re-coupling coefficients for diagrams with two-body interaction only, and ${{\mathcal {C}}}^{(11)}_3={{\mathcal {C}}}^{(10)}_3=1$ are those with the three-body contact interaction. Upon renormalization using the wavefunction renormalization constant ${\mathcal {Z}}_{\varXi n}$ (cf. Eq. (17)), and projecting on to the S-wave, the above amplitudes lead to Eqs. (13) and (14).