1 Introduction

Since the first proposals were made to use quantum effects for computing purposes there has been a strong focus on how errors and imperfections may harm and even prevent successful application of quantum computing. A simple estimate suggests that if each single operation in a computation entails an error with a probability then the application of k operations will lead to a useful outcome with a probability that decreases exponentially . Error correction codes have provided a way to correct these errors up to a certain probability threshold, thereby allowing scalable, fault-tolerant quantum computing [1, 2].

The errors occurring in a single computational step such as a one- or two-qubit gates are often characterized by a single number, typically related to the overlap between the desired and actual output state, averaged over all input states. There is no guarantee, however, that such a number encapsulates the accumulation of errors in a quantum circuit, where the output state of one operation serves as the input to the next. Errors may build up coherently, so that error probabilities grow quadratically rather than linearly with time, or so that they compensate each other, cf., bang-bang control and composite pulses [3–5]. Thus, a concatenation of two imperfect gates can lead to either unusable results or a correcting mechanism.

Consider the action of a quantum process that takes an input density matrix ρ describing a physical system with Hilbert space dimension D to an output density matrix. Such a process is described as a completely-positive linear map , where can be written [6]

(1)

by introducing a complete basis of operators on the Hilbert space. The coefficients constitute the process matrix χ.

In quantum computing we aim to implement definite gate operations yielding, ideally, a unitary transformation, . Expanding , this corresponds to Eq. (1) with . The process matrix of an experimental gate implementation differs from this form due to dissipation and decoherence. In this article, we will show that, provided dissipation and decoherence acts locally and is uncorrelated over the quantum computing register χ-matrices calculated once for one- and two-qubit gates can be concatenated, see Figure 1, to characterize circuits built from many of these gates. This assumption may be well justified in our example, which concerns neutral atom quantum computing, where the Rydberg blockade mechanism is used for two-qubit quantum gates [7, 8].

Figure 1
figure 1

Concatenation of gates carried out in parallel on different qubits (a), and in serial on the same qubits (b) in a quantum computer. Expressions for the resulting process matrices are discussed in Section 3.

Full size image

The paper is organized as follows. In Section 2, we review the definition of χ-matrices and how they may be computed with Monte Carlo wave function simulations. In Section 3, we describe how χ-matrices for simple processes on few particles are concatenated to characterize large quantum circuits. In Section 4, we introduce the Rydberg blockade gate scheme for quantum computing with neutral atoms. In Section 5, we concatenate one- and two-qubit gate χ-matrices in a neutral atom system to characterize the circuit performing a Toffoli gate. This we compare to a direct multi-atom Rydberg mediated implementation. In Section 6, we conclude and present an outlook.

2 Process matrix identification

Many techniques now exist to experimentally determine χ. Standard quantum process tomography [6, 9, 10] successfully reproduces χ by measuring all output states via quantum state tomography [11, 12]. This has been demonstrated in NMR [13, 14], optical [15, 16], and atomic systems [17]. Alternately, χ may be obtained making use of an ancillary system [18, 19] or avoiding state tomography altogether through the use of suitable ‘probe’ systems [20–22].

If the system is subject to known dissipation and decoherence mechanisms, the quantum system evolution may be modeled theoretically and the process matrix be calculated by solution of the quantum master equation. A gate operation typically involves application of time dependent laser pulses. Therefore, it is valuable to determine how losses and errors accumulate and contribute to different types of errors in the output. To theoretically characterize a complete quantum circuit is a formidable task and is ultimately at odds with using a physical system to solve computationally hard problems. Still, a theoretical analysis of how errors propagate and accumulate in small systems may guide efforts to pick among different implementations of gates and assess optimal strategies for error correction. Such detailed studies may also serve to confirm the values of experimental parameters [23, 24].

In a recent publication [25], we described how to characterize a quantum controlled-phase gate subject to decay and dephasing. Instead of simulating the evolution of a complete set of input states we gain access to all elements of χ by evolving a single maximally entangled pure state of the system and an idle ancilla system of the same Hilbert space dimension [18]. The system is propagated stochastically using the Monte Carlo wave function method, which on average reproduces results of a master equation evolution [26–28]. Process characterization using this approach has a number of advantages: First, for large D, an adequate ensemble of wave functions is easier to store and evolve than density matrices. Second, obtaining χ through the output state data from an ensemble of wave functions is less costly, numerically, than from a density matrix [25]. Third, the stochastic evolution consists of a deterministic smooth evolution interrupted by ‘quantum jumps’. Since useful quantum gates require excellent fidelity, jumps are rare and a single deterministic ‘no-jump’ wave function suffices to provide a good estimate and rigorous bound on the process matrices describing the evolution [25].

3 The process matrix for a quantum circuit

Suppose the quantum circuit performing a computational task is composed of N physical units. The Hilbert space of the entire system is then a tensor product of N Hilbert spaces, each of dimension d. An implementation of a quantum process often requires using more than just the qubit states. However, since the physical units only process binary information we shall refer to them as qubits, even if we exploit states from a space larger than dimension 2. On each qubit Hilbert space we assume the complete operator basis . By merely forming tensor products of the basis operators, we obtain a complete operator basis for the N qubits, where the single index n represents all values of the set . The operator tensor product structure provides a convenient representation of the operators () in Eq. (1).

If we assume that process matrices χ correctly describe processes acting separately on one and two qubits of the circuit, then the application of several one- and two-qubit operations is exactly represented by an appropriate concatenation of the corresponding process matrices.

3.1 Parallel concatenation

Suppose two subsystems are simultaneously subjected to processes independent of each other. These processes and may be described by the process matrices and respectively, illustrated as two- and one-qubit gates in Figure 1(a). The combined three-qubit process matrix is simply the tensor product of the independent χ matrices. Other systems may be present but idle during the gate operation. They are then represented by the identity operator in the process matrix tensor product.

3.2 Serial concatenation

Most quantum algorithms make use of many computational steps, where the output of every step serves as the input to the subsequent one. In Figure 1(b) we illustrate this situation for two consecutive three-qubit operations and characterized by and respectively. If the output of the input density matrix ρ becomes the input of , what is the resulting χ matrix? Formally, the output of the sequential application of the operations is given by

(2)

Since the operators form a complete set, any product can be expanded on these operators, that is, and . Equation (2) then becomes

(3)

where

(4)

Note that although two consecutive processes may act on different subsets of some multi-qubit system both operations may be reformulated to act on the entire system through parallel concatenation.

It now becomes apparent that once the process matrices of all contributing gates in a circuit have been computed conclusively, we limit the cost of finding and thus of process matrices for larger quantum circuits. The assessment of how errors accumulate becomes a function of the width and depth of the quantum circuit.

3.3 Example: Toffoli gate

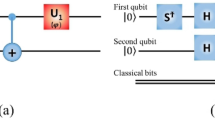
The Toffoli gate, or C2NOT gate, performs a controlled NOT operation on a target qubit based on the state of two control qubits. The Toffoli gate may be implemented as a sequence of six two-qubit C-NOT gates and nine one-qubit Hadamard and and phase gates, see Figure 2(a). The gate and its generalization to higher numbers of control qubits (C k -NOT) have applications as sub-modules in different quantum computing algorithms. Thus, it is relevant to determine the process matrix for its implementation in realistic systems.

Figure 2
figure 2

The Toffoli gate: (a) The three-qubit Toffoli gate on the left may be reproduced by a circuit of C-NOT, Hadamard (H), and gates, shown to the right. (b) The process matrix χ (left), characterizing the Toffoli gate may be calculated by concatenation of one- and two-qubit process matrices (right). The process matrices , , and characterize the C-NOT, Hadamard, T and gates respectively. The ‘identity’ process matrix indicates an idle qubit.

Full size image

In the analysis of the Toffoli gate process matrix we first simulated the propagation of quantum states in the full three-qubit Hilbert space through the sequence of one- and two-qubit gates. Such a calculation, e.g. using Monte Carlo wave functions to include dissipation, yields the full circuit process matrix . Next, we apply the concatenation rules to obtain the circuit’s process matrix . Its repeated use of the same C-NOT χ matrix (cf. Figure 2(b)), which only needs a single calculation on a two-qubit system, attests to the advantage of the latter approach.

4 Rydberg blockade quantum gates

A promising candidate for quantum computing involves neutral atoms held at closely spaced sites in far-off-resonance optical traps. The atoms may be individually addressed with laser fields and excited into high lying Rydberg states that feature strong, long distance dipole and van der Waals forces that can be used to mediate two-qubit interactions [7, 8, 29].

In Rubidium atoms, a convenient choice for the qubit states are the hyperfine ground states and . They can be selectively excited to the Rydberg state by a two photon process using a 780-nm (480-nm) laser field, tuned by an amount Δ to the red (blue) of the intermediate state. The Rabi frequency associated with the red (blue) detuned laser is (), illustrated in Figure 3(a). An atom that achieves excitation to the Rydberg state shifts the state energy of all other atoms within the so-called blockade radius by an amount ℬ. Thus, one excited atom can prevent the resonant excitation of its neighboring atoms and this is the basis for effective quantum gates between them.

Figure 3
figure 3

Simulation and characterization of the C-NOT gate: (a) The red (lower) and blue (upper) laser fields drive , via , into the Rydberg state by two-photon absorption. (b) Implementation of the C-NOT gate involves a sequence of two-photon π-pulses: In pulse 1 the control atom makes the transition to . The target atom then makes the transitions (pulse 2), (pulse 3) and finally (pulse 4). In pulses 2-4 the target atom’s states and are swapped, but only if the control atom is not in . Finally, in pulse 5 the control atom is driven from back to . (c) Trace distance (see text in Section 4.1) between the ideal C-NOT process matrix and the process matrix calculated for the implementation shown in panel (b), with the parameters listed in Table 1. The trace distance is shown as a function of the blue laser Rabi frequency .

Full size image

Dephasing of the Rydberg level normally associated with magnetic field noise and atomic motion is modeled by the operator , where is the dephasing rate and is shorthand for the identity operator. Spontaneous decay from a state to a lower lying state at a rate is modeled by the jump operator . The effects of both dissipation mechanisms are simulated using the Monte Carlo wave function method [25]. Characteristic parameters are summarized in Table 1.

Table 1 Physical parameters for our simulations based on values discussed in Refs. [30, 31]
Full size table

Adiabatic elimination by the effective operator formalism detailed in Ref. [32] provides a mechanism to decouple the intermediate optically excited state and describe the coherent and incoherent dynamics within the subspace of and . The system is then described by a Hamiltonian coupling a selected qubit state to by an effective Rabi frequency. The formalism also provides an effective form for the operators describing decohering processes [25].

4.1 Rydberg blockade C-NOT gate

In atomic quantum computing proposals, single qubit gates amount to fast, resonant transitions within single atoms and can be made with high precision. Thus, for the purpose of this study we assume that the χ matrices associated with one-qubit gates are identical to the desired ones. The two-qubit C-NOT gate depends on finite interactions between excited state atoms, lengthening gate time and making it prone to dissipation and decoherence.

Figure 3(b) illustrates how a unitary C-NOT gate between two atoms can be implemented by a sequence of five perfect π-pulses. First transferring the control qubit’s population from to (pulse 1), then transferring the target qubit’s population between and via the state (pulses 2-4) and finally returning the control qubit’s population from to (pulse 5). If the control qubit initially populates the state the Rydberg blockade prevents any transfer during pulses 2-4. Thus, a NOT operation on the target qubit is conditioned on the control qubit initially populating the state , defining it to be a C-NOT operation.

Monte Carlo wave functions were used to simulate the five π-pulse implementation of the C-NOT gate (Figure 3) with the parameters of Table 1. The performance of the gate was investigated as a function of the blue laser Rabi frequency . To provide a simple quantitative measure we applied the trace distance measure between the simulated and ideal process matrix, where and is the trace norm. Note that this distance measure is less ‘forgiving’ than, for example, measures based on the trace overlap [23]. In Figure 3(c) we show the trace distance between a simulated C-NOT gate process matrix and the ideal, unitary process matrix. At low values of the gate experiences greater dephasing errors from population in the Rydberg state, due to long gate times. At large the blockade mechanism becomes inefficient. Thus, the optimum Rabi frequency lies between these two regimes.

5 The Toffoli gate by Rydberg blockade

We demonstrate the characterization of the Toffoli gate resulting from simulation in Figure 4. The process matrix of the Toffoli gate in the circuit implementation (Figure 2) may be obtained without further simulation by a concatenation of the single qubit process matrices and the C-NOT process matrix of Section 4.1. Alternatively, we may simulate the circuit implementation in the full three-qubit Hilbert space to obtain . In the simulation of a Rydberg mediated gate, the characterization of a single qubit has a Hilbert space dimension of , which translates into a 46 problem for the three qubit circuit characterization. We observe that the Toffoli gate consists of six C-NOT gates and the trace distance to the ideal gate is, indeed, roughly six times the one shown in Figure 3(c).

Figure 4
figure 4

Trace distance between the process matrix for the ideal Toffoli gate and the process matrices for Rydberg interaction implementations subject to dissipation and decoherence. The results are shown as a function of the Rabi frequency of the (blue) laser coupling. The dashed curve is obtained by simulating all three qubits as they evolve under the sequence of gates in the Toffoli circuit shown in Figure 2(a). The top solid curve uses concatenation of the one- and two-qubit process matrices to compute the Toffoli circuit process matrix. The bottom (solid) curve results from simulating the multi-qubit implementation shown in Figure 5. In all calculations 500 Monte Carlo trajectories were used with the parameters listed in Table 1.

Full size image

The top dashed (solid) curve in Figure 4 illustrates trace distance between the full circuit (concatenated ) process matrix to the ideal process matrix , plotted as a function of . Since the decay and decoherence processes apply to the individual atoms, the successive treatment of the evolution of the atoms acted upon by the laser fields and concatenation of the resulting one- and two-qubit process matrices should yield the same results as the solution on the full-register Hilbert space.

Each point in both curves is determined by propagating wave function trajectories, and the minor discrepancy between the two curves is due to the use of the MCWF method. The final number of propagated wave functions imposes a statistical error on both curves. Furthermore, it imposes a small systematical error in the construction of , because the same simulated C-NOT process matrix is applied several times to form the concatenated process matrix (see Ref. [33] for an analysis of a similar situation). The discrepancy between the curves in Figure 4 depends on . For low values of , and thus slow gate operation, decay and dephasing dominate the error. More random quantum jumps occur and the resulting scattering of Monte Carlo wave functions explains the relatively large discrepancy between and . For high values of , imperfect blockade dominates the gate error. This corresponds to a unitary term in the state evolution which is well represented by a single wave function, and the discrepancy between and decreases for large .

A Rydberg excited atom blocks excitation of any number of atoms within the Rydberg interaction blockade radius, which may be of order 10 μm. Thus, it is possible to contain an entire qubit register within a single blockade radius, allowing implementation of multi-qubit gate operations which are faster than the circuit equivalent [34]. One such protocol is the C k NOT gate operation, illustrated in Figure 5 [35].

Figure 5
figure 5

Multi-qubit Rydberg blockade implementation of a NOT gate. Each control atom is sequentially excited from to in k π-pulses. Next, the target atom qubit states are swapped as in Figure 3(b), via the Rydberg state (conditioned on no control atom populating the state ). The control atoms are then returned to their original state in reverse order. The trace distance between the process matrix using this implementation for and the ideal Toffoli gate is shown as the lower curve in Figure 4.

Full size image

For the gate becomes the Toffoli gate and calculation of the process matrix is only possible by solving the master equation for the complete qubit register. In this paper, simulation of the process, including the decay and decoherence mechanisms detailed above, was carried out using the Monte Carlo method. The trace distance between the process matrix resulting from simulation and the ideal process matrix is shown as the lower, black curve in Figure 4. Remarkably, the multi-qubit implementation, with interactions allowed between all three atoms, performs markedly better than the Toffoli circuit consisting of one- and two-qubit operations. In comparison with the C-NOT gate, the minimal trace distance here is approximately 1.5 times larger. This is consistent with using 7 π-pulses rather than the 5 needed for a single C-NOT gate.

6 Conclusion

In conclusion, we have presented an efficient method to compute the accumulation of errors in quantum circuits comprised of several few-qubit gates. We have shown that a set of concatenation rules on the appropriate few-qubit gate process matrices is enough to reproduce the process matrix of the entire circuit. To demonstrate the method’s efficiency at calculating process matrices of large systems we considered the three-qubit Toffoli gate. The Toffoli gate may be implemented as a circuit of one- and two-qubit gates and simulations show that the process matrix obtained via concatenation is in good agreement with the result achieved by propagation through the entire circuit.

Our theory allows comparison of different implementations of gates. In particular, we compared a multi-qubit implementation of the Toffoli gate with its one- and two-qubit circuit implementation. For the parameters chosen, the factor determining gate fidelity was the number of laser π-pulses. More gates lead to a lower fidelity, with a dependence that is almost linear. In this way, our analysis provides the necessary information to choose between different gate implementations. A theory of full error correction may benefit significantly from knowledge of the precise nature of errors incurred, potentially leading to higher thresholds for errors that can be remedied by appropriate error correction. The full process matrix, which remains at our disposal, may be further applied to optimally combine the Toffoli gate with previous and subsequent gate operations along the lines of NMR composite pulses [4].

Our analysis quantifies how erroneous states prepared by one gate are the input states to the subsequent ones and how the resulting accumulation of errors cause the full register quantum state to stray away from the ideal unitary evolution. The calculations assumed a quantum optical master equation with independent Lindblad type relaxation terms. This is well justified for Rydberg blockade quantum computing with optical excitation of neutral atoms, but it also applies for a number of quantum computing proposals with similarly isolated and identifiable qubits. However, if the deleterious interaction between the quantum register and its environment is subject to correlations between qubits and non-Markovian effects, more care must be exercised in the assessment of how errors accumulate, and how they may be corrected [36, 37].